2022人教版 九年级 数学下册 28.2 解直角三角形及其应用( 第1课时) 课件(共33张PPT)
文档属性
| 名称 | 2022人教版 九年级 数学下册 28.2 解直角三角形及其应用( 第1课时) 课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 11:19:53 | ||
图片预览






文档简介
(共33张PPT)
28.2.2 应用举例
第1课时
识新知·自主预习
【旧知再现】
1.由直角三角形中的_____________,求出_________________的过程,叫做
解直角三角形.
2.解直角三角形基本类型:(1)已知_________求其他未知元素;
(2)已知_____________求其他未知元素.
已知元素
其余未知元素
两边
一边一角
【新知初探】
阅读教材P74-75内容,解决以下问题:
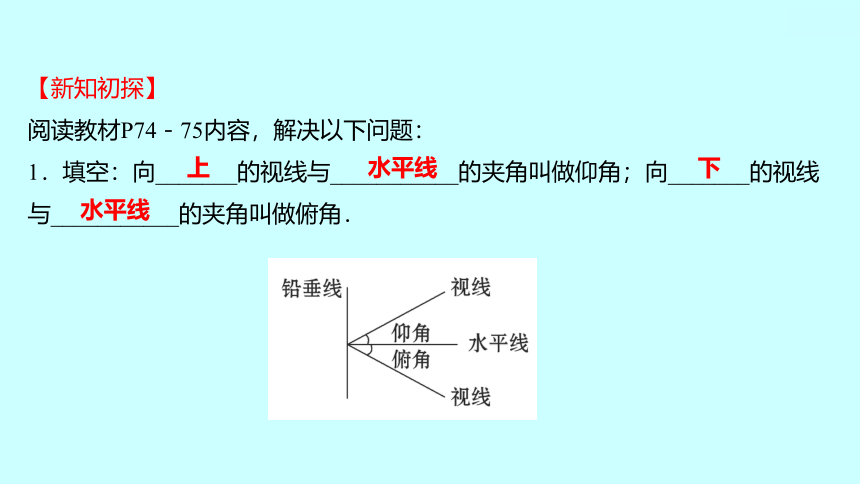
1.填空:向_______的视线与___________的夹角叫做仰角;向_______的视线
与___________的夹角叫做俯角.
上
水平线
下
水平线
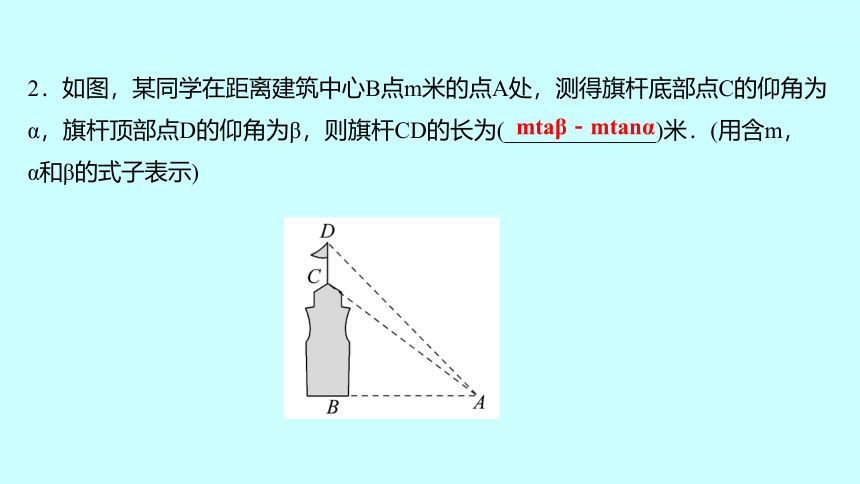
2.如图,某同学在距离建筑中心B点m米的点A处,测得旗杆底部点C的仰角为
α,旗杆顶部点D的仰角为β,则旗杆CD的长为(_____________)米.(用含m,
α和β的式子表示)
mtaβ-mtanα
3.总结:利用解直角三角形解决实际问题的步骤
(1)把实际问题建立_____________.
(2)根据已知条件,选用适当的_________函数解直角三角形.
(3)得到_________问题的答案.
(4)得到_________问题的答案.
数学模型
三角
数学
实际
【图表导思】
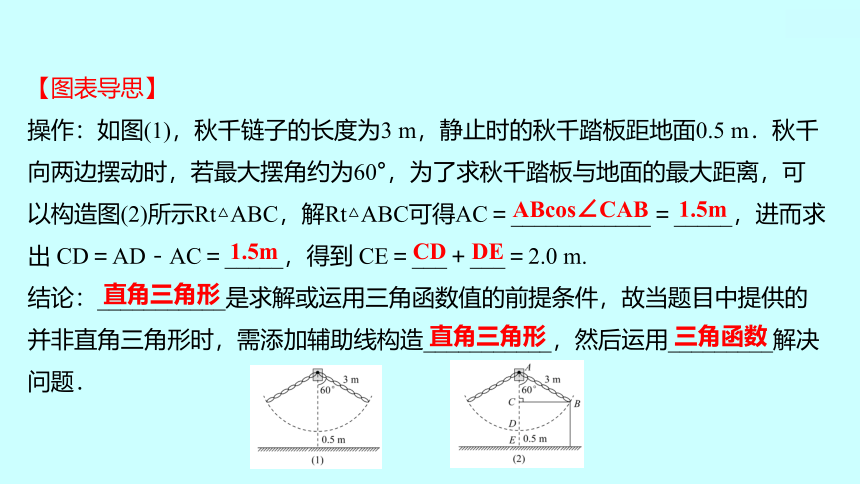
操作:如图(1),秋千链子的长度为3 m,静止时的秋千踏板距地面0.5 m.秋千
向两边摆动时,若最大摆角约为60°,为了求秋千踏板与地面的最大距离,可
以构造图(2)所示Rt△ABC,解Rt△ABC可得AC=____________=_____,进而求
出 CD=AD-AC=_____,得到 CE=___+___=2.0 m.
结论:___________是求解或运用三角函数值的前提条件,故当题目中提供的
并非直角三角形时,需添加辅助线构造___________,然后运用_________解决
问题.
ABcos∠CAB
1.5m
1.5m
CD
DE
直角三角形
直角三角形
三角函数
【妙招巧记】
视线水平线,
夹角分仰俯;
视线水平上,
夹角为仰角;
视线水平下,
夹角为俯角.
研重点·典例探析
知识点一 解直角三角形的简单应用
【教材P74例3补充】——构造直角三角形解决简单的实际问题
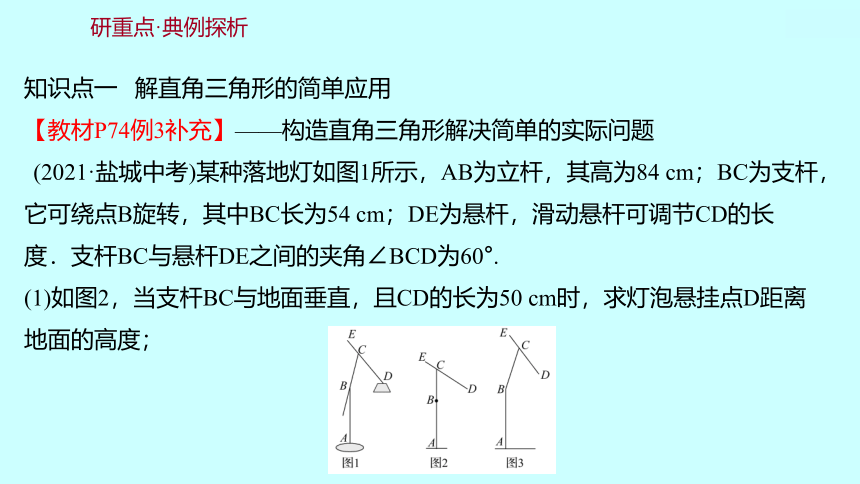
(2021·盐城中考)某种落地灯如图1所示,AB为立杆,其高为84 cm;BC为支杆,它可绕点B旋转,其中BC长为54 cm;DE为悬杆,滑动悬杆可调节CD的长度.支杆BC与悬杆DE之间的夹角∠BCD为60°.
(1)如图2,当支杆BC与地面垂直,且CD的长为50 cm时,求灯泡悬挂点D距离地面的高度;
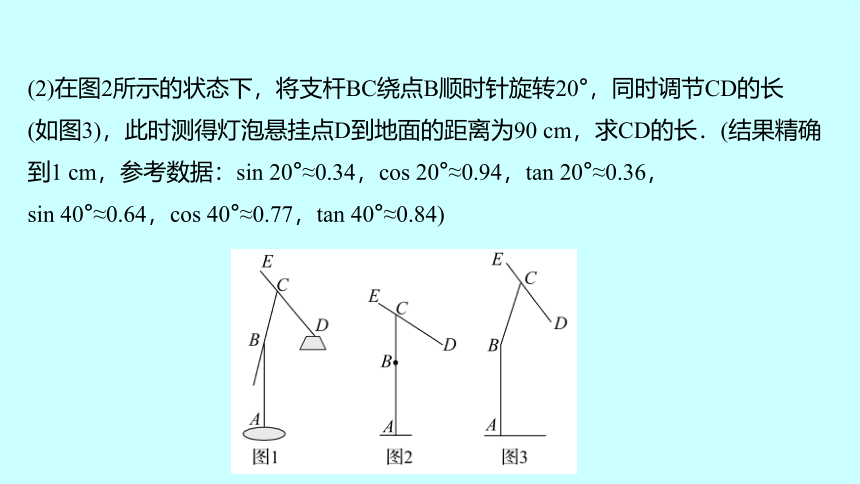
(2)在图2所示的状态下,将支杆BC绕点B顺时针旋转20°,同时调节CD的长
(如图3),此时测得灯泡悬挂点D到地面的距离为90 cm,求CD的长.(结果精确
到1 cm,参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36,
sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
【完善解答】(1)过点D作DF⊥_______于F,……作垂线构造直角三角形
∵∠FCD=60°,∠CFD=90°,
∴FC=CD×__________=50× =_______(cm),……利用余弦求出FC的长
∴FA=AB+BC-_______=84+54-_______=________(cm),
………………………………………………根据线段的和差求出FA的长
答:灯泡悬挂点D距离地面的高度为________ cm;
………………………………………………………………写出实际问题的答案
BC
cos60°
25
CF
25
113
113
(2)如图3,过点C作CG垂直于地面于点G,过点B作BN⊥________于N,过点
D作DM⊥________于M,………………………………作垂线构造直角三角形
∵BC=54 cm,
∴CN=BC× ______≈54×____=_____(cm),…………利用余弦求出CN的长
∴MN=CN+________-CG=_________+_______-50.76-_______=______(cm),………………………根据线段的和差求出MN的长
∴CM=CN-____=_____(cm),…根据线段的和差求出CM的长
∴CD=_______________≈58(cm),…………利用余弦求出CD的长
答:CD的长为_______ cm.………………写出实际问题的答案
CG
CG
cos20°
0.94
50.76
MG
50.76
90
84
6
MN
44.76
58
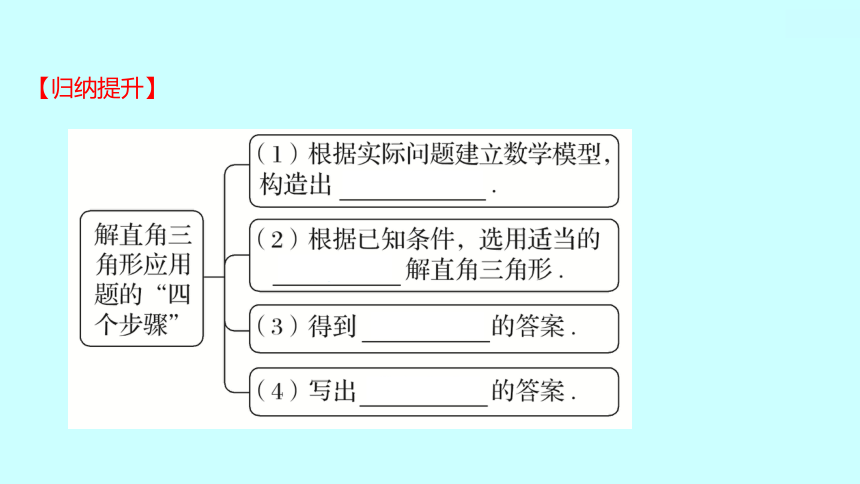
【归纳提升】
A
培素养·思维拓展
利用解直角三角形解决实际问题
仰角
俯角
步骤
选用适当的三角函数解直角三角形.
建立数学模型
得到数学问题的答案
得到实际问题的答案
解答仰角俯角问题的三点注意
28.2.2 应用举例
第1课时
识新知·自主预习
【旧知再现】
1.由直角三角形中的_____________,求出_________________的过程,叫做
解直角三角形.
2.解直角三角形基本类型:(1)已知_________求其他未知元素;
(2)已知_____________求其他未知元素.
已知元素
其余未知元素
两边
一边一角
【新知初探】
阅读教材P74-75内容,解决以下问题:
1.填空:向_______的视线与___________的夹角叫做仰角;向_______的视线
与___________的夹角叫做俯角.
上
水平线
下
水平线
2.如图,某同学在距离建筑中心B点m米的点A处,测得旗杆底部点C的仰角为
α,旗杆顶部点D的仰角为β,则旗杆CD的长为(_____________)米.(用含m,
α和β的式子表示)
mtaβ-mtanα
3.总结:利用解直角三角形解决实际问题的步骤
(1)把实际问题建立_____________.
(2)根据已知条件,选用适当的_________函数解直角三角形.
(3)得到_________问题的答案.
(4)得到_________问题的答案.
数学模型
三角
数学
实际
【图表导思】
操作:如图(1),秋千链子的长度为3 m,静止时的秋千踏板距地面0.5 m.秋千
向两边摆动时,若最大摆角约为60°,为了求秋千踏板与地面的最大距离,可
以构造图(2)所示Rt△ABC,解Rt△ABC可得AC=____________=_____,进而求
出 CD=AD-AC=_____,得到 CE=___+___=2.0 m.
结论:___________是求解或运用三角函数值的前提条件,故当题目中提供的
并非直角三角形时,需添加辅助线构造___________,然后运用_________解决
问题.
ABcos∠CAB
1.5m
1.5m
CD
DE
直角三角形
直角三角形
三角函数
【妙招巧记】
视线水平线,
夹角分仰俯;
视线水平上,
夹角为仰角;
视线水平下,
夹角为俯角.
研重点·典例探析
知识点一 解直角三角形的简单应用
【教材P74例3补充】——构造直角三角形解决简单的实际问题
(2021·盐城中考)某种落地灯如图1所示,AB为立杆,其高为84 cm;BC为支杆,它可绕点B旋转,其中BC长为54 cm;DE为悬杆,滑动悬杆可调节CD的长度.支杆BC与悬杆DE之间的夹角∠BCD为60°.
(1)如图2,当支杆BC与地面垂直,且CD的长为50 cm时,求灯泡悬挂点D距离地面的高度;
(2)在图2所示的状态下,将支杆BC绕点B顺时针旋转20°,同时调节CD的长
(如图3),此时测得灯泡悬挂点D到地面的距离为90 cm,求CD的长.(结果精确
到1 cm,参考数据:sin 20°≈0.34,cos 20°≈0.94,tan 20°≈0.36,
sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)
【完善解答】(1)过点D作DF⊥_______于F,……作垂线构造直角三角形
∵∠FCD=60°,∠CFD=90°,
∴FC=CD×__________=50× =_______(cm),……利用余弦求出FC的长
∴FA=AB+BC-_______=84+54-_______=________(cm),
………………………………………………根据线段的和差求出FA的长
答:灯泡悬挂点D距离地面的高度为________ cm;
………………………………………………………………写出实际问题的答案
BC
cos60°
25
CF
25
113
113
(2)如图3,过点C作CG垂直于地面于点G,过点B作BN⊥________于N,过点
D作DM⊥________于M,………………………………作垂线构造直角三角形
∵BC=54 cm,
∴CN=BC× ______≈54×____=_____(cm),…………利用余弦求出CN的长
∴MN=CN+________-CG=_________+_______-50.76-_______=______(cm),………………………根据线段的和差求出MN的长
∴CM=CN-____=_____(cm),…根据线段的和差求出CM的长
∴CD=_______________≈58(cm),…………利用余弦求出CD的长
答:CD的长为_______ cm.………………写出实际问题的答案
CG
CG
cos20°
0.94
50.76
MG
50.76
90
84
6
MN
44.76
58
【归纳提升】
A
培素养·思维拓展
利用解直角三角形解决实际问题
仰角
俯角
步骤
选用适当的三角函数解直角三角形.
建立数学模型
得到数学问题的答案
得到实际问题的答案
解答仰角俯角问题的三点注意
