2022人教版九年级数学下册28.2 解直角三角形及其应用( 第2课时 )课件 (共29张PPT)
文档属性
| 名称 | 2022人教版九年级数学下册28.2 解直角三角形及其应用( 第2课时 )课件 (共29张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 00:00:00 | ||
图片预览





文档简介
(共29张PPT)
28.2.2应 用 举 例
第2课时
识新知·自主预习
【旧知再现】
1.在视线与水平线所成的角中,视线在水平线上方的叫做_________,视线在
水平线下方的叫做_________.
2.利用解直角三角形解决仰(俯)角问题的步骤要点:(1)根据实际问题情境构造
_______________;(2)选择适当的三角函数解_______________;(3)根据数学问
题的答案写出___________________.
仰角
俯角
直角三角形
直角三角形
实际问题的答案
【新知初探】
阅读教材P76-77内容,解决以下问题:
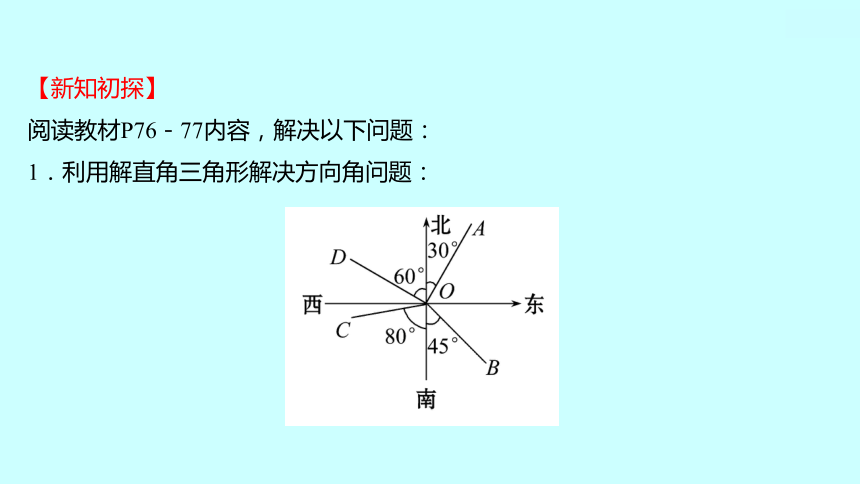
1.利用解直角三角形解决方向角问题:
(1)探究:
如图中的目标方向线OA,OB,OC,OD的方向角分别表示为_____________,
_____________,_____________,_____________.
(2)结论:
指_____或指_____方向线与目标方向线所成的小于_____的角叫做方向角.
北偏东30°
东南方向
南偏西80°
北偏西60°
北
南
90°
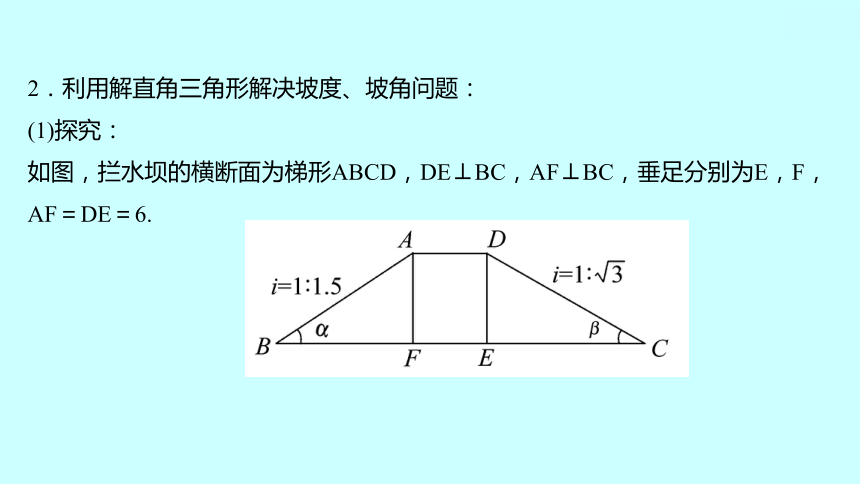
2.利用解直角三角形解决坡度、坡角问题:
(1)探究:
如图,拦水坝的横断面为梯形ABCD,DE⊥BC,AF⊥BC,垂足分别为E,F,AF=DE=6.
①坡度i=1∶1.5表示_______________,
坡度i=1∶ 表示_____________.
②tan α=____,则α≈__________;tan β=____,β=_______.
③因为AF=6,所以BF=______,AB=______.
④因为DE=6,所以CE=____,CD=_______.
AF∶BF=1∶1.5
33.69°
30°
9
12
(2)结论:
坡度:坡面的_____________h和_____________l的比叫做坡度(或叫做坡比),
一般用i表示.即i= ,常写成i=1∶m的形式.
坡角:把坡面与水平面的夹角α叫做坡角.
铅直高度
水平宽度
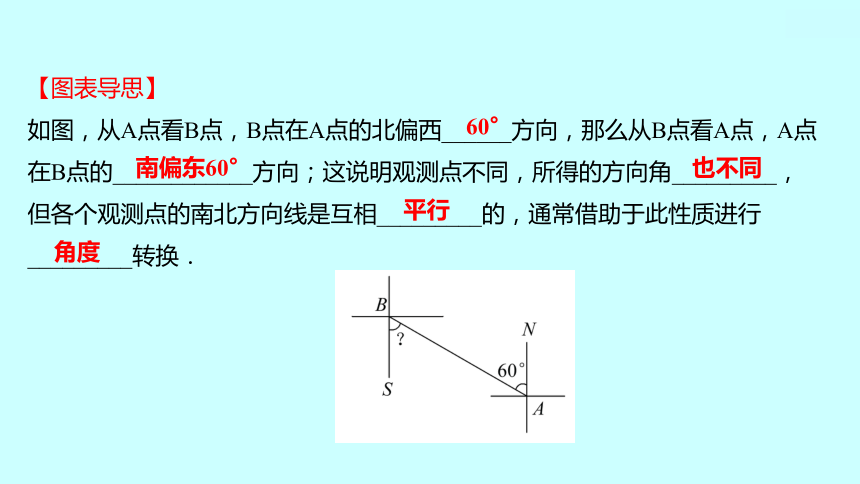
【图表导思】
如图,从A点看B点,B点在A点的北偏西______方向,那么从B点看A点,A点
在B点的____________方向;这说明观测点不同,所得的方向角_________,
但各个观测点的南北方向线是互相_________的,通常借助于此性质进行
_________转换.
60°
南偏东60°
也不同
平行
角度
【妙招巧记】
方向角的两条边,
一定要有南北线;
书写讲究要规范,
先说南北再东西.
【质疑判断】
(1)坡角就是坡面与地面的夹角.( )
(2)坡度就是坡角的度数.( )
(3)坡度等于坡角的正切值.( )
(4)坡度越大,坡角越大,坡面越陡.( )
×
×
√
√
研重点·典例探析
【思维模板】
通关四步 具体操作
理解题意 已知不规则四边形相互垂直的两边的长度以及各角度数,求直角对面的顶点到直角边的距离.
思路探索 过点D作DE⊥AB于E,过D作DF⊥BC于F,则四边形EBFD是矩形,设DE=x,根据BE=DF=CF,列方程可得结果.
【归纳提升】
变式一:巩固
(2021·武汉中考)如图,海中有一个小岛A,一艘轮船由西向东航行,在B点测得
小岛A在北偏东60°方向上;航行12 nmile到达C点,这时测得小岛A在北偏东30°
方向上.小岛A到航线BC的距离是_____________( ≈1.73,结果用四舍五入
法精确到0.1).
10.4 nmile
应用解直角三角形解决坡度、坡角问题
【教材P77练习T2拓展】——构造直角三角形解决坡度、坡角问题
(2021·扬州模拟)时代购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的坡度为1∶3,一楼到地下停车场地面的垂直高度CD=3.2 m,一楼到地平线的距离BC=1 m.
(1)为保证斜坡的坡度为1∶3,应在地面上距点B多远的A处开始斜坡的施工?
(2)如果给该购物广场送货的货车高度为2.8 m,那么按这样的设计能否保证货车顺利进入地下停车场?并说明理由.(参考数据: ≈3.2)
【归纳提升】
变式一:巩固 (2021·山西中考)太原地铁2号线是山西省第一条开通运营的地铁
线路,于2020年12月26日开通,如图是该地铁某站扶梯的示意图,扶梯AB的
坡度i=5∶12(i为铅直高度与水平宽度的比).王老师乘扶梯从扶梯底端A以0.5米/
秒的速度用时40秒到达扶梯顶端B,则王老师上升的铅直高度BC为____米.
变式二:提升 汛期即将来临,为保证市民的生命和财产安全,市政府决定对一
段长200米且横断面为梯形的大坝用土石进行加固.如图,加固前大坝背水坡
坡面从A至B共有30级阶梯,平均每级阶梯高30 cm,斜坡AB的坡度i=1∶1;
加固后,坝顶宽度增加2米,斜坡EF的坡度i=1∶ ,问工程完工后,共需土
石多少立方米?(计算土石方时忽略阶梯,结果保留根号)
【完善解答】过A 作AH⊥_______于H,过E作EG⊥_______于G,……………
作垂线构造直角则四边形EGHA是矩形,
∴EG=________,GH=_______=2, …………………………
矩形的判定与性质
∵斜坡AB的坡度i=1∶1,
∴AH=_______=__________cm=________cm=______米, ……………
坡度的意义
∴BG=BH-________=______,
BC
BC
AH
AE
BH
30×30
900
9
HG
7
∵斜坡EF的坡度i=1∶ ,
∴FG=______=____, …………………………坡度的意义
∴BF=FG-_______=________, …………………………线段的和差
∴S梯形ABFE= = , …………………………
梯形面积
∴共需土石为:_____________×200=_____________立方米. ……………
计算结果
BG
培素养·思维拓展
利用解直角三角形解决实际问题
方向角
问题
坡度坡角问题
由实际问题转化为数学图形
正确标注方向角
坡角:把坡面与水平面的夹角α叫做坡角.
坡度:坡面的铅直高度h和水平宽度l的比叫做坡度
1.明确坡度概念 2.坡度越大,坡角也越大 3.构造直角三角形和矩形来求解
注意
28.2.2应 用 举 例
第2课时
识新知·自主预习
【旧知再现】
1.在视线与水平线所成的角中,视线在水平线上方的叫做_________,视线在
水平线下方的叫做_________.
2.利用解直角三角形解决仰(俯)角问题的步骤要点:(1)根据实际问题情境构造
_______________;(2)选择适当的三角函数解_______________;(3)根据数学问
题的答案写出___________________.
仰角
俯角
直角三角形
直角三角形
实际问题的答案
【新知初探】
阅读教材P76-77内容,解决以下问题:
1.利用解直角三角形解决方向角问题:
(1)探究:
如图中的目标方向线OA,OB,OC,OD的方向角分别表示为_____________,
_____________,_____________,_____________.
(2)结论:
指_____或指_____方向线与目标方向线所成的小于_____的角叫做方向角.
北偏东30°
东南方向
南偏西80°
北偏西60°
北
南
90°
2.利用解直角三角形解决坡度、坡角问题:
(1)探究:
如图,拦水坝的横断面为梯形ABCD,DE⊥BC,AF⊥BC,垂足分别为E,F,AF=DE=6.
①坡度i=1∶1.5表示_______________,
坡度i=1∶ 表示_____________.
②tan α=____,则α≈__________;tan β=____,β=_______.
③因为AF=6,所以BF=______,AB=______.
④因为DE=6,所以CE=____,CD=_______.
AF∶BF=1∶1.5
33.69°
30°
9
12
(2)结论:
坡度:坡面的_____________h和_____________l的比叫做坡度(或叫做坡比),
一般用i表示.即i= ,常写成i=1∶m的形式.
坡角:把坡面与水平面的夹角α叫做坡角.
铅直高度
水平宽度
【图表导思】
如图,从A点看B点,B点在A点的北偏西______方向,那么从B点看A点,A点
在B点的____________方向;这说明观测点不同,所得的方向角_________,
但各个观测点的南北方向线是互相_________的,通常借助于此性质进行
_________转换.
60°
南偏东60°
也不同
平行
角度
【妙招巧记】
方向角的两条边,
一定要有南北线;
书写讲究要规范,
先说南北再东西.
【质疑判断】
(1)坡角就是坡面与地面的夹角.( )
(2)坡度就是坡角的度数.( )
(3)坡度等于坡角的正切值.( )
(4)坡度越大,坡角越大,坡面越陡.( )
×
×
√
√
研重点·典例探析
【思维模板】
通关四步 具体操作
理解题意 已知不规则四边形相互垂直的两边的长度以及各角度数,求直角对面的顶点到直角边的距离.
思路探索 过点D作DE⊥AB于E,过D作DF⊥BC于F,则四边形EBFD是矩形,设DE=x,根据BE=DF=CF,列方程可得结果.
【归纳提升】
变式一:巩固
(2021·武汉中考)如图,海中有一个小岛A,一艘轮船由西向东航行,在B点测得
小岛A在北偏东60°方向上;航行12 nmile到达C点,这时测得小岛A在北偏东30°
方向上.小岛A到航线BC的距离是_____________( ≈1.73,结果用四舍五入
法精确到0.1).
10.4 nmile
应用解直角三角形解决坡度、坡角问题
【教材P77练习T2拓展】——构造直角三角形解决坡度、坡角问题
(2021·扬州模拟)时代购物广场要修建一个地下停车场,停车场的入口设计示意图如图所示,其中斜坡的坡度为1∶3,一楼到地下停车场地面的垂直高度CD=3.2 m,一楼到地平线的距离BC=1 m.
(1)为保证斜坡的坡度为1∶3,应在地面上距点B多远的A处开始斜坡的施工?
(2)如果给该购物广场送货的货车高度为2.8 m,那么按这样的设计能否保证货车顺利进入地下停车场?并说明理由.(参考数据: ≈3.2)
【归纳提升】
变式一:巩固 (2021·山西中考)太原地铁2号线是山西省第一条开通运营的地铁
线路,于2020年12月26日开通,如图是该地铁某站扶梯的示意图,扶梯AB的
坡度i=5∶12(i为铅直高度与水平宽度的比).王老师乘扶梯从扶梯底端A以0.5米/
秒的速度用时40秒到达扶梯顶端B,则王老师上升的铅直高度BC为____米.
变式二:提升 汛期即将来临,为保证市民的生命和财产安全,市政府决定对一
段长200米且横断面为梯形的大坝用土石进行加固.如图,加固前大坝背水坡
坡面从A至B共有30级阶梯,平均每级阶梯高30 cm,斜坡AB的坡度i=1∶1;
加固后,坝顶宽度增加2米,斜坡EF的坡度i=1∶ ,问工程完工后,共需土
石多少立方米?(计算土石方时忽略阶梯,结果保留根号)
【完善解答】过A 作AH⊥_______于H,过E作EG⊥_______于G,……………
作垂线构造直角则四边形EGHA是矩形,
∴EG=________,GH=_______=2, …………………………
矩形的判定与性质
∵斜坡AB的坡度i=1∶1,
∴AH=_______=__________cm=________cm=______米, ……………
坡度的意义
∴BG=BH-________=______,
BC
BC
AH
AE
BH
30×30
900
9
HG
7
∵斜坡EF的坡度i=1∶ ,
∴FG=______=____, …………………………坡度的意义
∴BF=FG-_______=________, …………………………线段的和差
∴S梯形ABFE= = , …………………………
梯形面积
∴共需土石为:_____________×200=_____________立方米. ……………
计算结果
BG
培素养·思维拓展
利用解直角三角形解决实际问题
方向角
问题
坡度坡角问题
由实际问题转化为数学图形
正确标注方向角
坡角:把坡面与水平面的夹角α叫做坡角.
坡度:坡面的铅直高度h和水平宽度l的比叫做坡度
1.明确坡度概念 2.坡度越大,坡角也越大 3.构造直角三角形和矩形来求解
注意
