2022人教版数学九年级下册 27.2.3.2相似三角形应用举例课件(可编辑图片版、共20张PPT)
文档属性
| 名称 | 2022人教版数学九年级下册 27.2.3.2相似三角形应用举例课件(可编辑图片版、共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 587.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 13:31:20 | ||
图片预览





文档简介
(共20张PPT)
27.2.3相似三角形应用举例
第2课时
识新知·自主预习
【旧知再现】
1.利用_________________等工具,通过构造相似三角形,可以测量树高、
河宽等.
2.应用相似三角形进行测量时,一般要用到相似三角形对应边___________
和对应高的比等于___________.
标杆、反光镜
成比例
相似比
【新知初探】
进一步深入研讨教材P39-41,归纳有关结论
应用相似三角形进行测量的一般步骤
(1)利用平行线、标杆等构成_________三角形.
(2)测量与表示未知量的线段相对应的线段的长,以及另外任意一组对应边的
长度.
(3)画出示意图,利用相似三角形的性质,列出以上包括未知量在内的四个量
的___________,解出未知量.
(4)检验并得出答案.
相似
比例式
【妙招巧记】
相似测量分四步:
一构相似三角形,
二测有关线段长,
三是列出比例式,
四解方程写答案.
【质疑判断】
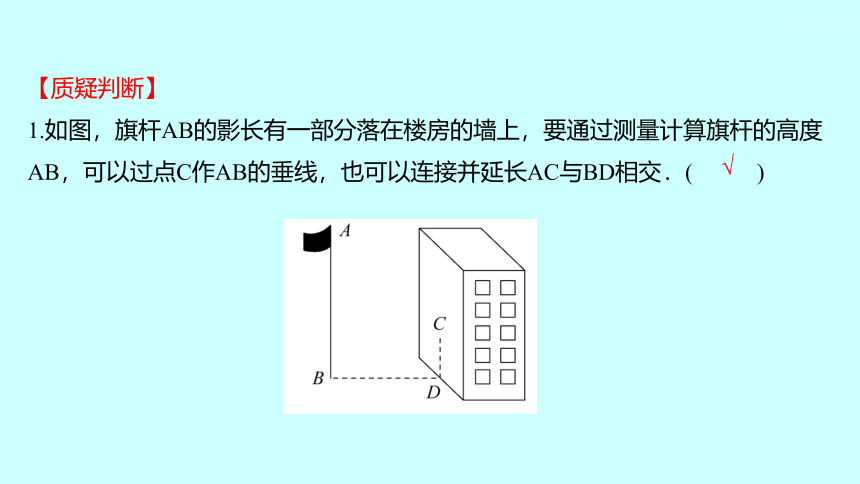
1.如图,旗杆AB的影长有一部分落在楼房的墙上,要通过测量计算旗杆的高度
AB,可以过点C作AB的垂线,也可以连接并延长AC与BD相交.( )
√
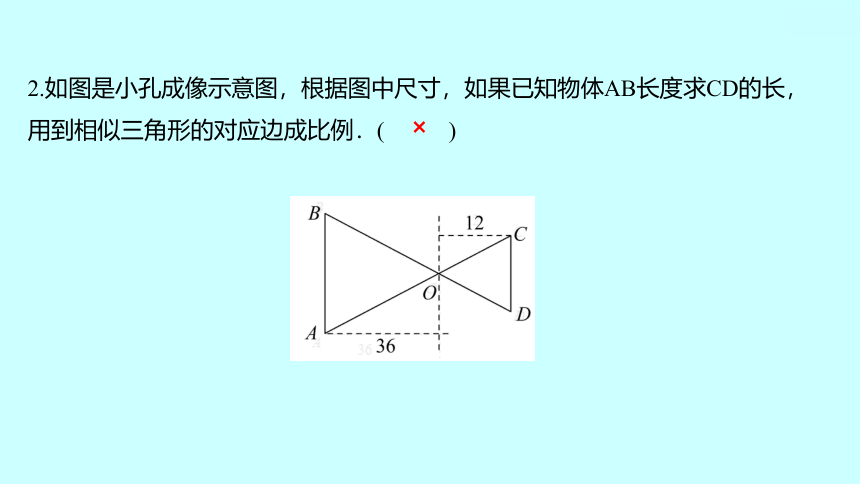
2.如图是小孔成像示意图,根据图中尺寸,如果已知物体AB长度求CD的长,
用到相似三角形的对应边成比例.( )
×
研重点·典例探析
知识点 构造相似三角形解决实际问题
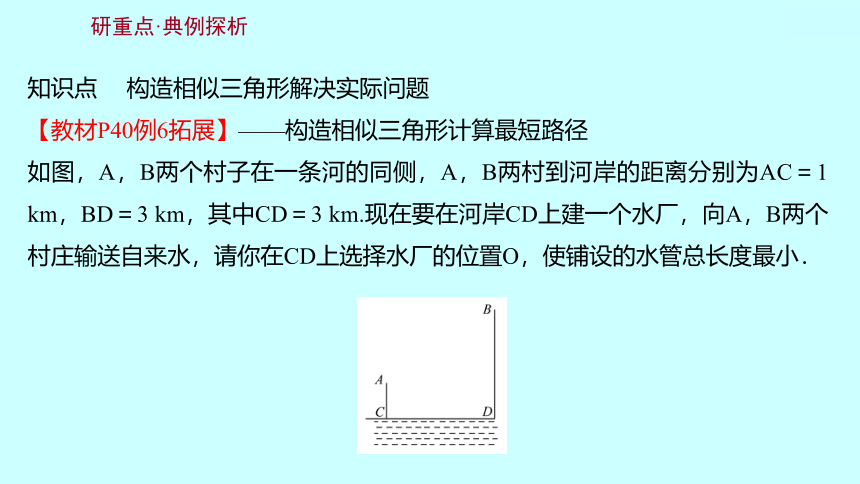
【教材P40例6拓展】——构造相似三角形计算最短路径
如图,A,B两个村子在一条河的同侧,A,B两村到河岸的距离分别为AC=1 km,BD=3 km,其中CD=3 km.现在要在河岸CD上建一个水厂,向A,B两个村庄输送自来水,请你在CD上选择水厂的位置O,使铺设的水管总长度最小.
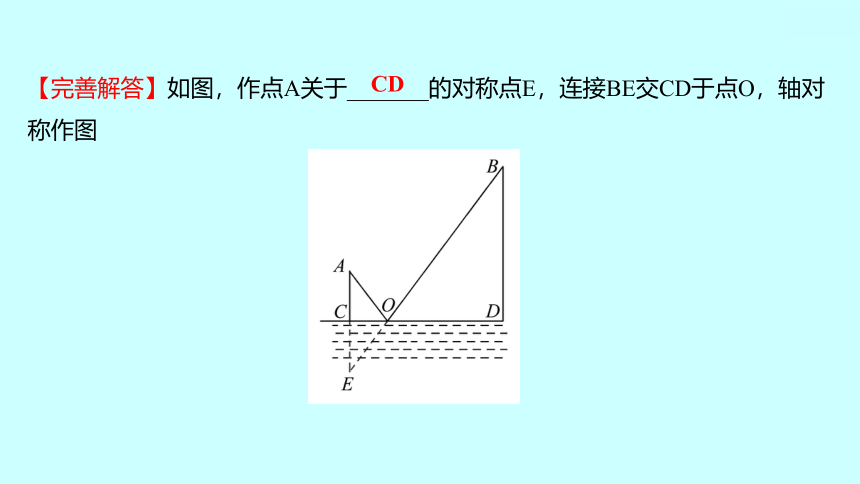
【完善解答】如图,作点A关于_______的对称点E,连接BE交CD于点O,轴对
称作图
CD
∵点A关于_______的对称点为E,
∴OA=_______,AC=_______=1 km,轴对称的性质
∴OA+_______=OE+_______=BE,等量代换
∴此时点O使OA+OB最小,
设OC=x km,则OD=__________km,
∵CE∥BD,∴△ECO∽△_________,
CD
OE
CE
OB
OB
(3-x)
BDO
0.75
0.75
【归纳提升】
变式一:巩固
(2021·南阳模拟)如图,顽皮的小聪在小芳的作业本上用笔画了个“×”(作业本中
的横格线都平行,且相邻两条横格线间的距离都相等),A,B,C,D,O都在
横格线上,且线段AD,BC交于点O.若线段AB=4 cm,则线段CD长为( )
A.4 cm B.5 cm C.6 cm D.8 cm
C
变式二:提升 如图是一个常见铁夹的剖面图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA,垂足为D,DA=15 mm,DO=24 mm,DC=10 mm,且铁夹的剖面图是轴对称图形,求A,B两点间的距离.
培素养·思维拓展
应用相似三角形进行复杂测量
1.利用平行线、标杆等构成相似三角形
2.测量与表示未知量的线段相对应的的线段的长,以及另外任意一组对应边的长度
3.画出示意图,利用相似三角形的性质,列出以上包括未知量在内的四个量的比例式,解出未知量
4.检验并得出答案
平行截线型的相似三角形
步骤
常见图形的解题方法
27.2.3相似三角形应用举例
第2课时
识新知·自主预习
【旧知再现】
1.利用_________________等工具,通过构造相似三角形,可以测量树高、
河宽等.
2.应用相似三角形进行测量时,一般要用到相似三角形对应边___________
和对应高的比等于___________.
标杆、反光镜
成比例
相似比
【新知初探】
进一步深入研讨教材P39-41,归纳有关结论
应用相似三角形进行测量的一般步骤
(1)利用平行线、标杆等构成_________三角形.
(2)测量与表示未知量的线段相对应的线段的长,以及另外任意一组对应边的
长度.
(3)画出示意图,利用相似三角形的性质,列出以上包括未知量在内的四个量
的___________,解出未知量.
(4)检验并得出答案.
相似
比例式
【妙招巧记】
相似测量分四步:
一构相似三角形,
二测有关线段长,
三是列出比例式,
四解方程写答案.
【质疑判断】
1.如图,旗杆AB的影长有一部分落在楼房的墙上,要通过测量计算旗杆的高度
AB,可以过点C作AB的垂线,也可以连接并延长AC与BD相交.( )
√
2.如图是小孔成像示意图,根据图中尺寸,如果已知物体AB长度求CD的长,
用到相似三角形的对应边成比例.( )
×
研重点·典例探析
知识点 构造相似三角形解决实际问题
【教材P40例6拓展】——构造相似三角形计算最短路径
如图,A,B两个村子在一条河的同侧,A,B两村到河岸的距离分别为AC=1 km,BD=3 km,其中CD=3 km.现在要在河岸CD上建一个水厂,向A,B两个村庄输送自来水,请你在CD上选择水厂的位置O,使铺设的水管总长度最小.
【完善解答】如图,作点A关于_______的对称点E,连接BE交CD于点O,轴对
称作图
CD
∵点A关于_______的对称点为E,
∴OA=_______,AC=_______=1 km,轴对称的性质
∴OA+_______=OE+_______=BE,等量代换
∴此时点O使OA+OB最小,
设OC=x km,则OD=__________km,
∵CE∥BD,∴△ECO∽△_________,
CD
OE
CE
OB
OB
(3-x)
BDO
0.75
0.75
【归纳提升】
变式一:巩固
(2021·南阳模拟)如图,顽皮的小聪在小芳的作业本上用笔画了个“×”(作业本中
的横格线都平行,且相邻两条横格线间的距离都相等),A,B,C,D,O都在
横格线上,且线段AD,BC交于点O.若线段AB=4 cm,则线段CD长为( )
A.4 cm B.5 cm C.6 cm D.8 cm
C
变式二:提升 如图是一个常见铁夹的剖面图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA,垂足为D,DA=15 mm,DO=24 mm,DC=10 mm,且铁夹的剖面图是轴对称图形,求A,B两点间的距离.
培素养·思维拓展
应用相似三角形进行复杂测量
1.利用平行线、标杆等构成相似三角形
2.测量与表示未知量的线段相对应的的线段的长,以及另外任意一组对应边的长度
3.画出示意图,利用相似三角形的性质,列出以上包括未知量在内的四个量的比例式,解出未知量
4.检验并得出答案
平行截线型的相似三角形
步骤
常见图形的解题方法
