2022人教版数学九年级下册 27.3.1位似课件(可编辑图片版、共26张PPT)
文档属性
| 名称 | 2022人教版数学九年级下册 27.3.1位似课件(可编辑图片版、共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 837.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 13:35:28 | ||
图片预览






文档简介
(共26张PPT)
27.3 位似
第1课时
识新知·自主预习
【旧知再现】
1._________相同的图形叫做相似图形.
2.相似多边形的对应角_________,对应边___________.
形状
相等
成比例
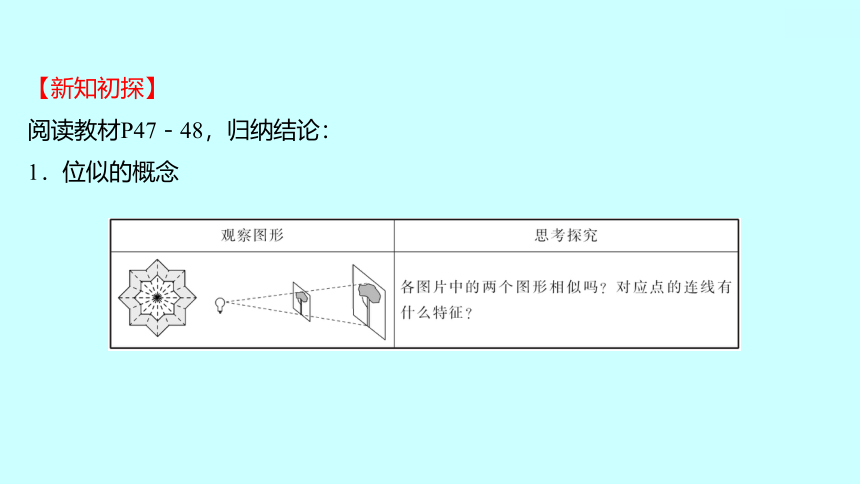
【新知初探】
阅读教材P47-48,归纳结论:
1.位似的概念
结论:
如果两个图形不仅_________,而且对应顶点的连线_______________,
这样的两个图形叫做位似图形,这个点叫做位似_________.
相似
相交于一点
中心
结论:
(1)位似图形可能在位似中心的_________,也可能在位似中心的_________.
(2)位似图形一定是_____________,每对对应点到位似中心的距离比等于
___________.
(3)位似图形中的对应线段_________(或在同一条直线上).
同侧
异侧
相似图形
相似比
平行
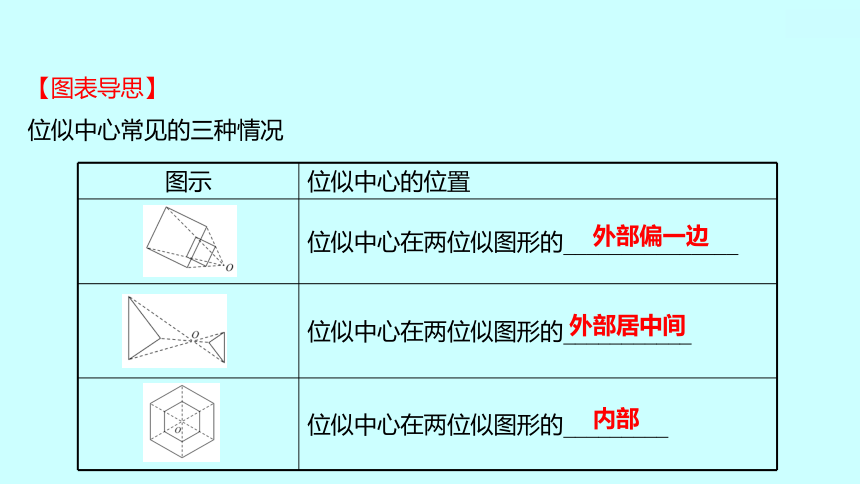
【图表导思】
位似中心常见的三种情况
图示 位似中心的位置
位似中心在两位似图形的_______________
位似中心在两位似图形的___________
位似中心在两位似图形的_________
外部偏一边
外部居中间
内部
【质疑判断】
1.相似图形一定是位似图形,位似图形一定是相似图形.( )
2.位似图形一定有位似中心.( )
3.如果两个图形是相似图形,且每组对应点连线都经过同一点,那么这两
个图形是位似图形.( )
4.位似图形上的任意两点与位似中心的距离之比都等于相似比.( )
×
√
√
×
【妙招巧记】
位似与相似,
关系是包含;
相似的性质,
位似都具备;
对应点连线,
还交同一点.
研重点·典例探析
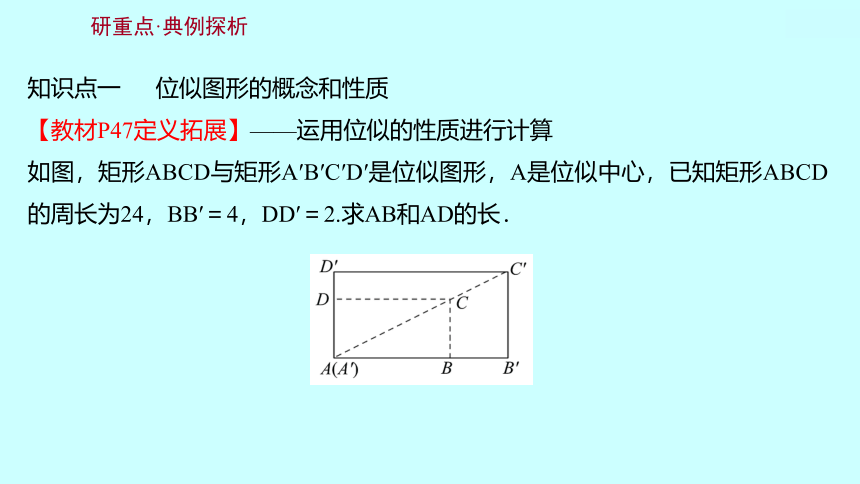
知识点一 位似图形的概念和性质
【教材P47定义拓展】——运用位似的性质进行计算
如图,矩形ABCD与矩形A′B′C′D′是位似图形,A是位似中心,已知矩形ABCD的周长为24,BB′=4,DD′=2.求AB和AD的长.
【完善解答】设AB=x,∵矩形ABCD的周长为24,
∴AD=__________,
………………矩形长宽和等于周长的一半
∵BB′=4,DD′=2,
∴AD′=AD+DD′=__________,AB′=AB+BB′=_________,……线段的和差
∵矩形ABCD与矩形A′B′C′D′是位似图形,
12-x
14-x
x+4
8
8
8
4
变式一:巩固 (2021·重庆模拟)如图,BC∥ED,下列说法不正确的是( )
A.两个三角形是位似图形
B.点A是两个三角形的位似中心
C.B与D,C与E是位似对应点
D.AE∶AD是相似比
D
变式二:提升 (2021·昆明期末)如图,△DEF是△ABC经过位似变换得到的,点O是位似中心,已知OD∶OA=1∶2,若△ABC的面积为5,
则△DEF的面积为____.
知识点二 位似变换作图
【教材P48探究拓展】——画出一个图形关于某点的位似图形
(2021·济南期末)如图,在10×10网格中,点O是格点,△ABC是格点三角形(顶点在网格线交点上),且点A1是点A以点O为位似中心的对应点.
(1)△A1B1C1与△ABC的相似比是__________;
(2)画出△ABC以点O为位似中心的位似图形△A1B1C1.
【思路点拨】(1)利用位似的性质求出OA1与OA的比得到相似比;
(2)延长OB到B1使OB1=3OB,延长OC到C1使OC1=3OC,从而得到△A1B1C1.
【自主解答】(1)△A1B1C1与△ABC的相似比为OA1∶OA=3∶1=3.
答案:3
(2)如图,△A1B1C1即为所求.
【归纳提升】
变式一:巩固 如图所示,△DEF是△ABC位似图形的几种画法,其中正确的
个数是( )
A.4 B.3 C.2 D.1
A
【解析】(1)如图,△A′B′C′为所作;
(2)如图,△A1B1C1为所作.(答案不唯一)
培素养·思维拓展
4∶9
2∶3
位似图形
概念
特点
位似作图
三确定
1.确定位似中心(两个位似图形的位似中心只有一个)
2.确定关键点
3.确定相似比
两个图形不仅相似,而且对应顶点的连线相交于一点,这样的两个图形叫做位似图形,这个点叫做位似中心
1.位似图形可能位于位似中心的同侧,也可位于位似中心的异侧
2.位似图形一定是相似图形,每对对应点到位似中心的距离比等于相似比
3.位似图形中的对应线段平行(或在同一直线上)
27.3 位似
第1课时
识新知·自主预习
【旧知再现】
1._________相同的图形叫做相似图形.
2.相似多边形的对应角_________,对应边___________.
形状
相等
成比例
【新知初探】
阅读教材P47-48,归纳结论:
1.位似的概念
结论:
如果两个图形不仅_________,而且对应顶点的连线_______________,
这样的两个图形叫做位似图形,这个点叫做位似_________.
相似
相交于一点
中心
结论:
(1)位似图形可能在位似中心的_________,也可能在位似中心的_________.
(2)位似图形一定是_____________,每对对应点到位似中心的距离比等于
___________.
(3)位似图形中的对应线段_________(或在同一条直线上).
同侧
异侧
相似图形
相似比
平行
【图表导思】
位似中心常见的三种情况
图示 位似中心的位置
位似中心在两位似图形的_______________
位似中心在两位似图形的___________
位似中心在两位似图形的_________
外部偏一边
外部居中间
内部
【质疑判断】
1.相似图形一定是位似图形,位似图形一定是相似图形.( )
2.位似图形一定有位似中心.( )
3.如果两个图形是相似图形,且每组对应点连线都经过同一点,那么这两
个图形是位似图形.( )
4.位似图形上的任意两点与位似中心的距离之比都等于相似比.( )
×
√
√
×
【妙招巧记】
位似与相似,
关系是包含;
相似的性质,
位似都具备;
对应点连线,
还交同一点.
研重点·典例探析
知识点一 位似图形的概念和性质
【教材P47定义拓展】——运用位似的性质进行计算
如图,矩形ABCD与矩形A′B′C′D′是位似图形,A是位似中心,已知矩形ABCD的周长为24,BB′=4,DD′=2.求AB和AD的长.
【完善解答】设AB=x,∵矩形ABCD的周长为24,
∴AD=__________,
………………矩形长宽和等于周长的一半
∵BB′=4,DD′=2,
∴AD′=AD+DD′=__________,AB′=AB+BB′=_________,……线段的和差
∵矩形ABCD与矩形A′B′C′D′是位似图形,
12-x
14-x
x+4
8
8
8
4
变式一:巩固 (2021·重庆模拟)如图,BC∥ED,下列说法不正确的是( )
A.两个三角形是位似图形
B.点A是两个三角形的位似中心
C.B与D,C与E是位似对应点
D.AE∶AD是相似比
D
变式二:提升 (2021·昆明期末)如图,△DEF是△ABC经过位似变换得到的,点O是位似中心,已知OD∶OA=1∶2,若△ABC的面积为5,
则△DEF的面积为____.
知识点二 位似变换作图
【教材P48探究拓展】——画出一个图形关于某点的位似图形
(2021·济南期末)如图,在10×10网格中,点O是格点,△ABC是格点三角形(顶点在网格线交点上),且点A1是点A以点O为位似中心的对应点.
(1)△A1B1C1与△ABC的相似比是__________;
(2)画出△ABC以点O为位似中心的位似图形△A1B1C1.
【思路点拨】(1)利用位似的性质求出OA1与OA的比得到相似比;
(2)延长OB到B1使OB1=3OB,延长OC到C1使OC1=3OC,从而得到△A1B1C1.
【自主解答】(1)△A1B1C1与△ABC的相似比为OA1∶OA=3∶1=3.
答案:3
(2)如图,△A1B1C1即为所求.
【归纳提升】
变式一:巩固 如图所示,△DEF是△ABC位似图形的几种画法,其中正确的
个数是( )
A.4 B.3 C.2 D.1
A
【解析】(1)如图,△A′B′C′为所作;
(2)如图,△A1B1C1为所作.(答案不唯一)
培素养·思维拓展
4∶9
2∶3
位似图形
概念
特点
位似作图
三确定
1.确定位似中心(两个位似图形的位似中心只有一个)
2.确定关键点
3.确定相似比
两个图形不仅相似,而且对应顶点的连线相交于一点,这样的两个图形叫做位似图形,这个点叫做位似中心
1.位似图形可能位于位似中心的同侧,也可位于位似中心的异侧
2.位似图形一定是相似图形,每对对应点到位似中心的距离比等于相似比
3.位似图形中的对应线段平行(或在同一直线上)
