2022人教版数学九年级下册 27.2.1.3相似三角形的判定课件(可编辑图片版、共32张PPT)
文档属性
| 名称 | 2022人教版数学九年级下册 27.2.1.3相似三角形的判定课件(可编辑图片版、共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 13:48:21 | ||
图片预览





文档简介
(共32张PPT)
27.2 相似三角形
27.2.1 相似三角形的判定
第3课时
识新知·自主预习
【旧知再现】
1.三边___________的两个三角形相似.
2.两边___________且夹角_________的两个三角形相似.
成比例
成比例
相等
【新知初探】
阅读教材P35-36,完成探究过程,归纳有关结论:
1.利用两组角判定三角形相似的定理
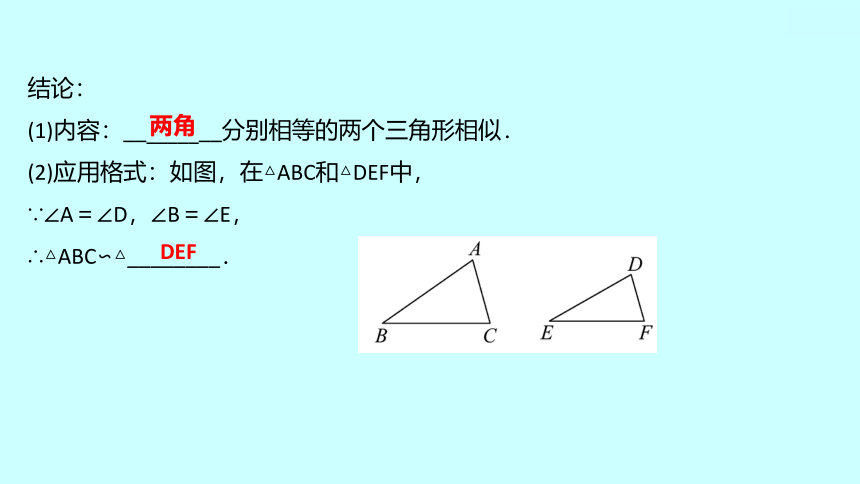
结论:
(1)内容:_________分别相等的两个三角形相似.
(2)应用格式:如图,在△ABC和△DEF中,
∵∠A=∠D,∠B=∠E,
∴△ABC∽△________.
两角
DEF
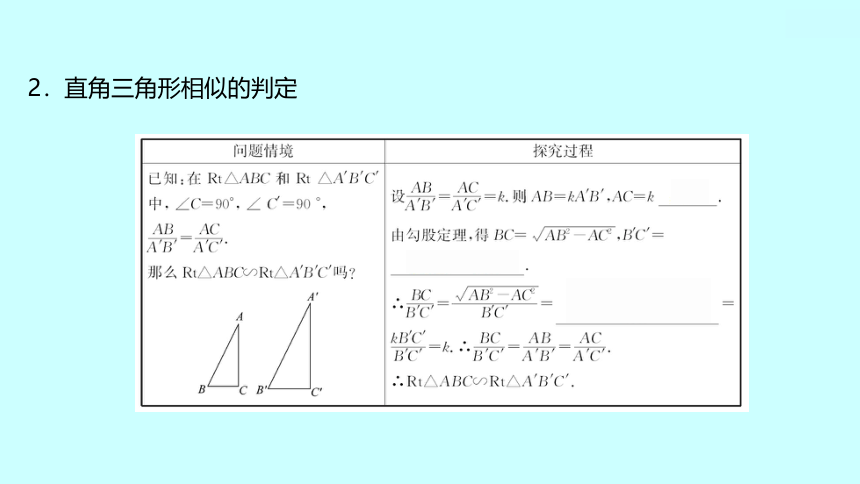
2.直角三角形相似的判定
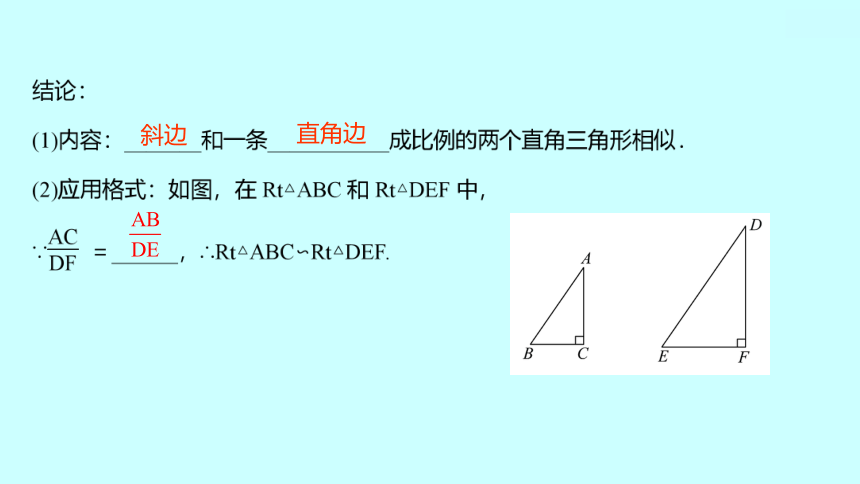
斜边
直角边
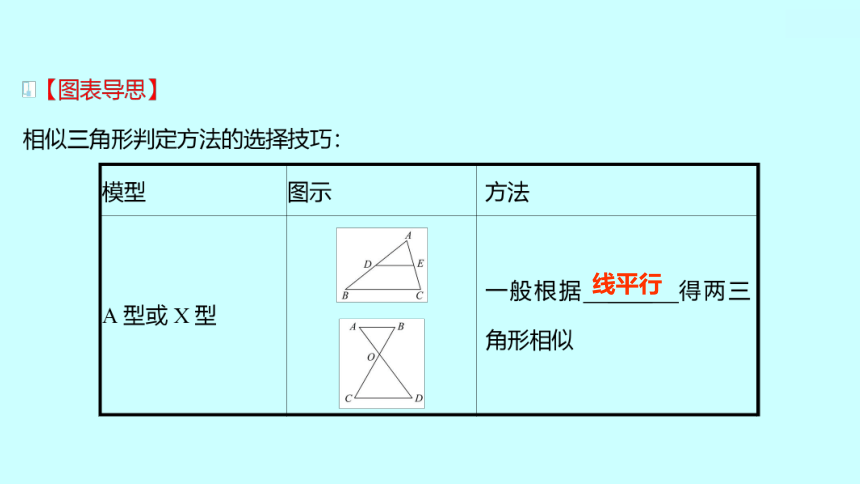
线平行
相等
两边
夹角
两角相等
两角相等
两边
夹角
【质疑判断】
1.一个锐角对应相等的两个直角三角形相似.( )
2.一条直角边和斜边对应成比例的两个直角三角形相似.( )
3.两条直角边对应成比例的两个直角三角形不一定相似.( )
√
√
×
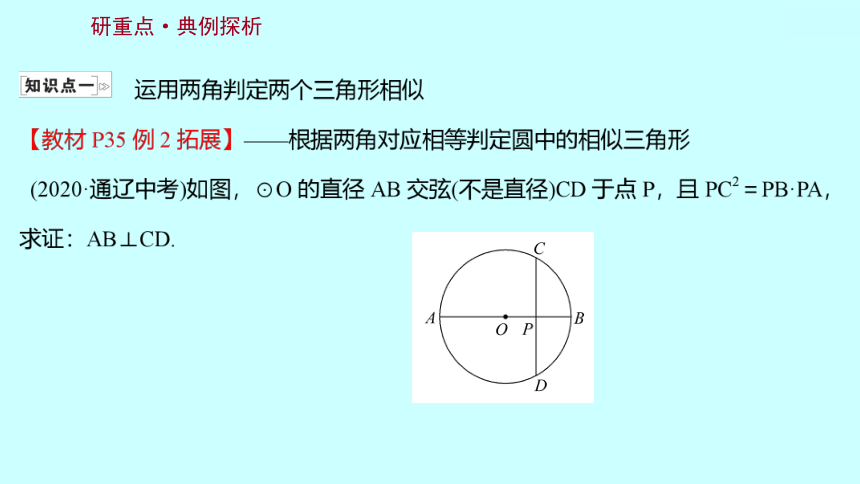
研重点·典例探析
规范书写 证明:连接AC,BD,如图,
∵∠A=∠D,∠C=∠B,①
∴△APC∽△DPB,
∴PC∶PB=PA∶PD,
∴PC·PD=PB·PA,②
∵PC2=PB·PA,∴PC2=PC·PD,
∴PC=PD,
∵AB为直径,
∴AB⊥CD.③
【完善解答】∵CD,C′D′分别为Rt△ABC和Rt△A′B′C′的高,∴∠ADC=___________
=90°. ……………………三角形高线的特征
又∵=,∴Rt△ADC∽_____________,………………………………
斜边和一条直角边成比例的两个直角三角形相似
∴∠A=________.………………相似三角形的对应角相等
又∵∠ACB=___________=90°,∴△ABC∽___________.……两角对应相等的两个
三角形相似
∠A′D′C′
Rt△A′D′C′
∠A′
∠A′C′B′
△A′B′C′
【归纳提升】
培素养·思维拓展
△ACP
△CBP
2
相似三角形的判定
判定4
直角三角形相似判定
一个锐角相等或者两组直角边成比例的两个直角三角形相似,斜边和一条直角边成比例的两个直角三角形相似
两角分别相等的两个三角形相似
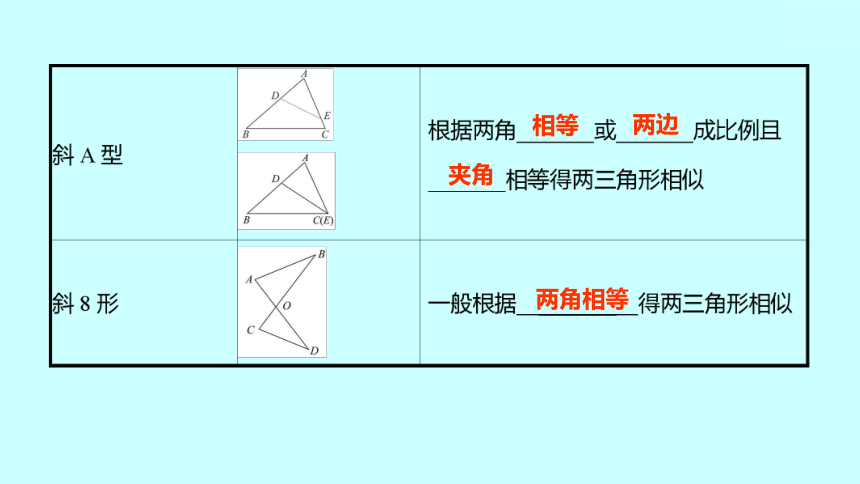
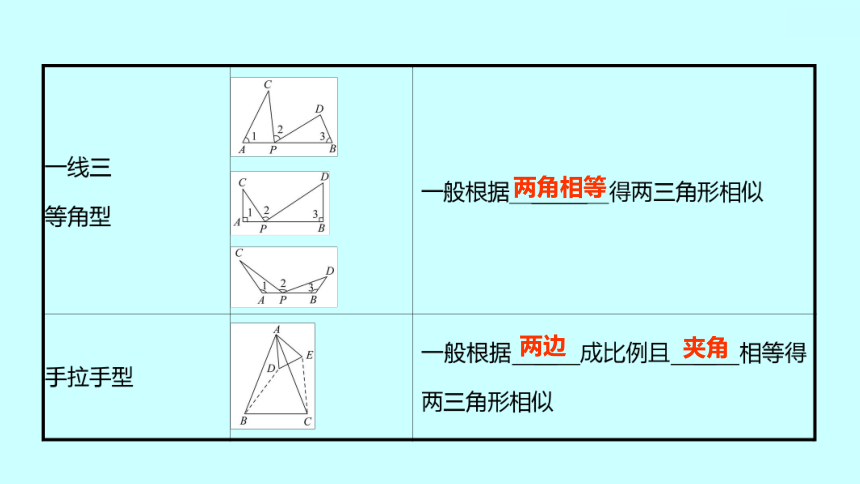
两三角形相似的几种类型:
1.平行线型
2.相交线型(四种图形)
3.旋转型
27.2 相似三角形
27.2.1 相似三角形的判定
第3课时
识新知·自主预习
【旧知再现】
1.三边___________的两个三角形相似.
2.两边___________且夹角_________的两个三角形相似.
成比例
成比例
相等
【新知初探】
阅读教材P35-36,完成探究过程,归纳有关结论:
1.利用两组角判定三角形相似的定理
结论:
(1)内容:_________分别相等的两个三角形相似.
(2)应用格式:如图,在△ABC和△DEF中,
∵∠A=∠D,∠B=∠E,
∴△ABC∽△________.
两角
DEF
2.直角三角形相似的判定
斜边
直角边
线平行
相等
两边
夹角
两角相等
两角相等
两边
夹角
【质疑判断】
1.一个锐角对应相等的两个直角三角形相似.( )
2.一条直角边和斜边对应成比例的两个直角三角形相似.( )
3.两条直角边对应成比例的两个直角三角形不一定相似.( )
√
√
×
研重点·典例探析
规范书写 证明:连接AC,BD,如图,
∵∠A=∠D,∠C=∠B,①
∴△APC∽△DPB,
∴PC∶PB=PA∶PD,
∴PC·PD=PB·PA,②
∵PC2=PB·PA,∴PC2=PC·PD,
∴PC=PD,
∵AB为直径,
∴AB⊥CD.③
【完善解答】∵CD,C′D′分别为Rt△ABC和Rt△A′B′C′的高,∴∠ADC=___________
=90°. ……………………三角形高线的特征
又∵=,∴Rt△ADC∽_____________,………………………………
斜边和一条直角边成比例的两个直角三角形相似
∴∠A=________.………………相似三角形的对应角相等
又∵∠ACB=___________=90°,∴△ABC∽___________.……两角对应相等的两个
三角形相似
∠A′D′C′
Rt△A′D′C′
∠A′
∠A′C′B′
△A′B′C′
【归纳提升】
培素养·思维拓展
△ACP
△CBP
2
相似三角形的判定
判定4
直角三角形相似判定
一个锐角相等或者两组直角边成比例的两个直角三角形相似,斜边和一条直角边成比例的两个直角三角形相似
两角分别相等的两个三角形相似
两三角形相似的几种类型:
1.平行线型
2.相交线型(四种图形)
3.旋转型
