福州文博中学2012级第一章《集合》单元测试卷(含答案)
文档属性
| 名称 | 福州文博中学2012级第一章《集合》单元测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 160.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-13 00:00:00 | ||
图片预览


文档简介
福州文博中学2012级第一章《集合》单元测试卷
第一部分 基础演练(150分)
一、选择题.(每小题有且只有一个正确答案,5分×12=60分)
1、已知全集U = {1 ,2 ,3 ,4 ,5 ,6 ,7 }, A= {3 ,4 ,5 },
B= {1 ,3 ,6 },那么集合 { 2 ,7 }是 ( )
A. B. C. D.
2 . 如果集合A={x|ax2+2x+1=0}中只有一个元素,则a的值是 ( )
A.0 B.0 或1 C.1 D.不能确定
3. 设集合A={x|1<x<2},B={x|x<a}满足A B,则实数a的取值范围是( )
A.{a|a ≥2} B.{a|a≤1} C.{a|a≥1}. D.{a|a≤2}.
4. 满足{1,2,3} M {1,2,3,4,5,6}的集合M的个数是 ( )
A.8 B.7 C.6 D.5
5.下列四种说法中,不正确的是 ( )
A.若函数的定义域只含有一个元素,则值域也只含有一个元素.
B.若函数的定义域含有无数多个元素,则值域也含有无数多个元素.
C.定义域和对应法则确定后,函数的值域也就确定了.
D.定义域和值域相同的两个函数,有可能不是同一个函数.
6.下列各图中,可表示函数y=f(x)的图象只可能是 ( )
A B C D
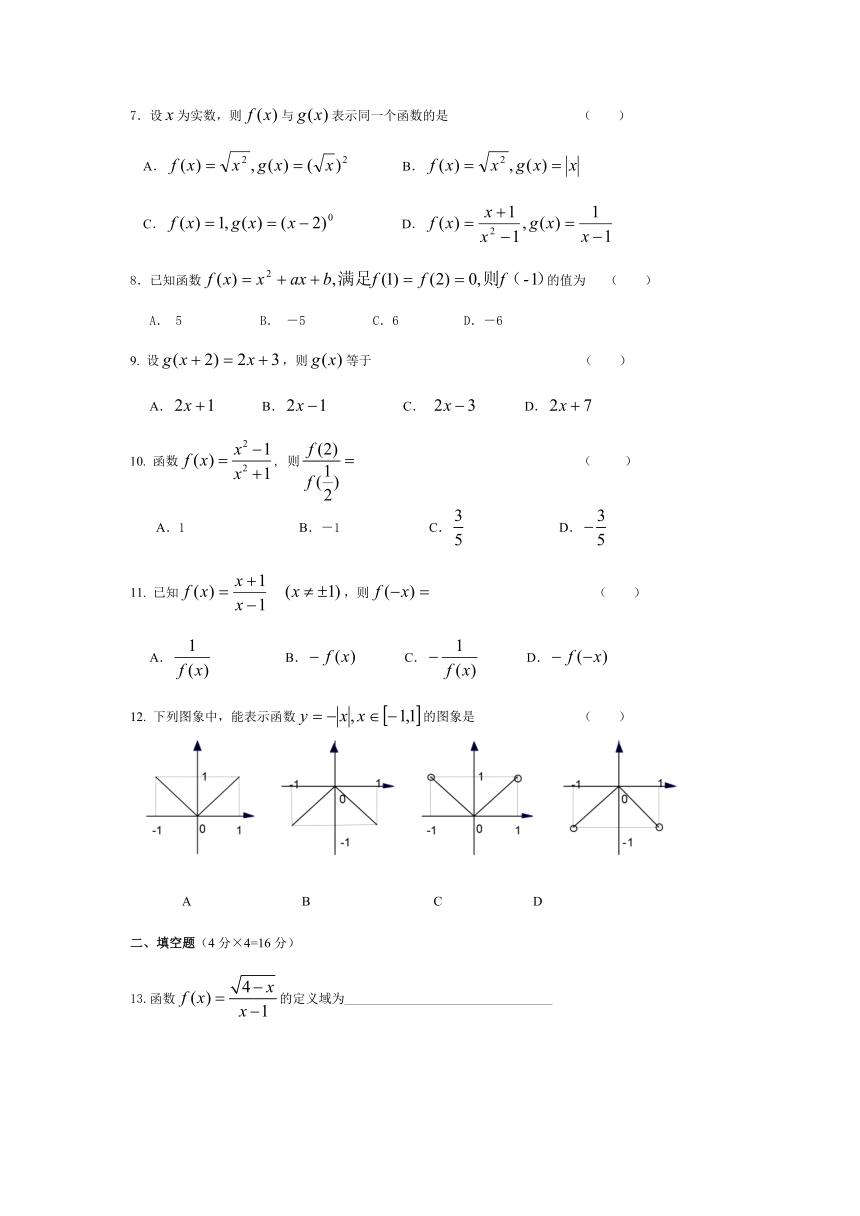
7.设为实数,则与表示同一个函数的是 ( )
A. B.
C. D.
8.已知函数的值为 ( )
A. 5 B. -5 C.6 D.-6
9. 设,则等于 ( )
A. B. C. D.
10. 函数, 则 ( )
A.1 B.-1 C. D.
11. 已知 ,则 ( )
A. B. C. D.
12. 下列图象中,能表示函数的图象是 ( )
A B C D
二、填空题(4分×4=16分)
13.函数的定义域为________________________________
14.函数则
15. 某城市出租车按如下方法收费,起步价6元,可行3km,3km到10km每走1km加价1元,10km后每走1km加价0.8元,某人坐出租车走了12km,他应交费_______________元
16. 集合M={a| ∈N,且a∈Z},用列举法表示集合M=
三、解答题.(74分)
17.(12分) 设U={x∈Z|0求CUA)(CUB),。
18.(12分)设集合A={a2,a+1,-1},B={2a-1,| a-2 |, 3a2+4},A∩B={-1},求实数a的值.
19.(14分)求下列函数的值域
(1) (2)
20.(12分)已知求函数的定义域.
21. (12分)已知,,为的一次函数,求
22. (12分)已知,求,
第二部分 能力提高 (20分)
1.设U={1,2,3,4,5},若A∩B={2},(CUA)∩B={4},(CUA)∩(CUB)={1,5},则下列结论正确的是( )
A.3A且3B B.3B且3∈A C.3A且3∈B D.3∈A且3∈B
2.两个不同函数为常数)的定义域都是R,如果它们的值域也相同,则a=______________
3.已知函数的定义域为R,求实数的取值范围
福州文博中学2012级第一章《集合》单元测试卷答案
一、选择题.(,5分×12=60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
A
C
B
C
B
C
B
B
A
B
二、填空题(4分×4=16分)
13.{x| x4 且x1} 14. 15.14.6 16.{-1, 2, 3, 4}
三、解答题.(74分)
17.(12分) 解:={1,2,4,5,6,7,8,9,10}, CUA={3,6,7,8,10} CUB={1,2,3,5,9}
(CUA)(CUB)={1,2,3,5,6,7,8,9,10}, ={4} =
18.(12分)解: A∩B={-1} -1B.而| a-2 |>0,3a2+4>0 2a-1=-1 a=0
此时 A={0, 1,-1} B={-1,2,4}符合题意
19.(14分)解:(1)=,由0得0 -1x5
-3x-23 0(x-2)29 03
即函数的值域为[0,3]
(2)设=t( t0),则x=.
即函数的值域为[2,+)
20.(12分)解: 中的满足
即
函数的定义域为[-2,2]
21. (12分)解:为的一次函数,可设,则 又
比较系数有 解得
22. (12分)解:在中令得=0,设 则, ,
第二部分 能力提高 (20分)
1.B, 2. a=-5
3.解:函数的定义域为R, 对恒成立
或
即或 的取值范围是[0,1]
第一部分 基础演练(150分)
一、选择题.(每小题有且只有一个正确答案,5分×12=60分)
1、已知全集U = {1 ,2 ,3 ,4 ,5 ,6 ,7 }, A= {3 ,4 ,5 },
B= {1 ,3 ,6 },那么集合 { 2 ,7 }是 ( )
A. B. C. D.
2 . 如果集合A={x|ax2+2x+1=0}中只有一个元素,则a的值是 ( )
A.0 B.0 或1 C.1 D.不能确定
3. 设集合A={x|1<x<2},B={x|x<a}满足A B,则实数a的取值范围是( )
A.{a|a ≥2} B.{a|a≤1} C.{a|a≥1}. D.{a|a≤2}.
4. 满足{1,2,3} M {1,2,3,4,5,6}的集合M的个数是 ( )
A.8 B.7 C.6 D.5
5.下列四种说法中,不正确的是 ( )
A.若函数的定义域只含有一个元素,则值域也只含有一个元素.
B.若函数的定义域含有无数多个元素,则值域也含有无数多个元素.
C.定义域和对应法则确定后,函数的值域也就确定了.
D.定义域和值域相同的两个函数,有可能不是同一个函数.
6.下列各图中,可表示函数y=f(x)的图象只可能是 ( )
A B C D
7.设为实数,则与表示同一个函数的是 ( )
A. B.
C. D.
8.已知函数的值为 ( )
A. 5 B. -5 C.6 D.-6
9. 设,则等于 ( )
A. B. C. D.
10. 函数, 则 ( )
A.1 B.-1 C. D.
11. 已知 ,则 ( )
A. B. C. D.
12. 下列图象中,能表示函数的图象是 ( )
A B C D
二、填空题(4分×4=16分)
13.函数的定义域为________________________________
14.函数则
15. 某城市出租车按如下方法收费,起步价6元,可行3km,3km到10km每走1km加价1元,10km后每走1km加价0.8元,某人坐出租车走了12km,他应交费_______________元
16. 集合M={a| ∈N,且a∈Z},用列举法表示集合M=
三、解答题.(74分)
17.(12分) 设U={x∈Z|0
18.(12分)设集合A={a2,a+1,-1},B={2a-1,| a-2 |, 3a2+4},A∩B={-1},求实数a的值.
19.(14分)求下列函数的值域
(1) (2)
20.(12分)已知求函数的定义域.
21. (12分)已知,,为的一次函数,求
22. (12分)已知,求,
第二部分 能力提高 (20分)
1.设U={1,2,3,4,5},若A∩B={2},(CUA)∩B={4},(CUA)∩(CUB)={1,5},则下列结论正确的是( )
A.3A且3B B.3B且3∈A C.3A且3∈B D.3∈A且3∈B
2.两个不同函数为常数)的定义域都是R,如果它们的值域也相同,则a=______________
3.已知函数的定义域为R,求实数的取值范围
福州文博中学2012级第一章《集合》单元测试卷答案
一、选择题.(,5分×12=60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
A
C
B
C
B
C
B
B
A
B
二、填空题(4分×4=16分)
13.{x| x4 且x1} 14. 15.14.6 16.{-1, 2, 3, 4}
三、解答题.(74分)
17.(12分) 解:={1,2,4,5,6,7,8,9,10}, CUA={3,6,7,8,10} CUB={1,2,3,5,9}
(CUA)(CUB)={1,2,3,5,6,7,8,9,10}, ={4} =
18.(12分)解: A∩B={-1} -1B.而| a-2 |>0,3a2+4>0 2a-1=-1 a=0
此时 A={0, 1,-1} B={-1,2,4}符合题意
19.(14分)解:(1)=,由0得0 -1x5
-3x-23 0(x-2)29 03
即函数的值域为[0,3]
(2)设=t( t0),则x=.
即函数的值域为[2,+)
20.(12分)解: 中的满足
即
函数的定义域为[-2,2]
21. (12分)解:为的一次函数,可设,则 又
比较系数有 解得
22. (12分)解:在中令得=0,设 则, ,
第二部分 能力提高 (20分)
1.B, 2. a=-5
3.解:函数的定义域为R, 对恒成立
或
即或 的取值范围是[0,1]
