第三章不等式 章末测评-2021-2022学年高一下学期数学北师大版必修5(Word含答案解析)
文档属性
| 名称 | 第三章不等式 章末测评-2021-2022学年高一下学期数学北师大版必修5(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 390.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 09:58:05 | ||
图片预览




文档简介
第三章 章末测评
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.不等式组的解集为( )
A.{x|-2<x<-1}
B.{x|-1<x<0}
C.{x|0<x<1}
D.{x|x>1}
2.若集合A=,B={x|y=log2[(2-x)(1+x)]},则A∩B=( )
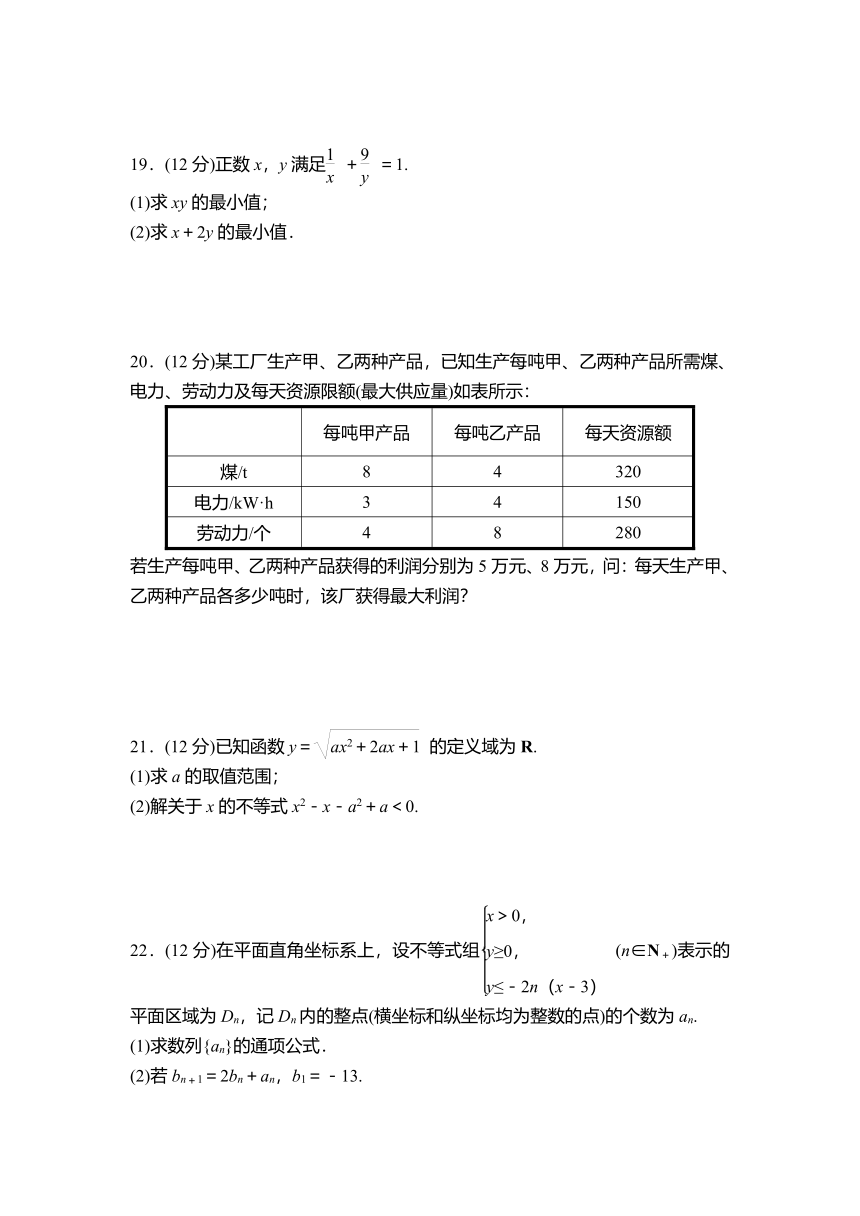
A.[-2,2) B.(-1,1)
C.(-1,1] D.(-1,2)
3.已知M=2a(a-2),N=(a+1)(a-3),则M,N的大小关系是( )
A.M>N B.M≥N
C.M4.不等式(x-2y+1)(x+y-3)≤0在平面直角坐标系内表示的区域(用阴影部分表示),应是下列图形中的( )
5.不等式≥1的解集为( )
A.(-∞,-1]∪[2,+∞)
B.(-∞,-1]∪
C.(-∞,-1]∪
D.∪[2,+∞)
6.不等式ax2+bx+2>0的解集是(-,),则a+b的值是( )
A.10 B.-10 C.-14 D.14
7.已知x,y满足约束条件当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2时,a2+b2的最小值为( )
A.5 B.4 C. D.2
8.若一元二次方程x2+(a-1)x+1-a2=0有两个正实数根,则a的取值范围是( )
A.(-1,1)
B.∪[1,+∞)
C.
D.
9.已知x>0,y>0,lg 2x+lg 8y=lg 2,则+的最小值是( )
A.2 B.2 C.4 D.2
10.已知z=2x+y,x,y满足且z的最大值是最小值的4倍,则实数a的值是( )
A. B. C. D.
11.某公司租地建仓库,每月土地费用与仓库到车站距离成反比,而每月货物的运输费用与仓库到车站距离成正比.如果在距离车站10 km处建仓库,则土地费用和运输费用分别为2万元和8万元,那么要使两项费用之和最小,仓库应建在离车站( )
A.5 km处 B.4 km处
C.3 km处 D.2 km处
12.已知-1≤x+y≤4,且2≤x-y≤3,则z=2x-3y的取值范围是( )
A.[3,8] B.[3,6]
C.[6,7] D.[4,5]
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)
13.某小型服装厂生产一种风衣,日销货量x件与货价p元/件之间的关系为p=160-2x,生产x件所需成本为C=500+30x元,则该厂日产量为______时,日获利不少于1 300元.
14.已知a,b,x,y∈(0,+∞),且+=1,x2+y2=8,则ab与xy的大小关系为____.
15.已知实数a,b,c满足a+b+c=0,a2+b2+c2=1,则a的最大值是________.
16.(2020·全国Ⅱ卷)若x,y满足约束条件则z=x+2y的最大值是________.
三、解答题(共70分)
17.(10分)已知实数x,y满足
(1)z=的取值范围;
(2)z=x2+y2-10y+25的最小值.
18.(12分)某厂家拟在2020年举行促销活动,经调查测算,某产品的年销售量(即该厂的年产量)m万件与年促销费用x万元,满足m=3-(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2020年该产品的利润y(万元)表示为年促销费用x(万元)的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
19.(12分)正数x,y满足+=1.
(1)求xy的最小值;
(2)求x+2y的最小值.
20.(12分)某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力及每天资源限额(最大供应量)如表所示:
每吨甲产品 每吨乙产品 每天资源额
煤/t 8 4 320
电力/kW·h 3 4 150
劳动力/个 4 8 280
若生产每吨甲、乙两种产品获得的利润分别为5万元、8万元,问:每天生产甲、乙两种产品各多少吨时,该厂获得最大利润?
21.(12分)已知函数y=的定义域为R.
(1)求a的取值范围;
(2)解关于x的不等式x2-x-a2+a<0.
22.(12分)在平面直角坐标系上,设不等式组(n∈N+)表示的平面区域为Dn,记Dn内的整点(横坐标和纵坐标均为整数的点)的个数为an.
(1)求数列{an}的通项公式.
(2)若bn+1=2bn+an,b1=-13.
求证:数列{bn+6n+9}是等比数列,并求出数列{bn}的通项公式.
答案解析
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.不等式组的解集为( )
A.{x|-2<x<-1}
B.{x|-1<x<0}
C.{x|0<x<1}
D.{x|x>1}
【解析】选C.原不等式组可化为
,解得0<x<1.
2.若集合A=,B={x|y=log2[(2-x)(1+x)]},则A∩B=( )
A.[-2,2) B.(-1,1)
C.(-1,1] D.(-1,2)
【解析】选B.不等式≤0,等价于(x+2)(x-1)≤0且x-1≠0,解得-2≤x<1,即A=.
函数y=log2的定义域为(2-x)(1+x)>0,解得-13.已知M=2a(a-2),N=(a+1)(a-3),则M,N的大小关系是( )
A.M>N B.M≥N
C.M【解析】选A.因为M-N=2a(a-2)-(a+1)(a-3)=a2-2a+3=(a-1)2+2>0,所以M>N.
4.不等式(x-2y+1)(x+y-3)≤0在平面直角坐标系内表示的区域(用阴影部分表示),应是下列图形中的( )
【解析】选C.(x-2y+1)(x+y-3)≤0等价于或
即不等式表示的区域是同时在两直线的上方或同时在两直线的下方,只有C项符合.
5.不等式≥1的解集为( )
A.(-∞,-1]∪[2,+∞)
B.(-∞,-1]∪
C.(-∞,-1]∪
D.∪[2,+∞)
【解析】选D.由题得-1≥0,
所以≥0,所以≥0,
所以
所以-1≤x<或x≥2.即该不等式的解集为∪[2,+∞).
6.不等式ax2+bx+2>0的解集是(-,),则a+b的值是( )
A.10 B.-10 C.-14 D.14
【解析】选C.因为不等式ax2+bx+2>0的解集是,所以方程ax2+bx+2=0的两根为-和.所以所以a+b=-14.
7.已知x,y满足约束条件当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2时,a2+b2的最小值为( )
A.5 B.4 C. D.2
【解析】选B.约束条件满足的可行域如图中的阴影部分所示.由图可知,目标函数z=ax+by(a>0,b>0)取最小值时,最优解为(2,1).
所以2a+b=2,则b=2-2a,
所以a2+b2=a2+(2-2a)2=5a2-8a+20=52+4,即当a=,b=时,a2+b2有最小值4.
8.若一元二次方程x2+(a-1)x+1-a2=0有两个正实数根,则a的取值范围是( )
A.(-1,1)
B.∪[1,+∞)
C.
D.
【解析】选C.因为方程有两个正实数根,不妨设为x1,x2,
所以有
即所以-1<a≤-.
9.已知x>0,y>0,lg 2x+lg 8y=lg 2,则+的最小值是( )
A.2 B.2 C.4 D.2
【解析】选C.由lg 2x+lg 8y=lg 2,得lg 2x+3y=lg 2,所以x+3y=1,+=(+)(x+3y)=2++≥4.
当且仅当即时,等号成立.
故+的最小值是4.
10.已知z=2x+y,x,y满足且z的最大值是最小值的4倍,则实数a的值是( )
A. B. C. D.
【解析】选B.在坐标平面内画出题中的不等式组表示的平面区域(图略)及直线2x+y=0,平移该直线,当相应直线分别经过该平面区域内的点(a,a)与(1,1)时,相应直线在y轴上的截距达到最小与最大,此时z=2x+y取得最小值与最大值,于是有2×1+1=4(2a+a),a=.
11.某公司租地建仓库,每月土地费用与仓库到车站距离成反比,而每月货物的运输费用与仓库到车站距离成正比.如果在距离车站10 km处建仓库,则土地费用和运输费用分别为2万元和8万元,那么要使两项费用之和最小,仓库应建在离车站( )
A.5 km处 B.4 km处
C.3 km处 D.2 km处
【解析】选A.设车站到仓库距离为x km(x>0),土地费用为y1万元,运输费用为y2万元,由题意得y1=,y2=k2x,
因为x=10时,y1=2,y2=8,
所以k1=20,k2=,所以费用之和为y=y1+y2=+x≥2=8,当且仅当=,即x=5时取等号.
12.已知-1≤x+y≤4,且2≤x-y≤3,则z=2x-3y的取值范围是( )
A.[3,8] B.[3,6]
C.[6,7] D.[4,5]
【解析】(方法一)
选A.作出不等式组表示的可行域,如图中阴影部分(含边界)所示.
在可行域内平移直线2x-3y=0,当直线经过x-y=2与x+y=4的交点A(3,1)时,目标函数有最小值,zmin=2×3-3×1=3;当直线经过x+y=-1与x-y=3的交点B(1,-2)时,目标函数有最大值,zmax=2×1+3×2=8.所以z∈[3,8].
(方法二)选A.设2x-3y=λ(x+y)+μ(x-y),则(λ+μ)x+(λ-μ)y=2x-3y,
所以解得
所以z=-(x+y)+(x-y).
因为-1≤x+y≤4,所以-2≤-(x+y)≤.①
因为2≤x-y≤3,所以5≤(x-y)≤.②
①+②得,3≤-(x+y)+(x-y)≤8,
所以z的取值范围是[3,8].
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)
13.某小型服装厂生产一种风衣,日销货量x件与货价p元/件之间的关系为p=160-2x,生产x件所需成本为C=500+30x元,则该厂日产量为______时,日获利不少于1 300元.
【解析】由题意,得(160-2x)x-(500+30x)≥1 300,化简得x2-65x+900≤0,解得20≤x≤45.因此,该厂日产量为20件至45件时,日获利不少于1 300元.
答案:20件至45件
14.已知a,b,x,y∈(0,+∞),且+=1,x2+y2=8,则ab与xy的大小关系为____.
【解析】因为1=+≥2=,所以ab≥4.因为8=x2+y2≥2xy,所以xy≤4.所以ab≥4≥xy.
答案:ab≥xy
15.已知实数a,b,c满足a+b+c=0,a2+b2+c2=1,则a的最大值是________.
【解析】因为a+b+c=0,所以b+c=-a.
因为a2+b2+c2=1,所以-a2+1=b2+c2=(b+c)2-2bc=a2-2bc,所以2a2-1=2bc≤b2+c2=1-a2,所以3a2≤2,所以a2≤,所以-≤a≤.所以amax=.
答案:
16.(2020·全国Ⅱ卷)若x,y满足约束条件则z=x+2y的最大值是________.
【解析】不等式组表示的平面区域如图阴影部分(含边界)所示:
平移直线y=-x,当直线经过点A时,直线y=-x+z在纵轴上的截距最大,此时点A的坐标是方程组的解,
解得:
因此z=x+2y的最大值为2+2×3=8.
答案:8
三、解答题(共70分)
17.(10分)已知实数x,y满足
(1)z=的取值范围;
(2)z=x2+y2-10y+25的最小值.
【解析】作出可行域如图所示,并求出各点的坐标为A(1,3),B(3,1),C(7,9),Q(-1,-).
(1)将z=变形为z=2×,由斜率公式可知表示可行域内任一点(x,y)与定点Q连线的斜率的两倍,
因此kQ A==,kQB==,故z的范围为.
(2)z=x2+y2-10y+25=x2+(y-5)2表示可行域内任一点(x,y)到定点M(0,5)的距离的平方,
过M作直线AC的垂线,易知垂足N在线段AC上,M(0,5),直线AC:x-y+2=0,
故由点到直线距离公式可得|MN|==,
所以z的最小值是|MN|2=.
18.(12分)某厂家拟在2020年举行促销活动,经调查测算,某产品的年销售量(即该厂的年产量)m万件与年促销费用x万元,满足m=3-(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2020年该产品的利润y(万元)表示为年促销费用x(万元)的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
【解析】(1)由题意知,当x=0时,m=1,
所以1=3-k,k=2,m=3-,
每件产品的销售价格为1.5×元.
所以2020年的利润y=1.5×·m-8-16m-x=--x+28(x≥0).
(2)由(1)知,y=--x+28=--(x+1)+29 =-+29≤
-2+29=21,
当且仅当=(x+1),即x=3时取等号,该厂家2020年的促销费用投入3万元时,厂家的利润最大,为21万元.
19.(12分)正数x,y满足+=1.
(1)求xy的最小值;
(2)求x+2y的最小值.
【解析】(1)由1=+≥2得xy≥36,当且仅当=,即y=9x=18时取等号,故xy的最小值为36.
(2)由题意可得x+2y=(x+2y)(+)=19++≥19+2=19+6,当且仅当=,即9x2=2y2时取等号,故x+2y的最小值为19+6.
20.(12分)某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力及每天资源限额(最大供应量)如表所示:
每吨甲产品 每吨乙产品 每天资源额
煤/t 8 4 320
电力/kW·h 3 4 150
劳动力/个 4 8 280
若生产每吨甲、乙两种产品获得的利润分别为5万元、8万元,问:每天生产甲、乙两种产品各多少吨时,该厂获得最大利润?
【解析】设此工厂每天分别生产甲、乙两种产品x吨,y吨,获得利润z万元,
依题意可得约束条件
作出可行域,如图阴影部分所示.
利润目标函数z=5x+8y.
由几何意义知,当直线y=-x+z经过可行域上的点M时,z=5x+8y取最大值.
解方程组得
即M(10,30).所以每天生产甲种产品10吨,乙种产品30吨时,该厂获得最大利润.
21.(12分)已知函数y=的定义域为R.
(1)求a的取值范围;
(2)解关于x的不等式x2-x-a2+a<0.
【解析】(1)因为函数y=的定义域为R,
所以ax2+2ax+1≥0,恒成立.
①当a=0时,1≥0恒成立;
②当a≠0时,则
解得0<a≤1.
综上,a的取值范围为[0,1].
(2)由x2-x-a2+a<0得,(x-a)[x-(1-a)]<0.
因为0≤a≤1,所以①当1-a>a,
即0≤a<时,a<x<1-a;
②当1-a=a,即a=时,<0,不等式无解;
③当1-a<a,即<a≤1时1-a<x<a.
综上所述,当0≤a<时,解集为(a,1-a);
当a=时,解集为;当<a≤1时,解集为(1-a,a).
22.(12分)在平面直角坐标系上,设不等式组(n∈N+)表示的平面区域为Dn,记Dn内的整点(横坐标和纵坐标均为整数的点)的个数为an.
(1)求数列{an}的通项公式.
(2)若bn+1=2bn+an,b1=-13.
求证:数列{bn+6n+9}是等比数列,并求出数列{bn}的通项公式.
【解析】(1)根据题意,由x>0,y≥0,-2n(x-3)≥y≥0得0<x≤3,
所以平面区域为Dn内的整点为点(3,0)与在直线x=1和x=2上的整点,
所以直线y=-2n(x-3)与直线x=1和x=2交点纵坐标分别为y1=4n和y2=2n,
所以Dn内在直线x=1和x=2上的整点个数分别为4n+1和2n+1,所以an=4n+1+2n+1+1=6n+3.
(2)由bn+1=2bn+an,得bn+1=2bn+6n+3,
所以bn+1+6(n+1)+9=2(bn+6n+9),
因为b1+6+9=2,
所以{bn+6n+9}是以2为首项,公比为2的等比数列,所以bn+6n+9=2n,所以bn=2n-6n-9.
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.不等式组的解集为( )
A.{x|-2<x<-1}
B.{x|-1<x<0}
C.{x|0<x<1}
D.{x|x>1}
2.若集合A=,B={x|y=log2[(2-x)(1+x)]},则A∩B=( )
A.[-2,2) B.(-1,1)
C.(-1,1] D.(-1,2)
3.已知M=2a(a-2),N=(a+1)(a-3),则M,N的大小关系是( )
A.M>N B.M≥N
C.M
5.不等式≥1的解集为( )
A.(-∞,-1]∪[2,+∞)
B.(-∞,-1]∪
C.(-∞,-1]∪
D.∪[2,+∞)
6.不等式ax2+bx+2>0的解集是(-,),则a+b的值是( )
A.10 B.-10 C.-14 D.14
7.已知x,y满足约束条件当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2时,a2+b2的最小值为( )
A.5 B.4 C. D.2
8.若一元二次方程x2+(a-1)x+1-a2=0有两个正实数根,则a的取值范围是( )
A.(-1,1)
B.∪[1,+∞)
C.
D.
9.已知x>0,y>0,lg 2x+lg 8y=lg 2,则+的最小值是( )
A.2 B.2 C.4 D.2
10.已知z=2x+y,x,y满足且z的最大值是最小值的4倍,则实数a的值是( )
A. B. C. D.
11.某公司租地建仓库,每月土地费用与仓库到车站距离成反比,而每月货物的运输费用与仓库到车站距离成正比.如果在距离车站10 km处建仓库,则土地费用和运输费用分别为2万元和8万元,那么要使两项费用之和最小,仓库应建在离车站( )
A.5 km处 B.4 km处
C.3 km处 D.2 km处
12.已知-1≤x+y≤4,且2≤x-y≤3,则z=2x-3y的取值范围是( )
A.[3,8] B.[3,6]
C.[6,7] D.[4,5]
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)
13.某小型服装厂生产一种风衣,日销货量x件与货价p元/件之间的关系为p=160-2x,生产x件所需成本为C=500+30x元,则该厂日产量为______时,日获利不少于1 300元.
14.已知a,b,x,y∈(0,+∞),且+=1,x2+y2=8,则ab与xy的大小关系为____.
15.已知实数a,b,c满足a+b+c=0,a2+b2+c2=1,则a的最大值是________.
16.(2020·全国Ⅱ卷)若x,y满足约束条件则z=x+2y的最大值是________.
三、解答题(共70分)
17.(10分)已知实数x,y满足
(1)z=的取值范围;
(2)z=x2+y2-10y+25的最小值.
18.(12分)某厂家拟在2020年举行促销活动,经调查测算,某产品的年销售量(即该厂的年产量)m万件与年促销费用x万元,满足m=3-(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2020年该产品的利润y(万元)表示为年促销费用x(万元)的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
19.(12分)正数x,y满足+=1.
(1)求xy的最小值;
(2)求x+2y的最小值.
20.(12分)某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力及每天资源限额(最大供应量)如表所示:
每吨甲产品 每吨乙产品 每天资源额
煤/t 8 4 320
电力/kW·h 3 4 150
劳动力/个 4 8 280
若生产每吨甲、乙两种产品获得的利润分别为5万元、8万元,问:每天生产甲、乙两种产品各多少吨时,该厂获得最大利润?
21.(12分)已知函数y=的定义域为R.
(1)求a的取值范围;
(2)解关于x的不等式x2-x-a2+a<0.
22.(12分)在平面直角坐标系上,设不等式组(n∈N+)表示的平面区域为Dn,记Dn内的整点(横坐标和纵坐标均为整数的点)的个数为an.
(1)求数列{an}的通项公式.
(2)若bn+1=2bn+an,b1=-13.
求证:数列{bn+6n+9}是等比数列,并求出数列{bn}的通项公式.
答案解析
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.不等式组的解集为( )
A.{x|-2<x<-1}
B.{x|-1<x<0}
C.{x|0<x<1}
D.{x|x>1}
【解析】选C.原不等式组可化为
,解得0<x<1.
2.若集合A=,B={x|y=log2[(2-x)(1+x)]},则A∩B=( )
A.[-2,2) B.(-1,1)
C.(-1,1] D.(-1,2)
【解析】选B.不等式≤0,等价于(x+2)(x-1)≤0且x-1≠0,解得-2≤x<1,即A=.
函数y=log2的定义域为(2-x)(1+x)>0,解得-1
A.M>N B.M≥N
C.M
4.不等式(x-2y+1)(x+y-3)≤0在平面直角坐标系内表示的区域(用阴影部分表示),应是下列图形中的( )
【解析】选C.(x-2y+1)(x+y-3)≤0等价于或
即不等式表示的区域是同时在两直线的上方或同时在两直线的下方,只有C项符合.
5.不等式≥1的解集为( )
A.(-∞,-1]∪[2,+∞)
B.(-∞,-1]∪
C.(-∞,-1]∪
D.∪[2,+∞)
【解析】选D.由题得-1≥0,
所以≥0,所以≥0,
所以
所以-1≤x<或x≥2.即该不等式的解集为∪[2,+∞).
6.不等式ax2+bx+2>0的解集是(-,),则a+b的值是( )
A.10 B.-10 C.-14 D.14
【解析】选C.因为不等式ax2+bx+2>0的解集是,所以方程ax2+bx+2=0的两根为-和.所以所以a+b=-14.
7.已知x,y满足约束条件当目标函数z=ax+by(a>0,b>0)在该约束条件下取到最小值2时,a2+b2的最小值为( )
A.5 B.4 C. D.2
【解析】选B.约束条件满足的可行域如图中的阴影部分所示.由图可知,目标函数z=ax+by(a>0,b>0)取最小值时,最优解为(2,1).
所以2a+b=2,则b=2-2a,
所以a2+b2=a2+(2-2a)2=5a2-8a+20=52+4,即当a=,b=时,a2+b2有最小值4.
8.若一元二次方程x2+(a-1)x+1-a2=0有两个正实数根,则a的取值范围是( )
A.(-1,1)
B.∪[1,+∞)
C.
D.
【解析】选C.因为方程有两个正实数根,不妨设为x1,x2,
所以有
即所以-1<a≤-.
9.已知x>0,y>0,lg 2x+lg 8y=lg 2,则+的最小值是( )
A.2 B.2 C.4 D.2
【解析】选C.由lg 2x+lg 8y=lg 2,得lg 2x+3y=lg 2,所以x+3y=1,+=(+)(x+3y)=2++≥4.
当且仅当即时,等号成立.
故+的最小值是4.
10.已知z=2x+y,x,y满足且z的最大值是最小值的4倍,则实数a的值是( )
A. B. C. D.
【解析】选B.在坐标平面内画出题中的不等式组表示的平面区域(图略)及直线2x+y=0,平移该直线,当相应直线分别经过该平面区域内的点(a,a)与(1,1)时,相应直线在y轴上的截距达到最小与最大,此时z=2x+y取得最小值与最大值,于是有2×1+1=4(2a+a),a=.
11.某公司租地建仓库,每月土地费用与仓库到车站距离成反比,而每月货物的运输费用与仓库到车站距离成正比.如果在距离车站10 km处建仓库,则土地费用和运输费用分别为2万元和8万元,那么要使两项费用之和最小,仓库应建在离车站( )
A.5 km处 B.4 km处
C.3 km处 D.2 km处
【解析】选A.设车站到仓库距离为x km(x>0),土地费用为y1万元,运输费用为y2万元,由题意得y1=,y2=k2x,
因为x=10时,y1=2,y2=8,
所以k1=20,k2=,所以费用之和为y=y1+y2=+x≥2=8,当且仅当=,即x=5时取等号.
12.已知-1≤x+y≤4,且2≤x-y≤3,则z=2x-3y的取值范围是( )
A.[3,8] B.[3,6]
C.[6,7] D.[4,5]
【解析】(方法一)
选A.作出不等式组表示的可行域,如图中阴影部分(含边界)所示.
在可行域内平移直线2x-3y=0,当直线经过x-y=2与x+y=4的交点A(3,1)时,目标函数有最小值,zmin=2×3-3×1=3;当直线经过x+y=-1与x-y=3的交点B(1,-2)时,目标函数有最大值,zmax=2×1+3×2=8.所以z∈[3,8].
(方法二)选A.设2x-3y=λ(x+y)+μ(x-y),则(λ+μ)x+(λ-μ)y=2x-3y,
所以解得
所以z=-(x+y)+(x-y).
因为-1≤x+y≤4,所以-2≤-(x+y)≤.①
因为2≤x-y≤3,所以5≤(x-y)≤.②
①+②得,3≤-(x+y)+(x-y)≤8,
所以z的取值范围是[3,8].
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)
13.某小型服装厂生产一种风衣,日销货量x件与货价p元/件之间的关系为p=160-2x,生产x件所需成本为C=500+30x元,则该厂日产量为______时,日获利不少于1 300元.
【解析】由题意,得(160-2x)x-(500+30x)≥1 300,化简得x2-65x+900≤0,解得20≤x≤45.因此,该厂日产量为20件至45件时,日获利不少于1 300元.
答案:20件至45件
14.已知a,b,x,y∈(0,+∞),且+=1,x2+y2=8,则ab与xy的大小关系为____.
【解析】因为1=+≥2=,所以ab≥4.因为8=x2+y2≥2xy,所以xy≤4.所以ab≥4≥xy.
答案:ab≥xy
15.已知实数a,b,c满足a+b+c=0,a2+b2+c2=1,则a的最大值是________.
【解析】因为a+b+c=0,所以b+c=-a.
因为a2+b2+c2=1,所以-a2+1=b2+c2=(b+c)2-2bc=a2-2bc,所以2a2-1=2bc≤b2+c2=1-a2,所以3a2≤2,所以a2≤,所以-≤a≤.所以amax=.
答案:
16.(2020·全国Ⅱ卷)若x,y满足约束条件则z=x+2y的最大值是________.
【解析】不等式组表示的平面区域如图阴影部分(含边界)所示:
平移直线y=-x,当直线经过点A时,直线y=-x+z在纵轴上的截距最大,此时点A的坐标是方程组的解,
解得:
因此z=x+2y的最大值为2+2×3=8.
答案:8
三、解答题(共70分)
17.(10分)已知实数x,y满足
(1)z=的取值范围;
(2)z=x2+y2-10y+25的最小值.
【解析】作出可行域如图所示,并求出各点的坐标为A(1,3),B(3,1),C(7,9),Q(-1,-).
(1)将z=变形为z=2×,由斜率公式可知表示可行域内任一点(x,y)与定点Q连线的斜率的两倍,
因此kQ A==,kQB==,故z的范围为.
(2)z=x2+y2-10y+25=x2+(y-5)2表示可行域内任一点(x,y)到定点M(0,5)的距离的平方,
过M作直线AC的垂线,易知垂足N在线段AC上,M(0,5),直线AC:x-y+2=0,
故由点到直线距离公式可得|MN|==,
所以z的最小值是|MN|2=.
18.(12分)某厂家拟在2020年举行促销活动,经调查测算,某产品的年销售量(即该厂的年产量)m万件与年促销费用x万元,满足m=3-(k为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2020年该产品的利润y(万元)表示为年促销费用x(万元)的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
【解析】(1)由题意知,当x=0时,m=1,
所以1=3-k,k=2,m=3-,
每件产品的销售价格为1.5×元.
所以2020年的利润y=1.5×·m-8-16m-x=--x+28(x≥0).
(2)由(1)知,y=--x+28=--(x+1)+29 =-+29≤
-2+29=21,
当且仅当=(x+1),即x=3时取等号,该厂家2020年的促销费用投入3万元时,厂家的利润最大,为21万元.
19.(12分)正数x,y满足+=1.
(1)求xy的最小值;
(2)求x+2y的最小值.
【解析】(1)由1=+≥2得xy≥36,当且仅当=,即y=9x=18时取等号,故xy的最小值为36.
(2)由题意可得x+2y=(x+2y)(+)=19++≥19+2=19+6,当且仅当=,即9x2=2y2时取等号,故x+2y的最小值为19+6.
20.(12分)某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力及每天资源限额(最大供应量)如表所示:
每吨甲产品 每吨乙产品 每天资源额
煤/t 8 4 320
电力/kW·h 3 4 150
劳动力/个 4 8 280
若生产每吨甲、乙两种产品获得的利润分别为5万元、8万元,问:每天生产甲、乙两种产品各多少吨时,该厂获得最大利润?
【解析】设此工厂每天分别生产甲、乙两种产品x吨,y吨,获得利润z万元,
依题意可得约束条件
作出可行域,如图阴影部分所示.
利润目标函数z=5x+8y.
由几何意义知,当直线y=-x+z经过可行域上的点M时,z=5x+8y取最大值.
解方程组得
即M(10,30).所以每天生产甲种产品10吨,乙种产品30吨时,该厂获得最大利润.
21.(12分)已知函数y=的定义域为R.
(1)求a的取值范围;
(2)解关于x的不等式x2-x-a2+a<0.
【解析】(1)因为函数y=的定义域为R,
所以ax2+2ax+1≥0,恒成立.
①当a=0时,1≥0恒成立;
②当a≠0时,则
解得0<a≤1.
综上,a的取值范围为[0,1].
(2)由x2-x-a2+a<0得,(x-a)[x-(1-a)]<0.
因为0≤a≤1,所以①当1-a>a,
即0≤a<时,a<x<1-a;
②当1-a=a,即a=时,<0,不等式无解;
③当1-a<a,即<a≤1时1-a<x<a.
综上所述,当0≤a<时,解集为(a,1-a);
当a=时,解集为;当<a≤1时,解集为(1-a,a).
22.(12分)在平面直角坐标系上,设不等式组(n∈N+)表示的平面区域为Dn,记Dn内的整点(横坐标和纵坐标均为整数的点)的个数为an.
(1)求数列{an}的通项公式.
(2)若bn+1=2bn+an,b1=-13.
求证:数列{bn+6n+9}是等比数列,并求出数列{bn}的通项公式.
【解析】(1)根据题意,由x>0,y≥0,-2n(x-3)≥y≥0得0<x≤3,
所以平面区域为Dn内的整点为点(3,0)与在直线x=1和x=2上的整点,
所以直线y=-2n(x-3)与直线x=1和x=2交点纵坐标分别为y1=4n和y2=2n,
所以Dn内在直线x=1和x=2上的整点个数分别为4n+1和2n+1,所以an=4n+1+2n+1+1=6n+3.
(2)由bn+1=2bn+an,得bn+1=2bn+6n+3,
所以bn+1+6(n+1)+9=2(bn+6n+9),
因为b1+6+9=2,
所以{bn+6n+9}是以2为首项,公比为2的等比数列,所以bn+6n+9=2n,所以bn=2n-6n-9.
