2021-2022学年湖南省娄底市双峰县九年级(上)期末数学试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年湖南省娄底市双峰县九年级(上)期末数学试卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 10:36:18 | ||
图片预览


文档简介
2021-2022学年湖南省娄底市双峰县九年级第一学期期末数学试卷
一、选择题(本大题共12小题,满分36分,每小题给出的四个选项中,只有一项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方框里)
1.已知反比例函数y=﹣,这个函数的比例系数和自变量的取值范围是( )
A.k=﹣8;x≠0 B.k=﹣8;x>0 C.k=0;x>0 D.k=8;x≠0
2.将一元二次方程2x2+3x=1化成一般形式时,它的二次项、一次项系数和常数项分别为( )
A.2x2,﹣3,1 B.2x2,3,﹣1 C.﹣2x2,﹣3,﹣1 D.﹣2x2,3,1
3.一元二次方程x2﹣4x﹣1=0配方后可化为( )
A.(x+2)2=3 B.(x+2)2=5 C.(x﹣2)2=3 D.( x﹣2)2=5
4.将一块长方形桌布铺在长为3m、宽为2m的长方形桌面上,各边下垂的长度相同,并且桌布的面积是桌面面积的2倍,那么桌布下垂的长度为( )
A.﹣2.5 B.2.5 C.0.5 D.﹣0.5
5.若a:b=3:4,且a+b=14,则2a﹣b的值是( )
A.4 B.2 C.20 D.14
6.如图,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③=; ④AC2=AD AB.其中能够单独判定△ABC∽△ACD的条件个数为( )
A.1 B.2 C.3 D.4
7.如图所示,在△ABC中,点D,E分别在AB,AC上,并且DE∥BC,,△ADE的面积为8,则△ABC的面积为( )
A.12 B.13 C.16 D.18
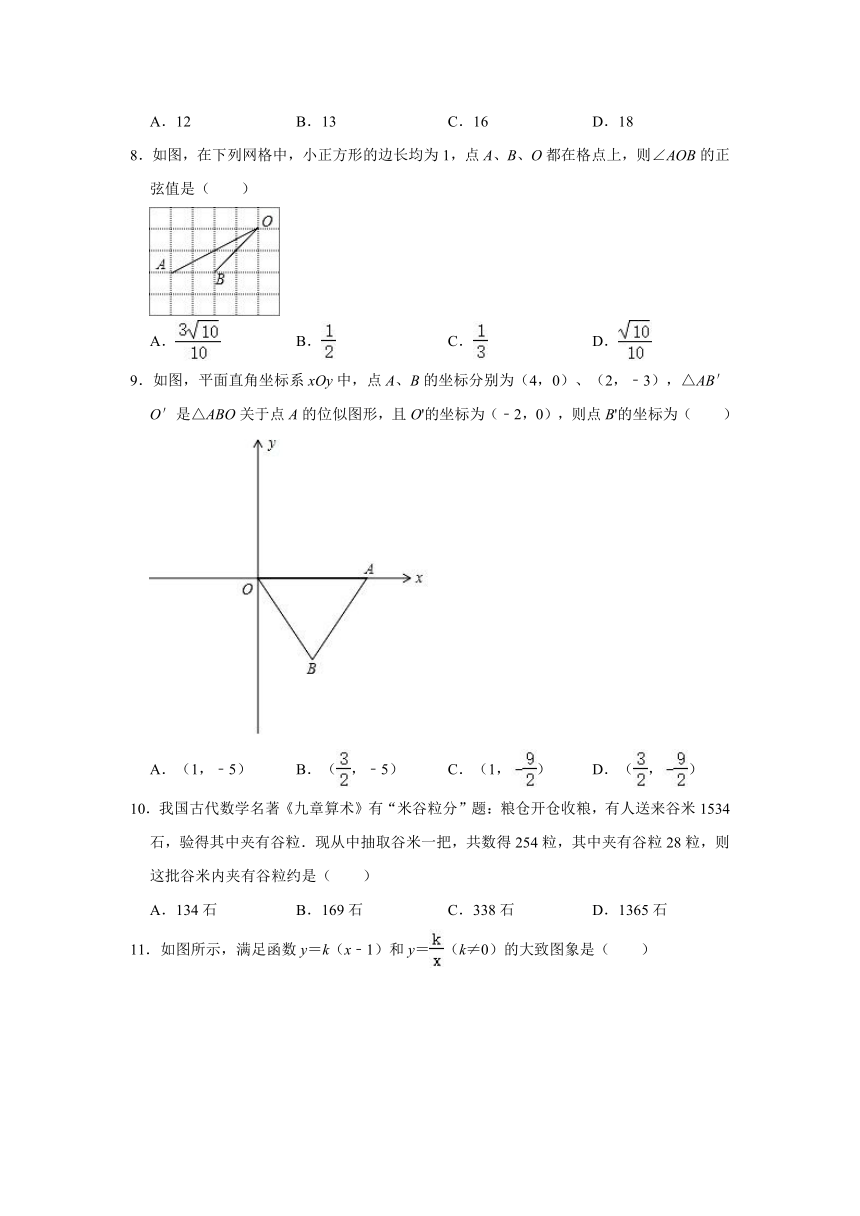
8.如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A. B. C. D.
9.如图,平面直角坐标系xOy中,点A、B的坐标分别为(4,0)、(2,﹣3),△AB′O′是△ABO关于点A的位似图形,且O'的坐标为(﹣2,0),则点B'的坐标为( )
A.(1,﹣5) B.(,﹣5) C.(1,) D.(,)
10.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来谷米1534石,验得其中夹有谷粒.现从中抽取谷米一把,共数得254粒,其中夹有谷粒28粒,则这批谷米内夹有谷粒约是( )
A.134石 B.169石 C.338石 D.1365石
11.如图所示,满足函数y=k(x﹣1)和y=(k≠0)的大致图象是( )
A.①② B.②③ C.②④ D.①④
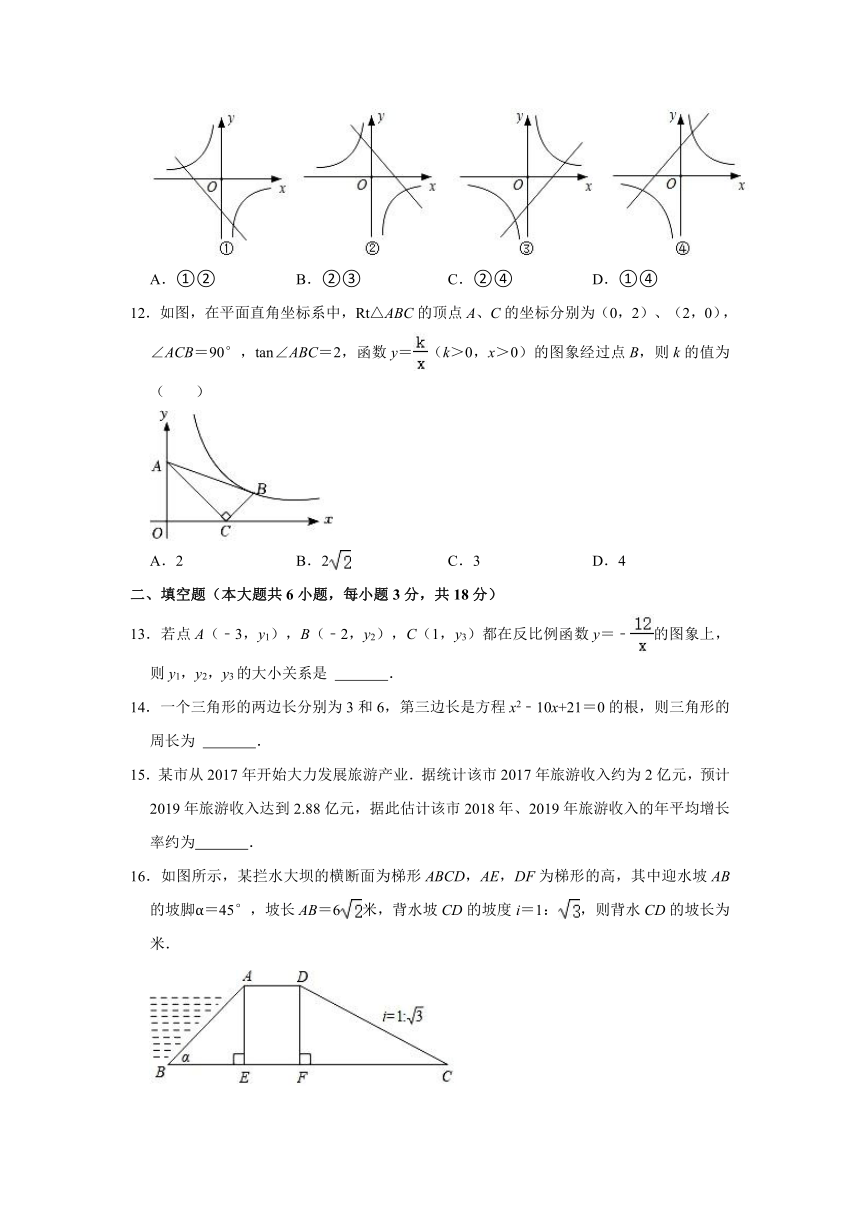
12.如图,在平面直角坐标系中,Rt△ABC的顶点A、C的坐标分别为(0,2)、(2,0),∠ACB=90°,tan∠ABC=2,函数y=(k>0,x>0)的图象经过点B,则k的值为( )
A.2 B.2 C.3 D.4
二、填空题(本大题共6小题,每小题3分,共18分)
13.若点A(﹣3,y1),B(﹣2,y2),C(1,y3)都在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是 .
14.一个三角形的两边长分别为3和6,第三边长是方程x2﹣10x+21=0的根,则三角形的周长为 .
15.某市从2017年开始大力发展旅游产业.据统计该市2017年旅游收入约为2亿元,预计2019年旅游收入达到2.88亿元,据此估计该市2018年、2019年旅游收入的年平均增长率约为 .
16.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡脚α=45°,坡长AB=6米,背水坡CD的坡度i=1:,则背水CD的坡长为 米.
17.若△ABC∽△A′B′C′,且,△ABC的周长为12cm,则△A′B′C′的周长为 cm.
18.如图,点A1,A2,A3…在反比例函数y=(x>0)的图象上,点B1,B2,B3,…,Bn在y轴上,且∠B1OA1=∠B2B1A2=∠B3B2A3=…,直线y=x与双曲线y=交于点A1,B1A1⊥OA1,B2A2⊥B1A2,B3A3⊥B2A3,…,则B2022的坐标是 .
三、解答题(本大题共2小题,每小题6分,满分12分)
19.计算:2cos245°﹣﹣(sin60°﹣1)0+.
20.已知:平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+﹣=0的两个实数根.
(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么 ABCD的周长是多少?
四、解答题(本大题共2小题,每小题8分,满分16分)
21.争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分)
78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93
整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) 频数
78≤x<82 5
82≤x<86 a
86≤x<90 11
90≤x<94 b
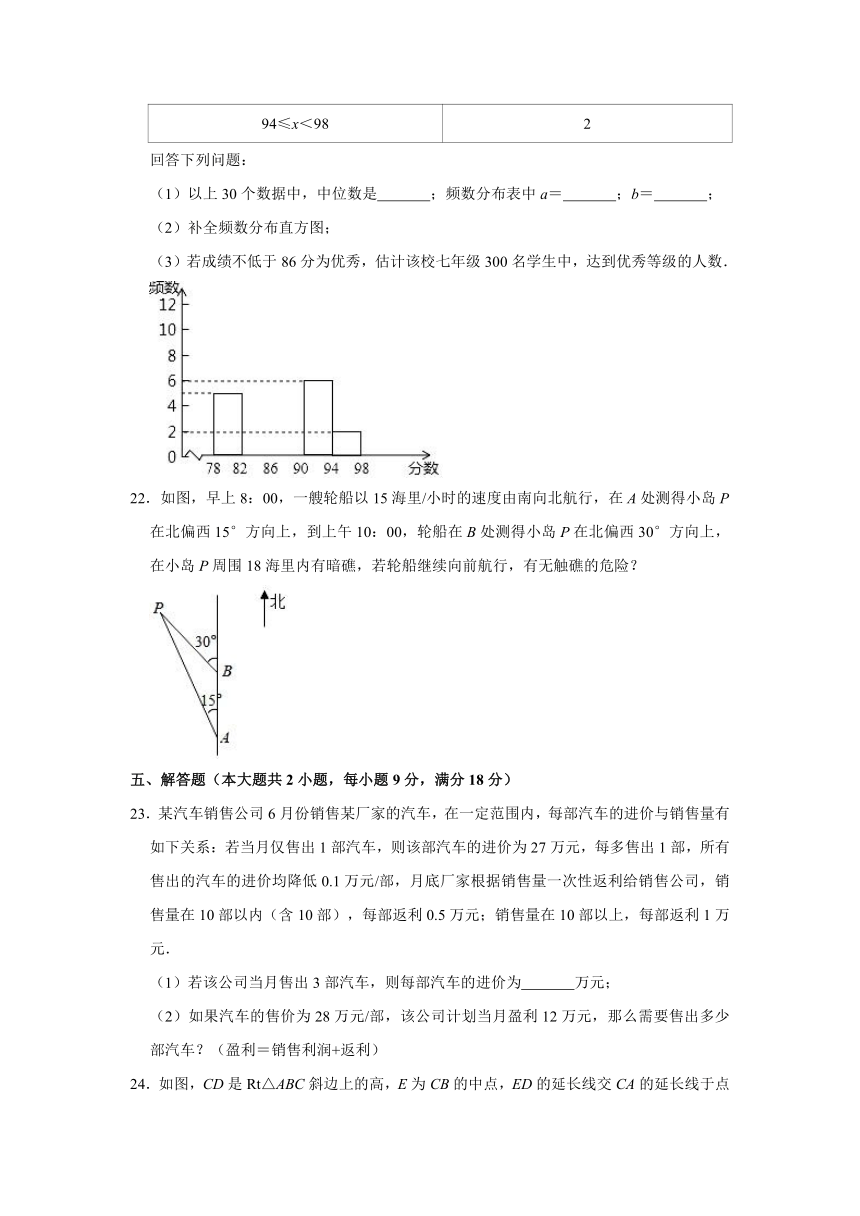
94≤x<98 2
回答下列问题:
(1)以上30个数据中,中位数是 ;频数分布表中a= ;b= ;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.
22.如图,早上8:00,一艘轮船以15海里/小时的速度由南向北航行,在A处测得小岛P在北偏西15°方向上,到上午10:00,轮船在B处测得小岛P在北偏西30°方向上,在小岛P周围18海里内有暗礁,若轮船继续向前航行,有无触礁的危险?
五、解答题(本大题共2小题,每小题9分,满分18分)
23.某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,月底厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元;销售量在10部以上,每部返利1万元.
(1)若该公司当月售出3部汽车,则每部汽车的进价为 万元;
(2)如果汽车的售价为28万元/部,该公司计划当月盈利12万元,那么需要售出多少部汽车?(盈利=销售利润+返利)
24.如图,CD是Rt△ABC斜边上的高,E为CB的中点,ED的延长线交CA的延长线于点F.求证:AC CF=CB DF.
六、解答题(本大题共2小题,每小题10分,满分20分)
25.如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)若M(x1,y1)、N(x2,y2)是反比例函数y=上的两点,当x1<x2<0时,比较y2与y1的大小关系.
26.如图,矩形ABCD中,已知AB=6.BC=8,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F.将△ABE沿直线AE翻折,点B的对应点为点B'.
(1)如图1,若点E为线段BC上一点,延长AB'交CD于点M,求证:AM=FM;
(2)如图2,若点B'恰好落在对角线AC上,求的值;
(3)若=,求∠DAB'的正弦值.
参考答案
一、选择题(本大题共12小题,满分36分,每小题给出的四个选项中,只有一项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方框里)
1.已知反比例函数y=﹣,这个函数的比例系数和自变量的取值范围是( )
A.k=﹣8;x≠0 B.k=﹣8;x>0 C.k=0;x>0 D.k=8;x≠0
【分析】反比例函数k的值就是比例系数,x在分母上,因此x≠0.
解:反比例函数k的值为:k=﹣8,自变量x的取值范围为x≠0,
故选:A.
2.将一元二次方程2x2+3x=1化成一般形式时,它的二次项、一次项系数和常数项分别为( )
A.2x2,﹣3,1 B.2x2,3,﹣1 C.﹣2x2,﹣3,﹣1 D.﹣2x2,3,1
【分析】根据一元二次方程的一般形式,ax2+bx+c=0(a,b,c是常数,a≠0)判断即可.
解:将一元二次方程2x2+3x=1化成一般形式为:2x2+3x﹣1=0,
∴它的二次项、一次项系数和常数项分别为:2x2,3,﹣1,
故选:B.
3.一元二次方程x2﹣4x﹣1=0配方后可化为( )
A.(x+2)2=3 B.(x+2)2=5 C.(x﹣2)2=3 D.( x﹣2)2=5
【分析】移项,配方,即可得出选项.
解:x2﹣4x﹣1=0,
x2﹣4x=1,
x2﹣4x+4=1+4,
(x﹣2)2=5,
故选:D.
4.将一块长方形桌布铺在长为3m、宽为2m的长方形桌面上,各边下垂的长度相同,并且桌布的面积是桌面面积的2倍,那么桌布下垂的长度为( )
A.﹣2.5 B.2.5 C.0.5 D.﹣0.5
【分析】设桌布铺到桌面上时各边垂下的长度为xm,则用含x的代数式表示桌布的长为(3+2x)m,宽为(2+2x)m,依题意得(2x+3)(2x+2)=2×3×2,列方程即可得到结论.
解:设桌布铺到桌面上时各边垂下的长度为xm,则桌布的长为(3+2x)m,宽为(2+2x)m,
依题意得(2x+3)(2x+2)=2×3×2,
解得x1=0.5,x2=﹣3(舍去),
答:桌布下垂的长度为0.5m,
故选:C.
5.若a:b=3:4,且a+b=14,则2a﹣b的值是( )
A.4 B.2 C.20 D.14
【分析】根据比例的性质得到3b=4a,结合a+b=14求得a、b的值,代入求值即可.
解:由a:b=3:4知3b=4a,
所以b=.
所以由a+b=14得到:a+=14,
解得a=6.
所以b=8.
所以2a﹣b=2×6﹣8=4.
故选:A.
6.如图,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③=; ④AC2=AD AB.其中能够单独判定△ABC∽△ACD的条件个数为( )
A.1 B.2 C.3 D.4
【分析】由图可知△ABC与△ACD中∠A为公共角,所以只要再找一组角相等,或一组对应边成比例即可解答.
解:有三个.
①∠B=∠ACD,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
②∠ADC=∠ACB,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
③中∠A不是已知的比例线段的夹角,不正确
④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定;
故选:C.
7.如图所示,在△ABC中,点D,E分别在AB,AC上,并且DE∥BC,,△ADE的面积为8,则△ABC的面积为( )
A.12 B.13 C.16 D.18
【分析】由DE∥BC可得△ADE∽△ABC,由可求得△ADE与△ABC的面积比为4:9,再由△ADE的面积为8,即可求出答案.
解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∵,
∴,
∵△ADE的面积为8,
∴,
∴△ABC的面积为18,
故选:D.
8.如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A. B. C. D.
【分析】取格点C,连接AC,BC,观察图象可知,O,B,C共线,∠ACO=90°,利用勾股定理求得AC和AO的长,根据正弦的定义即可求解.
解:取格点C,连接AC,BC,观察图象可知,O,B,C共线,∠ACO=90°,
∵AC=,AO===2,
∴sin∠AOB===.
故选:D.
9.如图,平面直角坐标系xOy中,点A、B的坐标分别为(4,0)、(2,﹣3),△AB′O′是△ABO关于点A的位似图形,且O'的坐标为(﹣2,0),则点B'的坐标为( )
A.(1,﹣5) B.(,﹣5) C.(1,) D.(,)
【分析】过点B作BE⊥x轴于点E,B′作B′F⊥x轴于点F,根据位似变换的性质得到==,根据相似三角形的性质列出比例式,计算即可.
解:过点B作BE⊥x轴于点E,B′作B′F⊥x轴于点F,
则BE∥B′F,
由题意得,OE=EA=2,BE=3,
∵点A、B的坐标分别为(4,0)、(2,﹣3),△AB′O′是△ABO关于的A的位似图形,且O′的坐标为(﹣2,0),
∴OB∥O′B′,
∴===,
∵BE∥B′F,
∴△AEB∽△AFB′,
∴===,即==,
解得,AF=3,B′F=,
∴OF=1,
则点B'的坐标为(1,﹣),
故选:C.
10.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来谷米1534石,验得其中夹有谷粒.现从中抽取谷米一把,共数得254粒,其中夹有谷粒28粒,则这批谷米内夹有谷粒约是( )
A.134石 B.169石 C.338石 D.1365石
【分析】根据254粒内夹谷28粒,可得比例,再乘以1534石,即可得出答案.
解:根据题意得:
1534×≈169(石),
答:这批谷米内夹有谷粒约169石;
故选:B.
11.如图所示,满足函数y=k(x﹣1)和y=(k≠0)的大致图象是( )
A.①② B.②③ C.②④ D.①④
【分析】分别根据一次函数与反比例函数图象的特点解答即可.
解:∵y=k(x﹣1),
∴函数y=k(x﹣1)过点(1,0),
故①④不合题意;
当k>0时,函数y=k(x﹣1)过第一、三、四象限,函数y=(k≠0)在一、三象限;
当k<0时,函数y=k(x﹣1)过第一、二、四象限,函数y=(k≠0)在二、四象限;
故②③符合题意;
故选:B.
12.如图,在平面直角坐标系中,Rt△ABC的顶点A、C的坐标分别为(0,2)、(2,0),∠ACB=90°,tan∠ABC=2,函数y=(k>0,x>0)的图象经过点B,则k的值为( )
A.2 B.2 C.3 D.4
【分析】过B点作BD⊥x轴于D,如图,先关键勾股定理得到AC=2,∠ACO=45°,再判断△BCD为等腰直角三角形得到CD=BD=BC,则可计算出CD=BD=1,所以B(3,1),然后利用反比例函数图象上点的坐标特征求出k的值.
解:过点B作BD⊥x轴,垂足为D,
∵点A、C的坐标分别为(0,2)、(2,0),
∴OA=OC=2,
在Rt△AOC中,AC===2,
又∵tan∠ABC=2,
∴tan∠ABC==2,
∴BC=AC=,
又∵∠ACB=90°,
∴∠OAC=∠OCA=45°=∠BCD=∠CBD,
∴CD=BD=BC=×=1,
∴OD=2+1=3,
∴B(3,1),
将点B的坐标代入y=得:k=3,
故选:C.
二、填空题(本大题共6小题,每小题3分,共18分)
13.若点A(﹣3,y1),B(﹣2,y2),C(1,y3)都在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是 y3<y1<y2 .
【分析】先根据函数解析式中的比例系数k确定函数图象所在的象限,再根据各象限内点的坐标特点及函数的增减性解答.
解:∵在反比例函数y=﹣中,k=﹣12<0,
∴此函数图象在第二、四象限,在每个象限内y随x增大而增大,
∵﹣3<﹣2<0,
∴点A(﹣3,y1),B(﹣2,y2)在第二象限,
∴0<y1<y2.
∵1>0,
∴C(1,y3)点在第四象限,
∴y3<0,
∴y3<y1<y2.
故答案为:y3<y1<y2.
14.一个三角形的两边长分别为3和6,第三边长是方程x2﹣10x+21=0的根,则三角形的周长为 16 .
【分析】首先求出方程的根,再根据三角形三边关系定理,确定第三边的长,进而求其周长.
解:解方程x2﹣10x+21=0得x1=3、x2=7,
∵3<第三边的边长<9,
∴第三边的边长为7.
∴这个三角形的周长是3+6+7=16.
故答案为:16.
15.某市从2017年开始大力发展旅游产业.据统计该市2017年旅游收入约为2亿元,预计2019年旅游收入达到2.88亿元,据此估计该市2018年、2019年旅游收入的年平均增长率约为 20% .
【分析】设该市2018年、2019年旅游收入的年平均增长率为x,根据该市2017年及2019年的旅游收入,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
解:设该市2018年、2019年旅游收入的年平均增长率为x,
依题意,得:2(1+x)2=2.88,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
故答案为:20%.
16.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡脚α=45°,坡长AB=6米,背水坡CD的坡度i=1:,则背水CD的坡长为 12 米.
【分析】根据正弦的定义求出AE,进而求出DF,根据坡度的概念求出FC,根据勾股定理计算,得到答案.
解:由题意可知,四边形AEFD为矩形,
∴DF=AE,
在Rt△ABE中,∠B=45°,AB=6米,
则AE=AB sinB=6×=6(米),
∴DF=6米,
∵背水坡CD的坡度i=1:,
∴FC=6米,
∴CD===12(米),
故答案为:12.
17.若△ABC∽△A′B′C′,且,△ABC的周长为12cm,则△A′B′C′的周长为 16 cm.
【分析】根据相似三角形周长的比等于相似比求解.
解:∵△ABC∽△A′B′C′,且,即相似三角形的相似比是
∵△ABC的周长为12cm
∴△A′B′C′的周长为12÷=16cm.
18.如图,点A1,A2,A3…在反比例函数y=(x>0)的图象上,点B1,B2,B3,…,Bn在y轴上,且∠B1OA1=∠B2B1A2=∠B3B2A3=…,直线y=x与双曲线y=交于点A1,B1A1⊥OA1,B2A2⊥B1A2,B3A3⊥B2A3,…,则B2022的坐标是 (0,2) .
【分析】由题意,△OA1B1,△B1A2B2,△B2A3B3,…,都是等腰直角三角形,想办法求出OB1,OB2,OB3,OB4,…,探究规律,利用规律解决问题即可得出结论.
解:由题意,△OA1B1,△B1A2B2,△B2A3B3,…,都是等腰直角三角形,
∵A1(1,1),
∴OB1=2,设A2(m,2+m),
则有m(2+m)=1,
解得m=﹣1,
∴OB2=2,
设A3(a,2+a),则有a(2+a)=1,
解得a=﹣,
∴OB3=2,
同法可得,OB4=2,
∴OBn=2,
∴Bn(0,2),
∴B2022(0,2),
故答案为:.
三、解答题(本大题共2小题,每小题6分,满分12分)
19.计算:2cos245°﹣﹣(sin60°﹣1)0+.
【分析】将特殊角的三角函数值代入,然后进行负整数指数幂的运算,将各部分化为最简后合并即可得出答案.
解:原式=2×()2﹣|2﹣|﹣1+4
=1﹣(2﹣)﹣1+4
=+2.
20.已知:平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+﹣=0的两个实数根.
(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么 ABCD的周长是多少?
【分析】(1)根据菱形的性质可得出AB=AD,结合根的判别式,即可得出关于m的一元二次方程,解之即可得出m的值,将其代入原方程,解之即可得出菱形的边长;
(2)将x=2代入原方程可求出m的值,将m的值代入原方程结合根与系数的关系可求出方程的另一根AD的长,再根据平行四边形的周长公式即可求出 ABCD的周长.
解:(1)∵四边形ABCD是菱形,
∴AB=AD.
又∵AB、AD的长是关于x的方程x2﹣mx+﹣=0的两个实数根,
∴Δ=(﹣m)2﹣4×(﹣)=(m﹣1)2=0,
∴m=1,
∴当m为1时,四边形ABCD是菱形.
当m=1时,原方程为x2﹣x+=0,即(x﹣)2=0,
解得:x1=x2=,
∴菱形ABCD的边长是.
(2)把x=2代入原方程,得:4﹣2m+﹣=0,
解得:m=.
将m=代入原方程,得:x2﹣x+1=0,
∴方程的另一根AD=1÷2=,
∴ ABCD的周长是2×(2+)=5.
四、解答题(本大题共2小题,每小题8分,满分16分)
21.争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分)
78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93
整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) 频数
78≤x<82 5
82≤x<86 a
86≤x<90 11
90≤x<94 b
94≤x<98 2
回答下列问题:
(1)以上30个数据中,中位数是 86 ;频数分布表中a= 6 ;b= 6 ;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.
【分析】(1)将各数按照从小到大顺序排列,找出中位数,根据统计图与表格确定出a与b的值即可;
(2)补全直方图即可;
(3)求出样本中游戏学生的百分比,乘以300即可得到结果.
解:(1)根据题意排列得:78,81,81,81,81,83,83,84,84,85,85,86,86,86,86,86,86,88,89,89,89,89,90,92,92,93,93,93,94,97,可得中位数为86,频数分布表中a=6,b=6;
故答案为:86;6;6;
(2)补全频数分布直方图,如图所示:
(3)根据题意得:300×=190(人),
则该校七年级300名学生中,达到优秀等级的人数估计为190人.
22.如图,早上8:00,一艘轮船以15海里/小时的速度由南向北航行,在A处测得小岛P在北偏西15°方向上,到上午10:00,轮船在B处测得小岛P在北偏西30°方向上,在小岛P周围18海里内有暗礁,若轮船继续向前航行,有无触礁的危险?
【分析】过点P作PD⊥AC于点D,利用三角形外角可求出∠P,利用角的度数可判断△PAB为等腰三角形,利用时间和速度可求出AB的长度,也就求出PB的长,再利用PD=即可求得PD的长度,与18比较即可得出结论.
解:如图,过点P作PD⊥AC于点D,
∵∠PAB=15°,∠PBD=30°,
∴∠APB=15°,
∴∠PAB=∠APB,
∴PB=AB,
∵AB=15×2=30(海里),
∴PB==30(海里),
在Rt△PBD中,∠PDB=90°,∠PBD=30°,
∴PD==30=15<18,
∴轮船继续向前航行,有触礁的危险.
五、解答题(本大题共2小题,每小题9分,满分18分)
23.某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,月底厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元;销售量在10部以上,每部返利1万元.
(1)若该公司当月售出3部汽车,则每部汽车的进价为 26.8 万元;
(2)如果汽车的售价为28万元/部,该公司计划当月盈利12万元,那么需要售出多少部汽车?(盈利=销售利润+返利)
【分析】(1)根据若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,得出该公司当月售出3部汽车时,则每部汽车的进价为:27﹣0.1×2,即可得出答案;
(2)利用设需要售出x部汽车,由题意可知,每部汽车的销售利润,根据当0≤x≤10,以及当x>10时,分别讨论得出即可.
解:(1)∵若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,
∴若该公司当月售出3部汽车,则每部汽车的进价为:27﹣0.1×(3﹣1)=26.8,
故答案为:26.8;
(2)设需要售出x部汽车,
由题意可知,每部汽车的销售利润为:
28﹣[27﹣0.1(x﹣1)]=(0.1x+0.9)(万元),
当0≤x≤10,
根据题意,得x (0.1x+0.9)+0.5x=12,
整理,得x2+14x﹣120=0,
解这个方程,得x1=﹣20(不合题意,舍去),x2=6,
当x>10时,
根据题意,得x (0.1x+0.9)+x=12,
整理,得x2+19x﹣120=0,
解这个方程,得x1=﹣24(不合题意,舍去),x2=5,
因为5<10,所以x2=5舍去.
答:需要售出6部汽车.
24.如图,CD是Rt△ABC斜边上的高,E为CB的中点,ED的延长线交CA的延长线于点F.求证:AC CF=CB DF.
【分析】先证明△FDA∽△FCD,得出,再证明△ACD∽△CBD,可得,即可解答.
【解答】证明:∵CD⊥AB,
∴∠ADC=∠CDB=90°,
∵E为CB的中点,
∴CE=EB=DE=BC,
∴∠B=∠BDE,
∵∠BDE=∠ADF,
∴∠B=∠ADF,
∵∠ACB=90°,
∴∠B+∠CAB=90°,
∵∠ACD+∠CAB=90°
∴∠B=∠ACD,
∴∠ADF=∠ACD,
又∵∠F=∠F,
∴△FDA∽△FCD,
∴,
∵∠ADC=∠CDB=90°,∠ACD=∠B,
∴△ACD∽△CBD,
∴,
∴,
即AC CF=CB DF.
六、解答题(本大题共2小题,每小题10分,满分20分)
25.如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)若M(x1,y1)、N(x2,y2)是反比例函数y=上的两点,当x1<x2<0时,比较y2与y1的大小关系.
【分析】(1)利用待定系数法即可解决求问题.
(2)根据对称性求出点D坐标,发现BD∥x轴,利用三角形的面积公式计算即可.
(3)利用反比例函数的增减性解决问题即可.
解:(1)∵反比例函数y=经过点B(2,﹣1),
∴m=﹣2,
∵点A(﹣1,n)在y=上,
∴n=2,
∴A(﹣1,2),
把A,B坐标代入y=kx+b,则有,
解得,
∴一次函数的解析式为y=﹣x+1,反比例函数的解析式为y=﹣.
(2)∵直线y=﹣x+1交y轴于C,
∴C(0,1),
∵D,C关于x轴对称,
∴D(0,﹣1),∵B(2,﹣1)
∴BD∥x轴,
∴S△ABD=×2×3=3.
(3)∵M(x1,y1)、N(x2,y2)是反比例函数y=﹣上的两点,且x1<x2<0,
∴y1<y2.
26.如图,矩形ABCD中,已知AB=6.BC=8,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F.将△ABE沿直线AE翻折,点B的对应点为点B'.
(1)如图1,若点E为线段BC上一点,延长AB'交CD于点M,求证:AM=FM;
(2)如图2,若点B'恰好落在对角线AC上,求的值;
(3)若=,求∠DAB'的正弦值.
【分析】(1)由折叠的性质及等腰三角形的判定可得出答案;
(2)由勾股定理求出AC=10,证明△ABE∽△FCE,由比例线段可得出答案;
(3)①点E在线段BC上,设DM=x,根据Rt△ADM中,AM2=AD2+DM2,得到关于x的方程,求得x的值,最后根据sin∠DAB'=进行计算即可;②当点E在线段BC的延长线上时,设DM=x,得出(2+x)2=82+x2,求出x=15.则AM=17,可得出答案.
【解答】(1)证明:∵四边形ABCD为矩形,
∴AB∥CD,
∴∠F=∠BAF,
由折叠可知:∠BAF=∠MAF,
∴∠F=∠MAF,
∴AM=FM.
(2)解:同(1)的证法可得△ACF是等腰三角形,AC=CF,
在Rt△ABC中,∵AB=6,BC=8,
∴AC===10,
∴CF=AC=10,
∵AB∥CF,
∴△ABE∽△FCE,
∴;
(3)①当点E在线段BC上时,如图3,AB'的延长线交CD于点M,
由AB∥CF可得:△ABE∽△FCE,
∴,即,
∴CF=4,
同(1)的证法可得AM=FM.
设DM=x,则MC=6﹣x,则AM=FM=10﹣x,
在Rt△ADM中,AM2=AD2+DM2,即(10﹣x)2=82+x2,
解得:x=,
则AM=10﹣x=10﹣=,
∴sin∠DAB'==.
②当点E在线段BC的延长线上时,如图4,
由AB∥CF可得:△ABE∽△FCE,
∴,即,
∴CF=4,
则DF=6﹣4=2,
设DM=x,同理可得出AM=FM=2+x,
∵AM2=AD2+DM2,
∴(2+x)2=82+x2,
解得x=15.
∴AM=17,
∴sin∠DAB'=.
综合以上可得,∠DAB'的正弦值为或.
一、选择题(本大题共12小题,满分36分,每小题给出的四个选项中,只有一项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方框里)
1.已知反比例函数y=﹣,这个函数的比例系数和自变量的取值范围是( )
A.k=﹣8;x≠0 B.k=﹣8;x>0 C.k=0;x>0 D.k=8;x≠0
2.将一元二次方程2x2+3x=1化成一般形式时,它的二次项、一次项系数和常数项分别为( )
A.2x2,﹣3,1 B.2x2,3,﹣1 C.﹣2x2,﹣3,﹣1 D.﹣2x2,3,1
3.一元二次方程x2﹣4x﹣1=0配方后可化为( )
A.(x+2)2=3 B.(x+2)2=5 C.(x﹣2)2=3 D.( x﹣2)2=5
4.将一块长方形桌布铺在长为3m、宽为2m的长方形桌面上,各边下垂的长度相同,并且桌布的面积是桌面面积的2倍,那么桌布下垂的长度为( )
A.﹣2.5 B.2.5 C.0.5 D.﹣0.5
5.若a:b=3:4,且a+b=14,则2a﹣b的值是( )
A.4 B.2 C.20 D.14
6.如图,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③=; ④AC2=AD AB.其中能够单独判定△ABC∽△ACD的条件个数为( )
A.1 B.2 C.3 D.4
7.如图所示,在△ABC中,点D,E分别在AB,AC上,并且DE∥BC,,△ADE的面积为8,则△ABC的面积为( )
A.12 B.13 C.16 D.18
8.如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A. B. C. D.
9.如图,平面直角坐标系xOy中,点A、B的坐标分别为(4,0)、(2,﹣3),△AB′O′是△ABO关于点A的位似图形,且O'的坐标为(﹣2,0),则点B'的坐标为( )
A.(1,﹣5) B.(,﹣5) C.(1,) D.(,)
10.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来谷米1534石,验得其中夹有谷粒.现从中抽取谷米一把,共数得254粒,其中夹有谷粒28粒,则这批谷米内夹有谷粒约是( )
A.134石 B.169石 C.338石 D.1365石
11.如图所示,满足函数y=k(x﹣1)和y=(k≠0)的大致图象是( )
A.①② B.②③ C.②④ D.①④
12.如图,在平面直角坐标系中,Rt△ABC的顶点A、C的坐标分别为(0,2)、(2,0),∠ACB=90°,tan∠ABC=2,函数y=(k>0,x>0)的图象经过点B,则k的值为( )
A.2 B.2 C.3 D.4
二、填空题(本大题共6小题,每小题3分,共18分)
13.若点A(﹣3,y1),B(﹣2,y2),C(1,y3)都在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是 .
14.一个三角形的两边长分别为3和6,第三边长是方程x2﹣10x+21=0的根,则三角形的周长为 .
15.某市从2017年开始大力发展旅游产业.据统计该市2017年旅游收入约为2亿元,预计2019年旅游收入达到2.88亿元,据此估计该市2018年、2019年旅游收入的年平均增长率约为 .
16.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡脚α=45°,坡长AB=6米,背水坡CD的坡度i=1:,则背水CD的坡长为 米.
17.若△ABC∽△A′B′C′,且,△ABC的周长为12cm,则△A′B′C′的周长为 cm.
18.如图,点A1,A2,A3…在反比例函数y=(x>0)的图象上,点B1,B2,B3,…,Bn在y轴上,且∠B1OA1=∠B2B1A2=∠B3B2A3=…,直线y=x与双曲线y=交于点A1,B1A1⊥OA1,B2A2⊥B1A2,B3A3⊥B2A3,…,则B2022的坐标是 .
三、解答题(本大题共2小题,每小题6分,满分12分)
19.计算:2cos245°﹣﹣(sin60°﹣1)0+.
20.已知:平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+﹣=0的两个实数根.
(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么 ABCD的周长是多少?
四、解答题(本大题共2小题,每小题8分,满分16分)
21.争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分)
78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93
整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) 频数
78≤x<82 5
82≤x<86 a
86≤x<90 11
90≤x<94 b
94≤x<98 2
回答下列问题:
(1)以上30个数据中,中位数是 ;频数分布表中a= ;b= ;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.
22.如图,早上8:00,一艘轮船以15海里/小时的速度由南向北航行,在A处测得小岛P在北偏西15°方向上,到上午10:00,轮船在B处测得小岛P在北偏西30°方向上,在小岛P周围18海里内有暗礁,若轮船继续向前航行,有无触礁的危险?
五、解答题(本大题共2小题,每小题9分,满分18分)
23.某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,月底厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元;销售量在10部以上,每部返利1万元.
(1)若该公司当月售出3部汽车,则每部汽车的进价为 万元;
(2)如果汽车的售价为28万元/部,该公司计划当月盈利12万元,那么需要售出多少部汽车?(盈利=销售利润+返利)
24.如图,CD是Rt△ABC斜边上的高,E为CB的中点,ED的延长线交CA的延长线于点F.求证:AC CF=CB DF.
六、解答题(本大题共2小题,每小题10分,满分20分)
25.如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)若M(x1,y1)、N(x2,y2)是反比例函数y=上的两点,当x1<x2<0时,比较y2与y1的大小关系.
26.如图,矩形ABCD中,已知AB=6.BC=8,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F.将△ABE沿直线AE翻折,点B的对应点为点B'.
(1)如图1,若点E为线段BC上一点,延长AB'交CD于点M,求证:AM=FM;
(2)如图2,若点B'恰好落在对角线AC上,求的值;
(3)若=,求∠DAB'的正弦值.
参考答案
一、选择题(本大题共12小题,满分36分,每小题给出的四个选项中,只有一项是符合题目要求的,请把你认为符合题目要求的选项填涂在答题卡上相应题号下的方框里)
1.已知反比例函数y=﹣,这个函数的比例系数和自变量的取值范围是( )
A.k=﹣8;x≠0 B.k=﹣8;x>0 C.k=0;x>0 D.k=8;x≠0
【分析】反比例函数k的值就是比例系数,x在分母上,因此x≠0.
解:反比例函数k的值为:k=﹣8,自变量x的取值范围为x≠0,
故选:A.
2.将一元二次方程2x2+3x=1化成一般形式时,它的二次项、一次项系数和常数项分别为( )
A.2x2,﹣3,1 B.2x2,3,﹣1 C.﹣2x2,﹣3,﹣1 D.﹣2x2,3,1
【分析】根据一元二次方程的一般形式,ax2+bx+c=0(a,b,c是常数,a≠0)判断即可.
解:将一元二次方程2x2+3x=1化成一般形式为:2x2+3x﹣1=0,
∴它的二次项、一次项系数和常数项分别为:2x2,3,﹣1,
故选:B.
3.一元二次方程x2﹣4x﹣1=0配方后可化为( )
A.(x+2)2=3 B.(x+2)2=5 C.(x﹣2)2=3 D.( x﹣2)2=5
【分析】移项,配方,即可得出选项.
解:x2﹣4x﹣1=0,
x2﹣4x=1,
x2﹣4x+4=1+4,
(x﹣2)2=5,
故选:D.
4.将一块长方形桌布铺在长为3m、宽为2m的长方形桌面上,各边下垂的长度相同,并且桌布的面积是桌面面积的2倍,那么桌布下垂的长度为( )
A.﹣2.5 B.2.5 C.0.5 D.﹣0.5
【分析】设桌布铺到桌面上时各边垂下的长度为xm,则用含x的代数式表示桌布的长为(3+2x)m,宽为(2+2x)m,依题意得(2x+3)(2x+2)=2×3×2,列方程即可得到结论.
解:设桌布铺到桌面上时各边垂下的长度为xm,则桌布的长为(3+2x)m,宽为(2+2x)m,
依题意得(2x+3)(2x+2)=2×3×2,
解得x1=0.5,x2=﹣3(舍去),
答:桌布下垂的长度为0.5m,
故选:C.
5.若a:b=3:4,且a+b=14,则2a﹣b的值是( )
A.4 B.2 C.20 D.14
【分析】根据比例的性质得到3b=4a,结合a+b=14求得a、b的值,代入求值即可.
解:由a:b=3:4知3b=4a,
所以b=.
所以由a+b=14得到:a+=14,
解得a=6.
所以b=8.
所以2a﹣b=2×6﹣8=4.
故选:A.
6.如图,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③=; ④AC2=AD AB.其中能够单独判定△ABC∽△ACD的条件个数为( )
A.1 B.2 C.3 D.4
【分析】由图可知△ABC与△ACD中∠A为公共角,所以只要再找一组角相等,或一组对应边成比例即可解答.
解:有三个.
①∠B=∠ACD,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
②∠ADC=∠ACB,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定;
③中∠A不是已知的比例线段的夹角,不正确
④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定;
故选:C.
7.如图所示,在△ABC中,点D,E分别在AB,AC上,并且DE∥BC,,△ADE的面积为8,则△ABC的面积为( )
A.12 B.13 C.16 D.18
【分析】由DE∥BC可得△ADE∽△ABC,由可求得△ADE与△ABC的面积比为4:9,再由△ADE的面积为8,即可求出答案.
解:∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∵,
∴,
∵△ADE的面积为8,
∴,
∴△ABC的面积为18,
故选:D.
8.如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A. B. C. D.
【分析】取格点C,连接AC,BC,观察图象可知,O,B,C共线,∠ACO=90°,利用勾股定理求得AC和AO的长,根据正弦的定义即可求解.
解:取格点C,连接AC,BC,观察图象可知,O,B,C共线,∠ACO=90°,
∵AC=,AO===2,
∴sin∠AOB===.
故选:D.
9.如图,平面直角坐标系xOy中,点A、B的坐标分别为(4,0)、(2,﹣3),△AB′O′是△ABO关于点A的位似图形,且O'的坐标为(﹣2,0),则点B'的坐标为( )
A.(1,﹣5) B.(,﹣5) C.(1,) D.(,)
【分析】过点B作BE⊥x轴于点E,B′作B′F⊥x轴于点F,根据位似变换的性质得到==,根据相似三角形的性质列出比例式,计算即可.
解:过点B作BE⊥x轴于点E,B′作B′F⊥x轴于点F,
则BE∥B′F,
由题意得,OE=EA=2,BE=3,
∵点A、B的坐标分别为(4,0)、(2,﹣3),△AB′O′是△ABO关于的A的位似图形,且O′的坐标为(﹣2,0),
∴OB∥O′B′,
∴===,
∵BE∥B′F,
∴△AEB∽△AFB′,
∴===,即==,
解得,AF=3,B′F=,
∴OF=1,
则点B'的坐标为(1,﹣),
故选:C.
10.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来谷米1534石,验得其中夹有谷粒.现从中抽取谷米一把,共数得254粒,其中夹有谷粒28粒,则这批谷米内夹有谷粒约是( )
A.134石 B.169石 C.338石 D.1365石
【分析】根据254粒内夹谷28粒,可得比例,再乘以1534石,即可得出答案.
解:根据题意得:
1534×≈169(石),
答:这批谷米内夹有谷粒约169石;
故选:B.
11.如图所示,满足函数y=k(x﹣1)和y=(k≠0)的大致图象是( )
A.①② B.②③ C.②④ D.①④
【分析】分别根据一次函数与反比例函数图象的特点解答即可.
解:∵y=k(x﹣1),
∴函数y=k(x﹣1)过点(1,0),
故①④不合题意;
当k>0时,函数y=k(x﹣1)过第一、三、四象限,函数y=(k≠0)在一、三象限;
当k<0时,函数y=k(x﹣1)过第一、二、四象限,函数y=(k≠0)在二、四象限;
故②③符合题意;
故选:B.
12.如图,在平面直角坐标系中,Rt△ABC的顶点A、C的坐标分别为(0,2)、(2,0),∠ACB=90°,tan∠ABC=2,函数y=(k>0,x>0)的图象经过点B,则k的值为( )
A.2 B.2 C.3 D.4
【分析】过B点作BD⊥x轴于D,如图,先关键勾股定理得到AC=2,∠ACO=45°,再判断△BCD为等腰直角三角形得到CD=BD=BC,则可计算出CD=BD=1,所以B(3,1),然后利用反比例函数图象上点的坐标特征求出k的值.
解:过点B作BD⊥x轴,垂足为D,
∵点A、C的坐标分别为(0,2)、(2,0),
∴OA=OC=2,
在Rt△AOC中,AC===2,
又∵tan∠ABC=2,
∴tan∠ABC==2,
∴BC=AC=,
又∵∠ACB=90°,
∴∠OAC=∠OCA=45°=∠BCD=∠CBD,
∴CD=BD=BC=×=1,
∴OD=2+1=3,
∴B(3,1),
将点B的坐标代入y=得:k=3,
故选:C.
二、填空题(本大题共6小题,每小题3分,共18分)
13.若点A(﹣3,y1),B(﹣2,y2),C(1,y3)都在反比例函数y=﹣的图象上,则y1,y2,y3的大小关系是 y3<y1<y2 .
【分析】先根据函数解析式中的比例系数k确定函数图象所在的象限,再根据各象限内点的坐标特点及函数的增减性解答.
解:∵在反比例函数y=﹣中,k=﹣12<0,
∴此函数图象在第二、四象限,在每个象限内y随x增大而增大,
∵﹣3<﹣2<0,
∴点A(﹣3,y1),B(﹣2,y2)在第二象限,
∴0<y1<y2.
∵1>0,
∴C(1,y3)点在第四象限,
∴y3<0,
∴y3<y1<y2.
故答案为:y3<y1<y2.
14.一个三角形的两边长分别为3和6,第三边长是方程x2﹣10x+21=0的根,则三角形的周长为 16 .
【分析】首先求出方程的根,再根据三角形三边关系定理,确定第三边的长,进而求其周长.
解:解方程x2﹣10x+21=0得x1=3、x2=7,
∵3<第三边的边长<9,
∴第三边的边长为7.
∴这个三角形的周长是3+6+7=16.
故答案为:16.
15.某市从2017年开始大力发展旅游产业.据统计该市2017年旅游收入约为2亿元,预计2019年旅游收入达到2.88亿元,据此估计该市2018年、2019年旅游收入的年平均增长率约为 20% .
【分析】设该市2018年、2019年旅游收入的年平均增长率为x,根据该市2017年及2019年的旅游收入,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
解:设该市2018年、2019年旅游收入的年平均增长率为x,
依题意,得:2(1+x)2=2.88,
解得:x1=0.2=20%,x2=﹣2.2(不合题意,舍去).
故答案为:20%.
16.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡脚α=45°,坡长AB=6米,背水坡CD的坡度i=1:,则背水CD的坡长为 12 米.
【分析】根据正弦的定义求出AE,进而求出DF,根据坡度的概念求出FC,根据勾股定理计算,得到答案.
解:由题意可知,四边形AEFD为矩形,
∴DF=AE,
在Rt△ABE中,∠B=45°,AB=6米,
则AE=AB sinB=6×=6(米),
∴DF=6米,
∵背水坡CD的坡度i=1:,
∴FC=6米,
∴CD===12(米),
故答案为:12.
17.若△ABC∽△A′B′C′,且,△ABC的周长为12cm,则△A′B′C′的周长为 16 cm.
【分析】根据相似三角形周长的比等于相似比求解.
解:∵△ABC∽△A′B′C′,且,即相似三角形的相似比是
∵△ABC的周长为12cm
∴△A′B′C′的周长为12÷=16cm.
18.如图,点A1,A2,A3…在反比例函数y=(x>0)的图象上,点B1,B2,B3,…,Bn在y轴上,且∠B1OA1=∠B2B1A2=∠B3B2A3=…,直线y=x与双曲线y=交于点A1,B1A1⊥OA1,B2A2⊥B1A2,B3A3⊥B2A3,…,则B2022的坐标是 (0,2) .
【分析】由题意,△OA1B1,△B1A2B2,△B2A3B3,…,都是等腰直角三角形,想办法求出OB1,OB2,OB3,OB4,…,探究规律,利用规律解决问题即可得出结论.
解:由题意,△OA1B1,△B1A2B2,△B2A3B3,…,都是等腰直角三角形,
∵A1(1,1),
∴OB1=2,设A2(m,2+m),
则有m(2+m)=1,
解得m=﹣1,
∴OB2=2,
设A3(a,2+a),则有a(2+a)=1,
解得a=﹣,
∴OB3=2,
同法可得,OB4=2,
∴OBn=2,
∴Bn(0,2),
∴B2022(0,2),
故答案为:.
三、解答题(本大题共2小题,每小题6分,满分12分)
19.计算:2cos245°﹣﹣(sin60°﹣1)0+.
【分析】将特殊角的三角函数值代入,然后进行负整数指数幂的运算,将各部分化为最简后合并即可得出答案.
解:原式=2×()2﹣|2﹣|﹣1+4
=1﹣(2﹣)﹣1+4
=+2.
20.已知:平行四边形ABCD的两边AB,AD的长是关于x的方程x2﹣mx+﹣=0的两个实数根.
(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么 ABCD的周长是多少?
【分析】(1)根据菱形的性质可得出AB=AD,结合根的判别式,即可得出关于m的一元二次方程,解之即可得出m的值,将其代入原方程,解之即可得出菱形的边长;
(2)将x=2代入原方程可求出m的值,将m的值代入原方程结合根与系数的关系可求出方程的另一根AD的长,再根据平行四边形的周长公式即可求出 ABCD的周长.
解:(1)∵四边形ABCD是菱形,
∴AB=AD.
又∵AB、AD的长是关于x的方程x2﹣mx+﹣=0的两个实数根,
∴Δ=(﹣m)2﹣4×(﹣)=(m﹣1)2=0,
∴m=1,
∴当m为1时,四边形ABCD是菱形.
当m=1时,原方程为x2﹣x+=0,即(x﹣)2=0,
解得:x1=x2=,
∴菱形ABCD的边长是.
(2)把x=2代入原方程,得:4﹣2m+﹣=0,
解得:m=.
将m=代入原方程,得:x2﹣x+1=0,
∴方程的另一根AD=1÷2=,
∴ ABCD的周长是2×(2+)=5.
四、解答题(本大题共2小题,每小题8分,满分16分)
21.争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分)
78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93
整理上面的数据得到频数分布表和频数分布直方图:
成绩(分) 频数
78≤x<82 5
82≤x<86 a
86≤x<90 11
90≤x<94 b
94≤x<98 2
回答下列问题:
(1)以上30个数据中,中位数是 86 ;频数分布表中a= 6 ;b= 6 ;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.
【分析】(1)将各数按照从小到大顺序排列,找出中位数,根据统计图与表格确定出a与b的值即可;
(2)补全直方图即可;
(3)求出样本中游戏学生的百分比,乘以300即可得到结果.
解:(1)根据题意排列得:78,81,81,81,81,83,83,84,84,85,85,86,86,86,86,86,86,88,89,89,89,89,90,92,92,93,93,93,94,97,可得中位数为86,频数分布表中a=6,b=6;
故答案为:86;6;6;
(2)补全频数分布直方图,如图所示:
(3)根据题意得:300×=190(人),
则该校七年级300名学生中,达到优秀等级的人数估计为190人.
22.如图,早上8:00,一艘轮船以15海里/小时的速度由南向北航行,在A处测得小岛P在北偏西15°方向上,到上午10:00,轮船在B处测得小岛P在北偏西30°方向上,在小岛P周围18海里内有暗礁,若轮船继续向前航行,有无触礁的危险?
【分析】过点P作PD⊥AC于点D,利用三角形外角可求出∠P,利用角的度数可判断△PAB为等腰三角形,利用时间和速度可求出AB的长度,也就求出PB的长,再利用PD=即可求得PD的长度,与18比较即可得出结论.
解:如图,过点P作PD⊥AC于点D,
∵∠PAB=15°,∠PBD=30°,
∴∠APB=15°,
∴∠PAB=∠APB,
∴PB=AB,
∵AB=15×2=30(海里),
∴PB==30(海里),
在Rt△PBD中,∠PDB=90°,∠PBD=30°,
∴PD==30=15<18,
∴轮船继续向前航行,有触礁的危险.
五、解答题(本大题共2小题,每小题9分,满分18分)
23.某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,月底厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元;销售量在10部以上,每部返利1万元.
(1)若该公司当月售出3部汽车,则每部汽车的进价为 26.8 万元;
(2)如果汽车的售价为28万元/部,该公司计划当月盈利12万元,那么需要售出多少部汽车?(盈利=销售利润+返利)
【分析】(1)根据若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,得出该公司当月售出3部汽车时,则每部汽车的进价为:27﹣0.1×2,即可得出答案;
(2)利用设需要售出x部汽车,由题意可知,每部汽车的销售利润,根据当0≤x≤10,以及当x>10时,分别讨论得出即可.
解:(1)∵若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,
∴若该公司当月售出3部汽车,则每部汽车的进价为:27﹣0.1×(3﹣1)=26.8,
故答案为:26.8;
(2)设需要售出x部汽车,
由题意可知,每部汽车的销售利润为:
28﹣[27﹣0.1(x﹣1)]=(0.1x+0.9)(万元),
当0≤x≤10,
根据题意,得x (0.1x+0.9)+0.5x=12,
整理,得x2+14x﹣120=0,
解这个方程,得x1=﹣20(不合题意,舍去),x2=6,
当x>10时,
根据题意,得x (0.1x+0.9)+x=12,
整理,得x2+19x﹣120=0,
解这个方程,得x1=﹣24(不合题意,舍去),x2=5,
因为5<10,所以x2=5舍去.
答:需要售出6部汽车.
24.如图,CD是Rt△ABC斜边上的高,E为CB的中点,ED的延长线交CA的延长线于点F.求证:AC CF=CB DF.
【分析】先证明△FDA∽△FCD,得出,再证明△ACD∽△CBD,可得,即可解答.
【解答】证明:∵CD⊥AB,
∴∠ADC=∠CDB=90°,
∵E为CB的中点,
∴CE=EB=DE=BC,
∴∠B=∠BDE,
∵∠BDE=∠ADF,
∴∠B=∠ADF,
∵∠ACB=90°,
∴∠B+∠CAB=90°,
∵∠ACD+∠CAB=90°
∴∠B=∠ACD,
∴∠ADF=∠ACD,
又∵∠F=∠F,
∴△FDA∽△FCD,
∴,
∵∠ADC=∠CDB=90°,∠ACD=∠B,
∴△ACD∽△CBD,
∴,
∴,
即AC CF=CB DF.
六、解答题(本大题共2小题,每小题10分,满分20分)
25.如图,一次函数y=kx+b的图象与反比例函数y=的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C.
(1)求一次函数与反比例函数的解析式;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)若M(x1,y1)、N(x2,y2)是反比例函数y=上的两点,当x1<x2<0时,比较y2与y1的大小关系.
【分析】(1)利用待定系数法即可解决求问题.
(2)根据对称性求出点D坐标,发现BD∥x轴,利用三角形的面积公式计算即可.
(3)利用反比例函数的增减性解决问题即可.
解:(1)∵反比例函数y=经过点B(2,﹣1),
∴m=﹣2,
∵点A(﹣1,n)在y=上,
∴n=2,
∴A(﹣1,2),
把A,B坐标代入y=kx+b,则有,
解得,
∴一次函数的解析式为y=﹣x+1,反比例函数的解析式为y=﹣.
(2)∵直线y=﹣x+1交y轴于C,
∴C(0,1),
∵D,C关于x轴对称,
∴D(0,﹣1),∵B(2,﹣1)
∴BD∥x轴,
∴S△ABD=×2×3=3.
(3)∵M(x1,y1)、N(x2,y2)是反比例函数y=﹣上的两点,且x1<x2<0,
∴y1<y2.
26.如图,矩形ABCD中,已知AB=6.BC=8,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F.将△ABE沿直线AE翻折,点B的对应点为点B'.
(1)如图1,若点E为线段BC上一点,延长AB'交CD于点M,求证:AM=FM;
(2)如图2,若点B'恰好落在对角线AC上,求的值;
(3)若=,求∠DAB'的正弦值.
【分析】(1)由折叠的性质及等腰三角形的判定可得出答案;
(2)由勾股定理求出AC=10,证明△ABE∽△FCE,由比例线段可得出答案;
(3)①点E在线段BC上,设DM=x,根据Rt△ADM中,AM2=AD2+DM2,得到关于x的方程,求得x的值,最后根据sin∠DAB'=进行计算即可;②当点E在线段BC的延长线上时,设DM=x,得出(2+x)2=82+x2,求出x=15.则AM=17,可得出答案.
【解答】(1)证明:∵四边形ABCD为矩形,
∴AB∥CD,
∴∠F=∠BAF,
由折叠可知:∠BAF=∠MAF,
∴∠F=∠MAF,
∴AM=FM.
(2)解:同(1)的证法可得△ACF是等腰三角形,AC=CF,
在Rt△ABC中,∵AB=6,BC=8,
∴AC===10,
∴CF=AC=10,
∵AB∥CF,
∴△ABE∽△FCE,
∴;
(3)①当点E在线段BC上时,如图3,AB'的延长线交CD于点M,
由AB∥CF可得:△ABE∽△FCE,
∴,即,
∴CF=4,
同(1)的证法可得AM=FM.
设DM=x,则MC=6﹣x,则AM=FM=10﹣x,
在Rt△ADM中,AM2=AD2+DM2,即(10﹣x)2=82+x2,
解得:x=,
则AM=10﹣x=10﹣=,
∴sin∠DAB'==.
②当点E在线段BC的延长线上时,如图4,
由AB∥CF可得:△ABE∽△FCE,
∴,即,
∴CF=4,
则DF=6﹣4=2,
设DM=x,同理可得出AM=FM=2+x,
∵AM2=AD2+DM2,
∴(2+x)2=82+x2,
解得x=15.
∴AM=17,
∴sin∠DAB'=.
综合以上可得,∠DAB'的正弦值为或.
同课章节目录
