2021-2022学年江苏省盐城市东台市教育联合体八年级(下)开学数学试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年江苏省盐城市东台市教育联合体八年级(下)开学数学试卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 569.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 10:45:43 | ||
图片预览



文档简介
2021-2022学年江苏省盐城市东台市教育联合体八年级(下)开学数学试卷
一、选择题。(本大题共有8小题,每小题3分,共24分)
1.下列四个数学符号中,是轴对称图形的是( )
A.≌ B.⊥ C.≠ D.≥
2.平面直角坐标系中,在第二象限的点是( )
A.(1,1) B.(1,﹣1) C.(﹣1,1) D.(﹣1,﹣1)
3.一次函数y=﹣2x+5的图象不经过的象限是( )
A.一 B.二 C.三 D.四
4.下列四组数据中,不能作为直角三角形三边长的是( )
A.1,,2 B.5,12,13 C.5,6,7 D.7,24,25
5.在△ABC中和△DEF中,已知BC=EF,∠C=∠F,增加下列条件后还不能判定△ABC≌△DEF的是( )
A.AC=DF B.AB=DE C.∠A=∠D D.∠B=∠E
6.∠AOB的平分线上一点P到OA的距离为4,Q是OB上任一点,则( )
A.PQ≥4 B.PQ>4 C.PQ≤4 D.PQ<4
7.已知实数x,y满足+(y+1)2=0,则x﹣y等于( )
A.1 B.﹣1 C.﹣3 D.3
8.如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确有( )
①△BPQ是等边三角形;②△PCQ是直角三角形;③∠APB=150°;④∠APC=120°.
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题。(本大题共有8小题,每小题3分,共24分)
9.将直线y=﹣2x向上平移1个单位长度,平移后直线的解析式为 .
10.已知,等腰三角形的两边长分别为5cm和11cm,则它的周长是 cm.
11.在平面直角坐标系中,点(﹣3,5)关于x轴对称的点的坐标为 .
12.已知y关于x的函数y=﹣x+2+m是正比例函数,则m= .
13.截止北京时间2021年12月20日全球累计确诊新冠肺炎病例约为274950000例,将这个数精确到十万位为 例.
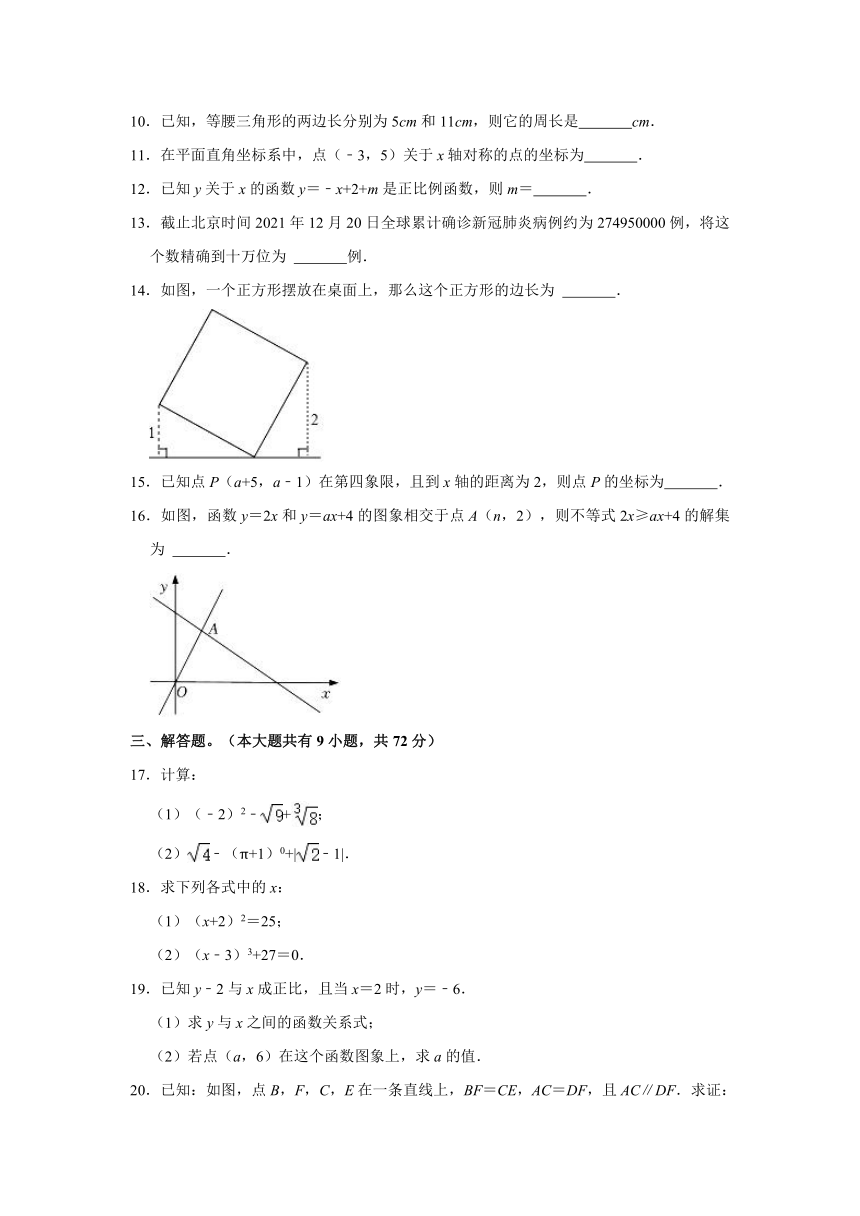
14.如图,一个正方形摆放在桌面上,那么这个正方形的边长为 .
15.已知点P(a+5,a﹣1)在第四象限,且到x轴的距离为2,则点P的坐标为 .
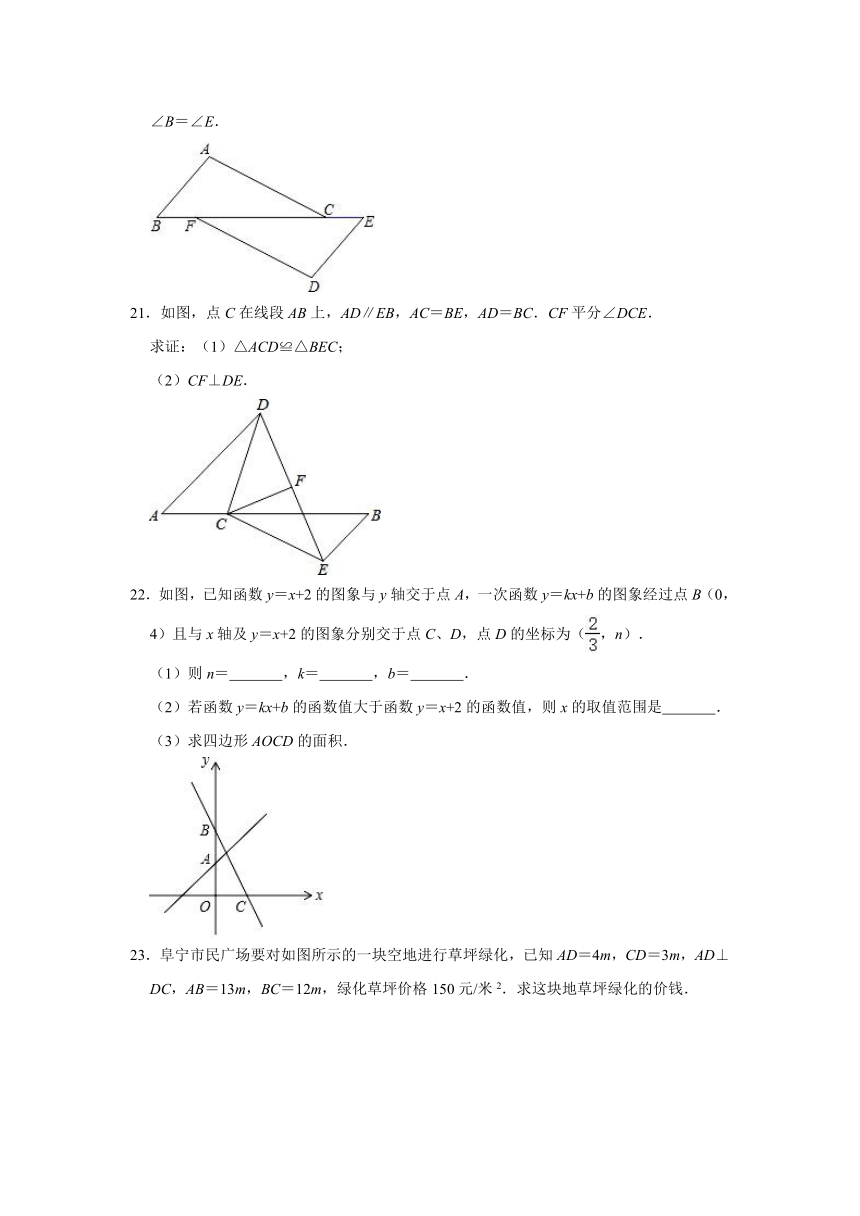
16.如图,函数y=2x和y=ax+4的图象相交于点A(n,2),则不等式2x≥ax+4的解集为 .
三、解答题。(本大题共有9小题,共72分)
17.计算:
(1)(﹣2)2﹣+;
(2)﹣(π+1)0+|﹣1|.
18.求下列各式中的x:
(1)(x+2)2=25;
(2)(x﹣3)3+27=0.
19.已知y﹣2与x成正比,且当x=2时,y=﹣6.
(1)求y与x之间的函数关系式;
(2)若点(a,6)在这个函数图象上,求a的值.
20.已知:如图,点B,F,C,E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:∠B=∠E.
21.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
22.如图,已知函数y=x+2的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,4)且与x轴及y=x+2的图象分别交于点C、D,点D的坐标为(,n).
(1)则n= ,k= ,b= .
(2)若函数y=kx+b的函数值大于函数y=x+2的函数值,则x的取值范围是 .
(3)求四边形AOCD的面积.
23.阜宁市民广场要对如图所示的一块空地进行草坪绿化,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m,绿化草坪价格150元/米2.求这块地草坪绿化的价钱.
24.如图,将长方形ABCD沿EF折叠,使点D与点B重合.
(1)若∠AEB=40°,求∠BFE的度数;
(2)若AB=6,AD=18,求CF的长.
25.如图,一次函数y=ax+b与正比例函数y=kx的图象交于点M.
(1)求正比例函数和一次函数的解析式;
(2)根据图象,写出关于x的不等式kx>ax+b的解集;
(3)求△MOP的面积.
参考答案
一、选择题。(本大题共有8小题,每小题3分,共24分)
1.下列四个数学符号中,是轴对称图形的是( )
A.≌ B.⊥ C.≠ D.≥
【分析】利用轴对称图形定义进行解答即可.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:选项A、C、D均不能找到这样的一条直线,使这个图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
选项B能找到这样的一条直线,使这个图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
2.平面直角坐标系中,在第二象限的点是( )
A.(1,1) B.(1,﹣1) C.(﹣1,1) D.(﹣1,﹣1)
【分析】根据各象限内点的坐标特征对各选项分析判断后利用排除法求解.
解:A、(1,1)在第一象限,故本选项错误;
B、(1,﹣1)在第四象限,故本选项错误;
C、(﹣1,1)在第二象限,故本选项正确;
D、(﹣1,﹣1)在第三象限,故本选项错误.
故选:C.
3.一次函数y=﹣2x+5的图象不经过的象限是( )
A.一 B.二 C.三 D.四
【分析】根据一次函数的解析式和一次函数的性质,可以得到该函数的图象经过哪几个象限,不经过哪个象限.
解:∵一次函数y=﹣2x+5,k=﹣2<0,b=5>0,
∴该函数图象经过第一、二、四象限,不经过第三象限,
故选:C.
4.下列四组数据中,不能作为直角三角形三边长的是( )
A.1,,2 B.5,12,13 C.5,6,7 D.7,24,25
【分析】利用勾股定理逆定理进行判断即可.
解:A、12+()2=22,能构成直角三角形,故此选项不合题意;
B、52+122=132,能构成直角三角形,故此选项不符合题意;
C、52+62≠72,不能构成直角三角形,故此选项符合题意;
D、72+242=252,能构成直角三角形,故此选项不合题意.
故选:C.
5.在△ABC中和△DEF中,已知BC=EF,∠C=∠F,增加下列条件后还不能判定△ABC≌△DEF的是( )
A.AC=DF B.AB=DE C.∠A=∠D D.∠B=∠E
【分析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理进行判断即可.
解:
A、根据SAS即可推出△ABC≌△DEF,故本选项错误;
B、不能推出△ABC≌△DEF,故本选项正确;
C、根据AAS即可推出△ABC≌△DEF,故本选项错误;
D、根据ASA即可推出△ABC≌△DEF,故本选项错误;
故选:B.
6.∠AOB的平分线上一点P到OA的距离为4,Q是OB上任一点,则( )
A.PQ≥4 B.PQ>4 C.PQ≤4 D.PQ<4
【分析】过点P作PE⊥OB于E,根据角平分线上的点到角的两边距离相等可得PD=PE,再根据垂线段最短解答.
解:如图,过点P作PE⊥OB于E,
∵OP是∠AOB的平分线,
∴PD=PE=10,
∵Q是OB上任一点,
∴PQ≥PE,
∴PQ≥4.
故选:A.
7.已知实数x,y满足+(y+1)2=0,则x﹣y等于( )
A.1 B.﹣1 C.﹣3 D.3
【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.
解:∵+(y+1)2=0,而,(y+1)2≥0,
∴x﹣2=0,y+1=0,
解得x=2,y=﹣1,
∴x﹣y=2﹣(﹣1)=2+1=3.
故选:D.
8.如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确有( )
①△BPQ是等边三角形;②△PCQ是直角三角形;③∠APB=150°;④∠APC=120°.
A.①②③ B.①②④ C.②③④ D.①②③④
【分析】①根据△ABC是等边三角形,得出∠ABC=60°,根据△BQC≌△BPA,得出∠CBQ=∠ABP,PB=QB=4,PA=QC=3,∠BPA=∠BQC,求出∠PBQ=60°,即可判断①;
②根据勾股定理的逆定理即可判断得出②;
③根据△BPQ是等边三角形,△PCQ是直角三角形即可判断;
④求出∠APC=150°﹣∠QPC,和PC≠2QC,可得∠QPC≠30°,即可判断④.
解:①∵△ABC是等边三角形,
∴∠ABC=60°,
∵△BQC≌△BPA,
∴∠CBQ=∠ABP,PB=QB=4,
PA=QC=3,∠BPA=∠BQC,
∴∠PBQ=∠PBC+∠CBQ=∠PBC+∠ABP=∠ABC=60°,
∴△BPQ是等边三角形,
所以①正确;
②PQ=PB=4,
PQ2+QC2=42+32=25,
PC2=52=25,
∴PQ2+QC2=PC2,
∴∠PQC=90°,
∴△PCQ是直角三角形,
所以②正确;
③∵△BPQ是等边三角形,
∴∠PQB=∠BPQ=60°,
∴∠APB=∠BQC=∠BQP+∠PQC=60°+90°=150°,
所以③正确;
④∠APC=360°﹣150°﹣60°﹣∠QPC=150°﹣∠QPC,
∵∠PQC=90°,PC≠2QC,
∴∠QPC≠30°,
∴∠APC≠120°.
所以④错误.
所以正确的有①②③,
故选:A.
二、填空题。(本大题共有8小题,每小题3分,共24分)
9.将直线y=﹣2x向上平移1个单位长度,平移后直线的解析式为 y=﹣2x+1 .
【分析】根据一次函数图象上下平移时解析式的变化规律求解.
解:将直线y=﹣2x向上平移1个单位,得到的直线的解析式为y=﹣2x+1.
故答案为y=﹣2x+1.
10.已知,等腰三角形的两边长分别为5cm和11cm,则它的周长是 27 cm.
【分析】因为边为5cm和11cm,没说是底边还是腰,所以有两种情况,需要分类讨论.
解:当5cm为底时,
其它两边都为11cm,
5cm、11cm、11cm可以构成三角形,
周长为27cm;
当5cm为腰时,
其它两边为5cm和11cm,
∵5+5=10<11,所以不能构成三角形,故舍去,
∴答案只有27cm.
故填27.
11.在平面直角坐标系中,点(﹣3,5)关于x轴对称的点的坐标为 (﹣3,﹣5) .
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得答案.
解:在平面直角坐标系中,点(﹣3,5)关于x轴对称的点的坐标为(﹣3,﹣5),
故答案为:(﹣3,﹣5).
12.已知y关于x的函数y=﹣x+2+m是正比例函数,则m= ﹣2 .
【分析】根据正比例函数的定义得到2+m=0,然后解方程可得m的值.
解:∵y关于x的函数y=﹣x+2+m是正比例函数,
∴2+m=0,
解得m=﹣2.
故答案为:﹣2.
13.截止北京时间2021年12月20日全球累计确诊新冠肺炎病例约为274950000例,将这个数精确到十万位为 2.750×108 例.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,且比原数的整数位少一位;取精确度时,需要精确到哪位就数到哪位,然后根据四舍五入的原理进行取舍.
解:274950000≈2.750×108,
故选:2.750×108.
14.如图,一个正方形摆放在桌面上,那么这个正方形的边长为 .
【分析】标注字母,根据正方形的性质可得AB=AD,∠BAD=90°,再根据同角的余角相等求出∠1=∠3,然后利用“角角边”字母△ABE和△DAF全等,根据全等三角形对应边相等可得AE=DF,再利用勾股定理列式计算即可得解.
解:如图,由正方形性质可得,AB=AD,∠BAD=90°,
∴∠1+∠2=180°﹣90°=90°,
∵BE⊥AE,DF⊥AF,
∴∠AEB=90°,∠DFA=90°,
∴∠2+∠3=180°﹣90°=90°,
∴∠1=∠3,
在△ABE和△DAF中,
,
∴△ABE≌△DAF(AAS),
∴AE=DF=1,
在Rt△ABE中,AB===,
即正方形的边长为,
故答案为:.
15.已知点P(a+5,a﹣1)在第四象限,且到x轴的距离为2,则点P的坐标为 (4,﹣2) .
【分析】根据第四象限内点的坐标特征得到a+5>0,a﹣1<0,然后解不等式组即可.
解:∵点P(a+5,a﹣1)在第四象限,且到x轴的距离为2,
∴a+5>0,a﹣1<0,a﹣1=±2,
∴a=﹣1.
点P的坐标为(4,﹣2),
故答案为(4,﹣2)
16.如图,函数y=2x和y=ax+4的图象相交于点A(n,2),则不等式2x≥ax+4的解集为 x≥1 .
【分析】观察图象,写出直线y=2x没在直线y=ax+4的下方所对应的自变量的范围即可.
解:∵函数y=2x的图象经过点A(n,2),
∴2n=2,
解得:n=1,
∴点A(1,2),
当x≥1时,2x≥ax+4,
即不等式2x≥ax+4的解集为x≥1.
故答案为:x≥1.
三、解答题。(本大题共有9小题,共72分)
17.计算:
(1)(﹣2)2﹣+;
(2)﹣(π+1)0+|﹣1|.
【分析】(1)首先计算乘方、开方和开立方,然后从左向右依次计算,求出算式的值即可.
(2)首先计算零指数幂、开方和绝对值,然后从左向右依次计算,求出算式的值即可.
解:(1)(﹣2)2﹣+
=4﹣3+2
=3.
(2)﹣(π+1)0+|﹣1|
=2﹣1+(﹣1)
=1+﹣1
=.
18.求下列各式中的x:
(1)(x+2)2=25;
(2)(x﹣3)3+27=0.
【分析】(1)先直接开平方得x+2=±5,解出x;
(2)先直接开立方得x﹣3=﹣3,解出x;
解:(1)(x+2)2=25,
x+2=±5,
x1=﹣7,x2=3;
(2)(x﹣3)3+27=0,
x﹣3=﹣3,
x=0.
19.已知y﹣2与x成正比,且当x=2时,y=﹣6.
(1)求y与x之间的函数关系式;
(2)若点(a,6)在这个函数图象上,求a的值.
【分析】(1)根据题意设y﹣2=kx(k≠0),把x=2,y=﹣6代入求出k的值,即可确定出y与x的函数关系式;
(2)把(a,6)代入函数解析式求出a的值即可.
解:(1)设y﹣2=kx(k≠0),
把x=2,y=﹣6代入得:﹣6﹣2=2k,
解得:k=﹣4,
则该函数关系式为:y=﹣4x+2;
(2)∵点(a,6)在函数y=﹣4x+2图象上,
∴6=﹣4a+2,
∴a=﹣1.
20.已知:如图,点B,F,C,E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:∠B=∠E.
【分析】先证出BC=EF,∠ACB=∠DFE,再证明△ACB≌△DFE,得出对应角相等即可.
【解答】证明:∵BF=CE,
∴BC=EF,
∵AC∥DF,
∴∠ACB=∠DFE,
在△ACB和△DFE中,
,
∴△ACB≌△DFE(SAS),
∴∠B=∠E.
21.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
【分析】(1)根据平行线性质求出∠A=∠B,根据SAS推出即可.
(2)根据全等三角形性质推出CD=CE,根据等腰三角形性质求出即可.
【解答】证明:(1)∵AD∥BE,
∴∠A=∠B,
在△ACD和△BEC中
∴△ACD≌△BEC(SAS),
(2)∵△ACD≌△BEC,
∴CD=CE,
又∵CF平分∠DCE,
∴CF⊥DE.
22.如图,已知函数y=x+2的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,4)且与x轴及y=x+2的图象分别交于点C、D,点D的坐标为(,n).
(1)则n= ,k= ﹣2 ,b= 4 .
(2)若函数y=kx+b的函数值大于函数y=x+2的函数值,则x的取值范围是 x< .
(3)求四边形AOCD的面积.
【分析】(1)根据点D在函数y=x+2的图象上,即可求出n的值;再利用待定系数法求出k,b的值;
(2)根据图象,直接判断即可;
(3)用三角形OBC的面积减去三角形ABD的面积即可.
解:(1)∵点D(,n)在直线y=x+2上,
∴n=+2=,
∵一次函数经过点B(0,4)、点D(,),
∴,解得:,
故答案为:,﹣2,4;
(2)由图象可知,函数y=kx+b大于函数y=x+2时,图象在直线x=的左侧,
∴x<,
故答案为:x<,
(3)直线y=﹣2x+4与x轴交于点C,
∴令y=0,得:﹣2x+4=0,解得x=2,
∴点C的坐标为(2,0),
∵函数y=x+2的图象与y轴交于点A,
∴令x=0,得:y=2,
∴点A的坐标为(0,2),
S△BOC=×2×4=4,
S△BAD=×(4﹣2)×=,
∴S四边形AOCD=S△BOC﹣S△BAD=4﹣=.
23.阜宁市民广场要对如图所示的一块空地进行草坪绿化,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m,绿化草坪价格150元/米2.求这块地草坪绿化的价钱.
【分析】根据勾股定理求得AC的长,再根据勾股定理的逆定理判定△ABC为直角三角形,从而不难求得这块地的面积.
解:连接AC,
∵AD⊥DC,
∴∠ADC=90°,
在Rt△ADC中,根据勾股定理,得,
AC==5,
在△ABC中,∵AC2+BC2=52+122=132=AB2,
∴△ABC是直角三角形,
∴S四边形ABCD=S△ABC﹣S△ACD
=
=24(m2),
∴这块地草坪绿化的价钱=24×150=3600(元).
24.如图,将长方形ABCD沿EF折叠,使点D与点B重合.
(1)若∠AEB=40°,求∠BFE的度数;
(2)若AB=6,AD=18,求CF的长.
【分析】(1)根据平角的定义和折叠的性质即可得到结论;
(2)首先设CF=x,则FG=CF=x,BF=BC﹣CF=18﹣x,然后在直角△BGF利用勾股定理求出x即可.
解:(1)∵∠AEB=40°,
∴∠BED=180°﹣∠AEB=140°,
∵将长方形ABCD沿EF折叠,使点D与点B重合,
∴∠BEF=∠DEF=BED=70°,
∵AD∥BC,
∴∠BFE=∠DEF=70°;
(2)设CF=x,则FG=CF=x,BF=BC﹣CF=18﹣x,
∵将长方形ABCD沿EF折叠,使点D与点B重合,
∴∠G=∠C=90°,BG=CD=AB=6,
在Rt△BGF中,BG2+GF2=BF2,
则62+x2=(18﹣x)2,
解得:x=8.
∴CF=8.
25.如图,一次函数y=ax+b与正比例函数y=kx的图象交于点M.
(1)求正比例函数和一次函数的解析式;
(2)根据图象,写出关于x的不等式kx>ax+b的解集;
(3)求△MOP的面积.
【分析】(1)先利用待定系数法求出一次函数解析式,再利用一次函数解析式确定M点的坐标,然后根据待定系数法求出正比例函数解析式;
(2)结合图象写出正比例函数图象在直线y=ax+b的上方所对应的自变量的范围即可;
(3)先利用一次函数解析式求出P点坐标,然后利用三角形面积公式.
解:(1)∵y=ax+b经过(1,0)和(0,﹣2),
∴,解得k=2,b=﹣2,
∴一次函数表达式为:y=2x﹣2
∵点M在该一次函数图象上,
∴m=2×2﹣2=2,则M点坐标为(2,2);
又∵M在函数y=kx图象上,
∴2k=2,解得k=1,
∴正比例函数的解析式为y=x;
(2)由图象可知,x<2时,x>2x﹣2
(3)当y=0时,2x﹣2=0,解得x=1,则P(1,0),
∴S△MOP=×1×2=1.
一、选择题。(本大题共有8小题,每小题3分,共24分)
1.下列四个数学符号中,是轴对称图形的是( )
A.≌ B.⊥ C.≠ D.≥
2.平面直角坐标系中,在第二象限的点是( )
A.(1,1) B.(1,﹣1) C.(﹣1,1) D.(﹣1,﹣1)
3.一次函数y=﹣2x+5的图象不经过的象限是( )
A.一 B.二 C.三 D.四
4.下列四组数据中,不能作为直角三角形三边长的是( )
A.1,,2 B.5,12,13 C.5,6,7 D.7,24,25
5.在△ABC中和△DEF中,已知BC=EF,∠C=∠F,增加下列条件后还不能判定△ABC≌△DEF的是( )
A.AC=DF B.AB=DE C.∠A=∠D D.∠B=∠E
6.∠AOB的平分线上一点P到OA的距离为4,Q是OB上任一点,则( )
A.PQ≥4 B.PQ>4 C.PQ≤4 D.PQ<4
7.已知实数x,y满足+(y+1)2=0,则x﹣y等于( )
A.1 B.﹣1 C.﹣3 D.3
8.如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确有( )
①△BPQ是等边三角形;②△PCQ是直角三角形;③∠APB=150°;④∠APC=120°.
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题。(本大题共有8小题,每小题3分,共24分)
9.将直线y=﹣2x向上平移1个单位长度,平移后直线的解析式为 .
10.已知,等腰三角形的两边长分别为5cm和11cm,则它的周长是 cm.
11.在平面直角坐标系中,点(﹣3,5)关于x轴对称的点的坐标为 .
12.已知y关于x的函数y=﹣x+2+m是正比例函数,则m= .
13.截止北京时间2021年12月20日全球累计确诊新冠肺炎病例约为274950000例,将这个数精确到十万位为 例.
14.如图,一个正方形摆放在桌面上,那么这个正方形的边长为 .
15.已知点P(a+5,a﹣1)在第四象限,且到x轴的距离为2,则点P的坐标为 .
16.如图,函数y=2x和y=ax+4的图象相交于点A(n,2),则不等式2x≥ax+4的解集为 .
三、解答题。(本大题共有9小题,共72分)
17.计算:
(1)(﹣2)2﹣+;
(2)﹣(π+1)0+|﹣1|.
18.求下列各式中的x:
(1)(x+2)2=25;
(2)(x﹣3)3+27=0.
19.已知y﹣2与x成正比,且当x=2时,y=﹣6.
(1)求y与x之间的函数关系式;
(2)若点(a,6)在这个函数图象上,求a的值.
20.已知:如图,点B,F,C,E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:∠B=∠E.
21.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
22.如图,已知函数y=x+2的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,4)且与x轴及y=x+2的图象分别交于点C、D,点D的坐标为(,n).
(1)则n= ,k= ,b= .
(2)若函数y=kx+b的函数值大于函数y=x+2的函数值,则x的取值范围是 .
(3)求四边形AOCD的面积.
23.阜宁市民广场要对如图所示的一块空地进行草坪绿化,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m,绿化草坪价格150元/米2.求这块地草坪绿化的价钱.
24.如图,将长方形ABCD沿EF折叠,使点D与点B重合.
(1)若∠AEB=40°,求∠BFE的度数;
(2)若AB=6,AD=18,求CF的长.
25.如图,一次函数y=ax+b与正比例函数y=kx的图象交于点M.
(1)求正比例函数和一次函数的解析式;
(2)根据图象,写出关于x的不等式kx>ax+b的解集;
(3)求△MOP的面积.
参考答案
一、选择题。(本大题共有8小题,每小题3分,共24分)
1.下列四个数学符号中,是轴对称图形的是( )
A.≌ B.⊥ C.≠ D.≥
【分析】利用轴对称图形定义进行解答即可.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
解:选项A、C、D均不能找到这样的一条直线,使这个图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
选项B能找到这样的一条直线,使这个图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
2.平面直角坐标系中,在第二象限的点是( )
A.(1,1) B.(1,﹣1) C.(﹣1,1) D.(﹣1,﹣1)
【分析】根据各象限内点的坐标特征对各选项分析判断后利用排除法求解.
解:A、(1,1)在第一象限,故本选项错误;
B、(1,﹣1)在第四象限,故本选项错误;
C、(﹣1,1)在第二象限,故本选项正确;
D、(﹣1,﹣1)在第三象限,故本选项错误.
故选:C.
3.一次函数y=﹣2x+5的图象不经过的象限是( )
A.一 B.二 C.三 D.四
【分析】根据一次函数的解析式和一次函数的性质,可以得到该函数的图象经过哪几个象限,不经过哪个象限.
解:∵一次函数y=﹣2x+5,k=﹣2<0,b=5>0,
∴该函数图象经过第一、二、四象限,不经过第三象限,
故选:C.
4.下列四组数据中,不能作为直角三角形三边长的是( )
A.1,,2 B.5,12,13 C.5,6,7 D.7,24,25
【分析】利用勾股定理逆定理进行判断即可.
解:A、12+()2=22,能构成直角三角形,故此选项不合题意;
B、52+122=132,能构成直角三角形,故此选项不符合题意;
C、52+62≠72,不能构成直角三角形,故此选项符合题意;
D、72+242=252,能构成直角三角形,故此选项不合题意.
故选:C.
5.在△ABC中和△DEF中,已知BC=EF,∠C=∠F,增加下列条件后还不能判定△ABC≌△DEF的是( )
A.AC=DF B.AB=DE C.∠A=∠D D.∠B=∠E
【分析】全等三角形的判定定理有SAS,ASA,AAS,SSS,根据定理进行判断即可.
解:
A、根据SAS即可推出△ABC≌△DEF,故本选项错误;
B、不能推出△ABC≌△DEF,故本选项正确;
C、根据AAS即可推出△ABC≌△DEF,故本选项错误;
D、根据ASA即可推出△ABC≌△DEF,故本选项错误;
故选:B.
6.∠AOB的平分线上一点P到OA的距离为4,Q是OB上任一点,则( )
A.PQ≥4 B.PQ>4 C.PQ≤4 D.PQ<4
【分析】过点P作PE⊥OB于E,根据角平分线上的点到角的两边距离相等可得PD=PE,再根据垂线段最短解答.
解:如图,过点P作PE⊥OB于E,
∵OP是∠AOB的平分线,
∴PD=PE=10,
∵Q是OB上任一点,
∴PQ≥PE,
∴PQ≥4.
故选:A.
7.已知实数x,y满足+(y+1)2=0,则x﹣y等于( )
A.1 B.﹣1 C.﹣3 D.3
【分析】根据非负数的性质列式求出x、y的值,然后代入代数式进行计算即可得解.
解:∵+(y+1)2=0,而,(y+1)2≥0,
∴x﹣2=0,y+1=0,
解得x=2,y=﹣1,
∴x﹣y=2﹣(﹣1)=2+1=3.
故选:D.
8.如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论中正确有( )
①△BPQ是等边三角形;②△PCQ是直角三角形;③∠APB=150°;④∠APC=120°.
A.①②③ B.①②④ C.②③④ D.①②③④
【分析】①根据△ABC是等边三角形,得出∠ABC=60°,根据△BQC≌△BPA,得出∠CBQ=∠ABP,PB=QB=4,PA=QC=3,∠BPA=∠BQC,求出∠PBQ=60°,即可判断①;
②根据勾股定理的逆定理即可判断得出②;
③根据△BPQ是等边三角形,△PCQ是直角三角形即可判断;
④求出∠APC=150°﹣∠QPC,和PC≠2QC,可得∠QPC≠30°,即可判断④.
解:①∵△ABC是等边三角形,
∴∠ABC=60°,
∵△BQC≌△BPA,
∴∠CBQ=∠ABP,PB=QB=4,
PA=QC=3,∠BPA=∠BQC,
∴∠PBQ=∠PBC+∠CBQ=∠PBC+∠ABP=∠ABC=60°,
∴△BPQ是等边三角形,
所以①正确;
②PQ=PB=4,
PQ2+QC2=42+32=25,
PC2=52=25,
∴PQ2+QC2=PC2,
∴∠PQC=90°,
∴△PCQ是直角三角形,
所以②正确;
③∵△BPQ是等边三角形,
∴∠PQB=∠BPQ=60°,
∴∠APB=∠BQC=∠BQP+∠PQC=60°+90°=150°,
所以③正确;
④∠APC=360°﹣150°﹣60°﹣∠QPC=150°﹣∠QPC,
∵∠PQC=90°,PC≠2QC,
∴∠QPC≠30°,
∴∠APC≠120°.
所以④错误.
所以正确的有①②③,
故选:A.
二、填空题。(本大题共有8小题,每小题3分,共24分)
9.将直线y=﹣2x向上平移1个单位长度,平移后直线的解析式为 y=﹣2x+1 .
【分析】根据一次函数图象上下平移时解析式的变化规律求解.
解:将直线y=﹣2x向上平移1个单位,得到的直线的解析式为y=﹣2x+1.
故答案为y=﹣2x+1.
10.已知,等腰三角形的两边长分别为5cm和11cm,则它的周长是 27 cm.
【分析】因为边为5cm和11cm,没说是底边还是腰,所以有两种情况,需要分类讨论.
解:当5cm为底时,
其它两边都为11cm,
5cm、11cm、11cm可以构成三角形,
周长为27cm;
当5cm为腰时,
其它两边为5cm和11cm,
∵5+5=10<11,所以不能构成三角形,故舍去,
∴答案只有27cm.
故填27.
11.在平面直角坐标系中,点(﹣3,5)关于x轴对称的点的坐标为 (﹣3,﹣5) .
【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得答案.
解:在平面直角坐标系中,点(﹣3,5)关于x轴对称的点的坐标为(﹣3,﹣5),
故答案为:(﹣3,﹣5).
12.已知y关于x的函数y=﹣x+2+m是正比例函数,则m= ﹣2 .
【分析】根据正比例函数的定义得到2+m=0,然后解方程可得m的值.
解:∵y关于x的函数y=﹣x+2+m是正比例函数,
∴2+m=0,
解得m=﹣2.
故答案为:﹣2.
13.截止北京时间2021年12月20日全球累计确诊新冠肺炎病例约为274950000例,将这个数精确到十万位为 2.750×108 例.
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,且比原数的整数位少一位;取精确度时,需要精确到哪位就数到哪位,然后根据四舍五入的原理进行取舍.
解:274950000≈2.750×108,
故选:2.750×108.
14.如图,一个正方形摆放在桌面上,那么这个正方形的边长为 .
【分析】标注字母,根据正方形的性质可得AB=AD,∠BAD=90°,再根据同角的余角相等求出∠1=∠3,然后利用“角角边”字母△ABE和△DAF全等,根据全等三角形对应边相等可得AE=DF,再利用勾股定理列式计算即可得解.
解:如图,由正方形性质可得,AB=AD,∠BAD=90°,
∴∠1+∠2=180°﹣90°=90°,
∵BE⊥AE,DF⊥AF,
∴∠AEB=90°,∠DFA=90°,
∴∠2+∠3=180°﹣90°=90°,
∴∠1=∠3,
在△ABE和△DAF中,
,
∴△ABE≌△DAF(AAS),
∴AE=DF=1,
在Rt△ABE中,AB===,
即正方形的边长为,
故答案为:.
15.已知点P(a+5,a﹣1)在第四象限,且到x轴的距离为2,则点P的坐标为 (4,﹣2) .
【分析】根据第四象限内点的坐标特征得到a+5>0,a﹣1<0,然后解不等式组即可.
解:∵点P(a+5,a﹣1)在第四象限,且到x轴的距离为2,
∴a+5>0,a﹣1<0,a﹣1=±2,
∴a=﹣1.
点P的坐标为(4,﹣2),
故答案为(4,﹣2)
16.如图,函数y=2x和y=ax+4的图象相交于点A(n,2),则不等式2x≥ax+4的解集为 x≥1 .
【分析】观察图象,写出直线y=2x没在直线y=ax+4的下方所对应的自变量的范围即可.
解:∵函数y=2x的图象经过点A(n,2),
∴2n=2,
解得:n=1,
∴点A(1,2),
当x≥1时,2x≥ax+4,
即不等式2x≥ax+4的解集为x≥1.
故答案为:x≥1.
三、解答题。(本大题共有9小题,共72分)
17.计算:
(1)(﹣2)2﹣+;
(2)﹣(π+1)0+|﹣1|.
【分析】(1)首先计算乘方、开方和开立方,然后从左向右依次计算,求出算式的值即可.
(2)首先计算零指数幂、开方和绝对值,然后从左向右依次计算,求出算式的值即可.
解:(1)(﹣2)2﹣+
=4﹣3+2
=3.
(2)﹣(π+1)0+|﹣1|
=2﹣1+(﹣1)
=1+﹣1
=.
18.求下列各式中的x:
(1)(x+2)2=25;
(2)(x﹣3)3+27=0.
【分析】(1)先直接开平方得x+2=±5,解出x;
(2)先直接开立方得x﹣3=﹣3,解出x;
解:(1)(x+2)2=25,
x+2=±5,
x1=﹣7,x2=3;
(2)(x﹣3)3+27=0,
x﹣3=﹣3,
x=0.
19.已知y﹣2与x成正比,且当x=2时,y=﹣6.
(1)求y与x之间的函数关系式;
(2)若点(a,6)在这个函数图象上,求a的值.
【分析】(1)根据题意设y﹣2=kx(k≠0),把x=2,y=﹣6代入求出k的值,即可确定出y与x的函数关系式;
(2)把(a,6)代入函数解析式求出a的值即可.
解:(1)设y﹣2=kx(k≠0),
把x=2,y=﹣6代入得:﹣6﹣2=2k,
解得:k=﹣4,
则该函数关系式为:y=﹣4x+2;
(2)∵点(a,6)在函数y=﹣4x+2图象上,
∴6=﹣4a+2,
∴a=﹣1.
20.已知:如图,点B,F,C,E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:∠B=∠E.
【分析】先证出BC=EF,∠ACB=∠DFE,再证明△ACB≌△DFE,得出对应角相等即可.
【解答】证明:∵BF=CE,
∴BC=EF,
∵AC∥DF,
∴∠ACB=∠DFE,
在△ACB和△DFE中,
,
∴△ACB≌△DFE(SAS),
∴∠B=∠E.
21.如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.CF平分∠DCE.
求证:(1)△ACD≌△BEC;
(2)CF⊥DE.
【分析】(1)根据平行线性质求出∠A=∠B,根据SAS推出即可.
(2)根据全等三角形性质推出CD=CE,根据等腰三角形性质求出即可.
【解答】证明:(1)∵AD∥BE,
∴∠A=∠B,
在△ACD和△BEC中
∴△ACD≌△BEC(SAS),
(2)∵△ACD≌△BEC,
∴CD=CE,
又∵CF平分∠DCE,
∴CF⊥DE.
22.如图,已知函数y=x+2的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,4)且与x轴及y=x+2的图象分别交于点C、D,点D的坐标为(,n).
(1)则n= ,k= ﹣2 ,b= 4 .
(2)若函数y=kx+b的函数值大于函数y=x+2的函数值,则x的取值范围是 x< .
(3)求四边形AOCD的面积.
【分析】(1)根据点D在函数y=x+2的图象上,即可求出n的值;再利用待定系数法求出k,b的值;
(2)根据图象,直接判断即可;
(3)用三角形OBC的面积减去三角形ABD的面积即可.
解:(1)∵点D(,n)在直线y=x+2上,
∴n=+2=,
∵一次函数经过点B(0,4)、点D(,),
∴,解得:,
故答案为:,﹣2,4;
(2)由图象可知,函数y=kx+b大于函数y=x+2时,图象在直线x=的左侧,
∴x<,
故答案为:x<,
(3)直线y=﹣2x+4与x轴交于点C,
∴令y=0,得:﹣2x+4=0,解得x=2,
∴点C的坐标为(2,0),
∵函数y=x+2的图象与y轴交于点A,
∴令x=0,得:y=2,
∴点A的坐标为(0,2),
S△BOC=×2×4=4,
S△BAD=×(4﹣2)×=,
∴S四边形AOCD=S△BOC﹣S△BAD=4﹣=.
23.阜宁市民广场要对如图所示的一块空地进行草坪绿化,已知AD=4m,CD=3m,AD⊥DC,AB=13m,BC=12m,绿化草坪价格150元/米2.求这块地草坪绿化的价钱.
【分析】根据勾股定理求得AC的长,再根据勾股定理的逆定理判定△ABC为直角三角形,从而不难求得这块地的面积.
解:连接AC,
∵AD⊥DC,
∴∠ADC=90°,
在Rt△ADC中,根据勾股定理,得,
AC==5,
在△ABC中,∵AC2+BC2=52+122=132=AB2,
∴△ABC是直角三角形,
∴S四边形ABCD=S△ABC﹣S△ACD
=
=24(m2),
∴这块地草坪绿化的价钱=24×150=3600(元).
24.如图,将长方形ABCD沿EF折叠,使点D与点B重合.
(1)若∠AEB=40°,求∠BFE的度数;
(2)若AB=6,AD=18,求CF的长.
【分析】(1)根据平角的定义和折叠的性质即可得到结论;
(2)首先设CF=x,则FG=CF=x,BF=BC﹣CF=18﹣x,然后在直角△BGF利用勾股定理求出x即可.
解:(1)∵∠AEB=40°,
∴∠BED=180°﹣∠AEB=140°,
∵将长方形ABCD沿EF折叠,使点D与点B重合,
∴∠BEF=∠DEF=BED=70°,
∵AD∥BC,
∴∠BFE=∠DEF=70°;
(2)设CF=x,则FG=CF=x,BF=BC﹣CF=18﹣x,
∵将长方形ABCD沿EF折叠,使点D与点B重合,
∴∠G=∠C=90°,BG=CD=AB=6,
在Rt△BGF中,BG2+GF2=BF2,
则62+x2=(18﹣x)2,
解得:x=8.
∴CF=8.
25.如图,一次函数y=ax+b与正比例函数y=kx的图象交于点M.
(1)求正比例函数和一次函数的解析式;
(2)根据图象,写出关于x的不等式kx>ax+b的解集;
(3)求△MOP的面积.
【分析】(1)先利用待定系数法求出一次函数解析式,再利用一次函数解析式确定M点的坐标,然后根据待定系数法求出正比例函数解析式;
(2)结合图象写出正比例函数图象在直线y=ax+b的上方所对应的自变量的范围即可;
(3)先利用一次函数解析式求出P点坐标,然后利用三角形面积公式.
解:(1)∵y=ax+b经过(1,0)和(0,﹣2),
∴,解得k=2,b=﹣2,
∴一次函数表达式为:y=2x﹣2
∵点M在该一次函数图象上,
∴m=2×2﹣2=2,则M点坐标为(2,2);
又∵M在函数y=kx图象上,
∴2k=2,解得k=1,
∴正比例函数的解析式为y=x;
(2)由图象可知,x<2时,x>2x﹣2
(3)当y=0时,2x﹣2=0,解得x=1,则P(1,0),
∴S△MOP=×1×2=1.
同课章节目录
