2021-2022学年安徽省合肥市庐江县八年级(上)期末数学试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年安徽省合肥市庐江县八年级(上)期末数学试卷(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 813.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 10:58:02 | ||
图片预览




文档简介
2021-2022学年安徽省合肥市庐江县八年级第一学期期末数学试卷
一、选择题(本题共10小题,每小题4分,满分40分。请将每小题唯一正确选项前的代号填入下面的答题栏内)
1.下列微信表情图标属于轴对称图形的是( )
A. B. C. D.
2.若一个三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能为( )
A.1cm B.2cm C.5cm D.8cm
3.某种细胞的直径是0.00000095米,将0.00000095米用科学记数法表示为( )
A.9.5×10﹣7 B.9.5×10﹣8 C.0.95×10﹣7 D.95×10﹣8
4.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=24°,则∠2的度数是( )
A.54° B.48° C.46° D.76°
5.若x2+2(m﹣1)x+16是完全平方式,则m的值为( )
A.±8 B.﹣3或5 C.﹣3 D.5
6.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( )
A.SAS B.ASA C.AAS D.SSS
7.△ABC中,AB=4,∠B=∠C=15°,则△ABC的面积是( )
A.2 B.4 C.6 D.8
8.下列计算正确的是( )
A.x3÷x3=0 B.(﹣3x)2=6x2 C.2x﹣2= D.(x3)2=x6
9.△ABC中,AB=AC,CD为AB上的高,且△ADC为等腰三角形,则∠BCD等于( )
A.67.5° B.22.5°
C.45° D.67.5°或22.5°
10.元旦期间,庐江某商城生意火爆.元月1日,某商品的售价是m元/千克,元月2日,该商品的售价调整为n元/千克(m≠n),顾客甲1日和2日分别购买2千克的该商品;顾客乙1日与2日分别购买20元的该商品.在这两次购物中,顾客甲、乙购买该商品的平均单价谁划算( )
A.甲划算 B.乙划算 C.一样划算 D.无法比较
二、填空题(本题共4小题,每小题5分,满分20分)
11.化简:= .
12.因式分解:3ab2﹣6ab+3a= .
13.一个多边形的内角和是外角和的3倍,则这个多边形的边数是 .
14.如图,在四边形ABCD中,∠BAD=121°,∠B=∠D=90°,点M、N分别在BC、CD上,
(1)当∠MAN=∠C时,∠AMN+∠ANM= °;
(2)当△AMN周长最小时,∠AMN+∠ANM= °.
三、(本题共2小题,每小题8分,满分16分)
15.计算:.
16.化简:(3m+n)2﹣3m(m+2n).
四、(本题共2小题,每小题8分,满分16分)
17.如图,AB与CD交于点E,点E是AB的中点,∠A=∠B.试说明:AC=BD.
18.如图,从边长为a的正方形纸片中剪掉一个边长为b的正方形纸片(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)探究:上述操作能验证的等式是 .
(2)应用:利用(1)中得出的等式,计算:.
五、(本题共2小题,每小题10分,满分20分)
19.先化简:,再从2,﹣2,3,﹣3中选一个合适的数作为a的值代入求值.
20.如图,在平面直角坐标系中,△ABC的各顶点坐标分别为A(4,﹣4),B(1,﹣1),C(3,﹣1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)直接写出点A1,B1,C1的坐标;
(3)在△A1B1C1中,求∠A1B1C1的度数.
六、(本题满分12分)
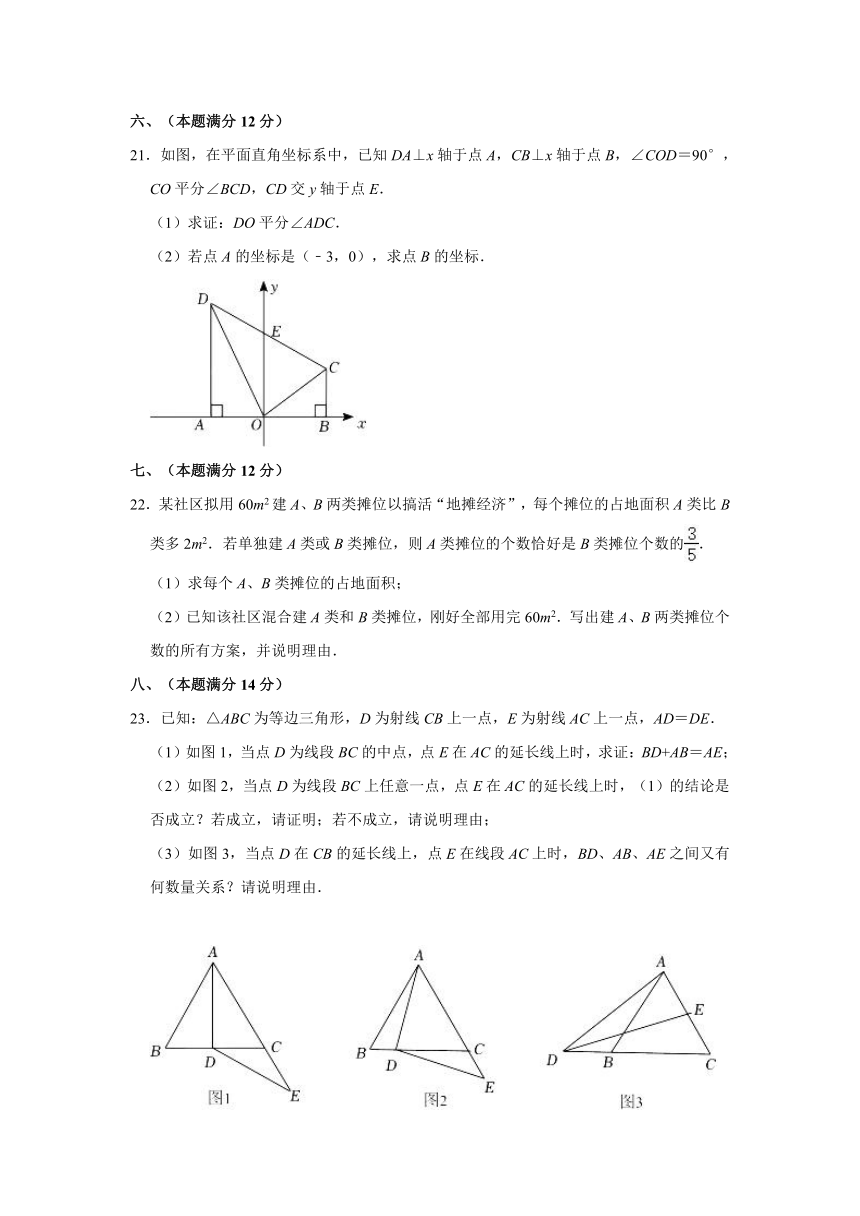
21.如图,在平面直角坐标系中,已知DA⊥x轴于点A,CB⊥x轴于点B,∠COD=90°,CO平分∠BCD,CD交y轴于点E.
(1)求证:DO平分∠ADC.
(2)若点A的坐标是(﹣3,0),求点B的坐标.
七、(本题满分12分)
22.某社区拟用60m2建A、B两类摊位以搞活“地摊经济”,每个摊位的占地面积A类比B类多2m2.若单独建A类或B类摊位,则A类摊位的个数恰好是B类摊位个数的.
(1)求每个A、B类摊位的占地面积;
(2)已知该社区混合建A类和B类摊位,刚好全部用完60m2.写出建A、B两类摊位个数的所有方案,并说明理由.
八、(本题满分14分)
23.已知:△ABC为等边三角形,D为射线CB上一点,E为射线AC上一点,AD=DE.
(1)如图1,当点D为线段BC的中点,点E在AC的延长线上时,求证:BD+AB=AE;
(2)如图2,当点D为线段BC上任意一点,点E在AC的延长线上时,(1)的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)如图3,当点D在CB的延长线上,点E在线段AC上时,BD、AB、AE之间又有何数量关系?请说明理由.
参考答案
一、选择题(本题共10小题,每小题4分,满分40分。请将每小题唯一正确选项前的代号填入下面的答题栏内)
1.下列微信表情图标属于轴对称图形的是( )
A. B. C. D.
【分析】结合轴对称图形的概念求解即可.
解:A、不是轴对称图形,本选项不合题意;
B、不是轴对称图形,本选项不合题意;
C、是轴对称图形,本选项符合题意;
D、不是轴对称图形,本选项不合题意.
故选:C.
2.若一个三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能为( )
A.1cm B.2cm C.5cm D.8cm
【分析】设第三边为xcm,再根据三角形的三边关系求出x的取值范围,选出合适的x的值即可.
解:设第三边为xcm,
∵三角形的两边长分别为3cm和5cm,
∴5cm﹣3cm<x<5cm+3cm,即2cm<x<8cm,
∴5cm符合题意,
故选:C.
3.某种细胞的直径是0.00000095米,将0.00000095米用科学记数法表示为( )
A.9.5×10﹣7 B.9.5×10﹣8 C.0.95×10﹣7 D.95×10﹣8
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.00000095=9.5×10﹣7,
故选:A.
4.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=24°,则∠2的度数是( )
A.54° B.48° C.46° D.76°
【分析】首先根据三角形外角的性质求出∠BEF的度数,再根据平行线的性质得到∠2的度数.
解:∵∠BEF是△AEF的外角,∠1=24°,∠F=30°,
∴∠BEF=∠1+∠F=54°,
∵AB∥CD,
∴∠2=∠BEF=54°.
故选:A.
5.若x2+2(m﹣1)x+16是完全平方式,则m的值为( )
A.±8 B.﹣3或5 C.﹣3 D.5
【分析】由于x2+2(m﹣1)x+16是完全平方式,而16=42,然后根据完全平方公式即可得到关于m的方程,解方程即可求解.
解:∵x2+2(m﹣1)x+16是完全平方式,而16=42,
∴m﹣1=4或m﹣1=﹣4,
∴m=5或﹣3.
故选:B.
6.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( )
A.SAS B.ASA C.AAS D.SSS
【分析】如图,由作图可知,OA=OB=CE=EF,BA=CF.根据SSS证明△AOB≌△CEF.
解:如图,由作图可知,OA=OB=CE=EF,BA=CF.
在△AOB和△CEF中,
,
∴△AOB≌△CEF(SSS),
故选:D.
7.△ABC中,AB=4,∠B=∠C=15°,则△ABC的面积是( )
A.2 B.4 C.6 D.8
【分析】据三角形的一个外角等于与它不相邻的两个内角的和求出∠CAD的度数,然后根据30°角所对的直角边等于斜边的一半求解即可.
解:∵AB=4,∠B=∠C=15°,
∴AB=AC=4,
过C作CD⊥AB交BA的延长线于D,
∵∠B=∠ACB=15°,
∴∠CAD=∠B+∠ACB=15°+15°=30°,
∵AC=4,CD是AB边上的高,
∴CD=AC=×4=2,
∴S△ABC=×4×2=4,
故选:B.
8.下列计算正确的是( )
A.x3÷x3=0 B.(﹣3x)2=6x2 C.2x﹣2= D.(x3)2=x6
【分析】直接利用同底数幂的乘除运算法则以及积的乘方运算法则、负整数指数幂的性质分别化简得出答案.
解:A、x3÷x3=1,故此选项错误;
B、(﹣3x)2=9x2,故此选项错误;
C、2x﹣2=,故此选项错误;
D、(x3)2=x6,故此选项正确.
故选:D.
9.△ABC中,AB=AC,CD为AB上的高,且△ADC为等腰三角形,则∠BCD等于( )
A.67.5° B.22.5°
C.45° D.67.5°或22.5°
【分析】根据题意,应该考虑两种情况,①CD在△ABC内部;②CD在△ABC外部.分别结合已知条件进行计算即可.
解:①如右图所示,CD在△ABC内部,
∵AB=AC,CD为AB上的高,
∴∠B=∠ACB,∠CDB=90°,
又∵△ADC是等腰三角形,
∴∠DAC=∠DCA=45°,
∴∠B=∠ACB=(180°﹣45°)=67.5°,
∴∠BCD=∠ACB﹣ACD=67.5°﹣45°=22.5°;
②如右图所示,CD在△ABC外部,
∵AB=AC,CD为AB上的高,
∴∠B=∠ACB,∠CDB=90°,
又∵△ADC是等腰三角形,
∴∠DAC=∠DCA=45°,
∴∠B=∠ACB=×45°=22.5°,
∴∠BCD=∠ACB+ACD=22.5°+45°=67.5°;
故答案是22.5°或67.5°.
故选:D.
10.元旦期间,庐江某商城生意火爆.元月1日,某商品的售价是m元/千克,元月2日,该商品的售价调整为n元/千克(m≠n),顾客甲1日和2日分别购买2千克的该商品;顾客乙1日与2日分别购买20元的该商品.在这两次购物中,顾客甲、乙购买该商品的平均单价谁划算( )
A.甲划算 B.乙划算 C.一样划算 D.无法比较
【分析】根据加权平均数的公式分别表示出顾客甲、乙购买该商品的平均单价,再利用作差法比较大小即可.
解:∵顾客甲购买该商品的平均单价为=(元/千克),
顾客甲购买该商品的平均单价为=(元/千克),
∴﹣==>0,
∴乙划算.
故选:B.
二、填空题(本题共4小题,每小题5分,满分20分)
11.化简:= .
【分析】直接利用分式的性质化简进而得出答案.
解:=.
故答案为:.
12.因式分解:3ab2﹣6ab+3a= 3a(b﹣1)2 .
【分析】先提取公因式,然后利用完全平方公式进行因式分解.
解:原式=3a(b2﹣2b+1)
=3a(b﹣1)2.
故答案为:3a(b﹣1)2.
13.一个多边形的内角和是外角和的3倍,则这个多边形的边数是 八 .
【分析】根据多边形的内角和定理,多边形的内角和等于(n﹣2) 180°,外角和等于360°,然后列方程求解即可.
解:设多边形的边数是n,根据题意得,
(n﹣2) 180°=3×360°,
解得n=8,
∴这个多边形为八边形.
故答案为:八.
14.如图,在四边形ABCD中,∠BAD=121°,∠B=∠D=90°,点M、N分别在BC、CD上,
(1)当∠MAN=∠C时,∠AMN+∠ANM= 121 °;
(2)当△AMN周长最小时,∠AMN+∠ANM= 118 °.
【分析】(1)由三角形内角和定理求出∠C=180°﹣121°=69°,所以∠MAN=∠C=69°,即可求出AMN+∠ANM.
(2)作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,利用三角形内角和定理即可.
解:(1)∵∠BAD=121°,∠B=∠D=90°,
∴∠C=180°﹣121°=69°,
∴∠MAN=∠C=69°,
∴AMN+∠ANM=180°﹣∠MAN=180°﹣69°=121°,
故答案为121.
(2)如下图,作A关于BC和CD的对称点A′,A″,
连接A′A″,交BC于M,交CD于N,
则A′A″即为△AMN的周长最小值.
作DA延长线AH,
∵∠DAB=121°,
∴∠HAA′=59°,
∴∠AA′M+∠A″=∠HAA′=59°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,
∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM
=∠MA′A+∠MAA′+∠NAD+∠A″
=2(∠AA′M+∠A″)=2×59°=118°.
故答案为:118.
三、(本题共2小题,每小题8分,满分16分)
15.计算:.
【分析】化简零指数幂,负整数指数幂,然后再计算.
解:原式=1﹣4
=﹣3.
16.化简:(3m+n)2﹣3m(m+2n).
【分析】原式利用完全平方公式,以及单项式乘多项式法则计算,去括号合并即可得到结果.
解:原式=(9m2+6mn+n2)﹣(3m2+6mn)
=9m2+6mn+n2﹣3m2﹣6mn
=6m2+n2.
四、(本题共2小题,每小题8分,满分16分)
17.如图,AB与CD交于点E,点E是AB的中点,∠A=∠B.试说明:AC=BD.
【分析】证明△AEC≌△BED(ASA),可得AC=BD.
【解答】证明:∵E是AB的中点,
∴AE=BE,
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA),
∴AC=BD.
18.如图,从边长为a的正方形纸片中剪掉一个边长为b的正方形纸片(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)探究:上述操作能验证的等式是 a2﹣b2=(a+b)(a﹣b) .
(2)应用:利用(1)中得出的等式,计算:.
【分析】(1)分别计算图1和图2中阴影部分的面积,根据面积相等即可得出答案;
(2)逆用平方差公式,中间项全部约分掉,只剩下第一项和最后一项,从而得出答案.
解:(1)第一个图形中阴影部分的面积是a2﹣b2,
第二个图形的面积是(a+b)(a﹣b),
则a2﹣b2=(a+b)(a﹣b).
故答案为:a2﹣b2=(a+b)(a﹣b);
(2)原式=(1﹣)(1+)(1﹣)(1+) (1﹣)(1+)
=×××× ××
=.
五、(本题共2小题,每小题10分,满分20分)
19.先化简:,再从2,﹣2,3,﹣3中选一个合适的数作为a的值代入求值.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再根据分式有意义的条件得出a的值,继而代入计算即可.
解:原式=÷(﹣)
=
=﹣,
∵a﹣2≠0,a﹣3≠0,a+3≠0,
∴a≠2,a≠±3,
∴当a=﹣2时,原式=﹣=﹣.
20.如图,在平面直角坐标系中,△ABC的各顶点坐标分别为A(4,﹣4),B(1,﹣1),C(3,﹣1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)直接写出点A1,B1,C1的坐标;
(3)在△A1B1C1中,求∠A1B1C1的度数.
【分析】(1)根据轴对称的性质分别作出A,B,C的对应点A1,B1,C1即可;
(2)根据点A1,B1,C1的位置写出坐标即可;
(3)利用网格特征解决问题即可.
解:(1)如图,△A1B1C1即为所求;
(2)点A1,(4,4),B1(1,1),C1(3,1);
(3)∠A1B1C1=45°.
六、(本题满分12分)
21.如图,在平面直角坐标系中,已知DA⊥x轴于点A,CB⊥x轴于点B,∠COD=90°,CO平分∠BCD,CD交y轴于点E.
(1)求证:DO平分∠ADC.
(2)若点A的坐标是(﹣3,0),求点B的坐标.
【分析】(1)先由DA⊥x轴、CB⊥x轴得到DA∥CB∥y轴,进而得到∠ADO=∠ODE、∠EOC=∠OCB,再由∠COD=90°得到∠DOE+∠EOC=90°和∠ODE+∠DCO=90°,然后得到∠EOD=∠EDO,从而得到∠ADO=∠EDO,即可得证DO平分∠ADC;
(2)过点O作OF⊥CD于点F,然后由角平分线的性质定理得到OA=OF、OF=OB,再由点A(﹣3,0)求得点B的坐标.
【解答】(1)证明:∵CO平分∠BCD,
∴∠DCO=∠BCO,
∵CB⊥x轴,DA⊥x轴,
∴DA∥CB∥y轴,
∴∠BCO=∠EOC,∠ADO=∠EOD,
∴∠EOC=∠DCO,
∵∠COD=90°,
∴∠DCO+∠ODC=90°,∠EOC+∠EOD=90°,
∴∠EOD=∠EDO,
∴∠EDO=∠ADO,
∴DO平分∠ADC.
(2)解:过点O作OF⊥CD于点F,则∠OFD=∠OFC=90°,
∵DO平分∠ADC,CO平分∠DCB,OA⊥AD,OB⊥CB,
∴OA=OF,OF=OB,
∴OA=OB,
∵A(﹣3,0),
∴OB=OA=3,
∴B(3,0).
七、(本题满分12分)
22.某社区拟用60m2建A、B两类摊位以搞活“地摊经济”,每个摊位的占地面积A类比B类多2m2.若单独建A类或B类摊位,则A类摊位的个数恰好是B类摊位个数的.
(1)求每个A、B类摊位的占地面积;
(2)已知该社区混合建A类和B类摊位,刚好全部用完60m2.写出建A、B两类摊位个数的所有方案,并说明理由.
【分析】(1)设每个B类摊位的占地面积为xm2,则每个A类摊位的占地面积为(x+2)m2,由题意:社区拟用60m2建A、B两类摊位以搞活“地摊经济”,若单独建A类或B类摊位,则A类摊位的个数恰好是B类摊位个数的.列出分式方程,解方程即可;
(2)设建造a个A类摊位,b个B类摊位,由题意:该社区混合建A类和B类摊位,刚好全部用完60m2.列出二元一次方程,求其正整数解即可.
解:(1)设每个B类摊位的占地面积为xm2,则每个A类摊位的占地面积为(x+2)m2,
依题意得:=×,
解得:x=3,
经检验,x=3是原方程的解,且符合题意,
∴x+2=5.
答:每个A类摊位的占地面积为5m2,每个B类摊位的占地面积为3m2.
(2)有3个方案,理由如下:
设建造a个A类摊位,b个B类摊位,
由题意得:5a+3b=60,
则a=12﹣b,
∵a、b为正整数,
∴或或,
∴共有3个方案:
①A类摊位9个,B类摊位5个;
②A类摊位6个,B类摊位10个;
③A类摊位3个,B类摊位15个.
八、(本题满分14分)
23.已知:△ABC为等边三角形,D为射线CB上一点,E为射线AC上一点,AD=DE.
(1)如图1,当点D为线段BC的中点,点E在AC的延长线上时,求证:BD+AB=AE;
(2)如图2,当点D为线段BC上任意一点,点E在AC的延长线上时,(1)的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)如图3,当点D在CB的延长线上,点E在线段AC上时,BD、AB、AE之间又有何数量关系?请说明理由.
【分析】(1)如图1,利用△ABC是等边三角形得出角,边关系,利用AD=DE,得出△CDE是等腰三角形,得出CD=CE,由线段关系可得出BD+AB=AE;
(2)如图2,在AB上取BH=BD,连接DH,利用AHD≌△DCE得出DH=CE,得出AE=AB+BD;
(3)如图3,在AB上取AF=AE,连接DF,EF,利用△AFD≌△EFD得出角的关系,得出△BDF是等腰三角形,根据边的关系得出结论AB=BD+AE.
【解答】证明:(1)如图1,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠B=∠ACB=60°,
∵点D为线段BC的中点,
∴BD=CD,∠CAD=∠BAC=30°,
∵AD=DE,
∴∠E=∠CAD=30°,
∵∠ACB=∠E+∠CDE,
∴∠CDE=60°﹣30°=30°,
∴∠CDE=∠E,
∴CD=CE,
∴AE=AC+CE=AB+CD=AB+BD;
(2)成立,理由如下:
如图2,在AB上取BH=BD,连接DH,
∵BH=BD,∠B=60°,
∴△BDH为等边三角形,
∴∠BHD=60°,BD=DH,
∵AB﹣BH=BC﹣BD,即AH=DC,
∵AD=DE,
∴∠E=∠CAD,
∴∠BAC﹣∠CAD=∠ACB﹣∠E,即∠BAD=∠CDE,
∵∠BHD=60°,∠ACB=60°,
∴180°﹣∠BHD=180°﹣∠ACB,即∠AHD=∠DCE,
在△AHD和△DCE,
,
∴△AHD≌△DCE(AAS),
∴DH=CE,
∴BD=CE,
∴AE=AC+CE=AB+BD;
(3)AB=BD+AE,理由如下:
如图3,在AB上取AF=AE,连接DF,EF,
∵△ABC为等边三角形,
∴∠BAC=∠ABC=60°,
∴△AFE是等边三角形,
∴∠FAE=∠FEA=∠AFE=60°,
∴EF∥BC,
∴∠EDB=∠DEF,
在△AFD和△EFD中,
,
∴△AFD≌△EFD(SSS),
∴∠ADF=∠EDF,∠DAF=∠DEF,
∴∠FDB=∠EDF+∠EDB,∠DFB=∠DAF+∠ADF,
∵∠EDB=∠DEF,
∴∠FDB=∠DFB,
∴DB=BF,
∵AB=AF+FB,
∴AB=BD+AE.
一、选择题(本题共10小题,每小题4分,满分40分。请将每小题唯一正确选项前的代号填入下面的答题栏内)
1.下列微信表情图标属于轴对称图形的是( )
A. B. C. D.
2.若一个三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能为( )
A.1cm B.2cm C.5cm D.8cm
3.某种细胞的直径是0.00000095米,将0.00000095米用科学记数法表示为( )
A.9.5×10﹣7 B.9.5×10﹣8 C.0.95×10﹣7 D.95×10﹣8
4.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=24°,则∠2的度数是( )
A.54° B.48° C.46° D.76°
5.若x2+2(m﹣1)x+16是完全平方式,则m的值为( )
A.±8 B.﹣3或5 C.﹣3 D.5
6.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( )
A.SAS B.ASA C.AAS D.SSS
7.△ABC中,AB=4,∠B=∠C=15°,则△ABC的面积是( )
A.2 B.4 C.6 D.8
8.下列计算正确的是( )
A.x3÷x3=0 B.(﹣3x)2=6x2 C.2x﹣2= D.(x3)2=x6
9.△ABC中,AB=AC,CD为AB上的高,且△ADC为等腰三角形,则∠BCD等于( )
A.67.5° B.22.5°
C.45° D.67.5°或22.5°
10.元旦期间,庐江某商城生意火爆.元月1日,某商品的售价是m元/千克,元月2日,该商品的售价调整为n元/千克(m≠n),顾客甲1日和2日分别购买2千克的该商品;顾客乙1日与2日分别购买20元的该商品.在这两次购物中,顾客甲、乙购买该商品的平均单价谁划算( )
A.甲划算 B.乙划算 C.一样划算 D.无法比较
二、填空题(本题共4小题,每小题5分,满分20分)
11.化简:= .
12.因式分解:3ab2﹣6ab+3a= .
13.一个多边形的内角和是外角和的3倍,则这个多边形的边数是 .
14.如图,在四边形ABCD中,∠BAD=121°,∠B=∠D=90°,点M、N分别在BC、CD上,
(1)当∠MAN=∠C时,∠AMN+∠ANM= °;
(2)当△AMN周长最小时,∠AMN+∠ANM= °.
三、(本题共2小题,每小题8分,满分16分)
15.计算:.
16.化简:(3m+n)2﹣3m(m+2n).
四、(本题共2小题,每小题8分,满分16分)
17.如图,AB与CD交于点E,点E是AB的中点,∠A=∠B.试说明:AC=BD.
18.如图,从边长为a的正方形纸片中剪掉一个边长为b的正方形纸片(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)探究:上述操作能验证的等式是 .
(2)应用:利用(1)中得出的等式,计算:.
五、(本题共2小题,每小题10分,满分20分)
19.先化简:,再从2,﹣2,3,﹣3中选一个合适的数作为a的值代入求值.
20.如图,在平面直角坐标系中,△ABC的各顶点坐标分别为A(4,﹣4),B(1,﹣1),C(3,﹣1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)直接写出点A1,B1,C1的坐标;
(3)在△A1B1C1中,求∠A1B1C1的度数.
六、(本题满分12分)
21.如图,在平面直角坐标系中,已知DA⊥x轴于点A,CB⊥x轴于点B,∠COD=90°,CO平分∠BCD,CD交y轴于点E.
(1)求证:DO平分∠ADC.
(2)若点A的坐标是(﹣3,0),求点B的坐标.
七、(本题满分12分)
22.某社区拟用60m2建A、B两类摊位以搞活“地摊经济”,每个摊位的占地面积A类比B类多2m2.若单独建A类或B类摊位,则A类摊位的个数恰好是B类摊位个数的.
(1)求每个A、B类摊位的占地面积;
(2)已知该社区混合建A类和B类摊位,刚好全部用完60m2.写出建A、B两类摊位个数的所有方案,并说明理由.
八、(本题满分14分)
23.已知:△ABC为等边三角形,D为射线CB上一点,E为射线AC上一点,AD=DE.
(1)如图1,当点D为线段BC的中点,点E在AC的延长线上时,求证:BD+AB=AE;
(2)如图2,当点D为线段BC上任意一点,点E在AC的延长线上时,(1)的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)如图3,当点D在CB的延长线上,点E在线段AC上时,BD、AB、AE之间又有何数量关系?请说明理由.
参考答案
一、选择题(本题共10小题,每小题4分,满分40分。请将每小题唯一正确选项前的代号填入下面的答题栏内)
1.下列微信表情图标属于轴对称图形的是( )
A. B. C. D.
【分析】结合轴对称图形的概念求解即可.
解:A、不是轴对称图形,本选项不合题意;
B、不是轴对称图形,本选项不合题意;
C、是轴对称图形,本选项符合题意;
D、不是轴对称图形,本选项不合题意.
故选:C.
2.若一个三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能为( )
A.1cm B.2cm C.5cm D.8cm
【分析】设第三边为xcm,再根据三角形的三边关系求出x的取值范围,选出合适的x的值即可.
解:设第三边为xcm,
∵三角形的两边长分别为3cm和5cm,
∴5cm﹣3cm<x<5cm+3cm,即2cm<x<8cm,
∴5cm符合题意,
故选:C.
3.某种细胞的直径是0.00000095米,将0.00000095米用科学记数法表示为( )
A.9.5×10﹣7 B.9.5×10﹣8 C.0.95×10﹣7 D.95×10﹣8
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.00000095=9.5×10﹣7,
故选:A.
4.如图,将直尺与含30°角的三角尺摆放在一起,若∠1=24°,则∠2的度数是( )
A.54° B.48° C.46° D.76°
【分析】首先根据三角形外角的性质求出∠BEF的度数,再根据平行线的性质得到∠2的度数.
解:∵∠BEF是△AEF的外角,∠1=24°,∠F=30°,
∴∠BEF=∠1+∠F=54°,
∵AB∥CD,
∴∠2=∠BEF=54°.
故选:A.
5.若x2+2(m﹣1)x+16是完全平方式,则m的值为( )
A.±8 B.﹣3或5 C.﹣3 D.5
【分析】由于x2+2(m﹣1)x+16是完全平方式,而16=42,然后根据完全平方公式即可得到关于m的方程,解方程即可求解.
解:∵x2+2(m﹣1)x+16是完全平方式,而16=42,
∴m﹣1=4或m﹣1=﹣4,
∴m=5或﹣3.
故选:B.
6.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( )
A.SAS B.ASA C.AAS D.SSS
【分析】如图,由作图可知,OA=OB=CE=EF,BA=CF.根据SSS证明△AOB≌△CEF.
解:如图,由作图可知,OA=OB=CE=EF,BA=CF.
在△AOB和△CEF中,
,
∴△AOB≌△CEF(SSS),
故选:D.
7.△ABC中,AB=4,∠B=∠C=15°,则△ABC的面积是( )
A.2 B.4 C.6 D.8
【分析】据三角形的一个外角等于与它不相邻的两个内角的和求出∠CAD的度数,然后根据30°角所对的直角边等于斜边的一半求解即可.
解:∵AB=4,∠B=∠C=15°,
∴AB=AC=4,
过C作CD⊥AB交BA的延长线于D,
∵∠B=∠ACB=15°,
∴∠CAD=∠B+∠ACB=15°+15°=30°,
∵AC=4,CD是AB边上的高,
∴CD=AC=×4=2,
∴S△ABC=×4×2=4,
故选:B.
8.下列计算正确的是( )
A.x3÷x3=0 B.(﹣3x)2=6x2 C.2x﹣2= D.(x3)2=x6
【分析】直接利用同底数幂的乘除运算法则以及积的乘方运算法则、负整数指数幂的性质分别化简得出答案.
解:A、x3÷x3=1,故此选项错误;
B、(﹣3x)2=9x2,故此选项错误;
C、2x﹣2=,故此选项错误;
D、(x3)2=x6,故此选项正确.
故选:D.
9.△ABC中,AB=AC,CD为AB上的高,且△ADC为等腰三角形,则∠BCD等于( )
A.67.5° B.22.5°
C.45° D.67.5°或22.5°
【分析】根据题意,应该考虑两种情况,①CD在△ABC内部;②CD在△ABC外部.分别结合已知条件进行计算即可.
解:①如右图所示,CD在△ABC内部,
∵AB=AC,CD为AB上的高,
∴∠B=∠ACB,∠CDB=90°,
又∵△ADC是等腰三角形,
∴∠DAC=∠DCA=45°,
∴∠B=∠ACB=(180°﹣45°)=67.5°,
∴∠BCD=∠ACB﹣ACD=67.5°﹣45°=22.5°;
②如右图所示,CD在△ABC外部,
∵AB=AC,CD为AB上的高,
∴∠B=∠ACB,∠CDB=90°,
又∵△ADC是等腰三角形,
∴∠DAC=∠DCA=45°,
∴∠B=∠ACB=×45°=22.5°,
∴∠BCD=∠ACB+ACD=22.5°+45°=67.5°;
故答案是22.5°或67.5°.
故选:D.
10.元旦期间,庐江某商城生意火爆.元月1日,某商品的售价是m元/千克,元月2日,该商品的售价调整为n元/千克(m≠n),顾客甲1日和2日分别购买2千克的该商品;顾客乙1日与2日分别购买20元的该商品.在这两次购物中,顾客甲、乙购买该商品的平均单价谁划算( )
A.甲划算 B.乙划算 C.一样划算 D.无法比较
【分析】根据加权平均数的公式分别表示出顾客甲、乙购买该商品的平均单价,再利用作差法比较大小即可.
解:∵顾客甲购买该商品的平均单价为=(元/千克),
顾客甲购买该商品的平均单价为=(元/千克),
∴﹣==>0,
∴乙划算.
故选:B.
二、填空题(本题共4小题,每小题5分,满分20分)
11.化简:= .
【分析】直接利用分式的性质化简进而得出答案.
解:=.
故答案为:.
12.因式分解:3ab2﹣6ab+3a= 3a(b﹣1)2 .
【分析】先提取公因式,然后利用完全平方公式进行因式分解.
解:原式=3a(b2﹣2b+1)
=3a(b﹣1)2.
故答案为:3a(b﹣1)2.
13.一个多边形的内角和是外角和的3倍,则这个多边形的边数是 八 .
【分析】根据多边形的内角和定理,多边形的内角和等于(n﹣2) 180°,外角和等于360°,然后列方程求解即可.
解:设多边形的边数是n,根据题意得,
(n﹣2) 180°=3×360°,
解得n=8,
∴这个多边形为八边形.
故答案为:八.
14.如图,在四边形ABCD中,∠BAD=121°,∠B=∠D=90°,点M、N分别在BC、CD上,
(1)当∠MAN=∠C时,∠AMN+∠ANM= 121 °;
(2)当△AMN周长最小时,∠AMN+∠ANM= 118 °.
【分析】(1)由三角形内角和定理求出∠C=180°﹣121°=69°,所以∠MAN=∠C=69°,即可求出AMN+∠ANM.
(2)作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,利用三角形内角和定理即可.
解:(1)∵∠BAD=121°,∠B=∠D=90°,
∴∠C=180°﹣121°=69°,
∴∠MAN=∠C=69°,
∴AMN+∠ANM=180°﹣∠MAN=180°﹣69°=121°,
故答案为121.
(2)如下图,作A关于BC和CD的对称点A′,A″,
连接A′A″,交BC于M,交CD于N,
则A′A″即为△AMN的周长最小值.
作DA延长线AH,
∵∠DAB=121°,
∴∠HAA′=59°,
∴∠AA′M+∠A″=∠HAA′=59°,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,
∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM
=∠MA′A+∠MAA′+∠NAD+∠A″
=2(∠AA′M+∠A″)=2×59°=118°.
故答案为:118.
三、(本题共2小题,每小题8分,满分16分)
15.计算:.
【分析】化简零指数幂,负整数指数幂,然后再计算.
解:原式=1﹣4
=﹣3.
16.化简:(3m+n)2﹣3m(m+2n).
【分析】原式利用完全平方公式,以及单项式乘多项式法则计算,去括号合并即可得到结果.
解:原式=(9m2+6mn+n2)﹣(3m2+6mn)
=9m2+6mn+n2﹣3m2﹣6mn
=6m2+n2.
四、(本题共2小题,每小题8分,满分16分)
17.如图,AB与CD交于点E,点E是AB的中点,∠A=∠B.试说明:AC=BD.
【分析】证明△AEC≌△BED(ASA),可得AC=BD.
【解答】证明:∵E是AB的中点,
∴AE=BE,
在△AEC和△BED中,
,
∴△AEC≌△BED(ASA),
∴AC=BD.
18.如图,从边长为a的正方形纸片中剪掉一个边长为b的正方形纸片(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)探究:上述操作能验证的等式是 a2﹣b2=(a+b)(a﹣b) .
(2)应用:利用(1)中得出的等式,计算:.
【分析】(1)分别计算图1和图2中阴影部分的面积,根据面积相等即可得出答案;
(2)逆用平方差公式,中间项全部约分掉,只剩下第一项和最后一项,从而得出答案.
解:(1)第一个图形中阴影部分的面积是a2﹣b2,
第二个图形的面积是(a+b)(a﹣b),
则a2﹣b2=(a+b)(a﹣b).
故答案为:a2﹣b2=(a+b)(a﹣b);
(2)原式=(1﹣)(1+)(1﹣)(1+) (1﹣)(1+)
=×××× ××
=.
五、(本题共2小题,每小题10分,满分20分)
19.先化简:,再从2,﹣2,3,﹣3中选一个合适的数作为a的值代入求值.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再根据分式有意义的条件得出a的值,继而代入计算即可.
解:原式=÷(﹣)
=
=﹣,
∵a﹣2≠0,a﹣3≠0,a+3≠0,
∴a≠2,a≠±3,
∴当a=﹣2时,原式=﹣=﹣.
20.如图,在平面直角坐标系中,△ABC的各顶点坐标分别为A(4,﹣4),B(1,﹣1),C(3,﹣1).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)直接写出点A1,B1,C1的坐标;
(3)在△A1B1C1中,求∠A1B1C1的度数.
【分析】(1)根据轴对称的性质分别作出A,B,C的对应点A1,B1,C1即可;
(2)根据点A1,B1,C1的位置写出坐标即可;
(3)利用网格特征解决问题即可.
解:(1)如图,△A1B1C1即为所求;
(2)点A1,(4,4),B1(1,1),C1(3,1);
(3)∠A1B1C1=45°.
六、(本题满分12分)
21.如图,在平面直角坐标系中,已知DA⊥x轴于点A,CB⊥x轴于点B,∠COD=90°,CO平分∠BCD,CD交y轴于点E.
(1)求证:DO平分∠ADC.
(2)若点A的坐标是(﹣3,0),求点B的坐标.
【分析】(1)先由DA⊥x轴、CB⊥x轴得到DA∥CB∥y轴,进而得到∠ADO=∠ODE、∠EOC=∠OCB,再由∠COD=90°得到∠DOE+∠EOC=90°和∠ODE+∠DCO=90°,然后得到∠EOD=∠EDO,从而得到∠ADO=∠EDO,即可得证DO平分∠ADC;
(2)过点O作OF⊥CD于点F,然后由角平分线的性质定理得到OA=OF、OF=OB,再由点A(﹣3,0)求得点B的坐标.
【解答】(1)证明:∵CO平分∠BCD,
∴∠DCO=∠BCO,
∵CB⊥x轴,DA⊥x轴,
∴DA∥CB∥y轴,
∴∠BCO=∠EOC,∠ADO=∠EOD,
∴∠EOC=∠DCO,
∵∠COD=90°,
∴∠DCO+∠ODC=90°,∠EOC+∠EOD=90°,
∴∠EOD=∠EDO,
∴∠EDO=∠ADO,
∴DO平分∠ADC.
(2)解:过点O作OF⊥CD于点F,则∠OFD=∠OFC=90°,
∵DO平分∠ADC,CO平分∠DCB,OA⊥AD,OB⊥CB,
∴OA=OF,OF=OB,
∴OA=OB,
∵A(﹣3,0),
∴OB=OA=3,
∴B(3,0).
七、(本题满分12分)
22.某社区拟用60m2建A、B两类摊位以搞活“地摊经济”,每个摊位的占地面积A类比B类多2m2.若单独建A类或B类摊位,则A类摊位的个数恰好是B类摊位个数的.
(1)求每个A、B类摊位的占地面积;
(2)已知该社区混合建A类和B类摊位,刚好全部用完60m2.写出建A、B两类摊位个数的所有方案,并说明理由.
【分析】(1)设每个B类摊位的占地面积为xm2,则每个A类摊位的占地面积为(x+2)m2,由题意:社区拟用60m2建A、B两类摊位以搞活“地摊经济”,若单独建A类或B类摊位,则A类摊位的个数恰好是B类摊位个数的.列出分式方程,解方程即可;
(2)设建造a个A类摊位,b个B类摊位,由题意:该社区混合建A类和B类摊位,刚好全部用完60m2.列出二元一次方程,求其正整数解即可.
解:(1)设每个B类摊位的占地面积为xm2,则每个A类摊位的占地面积为(x+2)m2,
依题意得:=×,
解得:x=3,
经检验,x=3是原方程的解,且符合题意,
∴x+2=5.
答:每个A类摊位的占地面积为5m2,每个B类摊位的占地面积为3m2.
(2)有3个方案,理由如下:
设建造a个A类摊位,b个B类摊位,
由题意得:5a+3b=60,
则a=12﹣b,
∵a、b为正整数,
∴或或,
∴共有3个方案:
①A类摊位9个,B类摊位5个;
②A类摊位6个,B类摊位10个;
③A类摊位3个,B类摊位15个.
八、(本题满分14分)
23.已知:△ABC为等边三角形,D为射线CB上一点,E为射线AC上一点,AD=DE.
(1)如图1,当点D为线段BC的中点,点E在AC的延长线上时,求证:BD+AB=AE;
(2)如图2,当点D为线段BC上任意一点,点E在AC的延长线上时,(1)的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)如图3,当点D在CB的延长线上,点E在线段AC上时,BD、AB、AE之间又有何数量关系?请说明理由.
【分析】(1)如图1,利用△ABC是等边三角形得出角,边关系,利用AD=DE,得出△CDE是等腰三角形,得出CD=CE,由线段关系可得出BD+AB=AE;
(2)如图2,在AB上取BH=BD,连接DH,利用AHD≌△DCE得出DH=CE,得出AE=AB+BD;
(3)如图3,在AB上取AF=AE,连接DF,EF,利用△AFD≌△EFD得出角的关系,得出△BDF是等腰三角形,根据边的关系得出结论AB=BD+AE.
【解答】证明:(1)如图1,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠B=∠ACB=60°,
∵点D为线段BC的中点,
∴BD=CD,∠CAD=∠BAC=30°,
∵AD=DE,
∴∠E=∠CAD=30°,
∵∠ACB=∠E+∠CDE,
∴∠CDE=60°﹣30°=30°,
∴∠CDE=∠E,
∴CD=CE,
∴AE=AC+CE=AB+CD=AB+BD;
(2)成立,理由如下:
如图2,在AB上取BH=BD,连接DH,
∵BH=BD,∠B=60°,
∴△BDH为等边三角形,
∴∠BHD=60°,BD=DH,
∵AB﹣BH=BC﹣BD,即AH=DC,
∵AD=DE,
∴∠E=∠CAD,
∴∠BAC﹣∠CAD=∠ACB﹣∠E,即∠BAD=∠CDE,
∵∠BHD=60°,∠ACB=60°,
∴180°﹣∠BHD=180°﹣∠ACB,即∠AHD=∠DCE,
在△AHD和△DCE,
,
∴△AHD≌△DCE(AAS),
∴DH=CE,
∴BD=CE,
∴AE=AC+CE=AB+BD;
(3)AB=BD+AE,理由如下:
如图3,在AB上取AF=AE,连接DF,EF,
∵△ABC为等边三角形,
∴∠BAC=∠ABC=60°,
∴△AFE是等边三角形,
∴∠FAE=∠FEA=∠AFE=60°,
∴EF∥BC,
∴∠EDB=∠DEF,
在△AFD和△EFD中,
,
∴△AFD≌△EFD(SSS),
∴∠ADF=∠EDF,∠DAF=∠DEF,
∴∠FDB=∠EDF+∠EDB,∠DFB=∠DAF+∠ADF,
∵∠EDB=∠DEF,
∴∠FDB=∠DFB,
∴DB=BF,
∵AB=AF+FB,
∴AB=BD+AE.
同课章节目录
