2021-2022学年上海市普陀区某校七年级(上)期末数学试卷(Word版含解析)
文档属性
| 名称 | 2021-2022学年上海市普陀区某校七年级(上)期末数学试卷(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 662.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 11:04:22 | ||
图片预览




文档简介
2021-2022学年上海市普陀区某校七年级第一学期期末数学试卷
一、选择题(本大题共有6题,每题2分,满分12分)
1.下列计算结果中,正确的是( )
A.a3+a3=a6 B.(2a)3=6a3
C.(a﹣7)2=a2﹣49 D.a7÷a6=a.
2.下列说法中正确的是( )
A.是整式
B.多项式2x2﹣y2+xy﹣4x3y3按字母x升幂排列为﹣4x3y3+2x2+xy﹣y2
C.2x是一次单项式
D.a3b+2a2b﹣3ab的二次项系数是3
3.下列各式从左到右的变形是因式分解的是( )
A.1+2x+3x2=1+x(2+3x)
B.3x(x+y)=3x2+3xy
C.6a2b+3ab2﹣ab=ab(6a+3b﹣1)
D.12a3x5=4ax2﹣3a2x3
4.当x=3时,下列各式值为0的是( )
A. B. C. D.
5.由圆和正五边形所组成的图形如图所示,那么这个图形( )
A.是轴对称图形但不是中心对称图形
B.是中心对称图形但不是轴对称图形
C.既是中心对称图形又是轴对称图形
D.既不是中心对称图形也不是轴对称图形
6.如果2(5﹣a)(6+a)=100,那么a2+a+1的值为( )
A.19 B.﹣19 C.69 D.﹣69
二、填空题(本大题共有12题,每题3分,满分36分)
7.用代数式表示“x的2倍与y的差”为 .
8.计算:(﹣a2) a3= .
9.计算:(x+3)(x+5)= .
10.计算:(9a6﹣12a3)÷3a3= .
11.因式分解:ax﹣by+ay﹣bx= .
12.因式分解:2x2﹣8= .
13.新型冠状病毒颗粒呈球形或者椭圆形,传染性非常强,传播速度非常快,它的直径约为125纳米(0.000000125米)左右,将0.000000125用科学记数法表示为 .
14.计算:()﹣2= .
15.计算:= .
16.已知关于x的多项式x2+kx﹣3能分解成两个一次多项式的积,那么整数k的值为 .
17.如图,正方形ABCD的边AB在数轴上,数轴上点B表示的数为1,正方形ABCD的面积为a2(a>1).将正方形ABCD在数轴上向右水平移动,移动后的正方形记为A′B′C′D′,点A、B、C、D的对应点分别为A′、B′、C′、D′,移动后的正方形A′B′C′D′与原正方形ABCD重叠部分图形的面积记为S.当S=a时,数轴上点B′表示的数是 (用含a的代数式表示).
18.如图,在△ABC中,∠ACB=50°,将△ABC绕点C逆时针旋转得到△DEC(点D、E分别与点A、B对应),如果∠ACD与∠ACE的度数之比为3:2,当旋转角大于0°且小于180°时,旋转角的度数为 .
三、简答题(本大题共有6题,每题4分,满分24分)
19.计算:(a﹣b)2﹣(2a﹣b)(2a+b).
20.计算:()﹣1﹣.
21.因式分解:(x2+4x)2﹣(x2+4x)﹣20.
22.因式分解:1﹣a2﹣4b2+4ab.
23.已知3m=4,3n=5,分别求3m+n与32m﹣n的值.
24.解方程:1+=.
四、解答题(第25、26每题6分,第27、28每题8分,满分28分)
25.如图,已知四边形ABCD和直线MN.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O成中心对称;
(3)四边形A1B1C1D1与四边形A2B2C2D2的位置关系是 .
26.2022年北京冬奥会开幕在即,参加女子1500米短道速滑的运动员在教练员的指导下努力训练提高竞技水平.在经过指导后,甲运动员的速度是原来的1.1倍,时间缩短了15秒,那么经过指导后,甲运动员的速度是多少?
27.先化简,再求值:÷(﹣x﹣2),其中x=﹣2.
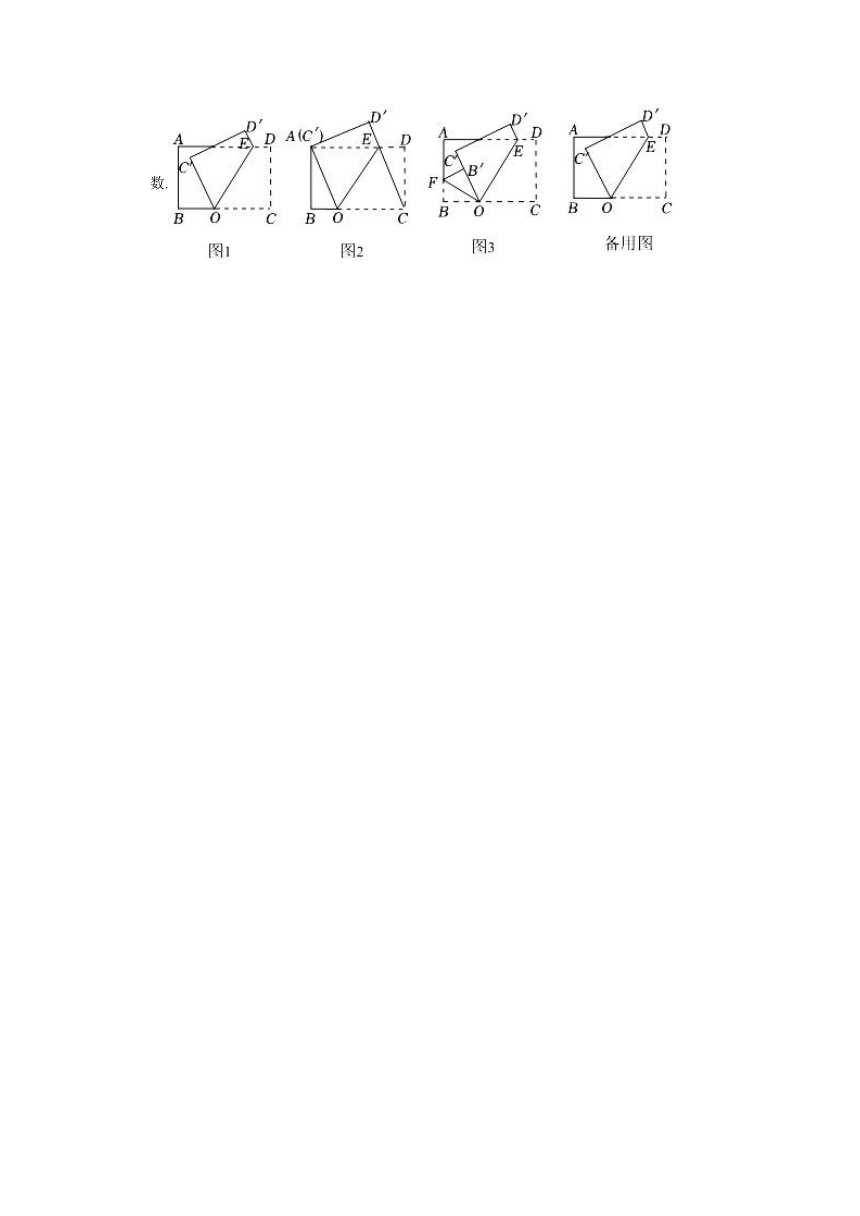
28.如图1,长方形纸片ABCD(AD>AB),点O位于边BC上,点E位于边AD上,将纸片沿OE折叠,点C、D的对应点分别为点C′、D′.
(1)当点C′与点A重合时,如图2,如果AD=12,CD=8,联结CE,那么△CDE的周长是 ;
(2)如果点F位于边AB上,将纸片沿OF折叠,点B的对应点为点B′.
①当点B′恰好落在线段OC′上时,如图3,那么∠EOF的度数为 ;(直接填写答案)
②当∠B′OC′=20°时,作出图形,并写出∠EOF的度数.
参考答案
一、选择题(本大题共有6题,每题2分,满分12分)
1.下列计算结果中,正确的是( )
A.a3+a3=a6 B.(2a)3=6a3
C.(a﹣7)2=a2﹣49 D.a7÷a6=a.
【分析】根据合并同类项法则、积的乘方的运算法则、完全平方公式、同底数幂的除法的运算法则直接计算得出结果即可得出答案.
解:A、a3+a3=2a3,原计算错误,故此选项不符合题意;
B、(2a)3=8a3,原计算错误,故此选项不符合题意;
C、(a﹣7)2=a2﹣14a+49,原计算错误,故此选项不符合题意;
D、a7÷a6=a,原计算正确,故此选项符合题意.
故选:D.
2.下列说法中正确的是( )
A.是整式
B.多项式2x2﹣y2+xy﹣4x3y3按字母x升幂排列为﹣4x3y3+2x2+xy﹣y2
C.2x是一次单项式
D.a3b+2a2b﹣3ab的二次项系数是3
【分析】根据整式的定义即可判断选项A,先按x的指数从小到大的顺序排列,再判断选项B即可,根据单项式的定义和单项式的次数定义即可判断选项C,根据单项式的系数和次数的定义即可判断选项D.
解:A.分母中含有字母,是分式,不是整式,故本选项不符合题意;
B.多项式2x2﹣y2+xy﹣4x3y3按字母x升幂排列为﹣y2+xy+2x2﹣4x3y3,故本选项不符合题意;
C.2x是一次单项式,故本选项符合题意;
D.a3b+2a2b﹣3ab的二次项系数是﹣3,故本选项不符合题意;
故选:C.
3.下列各式从左到右的变形是因式分解的是( )
A.1+2x+3x2=1+x(2+3x)
B.3x(x+y)=3x2+3xy
C.6a2b+3ab2﹣ab=ab(6a+3b﹣1)
D.12a3x5=4ax2﹣3a2x3
【分析】根据因式分解的定义逐个判断即可.
解:A.从左到右的变形不属于因式分解,故本选项不符合题意;
B.从左到右的变形属于整式乘法,不属于因式分解,故本选项不符合题意;
C.从左到右的变形属于因式分解,故本选项符合题意;
D.从左到右的变形不属于因式分解,故本选项不符合题意;
故选:C.
4.当x=3时,下列各式值为0的是( )
A. B. C. D.
【分析】将x=3代入分式,然后根据分式有意义的条件(分母不能为零)和分式值为零的条件(分子为零,且分母不为零)进行分析判断.
解:A、当x=3时,3﹣x=0,原分式没有意义,故此选项不符合题意;
B、当x=3时,x2﹣9=0,x+3≠0,原分式的值为0,故此选项符合题意;
C、当x=3时,x﹣3=0,原分式没有意义,故此选项不符合题意;
D、当x=3时,x2﹣9=0,原分式没有意义,故此选项不符合题意;
故选:B.
5.由圆和正五边形所组成的图形如图所示,那么这个图形( )
A.是轴对称图形但不是中心对称图形
B.是中心对称图形但不是轴对称图形
C.既是中心对称图形又是轴对称图形
D.既不是中心对称图形也不是轴对称图形
【分析】直接利用中心对称图形以及轴对称图形的定义进而判断得出答案.
解:此图形是轴对称图形但并不是中心对称图形.
故选:A.
6.如果2(5﹣a)(6+a)=100,那么a2+a+1的值为( )
A.19 B.﹣19 C.69 D.﹣69
【分析】先根据多项式乘以多项式法则计算2(5﹣a)(6+a)=100,得:a2+a=﹣20,最后整体代入可得结论.
解:∵2(5﹣a)(6+a)=100,
∴﹣a2+5a﹣6a+30=50,
∴a2+a=﹣20,
∴a2+a+1=﹣20+1=﹣19.
故选:B.
二、填空题(本大题共有12题,每题3分,满分36分)
7.用代数式表示“x的2倍与y的差”为 2x﹣y .
【分析】根据题意可以用代数式表示出x的2倍与y的差.
解:用代数式表示“x的2倍与y的差”为:2x﹣y,
故答案为:2x﹣y.
8.计算:(﹣a2) a3= ﹣a5 .
【分析】同底数幂相乘,底数不变,指数相加.
解:原式=﹣a5,
故答案是﹣a5.
9.计算:(x+3)(x+5)= x2+8x+15 .
【分析】根据多项式与多项式相乘的法则计算.
解:(x+3)(x+5)
=x2+5x+3x+15
=x2+8x+15;
故答案为:x2+8x+15.
10.计算:(9a6﹣12a3)÷3a3= 3a3﹣4 .
【分析】直接利用整式的除法运算法则计算得出答案.
解:(9a6﹣12a3)÷3a3
=9a6÷3a3﹣12a3÷3a3
=3a3﹣4.
故答案为:3a3﹣4.
11.因式分解:ax﹣by+ay﹣bx= (a﹣b)(x+y) .
【分析】先分组,再提取公因式,再提取公因式.
解:ax﹣by+ay﹣bx
=(ax﹣bx)+(ay﹣by)
=x(a﹣b)+y(a﹣b)
=(a﹣b)(x+y).
故答案为:(a﹣b)(x+y).
12.因式分解:2x2﹣8= 2(x+2)(x﹣2) .
【分析】观察原式,找到公因式2,提出后,再利用平方差公式分解即可得出答案.
解:2x2﹣8=2(x+2)(x﹣2).
13.新型冠状病毒颗粒呈球形或者椭圆形,传染性非常强,传播速度非常快,它的直径约为125纳米(0.000000125米)左右,将0.000000125用科学记数法表示为 1.25×10﹣7 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
解:0.000000125=1.25×10﹣7.
故答案为:1.25×10﹣7.
14.计算:()﹣2= 9 .
【分析】根据负整数指数幂的意义,a﹣n=,(a≠0),即可判断.
解:()﹣2===9.
故答案是:9.
15.计算:= .
【分析】根据分式加减法的法则计算,即可得出结果.
解:
=
=
=,
故答案为:.
16.已知关于x的多项式x2+kx﹣3能分解成两个一次多项式的积,那么整数k的值为 ±2 .
【分析】把常数项分解成两个整数的乘积,k就等于那两个整数之和.
解:∵﹣3=﹣3×1或﹣3=﹣1×3,
∴k=﹣3+1=﹣2或k=﹣1+3=2,
∴整数k的值为:±2,
故答案为:±2.
17.如图,正方形ABCD的边AB在数轴上,数轴上点B表示的数为1,正方形ABCD的面积为a2(a>1).将正方形ABCD在数轴上向右水平移动,移动后的正方形记为A′B′C′D′,点A、B、C、D的对应点分别为A′、B′、C′、D′,移动后的正方形A′B′C′D′与原正方形ABCD重叠部分图形的面积记为S.当S=a时,数轴上点B′表示的数是 a (用含a的代数式表示).
【分析】根据正方形的面积得到正方形的边长,当S=a时得到AB′=1,求出BB′,根据点B表示的数为1即可得到点B′表示的数.
解:如图,
∵正方形ABCD的面积为a2,
∴正方形ABCD的边长为a,
∵移动后的正方形A′B′C′D′与原正方形ABCD重叠部分图形的面积记为S,
当S=a时,a AB′=a,
∴AB′=1,
∴BB′=AB﹣AB′=a﹣1,
∵点B表示的数为1,
∴点B′表示的数为1+a﹣1=a,
故答案为:a.
18.如图,在△ABC中,∠ACB=50°,将△ABC绕点C逆时针旋转得到△DEC(点D、E分别与点A、B对应),如果∠ACD与∠ACE的度数之比为3:2,当旋转角大于0°且小于180°时,旋转角的度数为 30°或150° .
【分析】分两种情况:当旋转角小于50°时和当旋转角大于50°时,分别画出图形,由∠ACD与∠ACE的度数之比为3:2,求出∠ACE,即可得到旋转角度数.
解:当旋转角小于50°时,如图:
∵∠ACB=50°,△ABC绕点C逆时针旋转得到△DEC,
∴∠DCE=50°,
∵∠ACD与∠ACE的度数之比为3:2,
∴∠ACE=×50°=20°,
∴旋转角∠BCE=∠ACB﹣∠ACE=30°,
当旋转角大于50°时,如图:
∵∠ACD与∠ACE的度数之比为3:2,∠DCE=∠ACB=50°,
∴∠ACE=2∠DCE=100°,
∴旋转角∠BCE=∠ACB+∠ACE=150°,
故答案为:30°或150°.
三、简答题(本大题共有6题,每题4分,满分24分)
19.计算:(a﹣b)2﹣(2a﹣b)(2a+b).
【分析】根据完全平方公式和平方差公式化简即可.
解:原式=a2﹣2ab+b2﹣(4a2﹣b2)
=a2﹣2ab+b2﹣4a2+b2
=﹣3a2﹣2ab+2b2.
20.计算:()﹣1﹣.
【分析】根据负整数指数幂、分式的除法和减法可以解答本题.
解:()﹣1﹣
=﹣
=﹣
=
=
=
=.
21.因式分解:(x2+4x)2﹣(x2+4x)﹣20.
【分析】直接利用十字相乘法分解因式得出即可.
解:原式=(x2+4x﹣5)(x2+4x+4)
=(x+5)(x﹣1)(x+2)2.
22.因式分解:1﹣a2﹣4b2+4ab.
【分析】先分组,再逆用完全平方公式、平方差公式进行因式分解.
解:1﹣a2﹣4b2+4ab
=1﹣(a2+4b2﹣4ab)
=1﹣(a﹣2b)2
=(1+a﹣2b)[1﹣(a﹣2b)]
=(1+a﹣2b)(1﹣a+2b).
23.已知3m=4,3n=5,分别求3m+n与32m﹣n的值.
【分析】利用同底数幂的乘法的法则,同底数幂的除法的法则,幂的乘方的法则对所求的式子进行整理,再代入运算即可.
解:当3m=4,3n=5时,
3m+n
=3m×3n
=4×5
=20;
32m﹣n
=32m÷3n
=(3m)2÷3n
=42÷5
=16÷5
=.
24.解方程:1+=.
【分析】按照解分式方程的步骤进行计算即可解答.
解:1+=,
1﹣x2+1=x(1﹣x),
解得:x=2,
检验:当x=2时,1﹣x2≠0,
∴x=2是原方程的根.
四、解答题(第25、26每题6分,第27、28每题8分,满分28分)
25.如图,已知四边形ABCD和直线MN.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O成中心对称;
(3)四边形A1B1C1D1与四边形A2B2C2D2的位置关系是 CO .
【分析】(1)根据轴对称的性质即可画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)根据中心对称性质即可画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O成中心对称;
(3)结合以上画图即可得四边形A1B1C1D1与四边形A2B2C2D2的位置关系是.
解:(1)如图,A1B1C1D1即为所求;
(2)如图,A2B2C2D2即为所求;
(3)关于直线CO成轴对称.
故答案为:CO.
26.2022年北京冬奥会开幕在即,参加女子1500米短道速滑的运动员在教练员的指导下努力训练提高竞技水平.在经过指导后,甲运动员的速度是原来的1.1倍,时间缩短了15秒,那么经过指导后,甲运动员的速度是多少?
【分析】设甲运动员原来的速度是x米/秒,则经过指导后的速度是1.1x米/秒,利用时间=路程÷速度,结合经过指导后时间缩短了15秒,即可得出关于x的分式方程,解之经检验后可得出甲运动员原来的速度,再将其代入1.1x中即可求出经过指导后甲运动员的速度.
解:设甲运动员原来的速度是x米/秒,则经过指导后的速度是1.1x米/秒,
依题意得:﹣=15,
解得:x=,
经检验,x=是原方程的解,且符合题意,
∴1.1x=1.1×=10.
答:经过指导后,甲运动员的速度是10米/秒.
27.先化简,再求值:÷(﹣x﹣2),其中x=﹣2.
【分析】原式小括号内的式子进行通分计算,然后再算括号外面的除法,最后代入求值.
解:原式=÷[﹣]
=÷
=
=,
当x=﹣2时,原式===.
28.如图1,长方形纸片ABCD(AD>AB),点O位于边BC上,点E位于边AD上,将纸片沿OE折叠,点C、D的对应点分别为点C′、D′.
(1)当点C′与点A重合时,如图2,如果AD=12,CD=8,联结CE,那么△CDE的周长是 20 ;
(2)如果点F位于边AB上,将纸片沿OF折叠,点B的对应点为点B′.
①当点B′恰好落在线段OC′上时,如图3,那么∠EOF的度数为 90° ;(直接填写答案)
②当∠B′OC′=20°时,作出图形,并写出∠EOF的度数.
【分析】(1)证明DE+EC=AD=12,可得结论;
(2)①利用角平分线的定义以及平角的性质解决问题即可;
②分两种情形,分别画出图形,利用角平分线的定义,平角的性质解决问题即可.
解:(1)如图2中,点C′与点A重合时,
由翻折的性质可知,EA=EC,
∴DE+EC=DE+EA=AD=12,
∴△CDE的周长=DE+EC+CD=12+8=20.
故答案为:20;
(2)①如图3中,
由翻折的性质可知,∠BOF=∠B′OF,∠EOC=∠EOC′,
∵∠BOC=180°,
∴∠EOF=∠EOB′+∠FOB′=(∠COB′+∠BOB′)=∠BOC=90°.
故答案为:90°;
②如图4﹣1中,当OB′值OC′的下方时,
∵∠B′OC′=20°,
∴∠BOB′+∠COC′=180°﹣20°=160°,
∵∠FOB′=∠BOB′,∠EOC′=∠COC′,
∴∠FOB′+∠EOC′=×160°=80°,
∴∠EOF=∠FOB′+∠EOC′+∠B′OC′=100°.
如图4﹣2中,当OB′在OC′的上方时,
∵∠B′OC′=20°,
∴∠BOB′+∠COC′=180°+20°=200°,
∵∠FOB′=∠BOB′,∠EOC′=∠COC′,
∴∠FOB′+∠EOC′=×200°=100°,
∴∠EOF=∠FOB′+∠EOC′﹣∠B′OC′=80°.
综上所述,∠EOF的度数为100°或80°.
一、选择题(本大题共有6题,每题2分,满分12分)
1.下列计算结果中,正确的是( )
A.a3+a3=a6 B.(2a)3=6a3
C.(a﹣7)2=a2﹣49 D.a7÷a6=a.
2.下列说法中正确的是( )
A.是整式
B.多项式2x2﹣y2+xy﹣4x3y3按字母x升幂排列为﹣4x3y3+2x2+xy﹣y2
C.2x是一次单项式
D.a3b+2a2b﹣3ab的二次项系数是3
3.下列各式从左到右的变形是因式分解的是( )
A.1+2x+3x2=1+x(2+3x)
B.3x(x+y)=3x2+3xy
C.6a2b+3ab2﹣ab=ab(6a+3b﹣1)
D.12a3x5=4ax2﹣3a2x3
4.当x=3时,下列各式值为0的是( )
A. B. C. D.
5.由圆和正五边形所组成的图形如图所示,那么这个图形( )
A.是轴对称图形但不是中心对称图形
B.是中心对称图形但不是轴对称图形
C.既是中心对称图形又是轴对称图形
D.既不是中心对称图形也不是轴对称图形
6.如果2(5﹣a)(6+a)=100,那么a2+a+1的值为( )
A.19 B.﹣19 C.69 D.﹣69
二、填空题(本大题共有12题,每题3分,满分36分)
7.用代数式表示“x的2倍与y的差”为 .
8.计算:(﹣a2) a3= .
9.计算:(x+3)(x+5)= .
10.计算:(9a6﹣12a3)÷3a3= .
11.因式分解:ax﹣by+ay﹣bx= .
12.因式分解:2x2﹣8= .
13.新型冠状病毒颗粒呈球形或者椭圆形,传染性非常强,传播速度非常快,它的直径约为125纳米(0.000000125米)左右,将0.000000125用科学记数法表示为 .
14.计算:()﹣2= .
15.计算:= .
16.已知关于x的多项式x2+kx﹣3能分解成两个一次多项式的积,那么整数k的值为 .
17.如图,正方形ABCD的边AB在数轴上,数轴上点B表示的数为1,正方形ABCD的面积为a2(a>1).将正方形ABCD在数轴上向右水平移动,移动后的正方形记为A′B′C′D′,点A、B、C、D的对应点分别为A′、B′、C′、D′,移动后的正方形A′B′C′D′与原正方形ABCD重叠部分图形的面积记为S.当S=a时,数轴上点B′表示的数是 (用含a的代数式表示).
18.如图,在△ABC中,∠ACB=50°,将△ABC绕点C逆时针旋转得到△DEC(点D、E分别与点A、B对应),如果∠ACD与∠ACE的度数之比为3:2,当旋转角大于0°且小于180°时,旋转角的度数为 .
三、简答题(本大题共有6题,每题4分,满分24分)
19.计算:(a﹣b)2﹣(2a﹣b)(2a+b).
20.计算:()﹣1﹣.
21.因式分解:(x2+4x)2﹣(x2+4x)﹣20.
22.因式分解:1﹣a2﹣4b2+4ab.
23.已知3m=4,3n=5,分别求3m+n与32m﹣n的值.
24.解方程:1+=.
四、解答题(第25、26每题6分,第27、28每题8分,满分28分)
25.如图,已知四边形ABCD和直线MN.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O成中心对称;
(3)四边形A1B1C1D1与四边形A2B2C2D2的位置关系是 .
26.2022年北京冬奥会开幕在即,参加女子1500米短道速滑的运动员在教练员的指导下努力训练提高竞技水平.在经过指导后,甲运动员的速度是原来的1.1倍,时间缩短了15秒,那么经过指导后,甲运动员的速度是多少?
27.先化简,再求值:÷(﹣x﹣2),其中x=﹣2.
28.如图1,长方形纸片ABCD(AD>AB),点O位于边BC上,点E位于边AD上,将纸片沿OE折叠,点C、D的对应点分别为点C′、D′.
(1)当点C′与点A重合时,如图2,如果AD=12,CD=8,联结CE,那么△CDE的周长是 ;
(2)如果点F位于边AB上,将纸片沿OF折叠,点B的对应点为点B′.
①当点B′恰好落在线段OC′上时,如图3,那么∠EOF的度数为 ;(直接填写答案)
②当∠B′OC′=20°时,作出图形,并写出∠EOF的度数.
参考答案
一、选择题(本大题共有6题,每题2分,满分12分)
1.下列计算结果中,正确的是( )
A.a3+a3=a6 B.(2a)3=6a3
C.(a﹣7)2=a2﹣49 D.a7÷a6=a.
【分析】根据合并同类项法则、积的乘方的运算法则、完全平方公式、同底数幂的除法的运算法则直接计算得出结果即可得出答案.
解:A、a3+a3=2a3,原计算错误,故此选项不符合题意;
B、(2a)3=8a3,原计算错误,故此选项不符合题意;
C、(a﹣7)2=a2﹣14a+49,原计算错误,故此选项不符合题意;
D、a7÷a6=a,原计算正确,故此选项符合题意.
故选:D.
2.下列说法中正确的是( )
A.是整式
B.多项式2x2﹣y2+xy﹣4x3y3按字母x升幂排列为﹣4x3y3+2x2+xy﹣y2
C.2x是一次单项式
D.a3b+2a2b﹣3ab的二次项系数是3
【分析】根据整式的定义即可判断选项A,先按x的指数从小到大的顺序排列,再判断选项B即可,根据单项式的定义和单项式的次数定义即可判断选项C,根据单项式的系数和次数的定义即可判断选项D.
解:A.分母中含有字母,是分式,不是整式,故本选项不符合题意;
B.多项式2x2﹣y2+xy﹣4x3y3按字母x升幂排列为﹣y2+xy+2x2﹣4x3y3,故本选项不符合题意;
C.2x是一次单项式,故本选项符合题意;
D.a3b+2a2b﹣3ab的二次项系数是﹣3,故本选项不符合题意;
故选:C.
3.下列各式从左到右的变形是因式分解的是( )
A.1+2x+3x2=1+x(2+3x)
B.3x(x+y)=3x2+3xy
C.6a2b+3ab2﹣ab=ab(6a+3b﹣1)
D.12a3x5=4ax2﹣3a2x3
【分析】根据因式分解的定义逐个判断即可.
解:A.从左到右的变形不属于因式分解,故本选项不符合题意;
B.从左到右的变形属于整式乘法,不属于因式分解,故本选项不符合题意;
C.从左到右的变形属于因式分解,故本选项符合题意;
D.从左到右的变形不属于因式分解,故本选项不符合题意;
故选:C.
4.当x=3时,下列各式值为0的是( )
A. B. C. D.
【分析】将x=3代入分式,然后根据分式有意义的条件(分母不能为零)和分式值为零的条件(分子为零,且分母不为零)进行分析判断.
解:A、当x=3时,3﹣x=0,原分式没有意义,故此选项不符合题意;
B、当x=3时,x2﹣9=0,x+3≠0,原分式的值为0,故此选项符合题意;
C、当x=3时,x﹣3=0,原分式没有意义,故此选项不符合题意;
D、当x=3时,x2﹣9=0,原分式没有意义,故此选项不符合题意;
故选:B.
5.由圆和正五边形所组成的图形如图所示,那么这个图形( )
A.是轴对称图形但不是中心对称图形
B.是中心对称图形但不是轴对称图形
C.既是中心对称图形又是轴对称图形
D.既不是中心对称图形也不是轴对称图形
【分析】直接利用中心对称图形以及轴对称图形的定义进而判断得出答案.
解:此图形是轴对称图形但并不是中心对称图形.
故选:A.
6.如果2(5﹣a)(6+a)=100,那么a2+a+1的值为( )
A.19 B.﹣19 C.69 D.﹣69
【分析】先根据多项式乘以多项式法则计算2(5﹣a)(6+a)=100,得:a2+a=﹣20,最后整体代入可得结论.
解:∵2(5﹣a)(6+a)=100,
∴﹣a2+5a﹣6a+30=50,
∴a2+a=﹣20,
∴a2+a+1=﹣20+1=﹣19.
故选:B.
二、填空题(本大题共有12题,每题3分,满分36分)
7.用代数式表示“x的2倍与y的差”为 2x﹣y .
【分析】根据题意可以用代数式表示出x的2倍与y的差.
解:用代数式表示“x的2倍与y的差”为:2x﹣y,
故答案为:2x﹣y.
8.计算:(﹣a2) a3= ﹣a5 .
【分析】同底数幂相乘,底数不变,指数相加.
解:原式=﹣a5,
故答案是﹣a5.
9.计算:(x+3)(x+5)= x2+8x+15 .
【分析】根据多项式与多项式相乘的法则计算.
解:(x+3)(x+5)
=x2+5x+3x+15
=x2+8x+15;
故答案为:x2+8x+15.
10.计算:(9a6﹣12a3)÷3a3= 3a3﹣4 .
【分析】直接利用整式的除法运算法则计算得出答案.
解:(9a6﹣12a3)÷3a3
=9a6÷3a3﹣12a3÷3a3
=3a3﹣4.
故答案为:3a3﹣4.
11.因式分解:ax﹣by+ay﹣bx= (a﹣b)(x+y) .
【分析】先分组,再提取公因式,再提取公因式.
解:ax﹣by+ay﹣bx
=(ax﹣bx)+(ay﹣by)
=x(a﹣b)+y(a﹣b)
=(a﹣b)(x+y).
故答案为:(a﹣b)(x+y).
12.因式分解:2x2﹣8= 2(x+2)(x﹣2) .
【分析】观察原式,找到公因式2,提出后,再利用平方差公式分解即可得出答案.
解:2x2﹣8=2(x+2)(x﹣2).
13.新型冠状病毒颗粒呈球形或者椭圆形,传染性非常强,传播速度非常快,它的直径约为125纳米(0.000000125米)左右,将0.000000125用科学记数法表示为 1.25×10﹣7 .
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
解:0.000000125=1.25×10﹣7.
故答案为:1.25×10﹣7.
14.计算:()﹣2= 9 .
【分析】根据负整数指数幂的意义,a﹣n=,(a≠0),即可判断.
解:()﹣2===9.
故答案是:9.
15.计算:= .
【分析】根据分式加减法的法则计算,即可得出结果.
解:
=
=
=,
故答案为:.
16.已知关于x的多项式x2+kx﹣3能分解成两个一次多项式的积,那么整数k的值为 ±2 .
【分析】把常数项分解成两个整数的乘积,k就等于那两个整数之和.
解:∵﹣3=﹣3×1或﹣3=﹣1×3,
∴k=﹣3+1=﹣2或k=﹣1+3=2,
∴整数k的值为:±2,
故答案为:±2.
17.如图,正方形ABCD的边AB在数轴上,数轴上点B表示的数为1,正方形ABCD的面积为a2(a>1).将正方形ABCD在数轴上向右水平移动,移动后的正方形记为A′B′C′D′,点A、B、C、D的对应点分别为A′、B′、C′、D′,移动后的正方形A′B′C′D′与原正方形ABCD重叠部分图形的面积记为S.当S=a时,数轴上点B′表示的数是 a (用含a的代数式表示).
【分析】根据正方形的面积得到正方形的边长,当S=a时得到AB′=1,求出BB′,根据点B表示的数为1即可得到点B′表示的数.
解:如图,
∵正方形ABCD的面积为a2,
∴正方形ABCD的边长为a,
∵移动后的正方形A′B′C′D′与原正方形ABCD重叠部分图形的面积记为S,
当S=a时,a AB′=a,
∴AB′=1,
∴BB′=AB﹣AB′=a﹣1,
∵点B表示的数为1,
∴点B′表示的数为1+a﹣1=a,
故答案为:a.
18.如图,在△ABC中,∠ACB=50°,将△ABC绕点C逆时针旋转得到△DEC(点D、E分别与点A、B对应),如果∠ACD与∠ACE的度数之比为3:2,当旋转角大于0°且小于180°时,旋转角的度数为 30°或150° .
【分析】分两种情况:当旋转角小于50°时和当旋转角大于50°时,分别画出图形,由∠ACD与∠ACE的度数之比为3:2,求出∠ACE,即可得到旋转角度数.
解:当旋转角小于50°时,如图:
∵∠ACB=50°,△ABC绕点C逆时针旋转得到△DEC,
∴∠DCE=50°,
∵∠ACD与∠ACE的度数之比为3:2,
∴∠ACE=×50°=20°,
∴旋转角∠BCE=∠ACB﹣∠ACE=30°,
当旋转角大于50°时,如图:
∵∠ACD与∠ACE的度数之比为3:2,∠DCE=∠ACB=50°,
∴∠ACE=2∠DCE=100°,
∴旋转角∠BCE=∠ACB+∠ACE=150°,
故答案为:30°或150°.
三、简答题(本大题共有6题,每题4分,满分24分)
19.计算:(a﹣b)2﹣(2a﹣b)(2a+b).
【分析】根据完全平方公式和平方差公式化简即可.
解:原式=a2﹣2ab+b2﹣(4a2﹣b2)
=a2﹣2ab+b2﹣4a2+b2
=﹣3a2﹣2ab+2b2.
20.计算:()﹣1﹣.
【分析】根据负整数指数幂、分式的除法和减法可以解答本题.
解:()﹣1﹣
=﹣
=﹣
=
=
=
=.
21.因式分解:(x2+4x)2﹣(x2+4x)﹣20.
【分析】直接利用十字相乘法分解因式得出即可.
解:原式=(x2+4x﹣5)(x2+4x+4)
=(x+5)(x﹣1)(x+2)2.
22.因式分解:1﹣a2﹣4b2+4ab.
【分析】先分组,再逆用完全平方公式、平方差公式进行因式分解.
解:1﹣a2﹣4b2+4ab
=1﹣(a2+4b2﹣4ab)
=1﹣(a﹣2b)2
=(1+a﹣2b)[1﹣(a﹣2b)]
=(1+a﹣2b)(1﹣a+2b).
23.已知3m=4,3n=5,分别求3m+n与32m﹣n的值.
【分析】利用同底数幂的乘法的法则,同底数幂的除法的法则,幂的乘方的法则对所求的式子进行整理,再代入运算即可.
解:当3m=4,3n=5时,
3m+n
=3m×3n
=4×5
=20;
32m﹣n
=32m÷3n
=(3m)2÷3n
=42÷5
=16÷5
=.
24.解方程:1+=.
【分析】按照解分式方程的步骤进行计算即可解答.
解:1+=,
1﹣x2+1=x(1﹣x),
解得:x=2,
检验:当x=2时,1﹣x2≠0,
∴x=2是原方程的根.
四、解答题(第25、26每题6分,第27、28每题8分,满分28分)
25.如图,已知四边形ABCD和直线MN.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O成中心对称;
(3)四边形A1B1C1D1与四边形A2B2C2D2的位置关系是 CO .
【分析】(1)根据轴对称的性质即可画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)根据中心对称性质即可画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O成中心对称;
(3)结合以上画图即可得四边形A1B1C1D1与四边形A2B2C2D2的位置关系是.
解:(1)如图,A1B1C1D1即为所求;
(2)如图,A2B2C2D2即为所求;
(3)关于直线CO成轴对称.
故答案为:CO.
26.2022年北京冬奥会开幕在即,参加女子1500米短道速滑的运动员在教练员的指导下努力训练提高竞技水平.在经过指导后,甲运动员的速度是原来的1.1倍,时间缩短了15秒,那么经过指导后,甲运动员的速度是多少?
【分析】设甲运动员原来的速度是x米/秒,则经过指导后的速度是1.1x米/秒,利用时间=路程÷速度,结合经过指导后时间缩短了15秒,即可得出关于x的分式方程,解之经检验后可得出甲运动员原来的速度,再将其代入1.1x中即可求出经过指导后甲运动员的速度.
解:设甲运动员原来的速度是x米/秒,则经过指导后的速度是1.1x米/秒,
依题意得:﹣=15,
解得:x=,
经检验,x=是原方程的解,且符合题意,
∴1.1x=1.1×=10.
答:经过指导后,甲运动员的速度是10米/秒.
27.先化简,再求值:÷(﹣x﹣2),其中x=﹣2.
【分析】原式小括号内的式子进行通分计算,然后再算括号外面的除法,最后代入求值.
解:原式=÷[﹣]
=÷
=
=,
当x=﹣2时,原式===.
28.如图1,长方形纸片ABCD(AD>AB),点O位于边BC上,点E位于边AD上,将纸片沿OE折叠,点C、D的对应点分别为点C′、D′.
(1)当点C′与点A重合时,如图2,如果AD=12,CD=8,联结CE,那么△CDE的周长是 20 ;
(2)如果点F位于边AB上,将纸片沿OF折叠,点B的对应点为点B′.
①当点B′恰好落在线段OC′上时,如图3,那么∠EOF的度数为 90° ;(直接填写答案)
②当∠B′OC′=20°时,作出图形,并写出∠EOF的度数.
【分析】(1)证明DE+EC=AD=12,可得结论;
(2)①利用角平分线的定义以及平角的性质解决问题即可;
②分两种情形,分别画出图形,利用角平分线的定义,平角的性质解决问题即可.
解:(1)如图2中,点C′与点A重合时,
由翻折的性质可知,EA=EC,
∴DE+EC=DE+EA=AD=12,
∴△CDE的周长=DE+EC+CD=12+8=20.
故答案为:20;
(2)①如图3中,
由翻折的性质可知,∠BOF=∠B′OF,∠EOC=∠EOC′,
∵∠BOC=180°,
∴∠EOF=∠EOB′+∠FOB′=(∠COB′+∠BOB′)=∠BOC=90°.
故答案为:90°;
②如图4﹣1中,当OB′值OC′的下方时,
∵∠B′OC′=20°,
∴∠BOB′+∠COC′=180°﹣20°=160°,
∵∠FOB′=∠BOB′,∠EOC′=∠COC′,
∴∠FOB′+∠EOC′=×160°=80°,
∴∠EOF=∠FOB′+∠EOC′+∠B′OC′=100°.
如图4﹣2中,当OB′在OC′的上方时,
∵∠B′OC′=20°,
∴∠BOB′+∠COC′=180°+20°=200°,
∵∠FOB′=∠BOB′,∠EOC′=∠COC′,
∴∠FOB′+∠EOC′=×200°=100°,
∴∠EOF=∠FOB′+∠EOC′﹣∠B′OC′=80°.
综上所述,∠EOF的度数为100°或80°.
同课章节目录
