2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷 (Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷 (Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 264.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 00:00:00 | ||
图片预览

文档简介
人教版九年级数学下册
第二十九章 投影与视图
单元测试训练卷
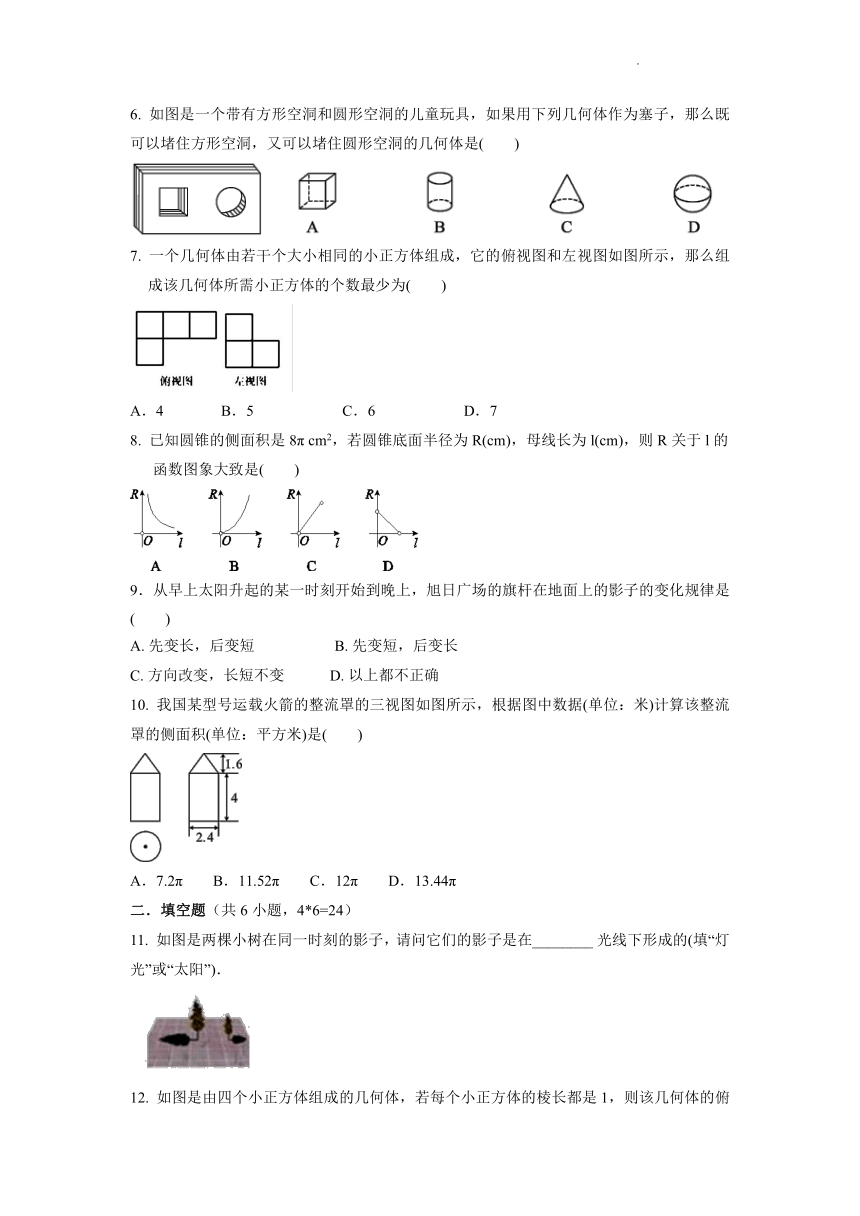
一、选择题(共10小题,4*10=40)
1. 下列结论中正确的有( )
①同一地点、同一时刻,不同物体在阳光照射下,影子的方向是相同的;
②不同物体在任何光线照射下影子的方向都是相同的;
③同一物体在路灯照射下,影子的方向与路灯的位置有关;
④物体在光线照射下,影子的长短仅与物体的长短有关.
A.1个 B.2个 C.3个 D.4个
2. .如图所示的物体的左视图为( )
A B C D
3. 如图所示几何体的左视图是( )
A B C D
4. 6月15日“父亲节”,小明送给父亲一个礼盒(如图所示),该礼盒的主视图是( )
A B C D
5. 某几何体的三视图如图所示,该几何体是( )
A.圆锥 B.圆柱 C.三棱锥 D.球
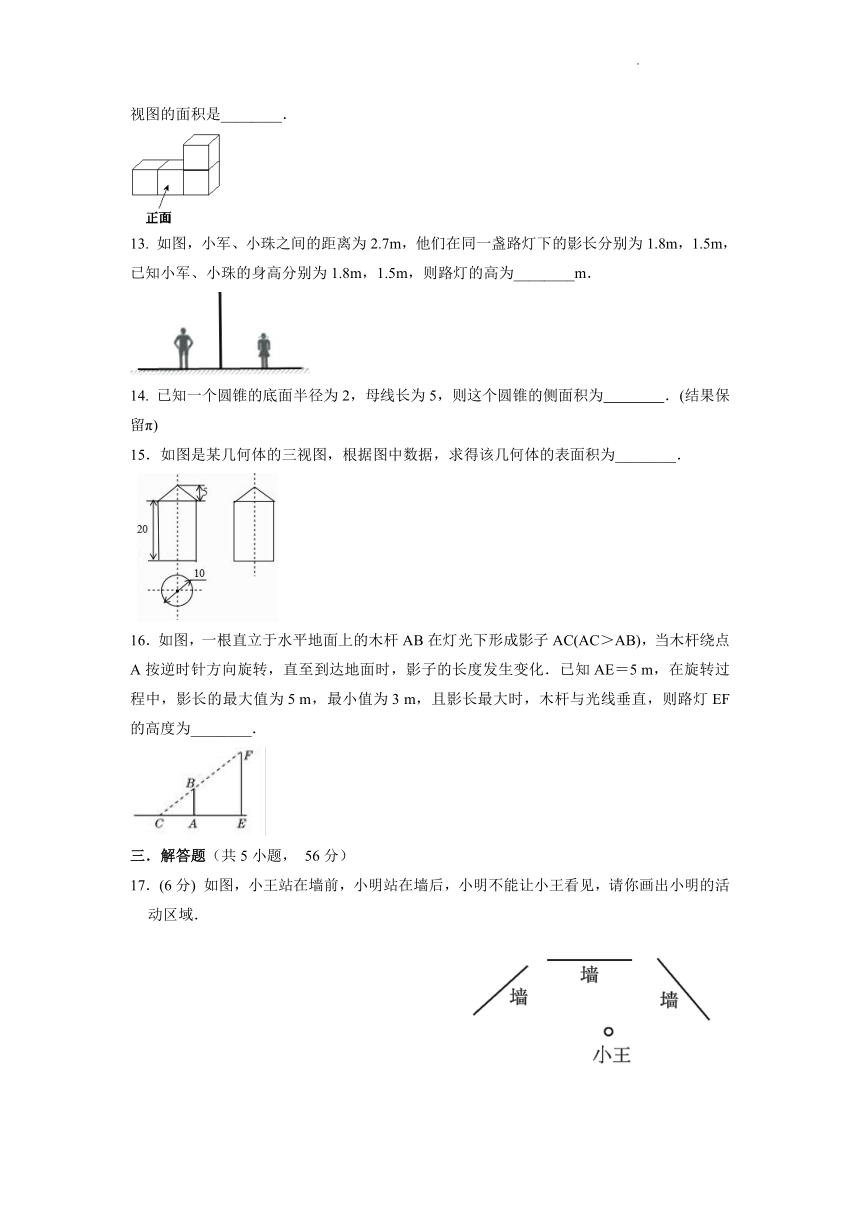
6. 如图是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )
7. 一个几何体由若干个大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为( )
A.4 B.5 C.6 D.7
8. 已知圆锥的侧面积是8π cm2,若圆锥底面半径为R(cm),母线长为l(cm),则R关于l的函数图象大致是( )
9.从早上太阳升起的某一时刻开始到晚上,旭日广场的旗杆在地面上的影子的变化规律是( )
A. 先变长,后变短 B. 先变短,后变长
C. 方向改变,长短不变 D. 以上都不正确
10. 我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:米)计算该整流罩的侧面积(单位:平方米)是( )
A.7.2π B.11.52π C.12π D.13.44π
二.填空题(共6小题,4*6=24)
11. 如图是两棵小树在同一时刻的影子,请问它们的影子是在________ 光线下形成的(填“灯光”或“太阳”).
12. 如图是由四个小正方体组成的几何体,若每个小正方体的棱长都是1,则该几何体的俯视图的面积是________.
13. 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为________m.
14. 已知一个圆锥的底面半径为2,母线长为5,则这个圆锥的侧面积为 .(结果保留π)
15.如图是某几何体的三视图,根据图中数据,求得该几何体的表面积为________.
16.如图,一根直立于水平地面上的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5 m,在旋转过程中,影长的最大值为5 m,最小值为3 m,且影长最大时,木杆与光线垂直,则路灯EF的高度为________.
三.解答题(共5小题, 56分)
17.(6分) 如图,小王站在墙前,小明站在墙后,小明不能让小王看见,请你画出小明的活动区域.
18.(8分) 画出下面图形的三视图:
19.(8分) 如图所示的是某几何体的展开图.
(1)这个几何体的名称是________;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积.(π取3.14)
20.(10分) 有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.
21.(12分) 如图,公路旁有两个高度相等的路灯AB,CD.数学老师杨柳上午去学校时发现高1米的木棒的影子为5米,此时路灯AB在太阳光下的影子恰好落在里程碑E处,他自己的影子恰好落在路灯CD的底部C处.晚自习后回家时,站在上午同一个地方,杨老师发现在路灯CD的灯光下自己的影子恰好落在里程碑E处.
(1)在图中画出杨老师的位置,并画出光线,标明太阳光、灯光;
(2)若杨老师身高为1.8米,他离里程碑E恰4米,求路灯的高.
22.(12分) 某零件厂刚接到要铸造5 000件铁质工件的订单,如图给出了这种工件的三视图.已知铸造这批工件的原料是生铁,待工件铸成后还要在表面涂一层防锈漆,那么完成这批工件需要原料生铁多少吨?涂完这批工件要消耗多少防锈漆?(铁的密度为7.8 g/cm3,1 kg 防锈漆可以涂4 m2的铁器面,三视图单位:cm)
参考答案
1-5BABAA 6-10BBABC
11. 灯光
12. 3
13. 2
14.10π
15. (225+25 )π
16.7.5 m
17.解:如图,小明的活动区域是A,B,C三个阴影部分区域.
18. 解:如图所示:
19. 解:(1)圆柱
(2)如图所示.
(3)V=πR2·h=π×52×20=500π≈1570.
20. (1)解答:如图所示:
(2)由勾股定理得:斜边长为10厘米,S底=×8×6=24 (平方厘米), S侧=(8+6+10)×3=72 (平方厘米), S全=72+24×2=120 (平方厘米).答:这个几何体的全面积是120平方厘米.
21. (1)如图所示,GF表示杨老师的位置.
(2)∵上午去学校时,高1米的木棒的影子为5米,杨老师身高为1.8米,∴杨老师的影长CF为5×1.8=9(米),∵GF⊥AC,DC⊥AC,∴GF∥CD,∴△EGF∽△EDC,∴=,∴=,解得CD=5.85.故路灯高5.85米.
22. 解:∵一件工件的体积为(30×10+10×10)×20=8 000(cm3),∴重量为8 000×7.8=62 400(g)=0.062 4(t),∴铸造5 000 件工件需要原料生铁5 000×0.062 4=312(t).∵一件工件的表面积为2×(30×20+20×20+10×30+10×10)=2 800(cm2)=0.28(m2),∴涂完全部工件要消耗防锈漆 5 000×0.28÷4=350(kg).
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列结论中正确的有( )
①同一地点、同一时刻,不同物体在阳光照射下,影子的方向是相同的;
②不同物体在任何光线照射下影子的方向都是相同的;
③同一物体在路灯照射下,影子的方向与路灯的位置有关;
④物体在光线照射下,影子的长短仅与物体的长短有关.
A.1个 B.2个 C.3个 D.4个
2. .如图所示的物体的左视图为( )
A B C D
3. 如图所示几何体的左视图是( )
A B C D
4. 6月15日“父亲节”,小明送给父亲一个礼盒(如图所示),该礼盒的主视图是( )
A B C D
5. 某几何体的三视图如图所示,该几何体是( )
A.圆锥 B.圆柱 C.三棱锥 D.球
6. 如图是一个带有方形空洞和圆形空洞的儿童玩具,如果用下列几何体作为塞子,那么既可以堵住方形空洞,又可以堵住圆形空洞的几何体是( )
7. 一个几何体由若干个大小相同的小正方体组成,它的俯视图和左视图如图所示,那么组成该几何体所需小正方体的个数最少为( )
A.4 B.5 C.6 D.7
8. 已知圆锥的侧面积是8π cm2,若圆锥底面半径为R(cm),母线长为l(cm),则R关于l的函数图象大致是( )
9.从早上太阳升起的某一时刻开始到晚上,旭日广场的旗杆在地面上的影子的变化规律是( )
A. 先变长,后变短 B. 先变短,后变长
C. 方向改变,长短不变 D. 以上都不正确
10. 我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:米)计算该整流罩的侧面积(单位:平方米)是( )
A.7.2π B.11.52π C.12π D.13.44π
二.填空题(共6小题,4*6=24)
11. 如图是两棵小树在同一时刻的影子,请问它们的影子是在________ 光线下形成的(填“灯光”或“太阳”).
12. 如图是由四个小正方体组成的几何体,若每个小正方体的棱长都是1,则该几何体的俯视图的面积是________.
13. 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为________m.
14. 已知一个圆锥的底面半径为2,母线长为5,则这个圆锥的侧面积为 .(结果保留π)
15.如图是某几何体的三视图,根据图中数据,求得该几何体的表面积为________.
16.如图,一根直立于水平地面上的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5 m,在旋转过程中,影长的最大值为5 m,最小值为3 m,且影长最大时,木杆与光线垂直,则路灯EF的高度为________.
三.解答题(共5小题, 56分)
17.(6分) 如图,小王站在墙前,小明站在墙后,小明不能让小王看见,请你画出小明的活动区域.
18.(8分) 画出下面图形的三视图:
19.(8分) 如图所示的是某几何体的展开图.
(1)这个几何体的名称是________;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积.(π取3.14)
20.(10分) 有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.
21.(12分) 如图,公路旁有两个高度相等的路灯AB,CD.数学老师杨柳上午去学校时发现高1米的木棒的影子为5米,此时路灯AB在太阳光下的影子恰好落在里程碑E处,他自己的影子恰好落在路灯CD的底部C处.晚自习后回家时,站在上午同一个地方,杨老师发现在路灯CD的灯光下自己的影子恰好落在里程碑E处.
(1)在图中画出杨老师的位置,并画出光线,标明太阳光、灯光;
(2)若杨老师身高为1.8米,他离里程碑E恰4米,求路灯的高.
22.(12分) 某零件厂刚接到要铸造5 000件铁质工件的订单,如图给出了这种工件的三视图.已知铸造这批工件的原料是生铁,待工件铸成后还要在表面涂一层防锈漆,那么完成这批工件需要原料生铁多少吨?涂完这批工件要消耗多少防锈漆?(铁的密度为7.8 g/cm3,1 kg 防锈漆可以涂4 m2的铁器面,三视图单位:cm)
参考答案
1-5BABAA 6-10BBABC
11. 灯光
12. 3
13. 2
14.10π
15. (225+25 )π
16.7.5 m
17.解:如图,小明的活动区域是A,B,C三个阴影部分区域.
18. 解:如图所示:
19. 解:(1)圆柱
(2)如图所示.
(3)V=πR2·h=π×52×20=500π≈1570.
20. (1)解答:如图所示:
(2)由勾股定理得:斜边长为10厘米,S底=×8×6=24 (平方厘米), S侧=(8+6+10)×3=72 (平方厘米), S全=72+24×2=120 (平方厘米).答:这个几何体的全面积是120平方厘米.
21. (1)如图所示,GF表示杨老师的位置.
(2)∵上午去学校时,高1米的木棒的影子为5米,杨老师身高为1.8米,∴杨老师的影长CF为5×1.8=9(米),∵GF⊥AC,DC⊥AC,∴GF∥CD,∴△EGF∽△EDC,∴=,∴=,解得CD=5.85.故路灯高5.85米.
22. 解:∵一件工件的体积为(30×10+10×10)×20=8 000(cm3),∴重量为8 000×7.8=62 400(g)=0.062 4(t),∴铸造5 000 件工件需要原料生铁5 000×0.062 4=312(t).∵一件工件的表面积为2×(30×20+20×20+10×30+10×10)=2 800(cm2)=0.28(m2),∴涂完全部工件要消耗防锈漆 5 000×0.28÷4=350(kg).
