北师大版七年级数学下册4.3三角形探索三角形全等的条件(3)教案
文档属性
| 名称 | 北师大版七年级数学下册4.3三角形探索三角形全等的条件(3)教案 |  | |
| 格式 | doc | ||
| 文件大小 | 142.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 09:38:21 | ||
图片预览

文档简介
第四章 三角形
探索三角形全等的条件(3)教学设计
北师大版七年级数学下册
知识与技能:
1、探索三角形全等的条件“边角边” ,并能应用“边角边”来判定两个三角形全等。
2、学习运用逻辑推理,会根据充分的条件作出准确的判定,并严格按照要求格式书写过程。
过程与方法:
1、通过作图对比,培养学生思维的全面性。
2、经历探究三角形全等的条件“边角边”的过程,体会利用动手实验、观察、归纳获得数学结论的过程,培养学生的逻辑思维能力,并会运用数学语言进行简单地推理。
情感、态度与价值观:
(1)通过自主学习和合作探究学习,体验获取数学知识的感受,培养学生勇于创新,多方位解决问题的能力。
(2)体会数学在现实生活中的应用,树立学好数学的信心。
教学重点:掌握三角形全等的条件“边角边” ,并能应用“边角边”来判定两个三角形全等。
教学难点:探索三角形全等的条件“边角边” 及其应用。
教学过程:
一、问题导入:
小淘气闯祸了,不小心打碎了玻璃,打碎成如图的两块,要到玻璃店去照原样配一块,猜想一下带哪一块去?
二、师生互动,深入探究
(一)自主探究:
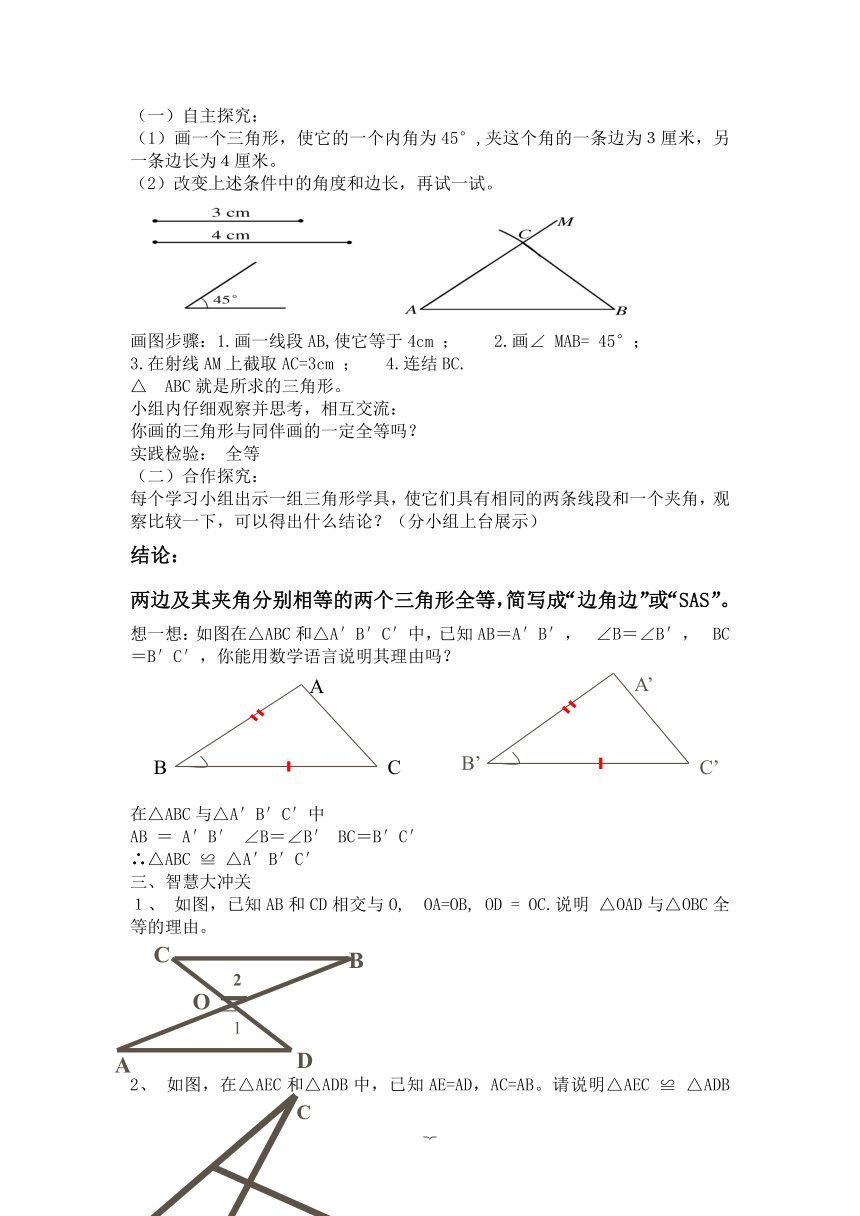
(1)画一个三角形,使它的一个内角为45°,夹这个角的一条边为3厘米,另一条边长为4厘米。
(2)改变上述条件中的角度和边长,再试一试。
画图步骤:1.画一线段AB,使它等于4cm ; 2.画∠ MAB= 45°;
3.在射线AM上截取AC=3cm ; 4.连结BC.
△ ABC就是所求的三角形。
小组内仔细观察并思考,相互交流:
你画的三角形与同伴画的一定全等吗?
实践检验: 全等
(二)合作探究:
每个学习小组出示一组三角形学具,使它们具有相同的两条线段和一个夹角,观察比较一下,可以得出什么结论?(分小组上台展示)
结论:
两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”。
想一想:如图在△ABC和△A′B′C′中,已知AB=A′B′, ∠B=∠B′, BC=B′C′,你能用数学语言说明其理由吗?
在△ABC与△A′B′C′中
AB = A′B′ ∠B=∠B′ BC=B′C′
∴△ABC ≌ △A′B′C′
三、智慧大冲关
1、 如图,已知AB和CD相交与O, OA=OB, OD = OC.说明 △OAD与△OBC全等的理由。
2、 如图,在△AEC和△ADB中,已知AE=AD,AC=AB。请说明△AEC ≌ △ADB的理由。
四、智慧大比拼:
1、已知:如图,AD∥BC,AD=CB.
试说明: △ADC≌△CBA
解:∵AD∥BC ∴∠DAC=∠BCA (两直线平行,内错角相等)
在△ADC和△CBA中
AD=CB
∠1=∠2
AC=CA(公共边)
∴ △ADC≌△CBA(SAS)
2、小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同伴进行交流。
解:在△EDH和△FDH中,
ED=FD ∠EDH=∠FDH DH=DH(公共边)
∴△EDH≌△FDH (SAS) ∴EH=FH(全等三角形对应边相等)
五、学以致用我能行
因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够长的尺子,请你设计一种方案,粗略测出A、B两杆之间的距离。
小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。
解:在△ACB和△DCE中,
AC=DC
∠ACB=∠DCE
BC=EC
∴ △ACB≌△DCE(SAS)
∴ AB=DE (全等三角形对应边相等)
六、畅谈收获我最棒
1.三角形全等的条件,有两边及它们的夹角分别相等的两个三角形全等(边角边或SAS)。
2.用边角边判定三角形全等的注意点:
(1)至少需要三个条件;
(2)必须是两边一夹角(如不是夹角,则不一定全等)
(3)全等的三个条件必须是三角形的对应边和对应角,
如条件不完整,则必须先证明三个条件。
七、作业:
乙组和丙组:第104页:习题4.8 第1、2题
甲组:第104页:习题4.8 第3、4题
教学反思:
①
②
①
②
B’
A
A’
B
C
C’
B
C
A
D
2
1
O
C
A
E
B
D
A
B
C
D
E
F
H
D
PAGE
2
探索三角形全等的条件(3)教学设计
北师大版七年级数学下册
知识与技能:
1、探索三角形全等的条件“边角边” ,并能应用“边角边”来判定两个三角形全等。
2、学习运用逻辑推理,会根据充分的条件作出准确的判定,并严格按照要求格式书写过程。
过程与方法:
1、通过作图对比,培养学生思维的全面性。
2、经历探究三角形全等的条件“边角边”的过程,体会利用动手实验、观察、归纳获得数学结论的过程,培养学生的逻辑思维能力,并会运用数学语言进行简单地推理。
情感、态度与价值观:
(1)通过自主学习和合作探究学习,体验获取数学知识的感受,培养学生勇于创新,多方位解决问题的能力。
(2)体会数学在现实生活中的应用,树立学好数学的信心。
教学重点:掌握三角形全等的条件“边角边” ,并能应用“边角边”来判定两个三角形全等。
教学难点:探索三角形全等的条件“边角边” 及其应用。
教学过程:
一、问题导入:
小淘气闯祸了,不小心打碎了玻璃,打碎成如图的两块,要到玻璃店去照原样配一块,猜想一下带哪一块去?
二、师生互动,深入探究
(一)自主探究:
(1)画一个三角形,使它的一个内角为45°,夹这个角的一条边为3厘米,另一条边长为4厘米。
(2)改变上述条件中的角度和边长,再试一试。
画图步骤:1.画一线段AB,使它等于4cm ; 2.画∠ MAB= 45°;
3.在射线AM上截取AC=3cm ; 4.连结BC.
△ ABC就是所求的三角形。
小组内仔细观察并思考,相互交流:
你画的三角形与同伴画的一定全等吗?
实践检验: 全等
(二)合作探究:
每个学习小组出示一组三角形学具,使它们具有相同的两条线段和一个夹角,观察比较一下,可以得出什么结论?(分小组上台展示)
结论:
两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”。
想一想:如图在△ABC和△A′B′C′中,已知AB=A′B′, ∠B=∠B′, BC=B′C′,你能用数学语言说明其理由吗?
在△ABC与△A′B′C′中
AB = A′B′ ∠B=∠B′ BC=B′C′
∴△ABC ≌ △A′B′C′
三、智慧大冲关
1、 如图,已知AB和CD相交与O, OA=OB, OD = OC.说明 △OAD与△OBC全等的理由。
2、 如图,在△AEC和△ADB中,已知AE=AD,AC=AB。请说明△AEC ≌ △ADB的理由。
四、智慧大比拼:
1、已知:如图,AD∥BC,AD=CB.
试说明: △ADC≌△CBA
解:∵AD∥BC ∴∠DAC=∠BCA (两直线平行,内错角相等)
在△ADC和△CBA中
AD=CB
∠1=∠2
AC=CA(公共边)
∴ △ADC≌△CBA(SAS)
2、小兰做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同伴进行交流。
解:在△EDH和△FDH中,
ED=FD ∠EDH=∠FDH DH=DH(公共边)
∴△EDH≌△FDH (SAS) ∴EH=FH(全等三角形对应边相等)
五、学以致用我能行
因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够长的尺子,请你设计一种方案,粗略测出A、B两杆之间的距离。
小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。
解:在△ACB和△DCE中,
AC=DC
∠ACB=∠DCE
BC=EC
∴ △ACB≌△DCE(SAS)
∴ AB=DE (全等三角形对应边相等)
六、畅谈收获我最棒
1.三角形全等的条件,有两边及它们的夹角分别相等的两个三角形全等(边角边或SAS)。
2.用边角边判定三角形全等的注意点:
(1)至少需要三个条件;
(2)必须是两边一夹角(如不是夹角,则不一定全等)
(3)全等的三个条件必须是三角形的对应边和对应角,
如条件不完整,则必须先证明三个条件。
七、作业:
乙组和丙组:第104页:习题4.8 第1、2题
甲组:第104页:习题4.8 第3、4题
教学反思:
①
②
①
②
B’
A
A’
B
C
C’
B
C
A
D
2
1
O
C
A
E
B
D
A
B
C
D
E
F
H
D
PAGE
2
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
