人教版四年级数学下册 1.1加、减法的意义和各部分间的关系 课件(共19张PPT)
文档属性
| 名称 | 人教版四年级数学下册 1.1加、减法的意义和各部分间的关系 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
1.1加、减法的意义和各部分间的关系
教学目标
1.概括出减法的意义,对减法的认识从感性上升到理性。
2.理解并掌握加减法之间的关系。
猴妈妈给小猴子买了3个桃子,但它吃完了3个还想吃,于是猴子妈妈又买了2个。
1.小猴子一共吃了多少个桃子?
2.第一次比第二次多吃了几个桃子?
复习导入
思考?
一列高铁从西宁开往拉萨。西宁至格尔木的铁路长
814km,格尔木至拉萨的铁路长1142km。西宁至拉萨的铁路
长多少km?
情境引入
问题:1. 已知西宁至格尔木的路程以及格尔木至拉萨的路程,求西宁至拉萨的路程。
2.题中的数量关系用线段图表示。
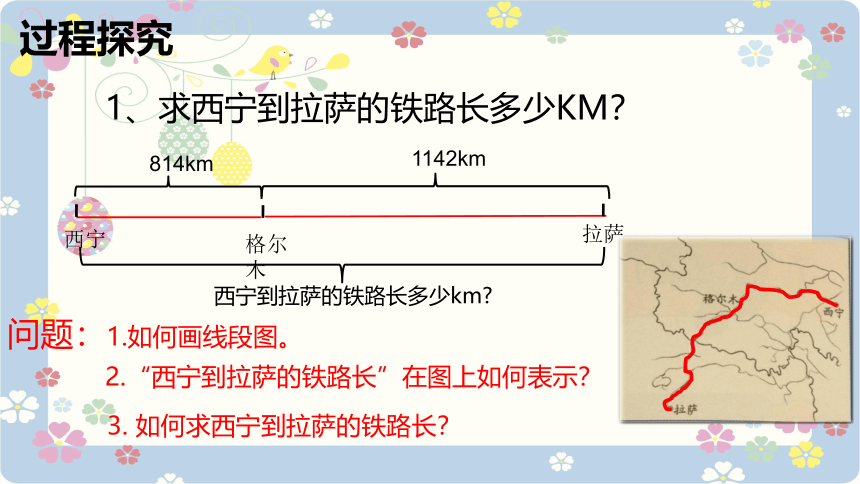
问题:1.如何画线段图。
3. 如何求西宁到拉萨的铁路长?
2.“西宁到拉萨的铁路长”在图上如何表示?
西宁到拉萨的铁路长多少km
西宁
拉萨
格尔木
814km
1142km
1、求西宁到拉萨的铁路长多少KM?
过程探究
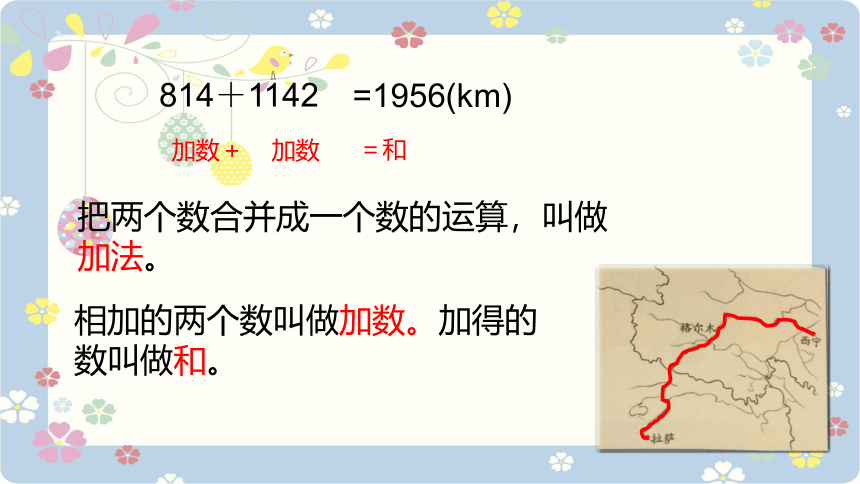
把两个数合并成一个数的运算,叫做加法。
相加的两个数叫做加数。加得的数叫做和。
814+1142
加数+
加数
=1956(km)
=和
2、如图所示,求格尔木至拉萨的铁路长?
西宁到拉萨的铁路长1956km
西宁
拉萨
格尔木
814km
km
1956-814=1142(千米)
=
西宁到拉萨的铁路长1956km
西宁
拉萨
格尔木
km
1142km
1956-1142=814(千米)
3、如图所示,求西宁到格尔木的铁路长多少千米?
1956-814=1142
1956-1142=814
被减数
减数
差
-
=
什么是减法?
已知两个数的和与其中的一个加数,求另一个加数的运算,叫做减法。在减法中,已知的和叫做被减数。
814+1142=1956
加数+加数=和
过程探究
1.加法各部分间的关系。
和=加数+加数
问题:已知和与一个加数,能求出另一个加数吗?
加数=和-另一个加数
讨论分析
2.减法各部分间的关系。
差=
问题:已知被减数和差,能求出减数吗?
减数=被减数-差
问题:已知减数和差,能求出被减数吗?
被减数=减数+差
被减数-减数
问题:加法与减法间有什么关系?
减法是加法的逆运算。
差=被减数-减数
减数=被减数-差
被减数=减数+差
和=加数+加数
加数=和-另一个加数
3.加法与减法间的关系。
经典例题
一道减法算式中,被减数、减数和差存在下面的关系,请写出这道减法算式。
被减数+减数+差=660
减数–差=70
被减数 + 减数 + 差 = 660
减数 – 差 = 70
330
减数:
差:
330
70
=
330-70=260
差:260÷2=130
330
被减数:660÷2=330
130
减数:130+70=200
减法算式:330-200=130
2900-500=
2900-2400=
500
1. 根据2400+500=2900,写出下面的得数。
2400
巩固新知
30+19=49
203+147=350
49-19=30
49-30=19
67-50=17
850-239=611
2. 根据加、减法各部分间的关系,写出另外两个等式。
350-147=203
350-203=147
50+17=67
67-17=50
239+611=850
850-611=239
3.填写下表
(1)
(2)
49
58
326
292
541
16
课堂小结
加法减法的意义:
把两个数合并成一个数的运算,叫做加法。
已知两个数的和与其中的一个加数,求另一个加数的运算,叫做减法。
减法是加法的逆运算。
加法与减法间的关系:
1.1加、减法的意义和各部分间的关系
教学目标
1.概括出减法的意义,对减法的认识从感性上升到理性。
2.理解并掌握加减法之间的关系。
猴妈妈给小猴子买了3个桃子,但它吃完了3个还想吃,于是猴子妈妈又买了2个。
1.小猴子一共吃了多少个桃子?
2.第一次比第二次多吃了几个桃子?
复习导入
思考?
一列高铁从西宁开往拉萨。西宁至格尔木的铁路长
814km,格尔木至拉萨的铁路长1142km。西宁至拉萨的铁路
长多少km?
情境引入
问题:1. 已知西宁至格尔木的路程以及格尔木至拉萨的路程,求西宁至拉萨的路程。
2.题中的数量关系用线段图表示。
问题:1.如何画线段图。
3. 如何求西宁到拉萨的铁路长?
2.“西宁到拉萨的铁路长”在图上如何表示?
西宁到拉萨的铁路长多少km
西宁
拉萨
格尔木
814km
1142km
1、求西宁到拉萨的铁路长多少KM?
过程探究
把两个数合并成一个数的运算,叫做加法。
相加的两个数叫做加数。加得的数叫做和。
814+1142
加数+
加数
=1956(km)
=和
2、如图所示,求格尔木至拉萨的铁路长?
西宁到拉萨的铁路长1956km
西宁
拉萨
格尔木
814km
km
1956-814=1142(千米)
=
西宁到拉萨的铁路长1956km
西宁
拉萨
格尔木
km
1142km
1956-1142=814(千米)
3、如图所示,求西宁到格尔木的铁路长多少千米?
1956-814=1142
1956-1142=814
被减数
减数
差
-
=
什么是减法?
已知两个数的和与其中的一个加数,求另一个加数的运算,叫做减法。在减法中,已知的和叫做被减数。
814+1142=1956
加数+加数=和
过程探究
1.加法各部分间的关系。
和=加数+加数
问题:已知和与一个加数,能求出另一个加数吗?
加数=和-另一个加数
讨论分析
2.减法各部分间的关系。
差=
问题:已知被减数和差,能求出减数吗?
减数=被减数-差
问题:已知减数和差,能求出被减数吗?
被减数=减数+差
被减数-减数
问题:加法与减法间有什么关系?
减法是加法的逆运算。
差=被减数-减数
减数=被减数-差
被减数=减数+差
和=加数+加数
加数=和-另一个加数
3.加法与减法间的关系。
经典例题
一道减法算式中,被减数、减数和差存在下面的关系,请写出这道减法算式。
被减数+减数+差=660
减数–差=70
被减数 + 减数 + 差 = 660
减数 – 差 = 70
330
减数:
差:
330
70
=
330-70=260
差:260÷2=130
330
被减数:660÷2=330
130
减数:130+70=200
减法算式:330-200=130
2900-500=
2900-2400=
500
1. 根据2400+500=2900,写出下面的得数。
2400
巩固新知
30+19=49
203+147=350
49-19=30
49-30=19
67-50=17
850-239=611
2. 根据加、减法各部分间的关系,写出另外两个等式。
350-147=203
350-203=147
50+17=67
67-17=50
239+611=850
850-611=239
3.填写下表
(1)
(2)
49
58
326
292
541
16
课堂小结
加法减法的意义:
把两个数合并成一个数的运算,叫做加法。
已知两个数的和与其中的一个加数,求另一个加数的运算,叫做减法。
减法是加法的逆运算。
加法与减法间的关系:
