2021-2022学年华东师大版九年级数学下册第28章样本与总单元复习训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学下册第28章样本与总单元复习训练卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 180.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 00:00:00 | ||
图片预览



文档简介
华东师大版九年级数学下册
第28章 样本与总体
单元复习训练卷
一、选择题(共10小题,4*10=40)
1. 下列四种调查:①调查某班学生的身高情况;②调查某城市的空气质量;③调查某风景区全年的游客流量;④调查某批汽车的抗撞击能力.其中适合用全面调查方式的是( )
A.① B.② C.③ D.④
2. 为了考察一批电视机的使用寿命,从中任意抽取了10台进行实验,在这个问题中,样本是( )
A.抽取的10台电视机
B.这一批电视机的使用寿命
C.任意10台电视机
D.抽取的10台电视机的使用寿命
3. 为了了解某市九年级学生学业水平考试的数学成绩,从中随机抽取了1 000名学生的数学成绩,下列说法正确的是( )
A.该市九年级学生是总体
B.每一名九年级学生是个体
C.1 000名九年级学生是总体的一个样本
D.样本容量是1 000
4. 为估计鱼塘中的鱼的数量,可以先从鱼塘中随机打捞50条鱼,在每条鱼身上做上记号后,把这些鱼放归鱼塘,经过一段时间,等这些鱼完全混合于鱼群后,再从鱼塘中随机打捞50条鱼,发现只有2条鱼是前面做好记号的,那么可以估计这个鱼塘鱼的数量约为( )
A.1 250条 B.1 750条
C.2 500条 D.5 000条
5. 中学生骑电动车上学给交通安全带来了隐患.为了解某中学2 500位学生家长对“中学生骑电动车上学”的态度,从中随机调查了400位家长,结果有360位家长持反对态度,则下列说法正确的是( )
A.调查方式是普查 B.该校只有360位家长持反对态度
C.样本是360位家长 D.该校约有90%的家长持反对态度
6. 七年级(1)班与(2)班各选出20名学生进行英文打字比赛,通过对参赛学生每分钟输入的单词个数进行统计,两班成绩的平均数相同,(1)班成绩的方差为17.5,(2)班成绩的方差为15.由此可知( )
A.(1)班比(2)班成绩稳定 B.(2)班比(1)班成绩稳定
C.两班的成绩一样稳定 D.无法确定哪个班的成绩更稳定
7. 某家庭搬进新居后又添置了新的电冰箱、电热水器等家用电器,为了了解用电量的大小,该家庭在6月份初连续几天观察电表的度数,电表显示的度数如下表:
日期 1日 2日 3日 4日 5日 6日 7日 8日
电表显示度数(度) 115 118 122 127 133 136 140 143
估计这个家庭六月份用电度数为( )
A.105度 B.108.5度
C.120度 D.124度
8. 为了从甲、乙、丙、丁四位同学中选派两位选手参加数学竞赛,老师对他们的五次数学测验成绩进行统计,得出他们的平均分数均为85分,且s甲2=100,s乙2=110,s丙2=120,s丁2=90.根据统计结果,派去参加竞赛的两位同学是( )
A.甲、乙 B.甲、丙
C.甲、丁 D.乙、丙
9.如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
A. 5~10元 B10~15元
C.15~20元 D. 20~25元
10. 某校为了了解学生课外阅读情况,随机调查了50名学生平均每天的课外阅读时间,并绘制成条形图,如图所示,据此可以估计出该校所有学生平均每人每天的课外阅读时间为( )
A.1.5小时 B.1.0小时
C.0.6小时 D.0.5小时
二.填空题(共6小题,4*6=24)
11. 为了了解全校学生的视力情况,小明、小华、小李三个同学分别设计了三个方案.
①小明:检查全班每个同学的视力,以此推算出全校学生的视力情况.
②小华:在校医室找到2016年全校的体检表,由此了解全校学生视力情况.
③小李:抽取全校学号为5的倍数的同学,检查视力,从而估计全校学生视力的情况.
以上的调查方案最合适的是____.(填写序号)
12. 某校要了解七年级新生的身高情况,在七年级四个班中,每班抽10名学生进行检测,在这个问题中,总体是______________________,样本是______________________________,样本容量是________.
13. 中央电视台《焦点访谈》播出了《泡出来的“毒凤爪”》后,各级工商、施法部门高度重视食品安全,他们欲查市场上某种食品的色素含量是否符合国家标准,这种调查适合用 .(填入普查或者抽样调查)
14. 为了了解全校学生的视力情况,小明、小华、小李三个同学分别设计了三个方案.
①小明:检查全班每个同学的视力,以此推算出全校学生的视力情况.
②小华:在校医室找到2000年全校的体检表,由此了解全校学生视力情况.
③小李:抽取全校学号为5的倍数的同学,检查视力,从而估计全校学生视力情况.
以上的调查方案最合适的是 (填写序号).
15.为了估算湖里有多少条鱼,从湖里捕上50条做标记,然后放回湖里,经过一段时间待标记的鱼全混合于鱼群中后,第二次捕得100条,发现其中带标记的鱼有2条,据此可以估算湖里有鱼______条.
16.一组数据共有50个,分成四组后其中前三组的频率分别是0.25、0.15、0.3,则第四组的数据频数为__ __.
三.解答题(共5小题, 56分)
17.(6分) 下列调查适合普查还是抽样调查?填在括号里.
(1)了解你所在班级的每个学生穿几号鞋;
(2)了解节能灯的使用寿命;
(3)了解我市八年级学生的视力情况;
(4)了解实验田里水稻的穗长.
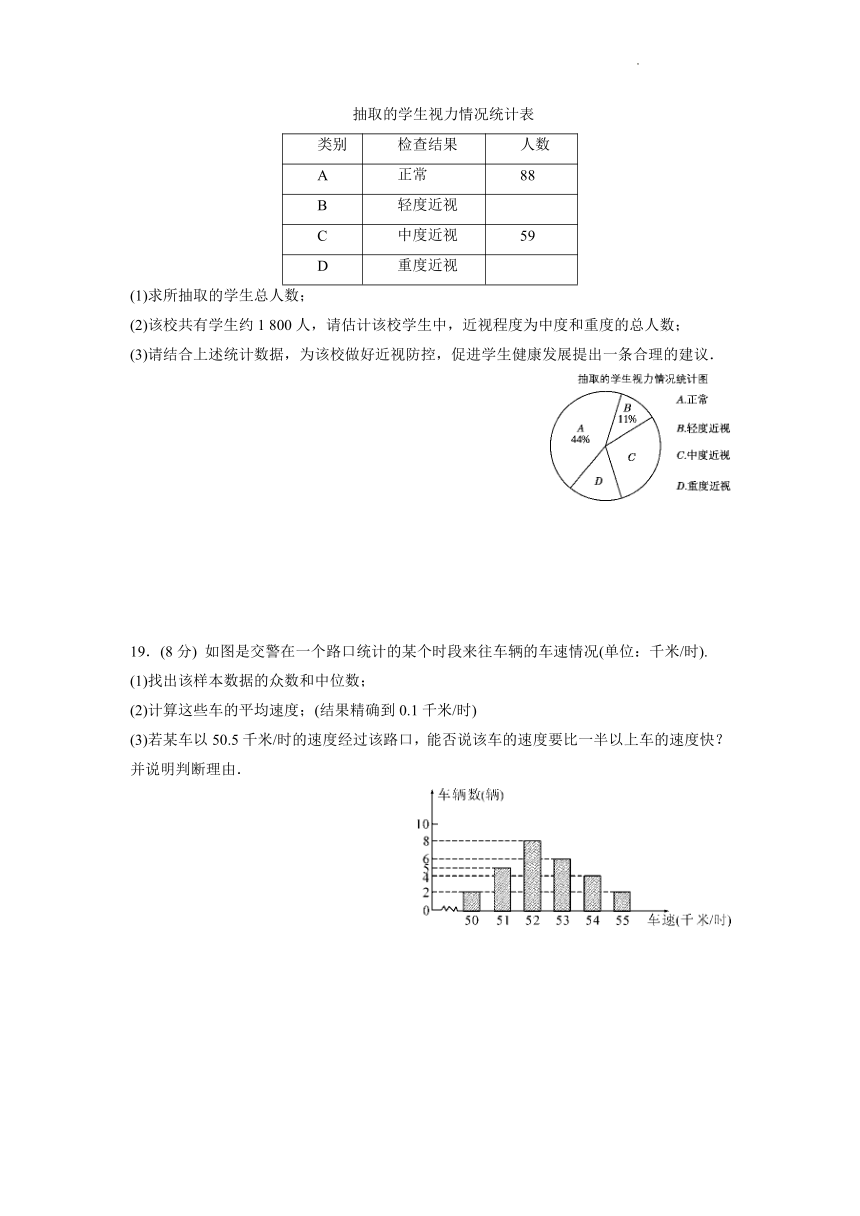
18.(8分) 在创建“浙江省健康促进学校”的过程中,某数学兴趣小组针对视力情况随机抽取本校部分学生进行调查,并按照国家分类标准统计人数,绘制成如下两幅不完整的统计图表,请根据图表信息解答下列问题:
抽取的学生视力情况统计表
类别 检查结果 人数
A 正常 88
B 轻度近视
C 中度近视 59
D 重度近视
(1)求所抽取的学生总人数;
(2)该校共有学生约1 800人,请估计该校学生中,近视程度为中度和重度的总人数;
(3)请结合上述统计数据,为该校做好近视防控,促进学生健康发展提出一条合理的建议.
19.(8分) 如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时).
(1)找出该样本数据的众数和中位数;
(2)计算这些车的平均速度;(结果精确到0.1千米/时)
(3)若某车以50.5千米/时的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.
20.(10分) “低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了单位员工上下班的交通方式,绘制了如下统计图:
(1)填空:样本中的总人数为____;开私家车的人数m=____;扇形统计图中“骑自行车”所在扇形的圆心角为____度;
(2)补全条形统计图;
(3)该单位共有2000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行、坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
21.(12分) 某校部分男生分3组进行引体向上训练,对训练前后的成绩进行相关数据整理的统计图如下.
(1)求训练后第一组平均成绩比训练前增长的百分数;
(2)小明在分析的图表后,声称他发现了一个错误:“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%,所以第二组的平均成绩不可能提高3个这么多”,你同意小明的观点吗?请说明理由;
(3)你认为哪一组的训练效果最好?请说明理由.
22.(12分) 某中学为了预测本校应届毕业生“一分钟跳绳”项目的考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图1的部分频数分布直方图(从左到右依次为六个小组,每小组含最小值,不含最大值)和图2扇形统计图.根据统计图提供的信息解答下列问题:
(1)补全图1频数分布直方图,并指出这个样本数据的中位数落在第 小组;
(2)若“一分钟跳绳”不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩的优秀人数;
(3)若“一分钟跳绳”成绩不低于170次的为满分,不低于130次的为优秀,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?
参考答案
1-5ADDAD 6-10BCCCB
11.③ 12. 七年级新生的身高情况,所抽出的40名新生的身高情况,40 13. 抽样调查
14.③ 15. 2500 16.15
17. (1)普查 (2)抽样调查 (3)抽样调查 (4)抽样调查
18.解:(1)88÷44%=200(人).∴所抽取的学生总人数为200人.
(2)1 800×(1-44%-11%)=810(人).∴估计该校学生中,近视程度为中度和重度的总人数是810人.
(3)该校学生近视程度为中度和重度的人数所占百分比为45%,说明该校学生近视程度较为严重,建议学校加强电子产品进校园及使用的管控(建议不唯一).
19.解:(1)该样本数据的众数为52,中位数为52
(2)≈52.4(千米/时)
(3)不能.理由如下:由(1)知该样本的中位数为52,所以可以估计该路段的车辆大约有一半车的速度要快于52千米/时,该车的速度是50.5千米/时,小于52千米/时,所以不能说该车的速度要比一半以上车的速度快
20.解:(1)80 20 72
(2)骑自行车的人数为:80×20%=16(人),补图略
(3)设原来开私家车的人中有x人改为骑自行车,由题意得,2000×25%-x≤2000×20%+x,解得x≥50,即原来开私家车的人中至少有50人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数
21.解:(1)约67%.
(2)不同意小明的观点,∵第二组的平均成绩增加,8×10%+6×20%+5×20%+0×50%=3(个).
(3)本题答案不唯一,下列解法供参考:认为第一组的训练效果最好,因为训练后第一组的平均成绩比训练前增长的百分数最大.
22.解:(1)总人数是:10÷20%=50(人),第四组的人数是:50﹣4﹣10﹣16﹣6﹣4=10,中位数位于第三组,补全图1如下;
,
(2)该校九年级女生“一分钟跳绳”成绩为优秀的人数是:×260=104(人);
(3)成绩是优秀的人数是:10+6+4=20(人),成绩为满分的人数是4,则从成绩为优秀的女生中任选一人,她的成绩为满分的概率是=0.2.
第28章 样本与总体
单元复习训练卷
一、选择题(共10小题,4*10=40)
1. 下列四种调查:①调查某班学生的身高情况;②调查某城市的空气质量;③调查某风景区全年的游客流量;④调查某批汽车的抗撞击能力.其中适合用全面调查方式的是( )
A.① B.② C.③ D.④
2. 为了考察一批电视机的使用寿命,从中任意抽取了10台进行实验,在这个问题中,样本是( )
A.抽取的10台电视机
B.这一批电视机的使用寿命
C.任意10台电视机
D.抽取的10台电视机的使用寿命
3. 为了了解某市九年级学生学业水平考试的数学成绩,从中随机抽取了1 000名学生的数学成绩,下列说法正确的是( )
A.该市九年级学生是总体
B.每一名九年级学生是个体
C.1 000名九年级学生是总体的一个样本
D.样本容量是1 000
4. 为估计鱼塘中的鱼的数量,可以先从鱼塘中随机打捞50条鱼,在每条鱼身上做上记号后,把这些鱼放归鱼塘,经过一段时间,等这些鱼完全混合于鱼群后,再从鱼塘中随机打捞50条鱼,发现只有2条鱼是前面做好记号的,那么可以估计这个鱼塘鱼的数量约为( )
A.1 250条 B.1 750条
C.2 500条 D.5 000条
5. 中学生骑电动车上学给交通安全带来了隐患.为了解某中学2 500位学生家长对“中学生骑电动车上学”的态度,从中随机调查了400位家长,结果有360位家长持反对态度,则下列说法正确的是( )
A.调查方式是普查 B.该校只有360位家长持反对态度
C.样本是360位家长 D.该校约有90%的家长持反对态度
6. 七年级(1)班与(2)班各选出20名学生进行英文打字比赛,通过对参赛学生每分钟输入的单词个数进行统计,两班成绩的平均数相同,(1)班成绩的方差为17.5,(2)班成绩的方差为15.由此可知( )
A.(1)班比(2)班成绩稳定 B.(2)班比(1)班成绩稳定
C.两班的成绩一样稳定 D.无法确定哪个班的成绩更稳定
7. 某家庭搬进新居后又添置了新的电冰箱、电热水器等家用电器,为了了解用电量的大小,该家庭在6月份初连续几天观察电表的度数,电表显示的度数如下表:
日期 1日 2日 3日 4日 5日 6日 7日 8日
电表显示度数(度) 115 118 122 127 133 136 140 143
估计这个家庭六月份用电度数为( )
A.105度 B.108.5度
C.120度 D.124度
8. 为了从甲、乙、丙、丁四位同学中选派两位选手参加数学竞赛,老师对他们的五次数学测验成绩进行统计,得出他们的平均分数均为85分,且s甲2=100,s乙2=110,s丙2=120,s丁2=90.根据统计结果,派去参加竞赛的两位同学是( )
A.甲、乙 B.甲、丙
C.甲、丁 D.乙、丙
9.如图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
A. 5~10元 B10~15元
C.15~20元 D. 20~25元
10. 某校为了了解学生课外阅读情况,随机调查了50名学生平均每天的课外阅读时间,并绘制成条形图,如图所示,据此可以估计出该校所有学生平均每人每天的课外阅读时间为( )
A.1.5小时 B.1.0小时
C.0.6小时 D.0.5小时
二.填空题(共6小题,4*6=24)
11. 为了了解全校学生的视力情况,小明、小华、小李三个同学分别设计了三个方案.
①小明:检查全班每个同学的视力,以此推算出全校学生的视力情况.
②小华:在校医室找到2016年全校的体检表,由此了解全校学生视力情况.
③小李:抽取全校学号为5的倍数的同学,检查视力,从而估计全校学生视力的情况.
以上的调查方案最合适的是____.(填写序号)
12. 某校要了解七年级新生的身高情况,在七年级四个班中,每班抽10名学生进行检测,在这个问题中,总体是______________________,样本是______________________________,样本容量是________.
13. 中央电视台《焦点访谈》播出了《泡出来的“毒凤爪”》后,各级工商、施法部门高度重视食品安全,他们欲查市场上某种食品的色素含量是否符合国家标准,这种调查适合用 .(填入普查或者抽样调查)
14. 为了了解全校学生的视力情况,小明、小华、小李三个同学分别设计了三个方案.
①小明:检查全班每个同学的视力,以此推算出全校学生的视力情况.
②小华:在校医室找到2000年全校的体检表,由此了解全校学生视力情况.
③小李:抽取全校学号为5的倍数的同学,检查视力,从而估计全校学生视力情况.
以上的调查方案最合适的是 (填写序号).
15.为了估算湖里有多少条鱼,从湖里捕上50条做标记,然后放回湖里,经过一段时间待标记的鱼全混合于鱼群中后,第二次捕得100条,发现其中带标记的鱼有2条,据此可以估算湖里有鱼______条.
16.一组数据共有50个,分成四组后其中前三组的频率分别是0.25、0.15、0.3,则第四组的数据频数为__ __.
三.解答题(共5小题, 56分)
17.(6分) 下列调查适合普查还是抽样调查?填在括号里.
(1)了解你所在班级的每个学生穿几号鞋;
(2)了解节能灯的使用寿命;
(3)了解我市八年级学生的视力情况;
(4)了解实验田里水稻的穗长.
18.(8分) 在创建“浙江省健康促进学校”的过程中,某数学兴趣小组针对视力情况随机抽取本校部分学生进行调查,并按照国家分类标准统计人数,绘制成如下两幅不完整的统计图表,请根据图表信息解答下列问题:
抽取的学生视力情况统计表
类别 检查结果 人数
A 正常 88
B 轻度近视
C 中度近视 59
D 重度近视
(1)求所抽取的学生总人数;
(2)该校共有学生约1 800人,请估计该校学生中,近视程度为中度和重度的总人数;
(3)请结合上述统计数据,为该校做好近视防控,促进学生健康发展提出一条合理的建议.
19.(8分) 如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时).
(1)找出该样本数据的众数和中位数;
(2)计算这些车的平均速度;(结果精确到0.1千米/时)
(3)若某车以50.5千米/时的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.
20.(10分) “低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了单位员工上下班的交通方式,绘制了如下统计图:
(1)填空:样本中的总人数为____;开私家车的人数m=____;扇形统计图中“骑自行车”所在扇形的圆心角为____度;
(2)补全条形统计图;
(3)该单位共有2000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行、坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
21.(12分) 某校部分男生分3组进行引体向上训练,对训练前后的成绩进行相关数据整理的统计图如下.
(1)求训练后第一组平均成绩比训练前增长的百分数;
(2)小明在分析的图表后,声称他发现了一个错误:“训练后第二组男生引体向上个数没有变化的人数占该组人数的50%,所以第二组的平均成绩不可能提高3个这么多”,你同意小明的观点吗?请说明理由;
(3)你认为哪一组的训练效果最好?请说明理由.
22.(12分) 某中学为了预测本校应届毕业生“一分钟跳绳”项目的考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图1的部分频数分布直方图(从左到右依次为六个小组,每小组含最小值,不含最大值)和图2扇形统计图.根据统计图提供的信息解答下列问题:
(1)补全图1频数分布直方图,并指出这个样本数据的中位数落在第 小组;
(2)若“一分钟跳绳”不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩的优秀人数;
(3)若“一分钟跳绳”成绩不低于170次的为满分,不低于130次的为优秀,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?
参考答案
1-5ADDAD 6-10BCCCB
11.③ 12. 七年级新生的身高情况,所抽出的40名新生的身高情况,40 13. 抽样调查
14.③ 15. 2500 16.15
17. (1)普查 (2)抽样调查 (3)抽样调查 (4)抽样调查
18.解:(1)88÷44%=200(人).∴所抽取的学生总人数为200人.
(2)1 800×(1-44%-11%)=810(人).∴估计该校学生中,近视程度为中度和重度的总人数是810人.
(3)该校学生近视程度为中度和重度的人数所占百分比为45%,说明该校学生近视程度较为严重,建议学校加强电子产品进校园及使用的管控(建议不唯一).
19.解:(1)该样本数据的众数为52,中位数为52
(2)≈52.4(千米/时)
(3)不能.理由如下:由(1)知该样本的中位数为52,所以可以估计该路段的车辆大约有一半车的速度要快于52千米/时,该车的速度是50.5千米/时,小于52千米/时,所以不能说该车的速度要比一半以上车的速度快
20.解:(1)80 20 72
(2)骑自行车的人数为:80×20%=16(人),补图略
(3)设原来开私家车的人中有x人改为骑自行车,由题意得,2000×25%-x≤2000×20%+x,解得x≥50,即原来开私家车的人中至少有50人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数
21.解:(1)约67%.
(2)不同意小明的观点,∵第二组的平均成绩增加,8×10%+6×20%+5×20%+0×50%=3(个).
(3)本题答案不唯一,下列解法供参考:认为第一组的训练效果最好,因为训练后第一组的平均成绩比训练前增长的百分数最大.
22.解:(1)总人数是:10÷20%=50(人),第四组的人数是:50﹣4﹣10﹣16﹣6﹣4=10,中位数位于第三组,补全图1如下;
,
(2)该校九年级女生“一分钟跳绳”成绩为优秀的人数是:×260=104(人);
(3)成绩是优秀的人数是:10+6+4=20(人),成绩为满分的人数是4,则从成绩为优秀的女生中任选一人,她的成绩为满分的概率是=0.2.
