2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试训练卷(Word版含答案) | 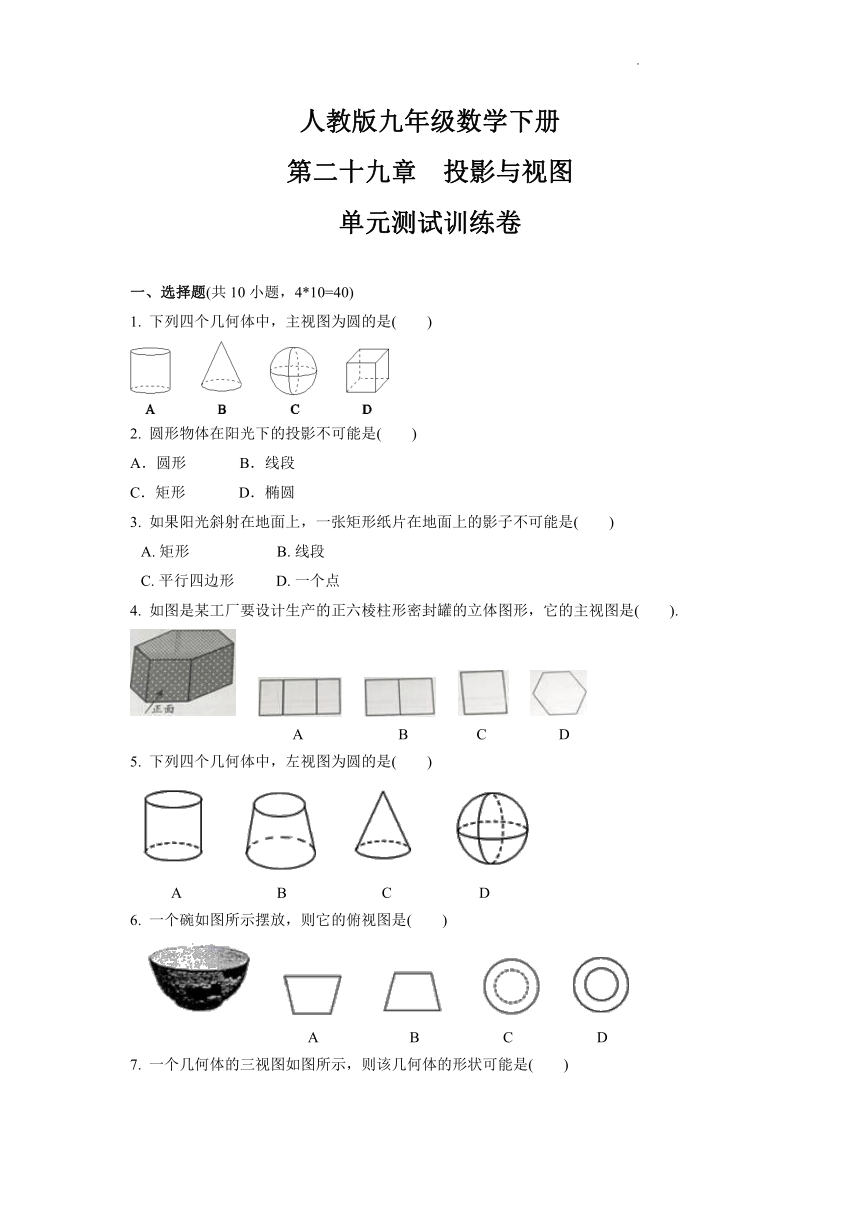 | |
| 格式 | docx | ||
| 文件大小 | 293.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 20:55:20 | ||
图片预览




文档简介
人教版九年级数学下册
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列四个几何体中,主视图为圆的是( )
2. 圆形物体在阳光下的投影不可能是( )
A.圆形 B.线段
C.矩形 D.椭圆
3. 如果阳光斜射在地面上,一张矩形纸片在地面上的影子不可能是( )
A. 矩形 B. 线段
C. 平行四边形 D. 一个点
4. 如图是某工厂要设计生产的正六棱柱形密封罐的立体图形,它的主视图是( ).
A B C D
5. 下列四个几何体中,左视图为圆的是( )
A B C D
6. 一个碗如图所示摆放,则它的俯视图是( )
A B C D
7. 一个几何体的三视图如图所示,则该几何体的形状可能是( )
A B C D
8. 学校小卖部货架上摆放着若干盒某品牌方便面,它们的三视图如图所示,则货架上的方便面至少有( )
A.7盒 B.8盒 C.9盒 D.10盒
9.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小正方体的个数,则以下说法正确的是( )
A.x=1或2,y=3 B.x=1或2,y=1或3
C.x=1,y=1或3 D.x=2,y=1或3
10. 某数学课外活动小组想利用树影测量树高,他们在同一时刻测得一身高为1.5 m的同学的影长为1.35 m,由于大树靠近一幢建筑物,因此树影的一部分落在建筑物上,如图,他们测得地面部分的影长为3.6 m,建筑物上的影长为1.8 m,则树的高度为( )
A.5.4 m B.5.8 m C.5.22 m D.6.4 m
二.填空题(共6小题,4*6=24)
11. 写出一个在三视图中左视图与主视图完全相同的几何体:______________.
12. 左图的三棱柱的三视图如右图所示,已知△EFG中,EF=8 cm,EG=12 cm,∠EFG=45°,则AB的长为________cm.
13. 一个几何体的三视图如图所示(其中标注的a,b,c为相应的边长),则这个几何体的体积是________.
14. 一个几何体的三视图如图所示,那么这个几何体的侧面积是________ (结果保留π)
15.如图,四个几何体中,它们各自的三个视图(主视图、左视图和俯视图)有两个相同,而另外一个不同的几何体是________ .(填写序号)
16.如图是一个正方体的展开图,如果将它折成一个正方体,相对面上的数相等,则x+y的值为________.
三.解答题(共5小题, 56分)
17.(6分) 如图所示零件的三视图对吗?把不正确的地方改正过来.
18.(8分) 某校墙边有甲、乙两根木杆,已知乙木杆的高度为1.5m.
(1)某一时刻甲木杆在阳光下的影子如图所示,画出此时乙木杆的影子DF.
(2)△ABC∽△DEF,如果测得甲、乙木杆的影子长分别为1.6m和1m,那么甲木杆的高度是多少?
19.(8分) (1)如图是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图的名称;
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
___________ ____________
20.(10分) 如图,不透明圆锥体DEC放在地面上,在A处灯光照射下形成影子,设BP过底面圆的圆心,已知圆锥体的高为2 m,底面半径为2 m,BE=4 m.
(1)求∠B的度数;
(2)若∠ACP=2∠B,求光源A距地面的高度.(答案用含根号的式子表示)
21.(12分) 我国《道路交通安全法》第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”.如图,一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3 m,驾驶员与车头的距离是0.8 m,这时汽车车头与斑马线的距离x是多少?
22.(12分) 小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
参考答案
1-5CCDAD 6-10CCAAB
11.正方体(答案不唯一)
12.4
13. abc
14. 6π
15. ③④
16. 11
17.三视图都不对,应改为:
18.(1)解:如图所示,DF是乙木杆的影子
(2)解:∵△ABC∽△DEF, ∴ ,即 ,解得AB=2.4m.答:甲木杆的高度是2.4m
19.解:(1)主视图,俯视图
(2)S表=2×(8×5+8×2+5×2)+4×π×6
=2×(8×5+8×2+5×2)+4×3.14×6
=207.36(cm2).
20.解:(1)设DF为圆锥DEC的高,交BC于点F.由已知得BF=BE+EF=6 m,DF=2m,∴tanB===,∴∠B=30°
(2)过点A作AH⊥BP于点H,∵∠ACP=2∠B=60°,∴∠BAC=30°,∴AC=BC=8 m,在Rt△ACH中,AH=AC·sin∠ACP=8×=4(m),∴光源A距地面的高度为4 m
21.解:如图所示,延长AB交两条虚线于E,F.∵CD∥AB,∴∠CAB=30°,∠CBF=60°,∴∠BCA=60°-30°=30°,即∠BAC=∠BCA,∴BC=AB=3 m.在Rt△BCF中,BC=3 m,∠CBF=60°,∴BF=BC=1.5 m,故x=BF-EF=1.5-0.8=0.7(m).答:这时汽车车头与斑马线的距离x是0.7 m.
22. 解(1)小明共剪了8条棱,故答案为:8.
(2)如图,四种情况.
(3)∵长方体纸盒的底面是一个正方形,∴设最短的棱长高为acm,则长与宽相等为5acm,∵长方体纸盒所有棱长的和是880cm,∴4(a+5a+5a)=880,解得a=20cm,∴这个长方体纸盒的体积为:20×100×100=200000立方厘米
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 下列四个几何体中,主视图为圆的是( )
2. 圆形物体在阳光下的投影不可能是( )
A.圆形 B.线段
C.矩形 D.椭圆
3. 如果阳光斜射在地面上,一张矩形纸片在地面上的影子不可能是( )
A. 矩形 B. 线段
C. 平行四边形 D. 一个点
4. 如图是某工厂要设计生产的正六棱柱形密封罐的立体图形,它的主视图是( ).
A B C D
5. 下列四个几何体中,左视图为圆的是( )
A B C D
6. 一个碗如图所示摆放,则它的俯视图是( )
A B C D
7. 一个几何体的三视图如图所示,则该几何体的形状可能是( )
A B C D
8. 学校小卖部货架上摆放着若干盒某品牌方便面,它们的三视图如图所示,则货架上的方便面至少有( )
A.7盒 B.8盒 C.9盒 D.10盒
9.由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示,俯视图的方格中的字母和数字表示该位置上小正方体的个数,则以下说法正确的是( )
A.x=1或2,y=3 B.x=1或2,y=1或3
C.x=1,y=1或3 D.x=2,y=1或3
10. 某数学课外活动小组想利用树影测量树高,他们在同一时刻测得一身高为1.5 m的同学的影长为1.35 m,由于大树靠近一幢建筑物,因此树影的一部分落在建筑物上,如图,他们测得地面部分的影长为3.6 m,建筑物上的影长为1.8 m,则树的高度为( )
A.5.4 m B.5.8 m C.5.22 m D.6.4 m
二.填空题(共6小题,4*6=24)
11. 写出一个在三视图中左视图与主视图完全相同的几何体:______________.
12. 左图的三棱柱的三视图如右图所示,已知△EFG中,EF=8 cm,EG=12 cm,∠EFG=45°,则AB的长为________cm.
13. 一个几何体的三视图如图所示(其中标注的a,b,c为相应的边长),则这个几何体的体积是________.
14. 一个几何体的三视图如图所示,那么这个几何体的侧面积是________ (结果保留π)
15.如图,四个几何体中,它们各自的三个视图(主视图、左视图和俯视图)有两个相同,而另外一个不同的几何体是________ .(填写序号)
16.如图是一个正方体的展开图,如果将它折成一个正方体,相对面上的数相等,则x+y的值为________.
三.解答题(共5小题, 56分)
17.(6分) 如图所示零件的三视图对吗?把不正确的地方改正过来.
18.(8分) 某校墙边有甲、乙两根木杆,已知乙木杆的高度为1.5m.
(1)某一时刻甲木杆在阳光下的影子如图所示,画出此时乙木杆的影子DF.
(2)△ABC∽△DEF,如果测得甲、乙木杆的影子长分别为1.6m和1m,那么甲木杆的高度是多少?
19.(8分) (1)如图是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图的名称;
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
___________ ____________
20.(10分) 如图,不透明圆锥体DEC放在地面上,在A处灯光照射下形成影子,设BP过底面圆的圆心,已知圆锥体的高为2 m,底面半径为2 m,BE=4 m.
(1)求∠B的度数;
(2)若∠ACP=2∠B,求光源A距地面的高度.(答案用含根号的式子表示)
21.(12分) 我国《道路交通安全法》第四十七条规定“机动车行经人行横道时,应当减速行驶;遇行人通过人行横道,应当停车让行”.如图,一辆汽车在一个十字路口遇到行人时刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3 m,驾驶员与车头的距离是0.8 m,这时汽车车头与斑马线的距离x是多少?
22.(12分) 小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
参考答案
1-5CCDAD 6-10CCAAB
11.正方体(答案不唯一)
12.4
13. abc
14. 6π
15. ③④
16. 11
17.三视图都不对,应改为:
18.(1)解:如图所示,DF是乙木杆的影子
(2)解:∵△ABC∽△DEF, ∴ ,即 ,解得AB=2.4m.答:甲木杆的高度是2.4m
19.解:(1)主视图,俯视图
(2)S表=2×(8×5+8×2+5×2)+4×π×6
=2×(8×5+8×2+5×2)+4×3.14×6
=207.36(cm2).
20.解:(1)设DF为圆锥DEC的高,交BC于点F.由已知得BF=BE+EF=6 m,DF=2m,∴tanB===,∴∠B=30°
(2)过点A作AH⊥BP于点H,∵∠ACP=2∠B=60°,∴∠BAC=30°,∴AC=BC=8 m,在Rt△ACH中,AH=AC·sin∠ACP=8×=4(m),∴光源A距地面的高度为4 m
21.解:如图所示,延长AB交两条虚线于E,F.∵CD∥AB,∴∠CAB=30°,∠CBF=60°,∴∠BCA=60°-30°=30°,即∠BAC=∠BCA,∴BC=AB=3 m.在Rt△BCF中,BC=3 m,∠CBF=60°,∴BF=BC=1.5 m,故x=BF-EF=1.5-0.8=0.7(m).答:这时汽车车头与斑马线的距离x是0.7 m.
22. 解(1)小明共剪了8条棱,故答案为:8.
(2)如图,四种情况.
(3)∵长方体纸盒的底面是一个正方形,∴设最短的棱长高为acm,则长与宽相等为5acm,∵长方体纸盒所有棱长的和是880cm,∴4(a+5a+5a)=880,解得a=20cm,∴这个长方体纸盒的体积为:20×100×100=200000立方厘米
