第5章数据的频数分布练习题2020-2021学年湖南省各地湘教版八年级数学下册期末试题选编(Word版含解析)
文档属性
| 名称 | 第5章数据的频数分布练习题2020-2021学年湖南省各地湘教版八年级数学下册期末试题选编(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 485.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 21:05:57 | ||
图片预览




文档简介
湘教版八年级数学下册第5章:数据的频数分布练习题
一、单选题
1.(2021·湖南洪江·八年级期末)小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:
通话时间 x/min 0频数 (通话次数) 20 16 9 5
则通话时间不超过15 min的频率为( )
A.0.1 B.0.4 C.0.5 D.0.9
2.(2021·湖南宁远·八年级期末)某班50名学生的身高被分为5组,第1至4组的频数分别为7、12、13、8,则第5组的频率是( )
A. B. C. D.
3.(2021·湖南绥宁·八年级期末)一个人做“抛硬币”的游戏,正面出现4次,反面出现了6次,正确说法为( )
A.出现正面的频率是4 B.出现反面的频率是6
C.出现反面的频率是60% D.出现正面的频数是40%
4.(2021·湖南岳阳·八年级期末)小明3分钟共投篮80次,进了50个球,则小明进球的频率是( ).
A.80 B.50 C.1.6 D.0.625
5.(2021·湖南·张家界市民族中学八年级期末)大课间活动在我市各校蓬勃开展.某班大课间活动抽查了20名学生每分钟跳绳次数,获得如下数据(单位:次):50,63,77,83,87,88,89,91,93,100,102,111,117,121,130,133,146,158,177,188.则跳绳次数在90~110这一组的频率是( )
A.0.1 B.0.2 C.0.3 D.0.7
6.(2021·湖南零陵·八年级期末)一次数学测试后,某班m名学生的成绩被分为5组,第1~4组的频数分别是10,11,7,12,第5组的频率为0.2,则m的值为( )
A.40 B.48 C.50 D.52
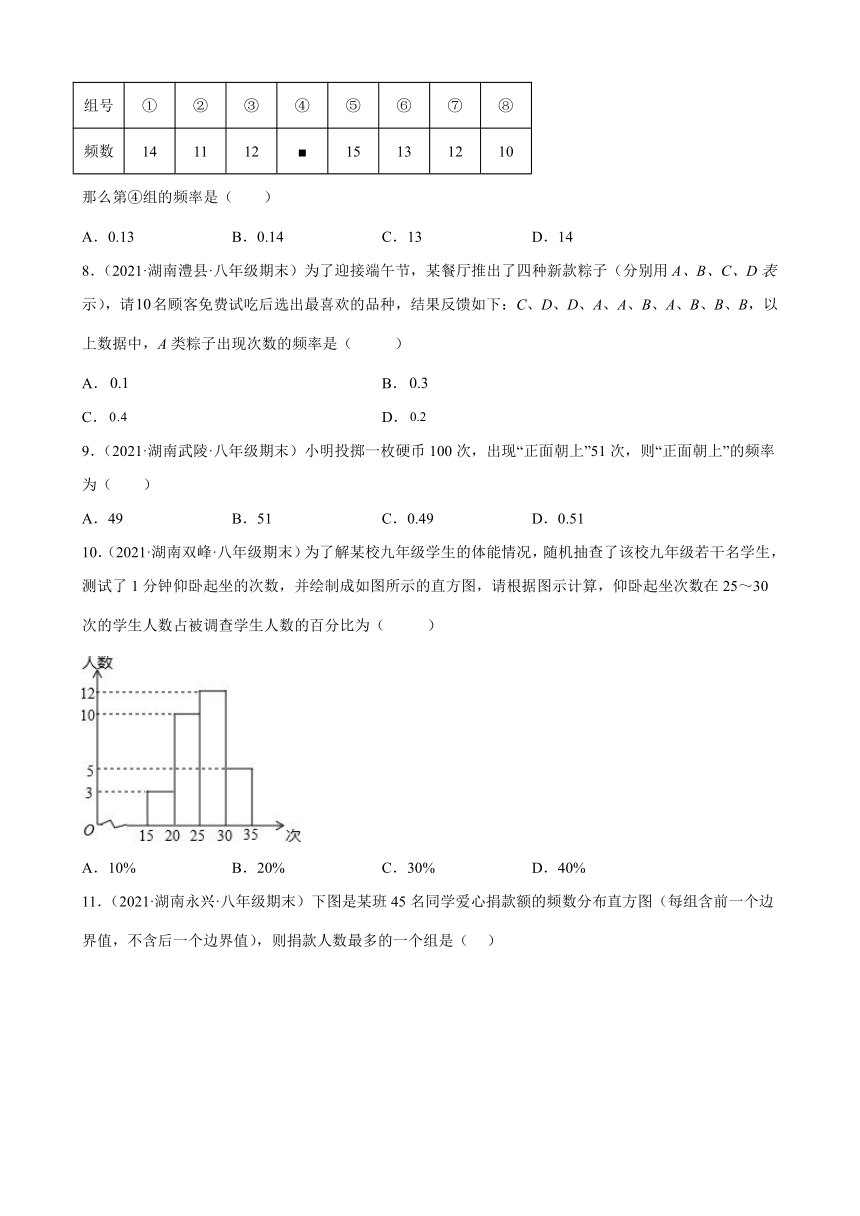
7.(2021·湖南·茶陵县教育教学研究室八年级期末)将样本容量为100的样本编制成组号①~⑧的八个组,简况如下表所示:
组号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧
频数 14 11 12 ■ 15 13 12 10
那么第④组的频率是( )
A.0.13 B.0.14 C.13 D.14
8.(2021·湖南澧县·八年级期末)为了迎接端午节,某餐厅推出了四种新款粽子(分别用A、B、C、D表示),请名顾客免费试吃后选出最喜欢的品种,结果反馈如下:C、D、D、A、A、B、A、B、B、B,以上数据中,A类粽子出现次数的频率是( )
A. B.
C. D.
9.(2021·湖南武陵·八年级期末)小明投掷一枚硬币100次,出现“正面朝上”51次,则“正面朝上”的频率为( )
A.49 B.51 C.0.49 D.0.51
10.(2021·湖南双峰·八年级期末)为了解某校九年级学生的体能情况,随机抽查了该校九年级若干名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的直方图,请根据图示计算,仰卧起坐次数在25~30次的学生人数占被调查学生人数的百分比为( )
A.10% B.20% C.30% D.40%
11.(2021·湖南永兴·八年级期末)下图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一个组是( )
A.5~10元 B.10~15元 C.15~20元 D.20~25元
12.(2021·湖南荷塘·八年级期末)小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.①小文同学一共统计了60人;②每天微信阅读不足20分钟的人数有12人;③每天微信阅读30﹣40分钟的人数最多;④每天微信阅读0﹣10分钟的人数最少.根据图中信息,上述说法中正确的是( )
A.①②③④ B.①②③ C.②③④ D.③④
二、填空题
13.(2021·湖南武陵·八年级期末)王老师对本班40个学生所穿校服尺码的数据统计如下:
尺码 S M L XL XXL XXL
频率 0.05 0.1 0.2 0.325 0.3 0.025
则该班学生所穿校服尺码为“L”的人数有________个.
14.(2021·湖南岳阳·八年级期末)已知一组数据有40个,把它分成六组,第一组到第四组的频数分别是5,10,6,7,第五组的频率是0.2,故第六组的频数是_______.
15.(2021·湖南娄底·八年级期末)把容量是64的样本分成8组,从第1组到第4组的频数分别是5,7,11,13,第5组到第7组的频率都是0.125,那么第8组的频率是______.
16.(2021·湖南荷塘·八年级期末)某班女生的体温测试被分成了三组,情况如表所示,则表中m的值是_______.
第一组 第二组 第三组
频数 6 8 m
频率 p q 30%
17.(2021·湖南新化·八年级期末)一次跳远中,成绩在4.05米以上的人有8人,频率为0.4,则参加比赛的运动员共有____人.
18.(2021·湖南宁远·八年级期末)已知10个数据:0、1、1、2、2、2、3、3、3、8,其中3出现的频数是_______.
19.(2021·湖南·茶陵县教育教学研究室八年级期末)在英文单词 believe 中,字母“e”出现的频率是_______.
20.(2021·湖南永兴·八年级期末)现将一组数据:21,25,23,25,27,29,25,30,28,29,26,24,27,25,26,22,24,25,26,28分成五组,其中26.5<x<28.5的频数是____.
21.(2021·湖南隆回·八年级期末)在一串数字“1235362731”中,数字“3”出现的频率为___________.
22.(2021·湖南岳阳·八年级期末)某班50位同学中,1月份出生的频率是0.3,这个班1月份出生的同学有____人.
23.(2021·湖南湘乡·八年级期末)永州市教育部门为了了解全市中小学安全教育情况,对某校进行了“防溺水”安全知识的测试.从七年级随机抽取了50名学生的测试成绩(百分制),整理样本数据,得到下表:
成绩 90≤x≤100 80≤x<90 70≤x<80 60≤x<70 x<60
人数 25 15 5 4 1
根据抽样调查结果,估计该校七年级600名学生中,80分(含80分)以上的学生有________人.
24.(2021·湖南绥宁·八年级期末)如图是某市晚报记者在抽样调查了一些市民用于读书、读报、参加“全民健身运动”等休闲娱乐活动的时间后,绘制的频数分布直方图(共六组),已知从左往右前五组的频率之和为0.94,如果第六组有12个数,则此次抽样的样本容量是_____
25.(2021·湖南洪江·八年级期末)一个容量为80的样本最大值为143,最小值为50,取组距为10,则可以分成________组.
26.(2021·湖南炎陵·八年级期末)统计得到的一组数据的最大值为218,最小值为100,取组距为15,可分成________组.
三、解答题
27.(2021·湖南雨花·八年级期末)某学校开展了防疫知识的宣传教育活动.为了解这次活动的效果,学校从全校1500名学生中随机抽取部分学生进行知识测试(测试满分100分,得分x均为不小于60的整数),并将测试成绩分为四个等第:基本合格(60≤x<70),合格(70≤x<80),良好(80≤x<90),优秀(90≤x≤100),制作了如图统计图(部分信息未给出).
由图中给出的信息解答下列问题:
(1)求测试成绩为合格的学生人数,并补全频数直方图.
(2)求扇形统计图中“良好”所对应的扇形圆心角的度数.
(3)这次测试成绩的中位数是什么等第?
(4)如果全校学生都参加测试,请你根据抽样测试的结果,估计该校获得优秀的学生有多少人?
28.(2021·湖南武陵·八年级期末)2020年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 频数
a
12
b
10
学生立定跳远测试成绩的频数分布直方图
请根据图表中所提供的信息,完成下列问题:
(1)表中________,________;
(2)样本成绩的中位数落在________范围内;
(3)请把频数分布直方图补充完整;
(4)该校共有1200名学生,估计该学校学生立定跳远成绩在范围内的有多少人?
29.(2021·湖南洪江·八年级期末)为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为(分),且,将其按分数段分为五组,绘制出以下不完整表格:
组别 成绩(分) 频数(人数) 频率
一 2 0.04
二 10 0.2
三 14 b
四 a 0.32
五 8 0.16
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有 名学生参加;
(2)直接写出表中a= ,b= ;
(3)请补全下面相应的频数分布直方图;
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 .
30.(2021·湖南醴陵·八年级期末)某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 体重(千克) 人数
A 37.5≤x<42.5 10
B 42.5≤x<47.5 n
C 47.5≤x<52.5 40
D 52.5≤x<57.5 20
E 57.5≤x<62.5 10
请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?
31.(2021·湖南新化·八年级期末)九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量(t) 频数(户) 频率
6 0.12
0.24
16 0.32
10 0.20
4
2 0.04
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
32.(2021·湖南临湘·八年级期末)为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了“汉字听写大赛”.经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,写错或不写不得分.根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下图表:
组别 成绩x分 频数(人数)
第1组 25≤x<30 4
第2组 30≤x<35 8
第3组 35≤x<40 16
第4组 40≤x<45 a
第5组 45≤x<50 10
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
33.(2021·湖南长沙·八年级期末)今年受疫情影响,我市中小学生全体在家线上学习.为了了解学生在家主动锻炼身体的情况,某校随机抽查了部分学生,对他们每天的运动时间进行调查,并将调查统计的结果分为四类:每天运动时间t≤20分钟的学生记为A类,20分钟<t≤40分钟记为B类,40分钟<t≤60分钟记为C类,t>60分钟记为D类.收集的数据绘制如下两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
(1)这次共抽取了_________名学生进行调查统计;
(2)扇形统计图中D类所对应的扇形圆心角大小为_________;
(3)将条形统计图补充完整;
(4)如果该校共有1500名学生,请你估计该校B类学生约有多少人?
34.(2021·湖南宁远·八年级期末)某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x<100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
分数段 频数 频率
60≤x<70 18 0.36
70≤x<80 17 c
80≤x<90 a 0.24
90≤x<100 b 0.06
合计 1
根据以上信息解答下列问题:
(1)统计表中c的值为________;样本成绩的中位数落在分数段________中;
(2)补全频数直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评的作品数量是多少.
35.(2021·湖南双峰·八年级期末) 某校为加强学生安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分100分)进行统计,请根据尚为完成的频率和频数分布直方图,解答下列问题:
分数段 频数 频率
50.5~60.5 16 0.08
60.5~70.5 40 0.2
70.5~80.5 50 0.25
80.5~90.5 m 0.35
90.5~100.5 24 n
(1)这次抽取了______名学生的竞赛成绩进行统计,其中m=______,n=______;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
36.(2021·湖南鹤城·八年级期末)“新型冠状病毒肺炎”疫情牵动着亿万国人的心,为进一步加强疫情防控工作,某学校利用网络平台进行疫情防控知识测试.小青从全体学生中随机抽取部分同学的分数(得分取正整数,满分为100分)进行统计,以下是根据抽取同学的分数制作的不完整的频率分布表和频率分布直方图,请根据图表,回答下列问题:
组别 分组 频数 频率
1 9 0.18
2
3 21 0.42
4 0.06
5 2
(1)根据上表填空:a= ,b= ,m= ;
(2)若小青的测试成绩是抽取的同学成绩的中位数,则小青的测试成绩在什么范围内?
(3)若规定:得分在90≤x≤100的为“优秀”,若小青所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加决赛,请问共有多少名学生被选拔参加决赛?
37.(2021·湖南绥宁·八年级期末)垃圾分类是一项“利国利民”的民生工程,需要全社会的共同参与.某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾,如图表是七年级各班一周收集的可回收垃圾的重量(千克)的频数表和频数分布直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的重量的频数表
组别(kg) 频数
4.0~4.5 2
4.5~5.0 a
5.0~5.5 3
5.5~6.0 1
(1)求a的值
(2)已知收集的可回收垃圾以1.1元/kg被回收,该年级这周收集的可回收垃圾被回收后所得金额能否达到60元?
38.(2021·湖南永兴·八年级期末)某班学生的期中成绩(成绩为整数)的频数分布表如下,请根据表中提供的信息回答下列问题:
分组 频数 频率
49.5<x<59.5 2 0.04
59.5<x<69.5 6 m
69.5<x<79.5 n 0.44
79.5<x<89.5 15 0.3
89.5<x<99.5 5 p
合计 q 1.0
(1)m= ,n= ,p= ,q= ;
(2)在表内,频率最小的一组的成绩范围是 ;
(3)成绩优秀的学生有 人(成绩大于或等于80分为优秀).
(4)你认为该班学生的学习成绩怎么样?根据数据说明你的看法.
试卷第1页,共3页
参考答案:
1.D
【分析】
用不超过15分钟的通话时间除以所有的通话时间即可求得通话时间不超过15分钟的频率.
【详解】
解:∵不超过15分钟的通话次数为20+16+9=45次,通话总次数为20+16+9+5=50次,
∴通话时间不超过15min的频率为=0.9,
故选D.
【点睛】
本题考查了频数分布表的知识,解题的关键是了解频率=频数÷样本容量,难度不大.
2.C
【分析】
先求得第5组的频数,再除以总学生数即可.
【详解】
由第5组频数为:,得第五组的频率为.
故选:C.
【点睛】
此题考查频数与频率的关系,知道所有频数之和为样本容量及每组频率等于其频数与样本容量的商是关键.
3.C
【分析】
根据频率的计算方法判断各个选项.
【详解】
解:A、应为:出现正面的频数是4,错误,不符合题意;
B、应为:出现反面的频数是6,错误,不符合题意;
C、正确,符合题意;
D、出现正面的频率是40%,错误,不符合题意.
故选:C.
【点睛】
本题考查了频率以及频数的概念,熟知频率的计算方法是解本题的关键.
4.D
【详解】
试题分析:频率等于频数除以数据总和,∵小明共投篮80次,进了50个球,∴小明进球的频率=50÷80=0.625,故选D.
考点:频数与频率.
5.B
【详解】
跳绳次数在90~110之间的数据有91,93,100,102四个,故频率为 =0.2.
故选B.
6.C
【分析】
根据频率公式:频率=频数÷总数即可求解.
【详解】
解:根据题意,得=0.2,
解得m=50.
故选:C.
【点睛】
本题考查了频率的计算公式,理解公式是解题的关键.
7.A
【分析】
先求出该组的频数,再利用频率计算公式求出答案.
【详解】
解:第④组的频数是100-14-11-12-15-13-12-10=13,
∴第④组的频率是,
故选:A.
【点睛】
此题考查频率的计算公式:频数除以总数,熟记公式是解题的关键.
8.B
【分析】
根据频率=求解即可.
【详解】
解:由题意可知,共反馈10种结果,其中A出现3次,
∴A类粽子出现次数的频率是
故选:B
【点睛】
本题考查频率的概念,掌握频率=是本题的解题关键.
9.D
【分析】
根据频率=“正面朝上的频数”÷投掷硬币的总数,即可解答.
【详解】
解:∵小明投掷一枚硬币100次,出现“正面朝上”51次,
∴“正面朝上”的频率为:,
故选:D.
【点睛】
本题考查了频率的定义,熟知定义是解题的关键.
10.D
【分析】
根据频率直方图可以知道被调查的总人数,又在要求的范围可以很直观地由图形看出,即可得出百分比.
【详解】
解:由频率直方图可以得出,被调查的总人数=3+10+12+5=30.
又仰卧起坐次数在25~30次的学生人数为12,故百分比为40%,
故选D.
【点睛】
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
11.C
【详解】
试题分析:根据图形所给出的数据可得:
∵15﹣20元的有20人,人数最多,∴捐款人数最多的一组是15﹣20元.
故选C.
考点:频数分布直方图.
12.C
【分析】
根据直方图表示的意义求得统计的总人数,以及每组的人数即可判断.
【详解】
解:①小文同学一共统计了4+8+14+20+16+12=74(人),故①说法错误,不符合题意;
②每天微信阅读不足20分钟的人数有4+8=12(人),故②说法正确,符合题意;
③每天微信阅读30﹣40分钟的人数最多,故③说法正确,符合题意;
④每天微信阅读0﹣10分钟的人数最少,故④说法正确,符合题意.
故选:C.
【点睛】
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
13.8
【分析】
直接用尺码L的频率乘以班级总人数即可求出答案.
【详解】
解:由表可知尺码L的频率的0.2,又因为班级总人数为40,
所以该班学生所穿校服尺码为“L”的人数有400.2=8.
故答案是:8.
【点睛】
此题主要考查了频数与频率,关键是掌握频数是指每个对象出现的次数.频率是指每个对象出现的次数与总次数的比值(或者百分比).即频率=频数÷总数.
14.4
【分析】
首先根据频率的计算公式求得第五组的频数,然后利用总数减去其它组的频数即可求解.
【详解】
第五组的频数是40×0.2=8,
则第六组的频数是40-5-10-6-7-8=4.
故答案是:4.
【点睛】
本题是对频率、频数灵活运用的综合考查.
注意:每个小组的频数等于数据总数减去其余小组的频数,即各小组频数之和等于数据总和.
15.0.0625
【分析】
利用频率与频数的关系得出第1组到第4组的频率,进而得出第8组的频率.
【详解】
解:∵把容量是64的样本分成8组,从第1组到第4组的频数分别是5,7,11,13,
∴第1组到第4组的频率是:(5+7+11+13)0.5625
∵第5组到第7组的频率是0.125,
第8组的频率是:1- 0.5625-0.125= 0.0625
故答案为: 0.0625.
【点睛】
此题主要考查了频数与频率,正确求出第5组到第7组的频数是解题关键.
16.6
【分析】
根据各小组的频率之和等于1,即可得出第一组与第二组的频率和,然后求出数据总数,从而求出m的值.
【详解】
解:∵第一组与第二组的频率之和为1-30%=70%,
∴该班男生的总人数为(6+8)÷70%=20,
∴m= 20×30%=6.
故答案为:6.
【点睛】
本题主要考查了频数与频率,频率是指每个对象出现的次数与总次数的比值(或者百分比),即频率=频数÷总数.
17.20
【分析】
根据频率的计算公式即可得到答案.
【详解】
解:
所以可得参加比赛的人数为20人.
故答案为20.
【点睛】
本题主要考查频率的计算公式,这是数据统计的重点知识,必须掌握.
18.3.
【分析】
直接利用频数的定义分析得出答案.
【详解】
解:10个数据:0、1、1、2、2、2、3、3、3、8,其中3出现了3次,故3出现的频数是3.
故答案为3.
【点睛】
本题主要考查了频数的定义,正确把握频数的定义是解题的关键.
19.
【分析】
先求出英文单词believe总的字母个数和e的个数,再根据握频率=进行计算即可.
【详解】
∵英文单词believe共有7个字母,其中有3个e,
∴字母“e”出现的频率是;
故答案为:.
【点睛】
此题考查频数与频率,解题关键在于掌握频率的计算公式即可.
20.4
【分析】
先将各数据划记到对应的小组,再正确数出第四组26.5~28.5的频数即可.
【详解】
解:这组数据中26.5<x<28.5的数据,即是数据27、28出现的次数,
通过统计数据27、28共出现4次,
故答案为:4.
【点睛】
本题考查频率、频数的概念,一般称落在不同小组中的数据个数为该组的频数,频数与数据总数的比值为频率.
21.
【分析】
根据频率=频数÷总数求解即可得到答案.
【详解】
解:∵在一串数字“1235362731”中,数字“3”出现的次数为3次,数字数目为10,
∴数字“3”出现的频率,
故答案为:.
【点睛】
本题主要考查了频率的计算,解题的关键在于能够熟记频率=频数÷总数.
22.15
【分析】
根据频率的求法,频率=频数÷数据总和,计算可得答案.
【详解】
解:50×0.3=15人,
故答案为:15.
【点睛】
本题主要考查了频率的计算公式,是需要识记的内容.
23.480
【分析】
用七年级的学生总数乘以样本中80分以上的比例即可得到答案.
【详解】
600×=480(人)
故答案为:480.
【点睛】
本题考查了频数分布图、用样本估计总体,解答本题的关键是明确题意,由样本数据可以估计总体;
24.200
【分析】
根据频数分布直方图中各组的频率总和等于1,计算可得第六组的频率,根据第六组的频数,进而根据频率的计算公式计算可得答案.
【详解】
解:根据频数分布直方图中每一组内的频率总和等于1,可知第六组的频率为1﹣0.94=0.06,又因为第六组有12个数,所以此次抽样的样本容量是12÷0.06=200.
故答案为:200.
【点睛】
本题考查了读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
25.10
【分析】
根据组距,最大值、最小值、组数以及样本容量的关系进行计算即可.
【详解】
解:(143-50)÷10=9.3≈10,
故可以分成10组
故答案为:10.
【点睛】
本题考查频数分布直方图的制作方法,理解组距、组数,极差以及样本容量之间的关系是正确解答的关键.
26.
【分析】
根据组数=(最大值-最小值)÷组距计算,注意小数部分要进位.
【详解】
解:在样本数据中最大值为218,最小值为100,它们的差是218-100=118,
已知组距为15,由于118÷15, 故可以分成8组.
故答案为:8.
【点睛】
本题考查的是组数的计算,数据分成的组的个数称为组数是解题的关键,注意小数部分要进位.
27.(1)见解析;(2)144°;(3)这次测试成绩的中位数的等第是良好;(4)估计该校获得优秀的学生有300人
【分析】
(1)根据基本合格人数已经百分比求出总人数即可解决问题;
(2)根据圆心角=360°×百分比计算即可;
(3)根据中位数的定义判断即可;
(4)利用样本估计总体的思想解决问题即可.
【详解】
解:(1)30÷15%=200(人),
200﹣30﹣80﹣40=50(人),
直方图如图所示:
;
(2)“良好”所对应的扇形圆心角的度数=360°×=144°;
(3)这次成绩按从小到大的顺序排列,中位数在80分-90分之间,
∴这次测试成绩的中位数的等第是良好;
(4)1500×=300(人),
答:估计该校获得优秀的学生有300人.
【点睛】
本题考查频数分布直方图,样本估计总体,扇形统计图,中位数等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
28.(1),;(2);(3)详见解析;(4)240人
【分析】
(1)根据频数分布直方图可以求得a的值,再根据样本容量求出b的值.
(2)结合中位数的求法可以求出中位数落在哪一组.
(3)根据(1)中的结果可以将频数分布直方图补充完整.
(4)根据频数分步表中的数据可以求出该学校学生立定跳远成绩在范围内的有多少人.
【详解】
解(1)由统计图可得,;
(2)有50名学生进行测试,第25和26名的成绩和的平均数为中位数
样本成绩的中位数落在范围内;
(3)由(1)知,,补全的频数分布直方图如右图所示;
学生立定跳远测试成绩的频数分布直方图
(4)(人),
答:估计该学校学生立定跳远成绩在范围内有240人.
【点睛】
本题考查频数分步表、频数分步直方图、中位数、用样本估计总体,解答本题的关键是明确题意,利用数形结合思想解答.
29.(1)50;(2)a=16,b=0.28;(3)答案见解析;(4)48%.
【详解】
试题分析:(1)根据第一组别的人数和百分比得出样本容量;(2)根据样本容量以及频数、频率之间的关系得出a和b的值,(3)根据a的值将图形补全;(4)根据图示可得:优秀的人为第四和第五组的人,将两组的频数相加乘以100%得出答案.
试题解析:(1)2÷0.04=50
(2)50×0.32=16 14÷50=0.28
(3)
(4)(0.32+0.16)×100%=48%
考点:频数分布直方图
30.(1)①100,②20,③144;(2)被被抽取同学的平均体重为50千克;(3)七年级学生体重低于47.5千克的学生大约有300人.
【分析】
(1)①m=20÷20%=100,②n=100-10-40-20-10=20,③c=×360°=144°;
(2)被抽取同学的平均体重为:
.(千克);
(3)七年级学生体重低于47.5千克的学生1000×30%=300(人).
【详解】
(1)①100,②20,③144;
(2)被抽取同学的平均体重为:
.
答:被抽取同学的平均体重为50千克.
(3).
答:七年级学生体重低于47.5千克的学生大约有300人.
【点睛】
本题考查的是频数分布表和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.频数分布表能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
31.(1)见解析
(2)该小区用水量不超过15t的家庭占被调查家庭总数的百分比为68﹪.
(3)该小区月均用水量超过20t的家庭大约有120户.
【分析】
频数(率)分布表,频数分布直方图,频数、频率和总量的关系,用样本估计总体.
(1)根据0<x≤5中频数为6,频率为0.12,则调查总户数为6÷0.12=50,进而得出在5<x≤10范围内的频数以及在20<x≤25范围内的频率.
(2)根据(1)中所求即可得出不超过15t的家庭总数即可求出,不超过15t的家庭占被调查家庭总数的百分比.
(3)根据样本数据中超过20t的家庭数,即可得出1000户家庭超过20t的约家庭数.
【详解】
解:(1)如图所示:
根据0<x≤5中频数为6,频率为0.12,则6÷0.12=50,
∴月均用水量5<x≤10的频数:50×0.24=12户;
月均用水量20<x≤25的频率:4÷50=0.08.
∴统计中的频数分布表和不完整的频数分布直方图,补充如下;
月均用水量(t) 频数(户) 频率
6 0.12
12 0.24
16 0.32
10 0.20
4 0.08
2 0.04
(2)用水量不超过15吨是前三组,
∴该小区用水量不超过15t的家庭占被调查家庭总数的百分比为
(0.12+0.24+0.32)×100﹪=68﹪.
(3)用水量超过20t是最后两组,
∴该小区月均用水量超过20t的家庭大约有:1000×(0.04+0.08)=120(户).
32.(1)a=12;(2)补图见解析;(3)本次测试的优秀率是44%.
【分析】
(1)用总数50减去其他各组的频数即可求得a的值;
(2)由(1)的结果即可把频数分布直方图补充完整;
(3)由百分比的意义即可求解.
【详解】
(1)a=50﹣4﹣8﹣14﹣10=12;
(2)如图所示:
(3)本次测试的优秀率是:(12+10)÷50×100%=44%.
33.(1)50;(2)36°;(3)图见解析;(4)该校B类学生约有660人.
【分析】
(1)根据A类的条形统计图和扇形统计图信息即可得;
(2)先根据题(1)的结论求出D类学生的人数,再求出D类学生的人数占比,然后乘以360°可得圆心角的大小;
(3)由(2)即可得补充条形统计图;
(4)先求出B类学生的人数占比,再乘以1500即可得.
【详解】
(1)这次调查共抽取的学生人数为15÷30%=50(名)
故答案为:50;
(2)D类学生的人数为50 15 22 8=5(名)
则D类学生的人数占比为×100%=10%
D类所对应的扇形圆心角大小为360°×10%=36°
(3)条形统计图补全如下:
(4)B类学生的人数占比为×100%=44%
则1500×44%=660(人)
答:该校B类学生约有660人.
【点睛】
本题考查了条形统计图和扇形统计图的信息关联、画条形统计图等知识点,熟练掌握统计调查的相关知识是解题关键.
34.(1)0.34;70≤x<80;(2)见解析;(3) 180幅.
【分析】
(1)由60≤x<70频数和频率求得总数,根据频率=频数÷总数求得a、b、c的值,由中位数定义求解可得;
(2)根据(1)中所求数据补全图形即可得;
(3)总数乘以80分以上的频率即可.
【详解】
解:(1)本次调查的作品总数为18÷0.36=50(幅),
则c=17÷50=0.34,a=50×0.24=12,b=50×0.06=3,
其中位数为第25、26个数的平均数,
∴中位数落在70≤x<80中,
故答案为0.34,70≤x<80;
(2)补全图形如下:
(3)600×(0.24+0.06)=180(幅),
答:估计全校被展评作品数量是180幅.
【点睛】
本题考查读频数(率)分布直方图的能力和利用统计图获取信息的能力,以及条形统计图;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
35.(1)200,70,0.12;(2)详见解析;(3)420
【分析】
(1)根据50.5~60.5的频数和频率先求出总数,再根据频数、频率和总数之间的关系分别求出m、n的值;
(2)根据(1)的结果可补全统计图;
(3)用全校的总人数乘以成绩在70分以下(含70分)的学生所占的百分比,即可得出答案.
【详解】
解:(1)根据题意得:=200(名),
m=200×0.35=70(名),
n==0.12;
故答案为:200,70,0.12;
(2)根据(1)补图如下:
(3)根据题意得:
1500×(0.08+0.2)=420(人),
答:该校安全意识不强的学生约有420人.
【点睛】
此题主要考查了频数分布直方图、频数分布表、利用样本估计总体,关键是读懂频数分布直方图,能利用统计图获取信息;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
36.(1)3,0.3,15,(2);(3)共有24名学生被选拔参加决赛.
【分析】
(1)根据频数、频率、总数之间的关系一一解决问题即可;
(2)根据中位数的定义即可判断;
(3)用样本估计总体的思想解决问题即可.
【详解】
解:(1)(人.
,,.
故答案为:3,0.3,15
(2)抽取的学生共有50名,中位数是第25、26个数据的平均数,第25、26个数据在第3组,所以小青的测试成绩在范围内;
(3)(人)
答:共有24名学生被选拔参加决赛.
【点睛】
本题考查频数分布直方图、频数分布表、中位数的定义等知识,解题的关键是熟练掌握基本知识.
37.(1)a=4;(2)不能达到
【分析】
(1)由频数分布直方图可得4.5~5.0的频数a的值;
(2)先求出该年级这周收集的可回收垃圾的质量的最大值,再乘以单价即可得出答案.
【详解】
解:(1)由频数分布直方图可知4.5~5.0的频数a=4;
(2)∵该年级这周收集的可回收垃圾的质量小于4.5×2+5.0×4+5.5×3+6.0=51.5(kg),
∴该年级这周收集的可回收垃圾被回收后所得金额小于51.5×1.1=56.65(元),
∴该年级这周收集的可回收垃圾被回收后所得金额不能达到60元.
【点睛】
本题主要考查了频数分布表,频数分布直方图,解题的关键在于能够准确读懂题意.
38.(1)0.12,22,0.1,50;(2)49.5<x<59.5;(3)20;(4)见解析
【分析】
(1)先根据49.5<x<59.5的频数及其频率求解可得样本容量q的值,再根据频率=频数÷样本容量和频数=样本容量×频率求解即可;
(2)根据以上所求结果即可得出答案;
(3)将79.5<x<89.5、89.5<x<99.5的频数相加即可;
(4)答案不唯一,合理均可.
【详解】
解:(1)∵q=2÷0.04=50,
∴m=6÷50=0.12,
n=50×0.44=22,
p=5÷50=0.1,
故答案为:0.12、22、0.1、50;
(2)在表内,频率最小的一组的成绩范围是49.5<x<59.5,
故答案为:49.5<x<59.5;
(3)成绩优秀的学生人数为15+5=20(人),
故答案为:20;
(4)成绩很好,
理由:优秀人数多,有20人(答案不唯一).
【点睛】
本题主要考查了频数分布表,在统计数据时,经常把数据按照不同的范围分成几个组,分成的组的个数称为组数,每一组两个端点的差称为组距,称这样画出的统计图表为频数分布表.
答案第1页,共2页
一、单选题
1.(2021·湖南洪江·八年级期末)小明统计了他家今年5月份打电话的次数及通话时间,并列出了如下的频数分布表:
通话时间 x/min 0
则通话时间不超过15 min的频率为( )
A.0.1 B.0.4 C.0.5 D.0.9
2.(2021·湖南宁远·八年级期末)某班50名学生的身高被分为5组,第1至4组的频数分别为7、12、13、8,则第5组的频率是( )
A. B. C. D.
3.(2021·湖南绥宁·八年级期末)一个人做“抛硬币”的游戏,正面出现4次,反面出现了6次,正确说法为( )
A.出现正面的频率是4 B.出现反面的频率是6
C.出现反面的频率是60% D.出现正面的频数是40%
4.(2021·湖南岳阳·八年级期末)小明3分钟共投篮80次,进了50个球,则小明进球的频率是( ).
A.80 B.50 C.1.6 D.0.625
5.(2021·湖南·张家界市民族中学八年级期末)大课间活动在我市各校蓬勃开展.某班大课间活动抽查了20名学生每分钟跳绳次数,获得如下数据(单位:次):50,63,77,83,87,88,89,91,93,100,102,111,117,121,130,133,146,158,177,188.则跳绳次数在90~110这一组的频率是( )
A.0.1 B.0.2 C.0.3 D.0.7
6.(2021·湖南零陵·八年级期末)一次数学测试后,某班m名学生的成绩被分为5组,第1~4组的频数分别是10,11,7,12,第5组的频率为0.2,则m的值为( )
A.40 B.48 C.50 D.52
7.(2021·湖南·茶陵县教育教学研究室八年级期末)将样本容量为100的样本编制成组号①~⑧的八个组,简况如下表所示:
组号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧
频数 14 11 12 ■ 15 13 12 10
那么第④组的频率是( )
A.0.13 B.0.14 C.13 D.14
8.(2021·湖南澧县·八年级期末)为了迎接端午节,某餐厅推出了四种新款粽子(分别用A、B、C、D表示),请名顾客免费试吃后选出最喜欢的品种,结果反馈如下:C、D、D、A、A、B、A、B、B、B,以上数据中,A类粽子出现次数的频率是( )
A. B.
C. D.
9.(2021·湖南武陵·八年级期末)小明投掷一枚硬币100次,出现“正面朝上”51次,则“正面朝上”的频率为( )
A.49 B.51 C.0.49 D.0.51
10.(2021·湖南双峰·八年级期末)为了解某校九年级学生的体能情况,随机抽查了该校九年级若干名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的直方图,请根据图示计算,仰卧起坐次数在25~30次的学生人数占被调查学生人数的百分比为( )
A.10% B.20% C.30% D.40%
11.(2021·湖南永兴·八年级期末)下图是某班45名同学爱心捐款额的频数分布直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一个组是( )
A.5~10元 B.10~15元 C.15~20元 D.20~25元
12.(2021·湖南荷塘·八年级期末)小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.①小文同学一共统计了60人;②每天微信阅读不足20分钟的人数有12人;③每天微信阅读30﹣40分钟的人数最多;④每天微信阅读0﹣10分钟的人数最少.根据图中信息,上述说法中正确的是( )
A.①②③④ B.①②③ C.②③④ D.③④
二、填空题
13.(2021·湖南武陵·八年级期末)王老师对本班40个学生所穿校服尺码的数据统计如下:
尺码 S M L XL XXL XXL
频率 0.05 0.1 0.2 0.325 0.3 0.025
则该班学生所穿校服尺码为“L”的人数有________个.
14.(2021·湖南岳阳·八年级期末)已知一组数据有40个,把它分成六组,第一组到第四组的频数分别是5,10,6,7,第五组的频率是0.2,故第六组的频数是_______.
15.(2021·湖南娄底·八年级期末)把容量是64的样本分成8组,从第1组到第4组的频数分别是5,7,11,13,第5组到第7组的频率都是0.125,那么第8组的频率是______.
16.(2021·湖南荷塘·八年级期末)某班女生的体温测试被分成了三组,情况如表所示,则表中m的值是_______.
第一组 第二组 第三组
频数 6 8 m
频率 p q 30%
17.(2021·湖南新化·八年级期末)一次跳远中,成绩在4.05米以上的人有8人,频率为0.4,则参加比赛的运动员共有____人.
18.(2021·湖南宁远·八年级期末)已知10个数据:0、1、1、2、2、2、3、3、3、8,其中3出现的频数是_______.
19.(2021·湖南·茶陵县教育教学研究室八年级期末)在英文单词 believe 中,字母“e”出现的频率是_______.
20.(2021·湖南永兴·八年级期末)现将一组数据:21,25,23,25,27,29,25,30,28,29,26,24,27,25,26,22,24,25,26,28分成五组,其中26.5<x<28.5的频数是____.
21.(2021·湖南隆回·八年级期末)在一串数字“1235362731”中,数字“3”出现的频率为___________.
22.(2021·湖南岳阳·八年级期末)某班50位同学中,1月份出生的频率是0.3,这个班1月份出生的同学有____人.
23.(2021·湖南湘乡·八年级期末)永州市教育部门为了了解全市中小学安全教育情况,对某校进行了“防溺水”安全知识的测试.从七年级随机抽取了50名学生的测试成绩(百分制),整理样本数据,得到下表:
成绩 90≤x≤100 80≤x<90 70≤x<80 60≤x<70 x<60
人数 25 15 5 4 1
根据抽样调查结果,估计该校七年级600名学生中,80分(含80分)以上的学生有________人.
24.(2021·湖南绥宁·八年级期末)如图是某市晚报记者在抽样调查了一些市民用于读书、读报、参加“全民健身运动”等休闲娱乐活动的时间后,绘制的频数分布直方图(共六组),已知从左往右前五组的频率之和为0.94,如果第六组有12个数,则此次抽样的样本容量是_____
25.(2021·湖南洪江·八年级期末)一个容量为80的样本最大值为143,最小值为50,取组距为10,则可以分成________组.
26.(2021·湖南炎陵·八年级期末)统计得到的一组数据的最大值为218,最小值为100,取组距为15,可分成________组.
三、解答题
27.(2021·湖南雨花·八年级期末)某学校开展了防疫知识的宣传教育活动.为了解这次活动的效果,学校从全校1500名学生中随机抽取部分学生进行知识测试(测试满分100分,得分x均为不小于60的整数),并将测试成绩分为四个等第:基本合格(60≤x<70),合格(70≤x<80),良好(80≤x<90),优秀(90≤x≤100),制作了如图统计图(部分信息未给出).
由图中给出的信息解答下列问题:
(1)求测试成绩为合格的学生人数,并补全频数直方图.
(2)求扇形统计图中“良好”所对应的扇形圆心角的度数.
(3)这次测试成绩的中位数是什么等第?
(4)如果全校学生都参加测试,请你根据抽样测试的结果,估计该校获得优秀的学生有多少人?
28.(2021·湖南武陵·八年级期末)2020年,新型冠状病毒肆虐全球,疫情期间学生在家进行网课学习和锻炼,学习和身体健康状况都有一定的影响.为了解学生身体健康状况,某校对学生进行立定跳远水平测试.随机抽取50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组 频数
a
12
b
10
学生立定跳远测试成绩的频数分布直方图
请根据图表中所提供的信息,完成下列问题:
(1)表中________,________;
(2)样本成绩的中位数落在________范围内;
(3)请把频数分布直方图补充完整;
(4)该校共有1200名学生,估计该学校学生立定跳远成绩在范围内的有多少人?
29.(2021·湖南洪江·八年级期末)为了提高学生书写汉字的能力,增强保护汉子的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为(分),且,将其按分数段分为五组,绘制出以下不完整表格:
组别 成绩(分) 频数(人数) 频率
一 2 0.04
二 10 0.2
三 14 b
四 a 0.32
五 8 0.16
请根据表格提供的信息,解答以下问题:
(1)本次决赛共有 名学生参加;
(2)直接写出表中a= ,b= ;
(3)请补全下面相应的频数分布直方图;
(4)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 .
30.(2021·湖南醴陵·八年级期末)某校为了解七年级学生的体重情况,随机抽取了七年级m名学生进行调查,将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图.
组别 体重(千克) 人数
A 37.5≤x<42.5 10
B 42.5≤x<47.5 n
C 47.5≤x<52.5 40
D 52.5≤x<57.5 20
E 57.5≤x<62.5 10
请根据图表信息回答下列问题:
(1)填空:①m=_____,②n=_____,③在扇形统计图中,C组所在扇形的圆心角的度数等于_______度;
(2)若把每组中各个体重值用这组数据的中间值代替(例如:A组数据中间值为40千克),则被调查学生的平均体重是多少千克?
(3)如果该校七年级有1000名学生,请估算七年级体重低于47.5千克的学生大约有多少人?
31.(2021·湖南新化·八年级期末)九(1)班同学为了解2011年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量(t) 频数(户) 频率
6 0.12
0.24
16 0.32
10 0.20
4
2 0.04
请解答以下问题:
(1)把上面的频数分布表和频数分布直方图补充完整;
(2)若该小区用水量不超过15t的家庭占被调查家庭总数的百分比;
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
32.(2021·湖南临湘·八年级期末)为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了“汉字听写大赛”.经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,写错或不写不得分.根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下图表:
组别 成绩x分 频数(人数)
第1组 25≤x<30 4
第2组 30≤x<35 8
第3组 35≤x<40 16
第4组 40≤x<45 a
第5组 45≤x<50 10
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
33.(2021·湖南长沙·八年级期末)今年受疫情影响,我市中小学生全体在家线上学习.为了了解学生在家主动锻炼身体的情况,某校随机抽查了部分学生,对他们每天的运动时间进行调查,并将调查统计的结果分为四类:每天运动时间t≤20分钟的学生记为A类,20分钟<t≤40分钟记为B类,40分钟<t≤60分钟记为C类,t>60分钟记为D类.收集的数据绘制如下两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
(1)这次共抽取了_________名学生进行调查统计;
(2)扇形统计图中D类所对应的扇形圆心角大小为_________;
(3)将条形统计图补充完整;
(4)如果该校共有1500名学生,请你估计该校B类学生约有多少人?
34.(2021·湖南宁远·八年级期末)某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x<100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
分数段 频数 频率
60≤x<70 18 0.36
70≤x<80 17 c
80≤x<90 a 0.24
90≤x<100 b 0.06
合计 1
根据以上信息解答下列问题:
(1)统计表中c的值为________;样本成绩的中位数落在分数段________中;
(2)补全频数直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评的作品数量是多少.
35.(2021·湖南双峰·八年级期末) 某校为加强学生安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分100分)进行统计,请根据尚为完成的频率和频数分布直方图,解答下列问题:
分数段 频数 频率
50.5~60.5 16 0.08
60.5~70.5 40 0.2
70.5~80.5 50 0.25
80.5~90.5 m 0.35
90.5~100.5 24 n
(1)这次抽取了______名学生的竞赛成绩进行统计,其中m=______,n=______;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
36.(2021·湖南鹤城·八年级期末)“新型冠状病毒肺炎”疫情牵动着亿万国人的心,为进一步加强疫情防控工作,某学校利用网络平台进行疫情防控知识测试.小青从全体学生中随机抽取部分同学的分数(得分取正整数,满分为100分)进行统计,以下是根据抽取同学的分数制作的不完整的频率分布表和频率分布直方图,请根据图表,回答下列问题:
组别 分组 频数 频率
1 9 0.18
2
3 21 0.42
4 0.06
5 2
(1)根据上表填空:a= ,b= ,m= ;
(2)若小青的测试成绩是抽取的同学成绩的中位数,则小青的测试成绩在什么范围内?
(3)若规定:得分在90≤x≤100的为“优秀”,若小青所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加决赛,请问共有多少名学生被选拔参加决赛?
37.(2021·湖南绥宁·八年级期末)垃圾分类是一项“利国利民”的民生工程,需要全社会的共同参与.某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾,如图表是七年级各班一周收集的可回收垃圾的重量(千克)的频数表和频数分布直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的重量的频数表
组别(kg) 频数
4.0~4.5 2
4.5~5.0 a
5.0~5.5 3
5.5~6.0 1
(1)求a的值
(2)已知收集的可回收垃圾以1.1元/kg被回收,该年级这周收集的可回收垃圾被回收后所得金额能否达到60元?
38.(2021·湖南永兴·八年级期末)某班学生的期中成绩(成绩为整数)的频数分布表如下,请根据表中提供的信息回答下列问题:
分组 频数 频率
49.5<x<59.5 2 0.04
59.5<x<69.5 6 m
69.5<x<79.5 n 0.44
79.5<x<89.5 15 0.3
89.5<x<99.5 5 p
合计 q 1.0
(1)m= ,n= ,p= ,q= ;
(2)在表内,频率最小的一组的成绩范围是 ;
(3)成绩优秀的学生有 人(成绩大于或等于80分为优秀).
(4)你认为该班学生的学习成绩怎么样?根据数据说明你的看法.
试卷第1页,共3页
参考答案:
1.D
【分析】
用不超过15分钟的通话时间除以所有的通话时间即可求得通话时间不超过15分钟的频率.
【详解】
解:∵不超过15分钟的通话次数为20+16+9=45次,通话总次数为20+16+9+5=50次,
∴通话时间不超过15min的频率为=0.9,
故选D.
【点睛】
本题考查了频数分布表的知识,解题的关键是了解频率=频数÷样本容量,难度不大.
2.C
【分析】
先求得第5组的频数,再除以总学生数即可.
【详解】
由第5组频数为:,得第五组的频率为.
故选:C.
【点睛】
此题考查频数与频率的关系,知道所有频数之和为样本容量及每组频率等于其频数与样本容量的商是关键.
3.C
【分析】
根据频率的计算方法判断各个选项.
【详解】
解:A、应为:出现正面的频数是4,错误,不符合题意;
B、应为:出现反面的频数是6,错误,不符合题意;
C、正确,符合题意;
D、出现正面的频率是40%,错误,不符合题意.
故选:C.
【点睛】
本题考查了频率以及频数的概念,熟知频率的计算方法是解本题的关键.
4.D
【详解】
试题分析:频率等于频数除以数据总和,∵小明共投篮80次,进了50个球,∴小明进球的频率=50÷80=0.625,故选D.
考点:频数与频率.
5.B
【详解】
跳绳次数在90~110之间的数据有91,93,100,102四个,故频率为 =0.2.
故选B.
6.C
【分析】
根据频率公式:频率=频数÷总数即可求解.
【详解】
解:根据题意,得=0.2,
解得m=50.
故选:C.
【点睛】
本题考查了频率的计算公式,理解公式是解题的关键.
7.A
【分析】
先求出该组的频数,再利用频率计算公式求出答案.
【详解】
解:第④组的频数是100-14-11-12-15-13-12-10=13,
∴第④组的频率是,
故选:A.
【点睛】
此题考查频率的计算公式:频数除以总数,熟记公式是解题的关键.
8.B
【分析】
根据频率=求解即可.
【详解】
解:由题意可知,共反馈10种结果,其中A出现3次,
∴A类粽子出现次数的频率是
故选:B
【点睛】
本题考查频率的概念,掌握频率=是本题的解题关键.
9.D
【分析】
根据频率=“正面朝上的频数”÷投掷硬币的总数,即可解答.
【详解】
解:∵小明投掷一枚硬币100次,出现“正面朝上”51次,
∴“正面朝上”的频率为:,
故选:D.
【点睛】
本题考查了频率的定义,熟知定义是解题的关键.
10.D
【分析】
根据频率直方图可以知道被调查的总人数,又在要求的范围可以很直观地由图形看出,即可得出百分比.
【详解】
解:由频率直方图可以得出,被调查的总人数=3+10+12+5=30.
又仰卧起坐次数在25~30次的学生人数为12,故百分比为40%,
故选D.
【点睛】
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
11.C
【详解】
试题分析:根据图形所给出的数据可得:
∵15﹣20元的有20人,人数最多,∴捐款人数最多的一组是15﹣20元.
故选C.
考点:频数分布直方图.
12.C
【分析】
根据直方图表示的意义求得统计的总人数,以及每组的人数即可判断.
【详解】
解:①小文同学一共统计了4+8+14+20+16+12=74(人),故①说法错误,不符合题意;
②每天微信阅读不足20分钟的人数有4+8=12(人),故②说法正确,符合题意;
③每天微信阅读30﹣40分钟的人数最多,故③说法正确,符合题意;
④每天微信阅读0﹣10分钟的人数最少,故④说法正确,符合题意.
故选:C.
【点睛】
本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
13.8
【分析】
直接用尺码L的频率乘以班级总人数即可求出答案.
【详解】
解:由表可知尺码L的频率的0.2,又因为班级总人数为40,
所以该班学生所穿校服尺码为“L”的人数有400.2=8.
故答案是:8.
【点睛】
此题主要考查了频数与频率,关键是掌握频数是指每个对象出现的次数.频率是指每个对象出现的次数与总次数的比值(或者百分比).即频率=频数÷总数.
14.4
【分析】
首先根据频率的计算公式求得第五组的频数,然后利用总数减去其它组的频数即可求解.
【详解】
第五组的频数是40×0.2=8,
则第六组的频数是40-5-10-6-7-8=4.
故答案是:4.
【点睛】
本题是对频率、频数灵活运用的综合考查.
注意:每个小组的频数等于数据总数减去其余小组的频数,即各小组频数之和等于数据总和.
15.0.0625
【分析】
利用频率与频数的关系得出第1组到第4组的频率,进而得出第8组的频率.
【详解】
解:∵把容量是64的样本分成8组,从第1组到第4组的频数分别是5,7,11,13,
∴第1组到第4组的频率是:(5+7+11+13)0.5625
∵第5组到第7组的频率是0.125,
第8组的频率是:1- 0.5625-0.125= 0.0625
故答案为: 0.0625.
【点睛】
此题主要考查了频数与频率,正确求出第5组到第7组的频数是解题关键.
16.6
【分析】
根据各小组的频率之和等于1,即可得出第一组与第二组的频率和,然后求出数据总数,从而求出m的值.
【详解】
解:∵第一组与第二组的频率之和为1-30%=70%,
∴该班男生的总人数为(6+8)÷70%=20,
∴m= 20×30%=6.
故答案为:6.
【点睛】
本题主要考查了频数与频率,频率是指每个对象出现的次数与总次数的比值(或者百分比),即频率=频数÷总数.
17.20
【分析】
根据频率的计算公式即可得到答案.
【详解】
解:
所以可得参加比赛的人数为20人.
故答案为20.
【点睛】
本题主要考查频率的计算公式,这是数据统计的重点知识,必须掌握.
18.3.
【分析】
直接利用频数的定义分析得出答案.
【详解】
解:10个数据:0、1、1、2、2、2、3、3、3、8,其中3出现了3次,故3出现的频数是3.
故答案为3.
【点睛】
本题主要考查了频数的定义,正确把握频数的定义是解题的关键.
19.
【分析】
先求出英文单词believe总的字母个数和e的个数,再根据握频率=进行计算即可.
【详解】
∵英文单词believe共有7个字母,其中有3个e,
∴字母“e”出现的频率是;
故答案为:.
【点睛】
此题考查频数与频率,解题关键在于掌握频率的计算公式即可.
20.4
【分析】
先将各数据划记到对应的小组,再正确数出第四组26.5~28.5的频数即可.
【详解】
解:这组数据中26.5<x<28.5的数据,即是数据27、28出现的次数,
通过统计数据27、28共出现4次,
故答案为:4.
【点睛】
本题考查频率、频数的概念,一般称落在不同小组中的数据个数为该组的频数,频数与数据总数的比值为频率.
21.
【分析】
根据频率=频数÷总数求解即可得到答案.
【详解】
解:∵在一串数字“1235362731”中,数字“3”出现的次数为3次,数字数目为10,
∴数字“3”出现的频率,
故答案为:.
【点睛】
本题主要考查了频率的计算,解题的关键在于能够熟记频率=频数÷总数.
22.15
【分析】
根据频率的求法,频率=频数÷数据总和,计算可得答案.
【详解】
解:50×0.3=15人,
故答案为:15.
【点睛】
本题主要考查了频率的计算公式,是需要识记的内容.
23.480
【分析】
用七年级的学生总数乘以样本中80分以上的比例即可得到答案.
【详解】
600×=480(人)
故答案为:480.
【点睛】
本题考查了频数分布图、用样本估计总体,解答本题的关键是明确题意,由样本数据可以估计总体;
24.200
【分析】
根据频数分布直方图中各组的频率总和等于1,计算可得第六组的频率,根据第六组的频数,进而根据频率的计算公式计算可得答案.
【详解】
解:根据频数分布直方图中每一组内的频率总和等于1,可知第六组的频率为1﹣0.94=0.06,又因为第六组有12个数,所以此次抽样的样本容量是12÷0.06=200.
故答案为:200.
【点睛】
本题考查了读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
25.10
【分析】
根据组距,最大值、最小值、组数以及样本容量的关系进行计算即可.
【详解】
解:(143-50)÷10=9.3≈10,
故可以分成10组
故答案为:10.
【点睛】
本题考查频数分布直方图的制作方法,理解组距、组数,极差以及样本容量之间的关系是正确解答的关键.
26.
【分析】
根据组数=(最大值-最小值)÷组距计算,注意小数部分要进位.
【详解】
解:在样本数据中最大值为218,最小值为100,它们的差是218-100=118,
已知组距为15,由于118÷15, 故可以分成8组.
故答案为:8.
【点睛】
本题考查的是组数的计算,数据分成的组的个数称为组数是解题的关键,注意小数部分要进位.
27.(1)见解析;(2)144°;(3)这次测试成绩的中位数的等第是良好;(4)估计该校获得优秀的学生有300人
【分析】
(1)根据基本合格人数已经百分比求出总人数即可解决问题;
(2)根据圆心角=360°×百分比计算即可;
(3)根据中位数的定义判断即可;
(4)利用样本估计总体的思想解决问题即可.
【详解】
解:(1)30÷15%=200(人),
200﹣30﹣80﹣40=50(人),
直方图如图所示:
;
(2)“良好”所对应的扇形圆心角的度数=360°×=144°;
(3)这次成绩按从小到大的顺序排列,中位数在80分-90分之间,
∴这次测试成绩的中位数的等第是良好;
(4)1500×=300(人),
答:估计该校获得优秀的学生有300人.
【点睛】
本题考查频数分布直方图,样本估计总体,扇形统计图,中位数等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
28.(1),;(2);(3)详见解析;(4)240人
【分析】
(1)根据频数分布直方图可以求得a的值,再根据样本容量求出b的值.
(2)结合中位数的求法可以求出中位数落在哪一组.
(3)根据(1)中的结果可以将频数分布直方图补充完整.
(4)根据频数分步表中的数据可以求出该学校学生立定跳远成绩在范围内的有多少人.
【详解】
解(1)由统计图可得,;
(2)有50名学生进行测试,第25和26名的成绩和的平均数为中位数
样本成绩的中位数落在范围内;
(3)由(1)知,,补全的频数分布直方图如右图所示;
学生立定跳远测试成绩的频数分布直方图
(4)(人),
答:估计该学校学生立定跳远成绩在范围内有240人.
【点睛】
本题考查频数分步表、频数分步直方图、中位数、用样本估计总体,解答本题的关键是明确题意,利用数形结合思想解答.
29.(1)50;(2)a=16,b=0.28;(3)答案见解析;(4)48%.
【详解】
试题分析:(1)根据第一组别的人数和百分比得出样本容量;(2)根据样本容量以及频数、频率之间的关系得出a和b的值,(3)根据a的值将图形补全;(4)根据图示可得:优秀的人为第四和第五组的人,将两组的频数相加乘以100%得出答案.
试题解析:(1)2÷0.04=50
(2)50×0.32=16 14÷50=0.28
(3)
(4)(0.32+0.16)×100%=48%
考点:频数分布直方图
30.(1)①100,②20,③144;(2)被被抽取同学的平均体重为50千克;(3)七年级学生体重低于47.5千克的学生大约有300人.
【分析】
(1)①m=20÷20%=100,②n=100-10-40-20-10=20,③c=×360°=144°;
(2)被抽取同学的平均体重为:
.(千克);
(3)七年级学生体重低于47.5千克的学生1000×30%=300(人).
【详解】
(1)①100,②20,③144;
(2)被抽取同学的平均体重为:
.
答:被抽取同学的平均体重为50千克.
(3).
答:七年级学生体重低于47.5千克的学生大约有300人.
【点睛】
本题考查的是频数分布表和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.频数分布表能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
31.(1)见解析
(2)该小区用水量不超过15t的家庭占被调查家庭总数的百分比为68﹪.
(3)该小区月均用水量超过20t的家庭大约有120户.
【分析】
频数(率)分布表,频数分布直方图,频数、频率和总量的关系,用样本估计总体.
(1)根据0<x≤5中频数为6,频率为0.12,则调查总户数为6÷0.12=50,进而得出在5<x≤10范围内的频数以及在20<x≤25范围内的频率.
(2)根据(1)中所求即可得出不超过15t的家庭总数即可求出,不超过15t的家庭占被调查家庭总数的百分比.
(3)根据样本数据中超过20t的家庭数,即可得出1000户家庭超过20t的约家庭数.
【详解】
解:(1)如图所示:
根据0<x≤5中频数为6,频率为0.12,则6÷0.12=50,
∴月均用水量5<x≤10的频数:50×0.24=12户;
月均用水量20<x≤25的频率:4÷50=0.08.
∴统计中的频数分布表和不完整的频数分布直方图,补充如下;
月均用水量(t) 频数(户) 频率
6 0.12
12 0.24
16 0.32
10 0.20
4 0.08
2 0.04
(2)用水量不超过15吨是前三组,
∴该小区用水量不超过15t的家庭占被调查家庭总数的百分比为
(0.12+0.24+0.32)×100﹪=68﹪.
(3)用水量超过20t是最后两组,
∴该小区月均用水量超过20t的家庭大约有:1000×(0.04+0.08)=120(户).
32.(1)a=12;(2)补图见解析;(3)本次测试的优秀率是44%.
【分析】
(1)用总数50减去其他各组的频数即可求得a的值;
(2)由(1)的结果即可把频数分布直方图补充完整;
(3)由百分比的意义即可求解.
【详解】
(1)a=50﹣4﹣8﹣14﹣10=12;
(2)如图所示:
(3)本次测试的优秀率是:(12+10)÷50×100%=44%.
33.(1)50;(2)36°;(3)图见解析;(4)该校B类学生约有660人.
【分析】
(1)根据A类的条形统计图和扇形统计图信息即可得;
(2)先根据题(1)的结论求出D类学生的人数,再求出D类学生的人数占比,然后乘以360°可得圆心角的大小;
(3)由(2)即可得补充条形统计图;
(4)先求出B类学生的人数占比,再乘以1500即可得.
【详解】
(1)这次调查共抽取的学生人数为15÷30%=50(名)
故答案为:50;
(2)D类学生的人数为50 15 22 8=5(名)
则D类学生的人数占比为×100%=10%
D类所对应的扇形圆心角大小为360°×10%=36°
(3)条形统计图补全如下:
(4)B类学生的人数占比为×100%=44%
则1500×44%=660(人)
答:该校B类学生约有660人.
【点睛】
本题考查了条形统计图和扇形统计图的信息关联、画条形统计图等知识点,熟练掌握统计调查的相关知识是解题关键.
34.(1)0.34;70≤x<80;(2)见解析;(3) 180幅.
【分析】
(1)由60≤x<70频数和频率求得总数,根据频率=频数÷总数求得a、b、c的值,由中位数定义求解可得;
(2)根据(1)中所求数据补全图形即可得;
(3)总数乘以80分以上的频率即可.
【详解】
解:(1)本次调查的作品总数为18÷0.36=50(幅),
则c=17÷50=0.34,a=50×0.24=12,b=50×0.06=3,
其中位数为第25、26个数的平均数,
∴中位数落在70≤x<80中,
故答案为0.34,70≤x<80;
(2)补全图形如下:
(3)600×(0.24+0.06)=180(幅),
答:估计全校被展评作品数量是180幅.
【点睛】
本题考查读频数(率)分布直方图的能力和利用统计图获取信息的能力,以及条形统计图;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
35.(1)200,70,0.12;(2)详见解析;(3)420
【分析】
(1)根据50.5~60.5的频数和频率先求出总数,再根据频数、频率和总数之间的关系分别求出m、n的值;
(2)根据(1)的结果可补全统计图;
(3)用全校的总人数乘以成绩在70分以下(含70分)的学生所占的百分比,即可得出答案.
【详解】
解:(1)根据题意得:=200(名),
m=200×0.35=70(名),
n==0.12;
故答案为:200,70,0.12;
(2)根据(1)补图如下:
(3)根据题意得:
1500×(0.08+0.2)=420(人),
答:该校安全意识不强的学生约有420人.
【点睛】
此题主要考查了频数分布直方图、频数分布表、利用样本估计总体,关键是读懂频数分布直方图,能利用统计图获取信息;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
36.(1)3,0.3,15,(2);(3)共有24名学生被选拔参加决赛.
【分析】
(1)根据频数、频率、总数之间的关系一一解决问题即可;
(2)根据中位数的定义即可判断;
(3)用样本估计总体的思想解决问题即可.
【详解】
解:(1)(人.
,,.
故答案为:3,0.3,15
(2)抽取的学生共有50名,中位数是第25、26个数据的平均数,第25、26个数据在第3组,所以小青的测试成绩在范围内;
(3)(人)
答:共有24名学生被选拔参加决赛.
【点睛】
本题考查频数分布直方图、频数分布表、中位数的定义等知识,解题的关键是熟练掌握基本知识.
37.(1)a=4;(2)不能达到
【分析】
(1)由频数分布直方图可得4.5~5.0的频数a的值;
(2)先求出该年级这周收集的可回收垃圾的质量的最大值,再乘以单价即可得出答案.
【详解】
解:(1)由频数分布直方图可知4.5~5.0的频数a=4;
(2)∵该年级这周收集的可回收垃圾的质量小于4.5×2+5.0×4+5.5×3+6.0=51.5(kg),
∴该年级这周收集的可回收垃圾被回收后所得金额小于51.5×1.1=56.65(元),
∴该年级这周收集的可回收垃圾被回收后所得金额不能达到60元.
【点睛】
本题主要考查了频数分布表,频数分布直方图,解题的关键在于能够准确读懂题意.
38.(1)0.12,22,0.1,50;(2)49.5<x<59.5;(3)20;(4)见解析
【分析】
(1)先根据49.5<x<59.5的频数及其频率求解可得样本容量q的值,再根据频率=频数÷样本容量和频数=样本容量×频率求解即可;
(2)根据以上所求结果即可得出答案;
(3)将79.5<x<89.5、89.5<x<99.5的频数相加即可;
(4)答案不唯一,合理均可.
【详解】
解:(1)∵q=2÷0.04=50,
∴m=6÷50=0.12,
n=50×0.44=22,
p=5÷50=0.1,
故答案为:0.12、22、0.1、50;
(2)在表内,频率最小的一组的成绩范围是49.5<x<59.5,
故答案为:49.5<x<59.5;
(3)成绩优秀的学生人数为15+5=20(人),
故答案为:20;
(4)成绩很好,
理由:优秀人数多,有20人(答案不唯一).
【点睛】
本题主要考查了频数分布表,在统计数据时,经常把数据按照不同的范围分成几个组,分成的组的个数称为组数,每一组两个端点的差称为组距,称这样画出的统计图表为频数分布表.
答案第1页,共2页
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
