1.3带电粒子在有界磁场中的运动 课件(共60张PPT) 人教版(2019)选择性必修第二册
文档属性
| 名称 | 1.3带电粒子在有界磁场中的运动 课件(共60张PPT) 人教版(2019)选择性必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 906.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-26 21:58:36 | ||
图片预览






文档简介
(共60张PPT)
1.3带电粒子在磁场中运动
1.带电粒子在匀强磁场中
运动( ),只受洛伦兹
力作用,做 .
简单回顾
2.洛伦兹力提供向心力:
半径:
带电粒子在匀强磁场中的运动规律
周期:
匀速圆周运动
o
v
F
-
一.两个公式:
V
V
V
V
带电粒子做圆周运动的分析方法
V
V
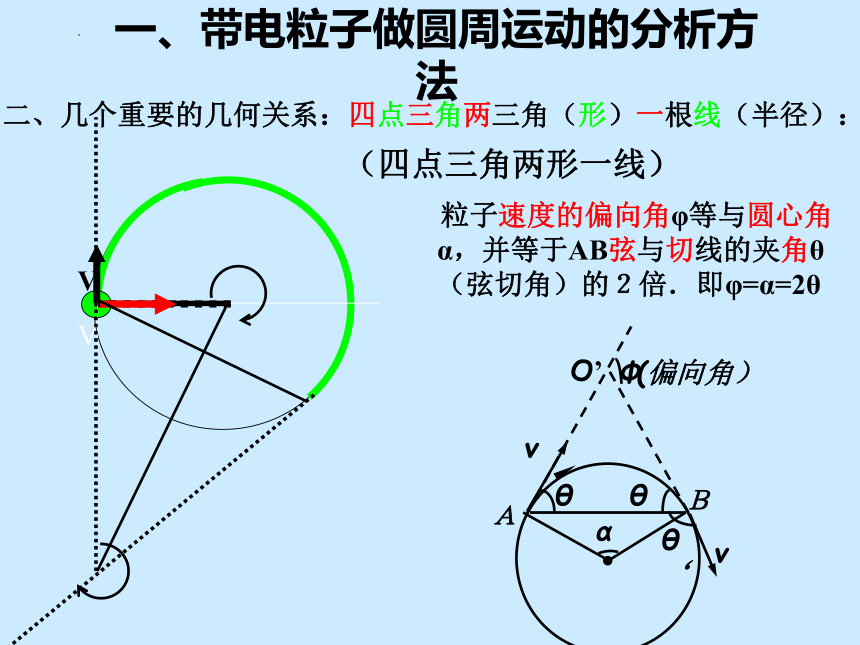
一、带电粒子做圆周运动的分析方法
二、几个重要的几何关系:四点三角两三角(形)一根线(半径):
A
v
v
O’
α
B
θ
θ
θ‘
Φ(偏向角)
粒子速度的偏向角φ等与圆心角α,并等于AB弦与切线的夹角θ(弦切角)的2倍.即φ=α=2θ
(四点三角两形一线)
带电粒子做圆周运动的分析方法
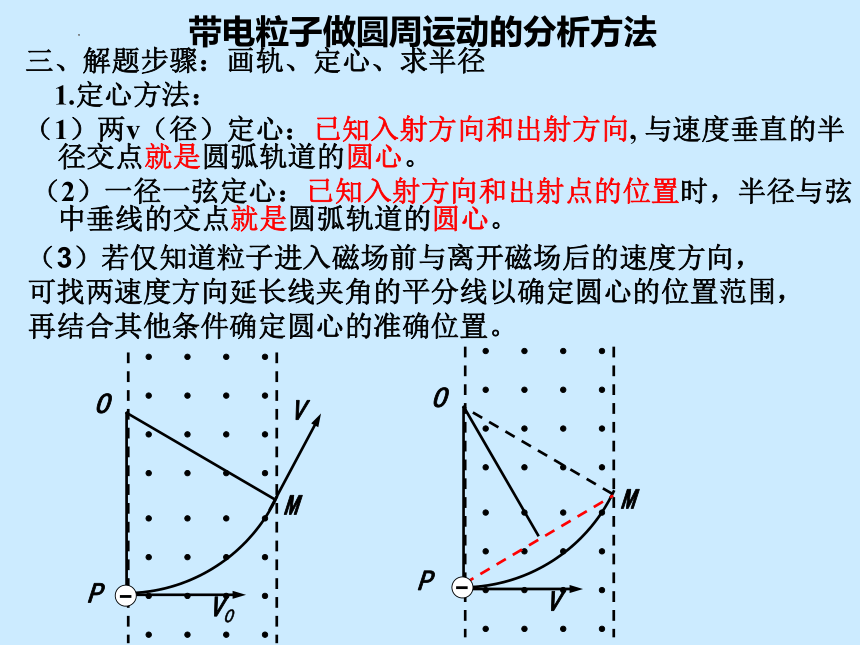
三、解题步骤:画轨、定心、求半径
1.定心方法:
(1)两v(径)定心:已知入射方向和出射方向, 与速度垂直的半径交点就是圆弧轨道的圆心。
(2)一径一弦定心:已知入射方向和出射点的位置时,半径与弦中垂线的交点就是圆弧轨道的圆心。
V
P
M
O
V0
P
M
O
V
(3)若仅知道粒子进入磁场前与离开磁场后的速度方向,
可找两速度方向延长线夹角的平分线以确定圆心的位置范围,
再结合其他条件确定圆心的准确位置。
带电粒子做圆周运动的分析方法
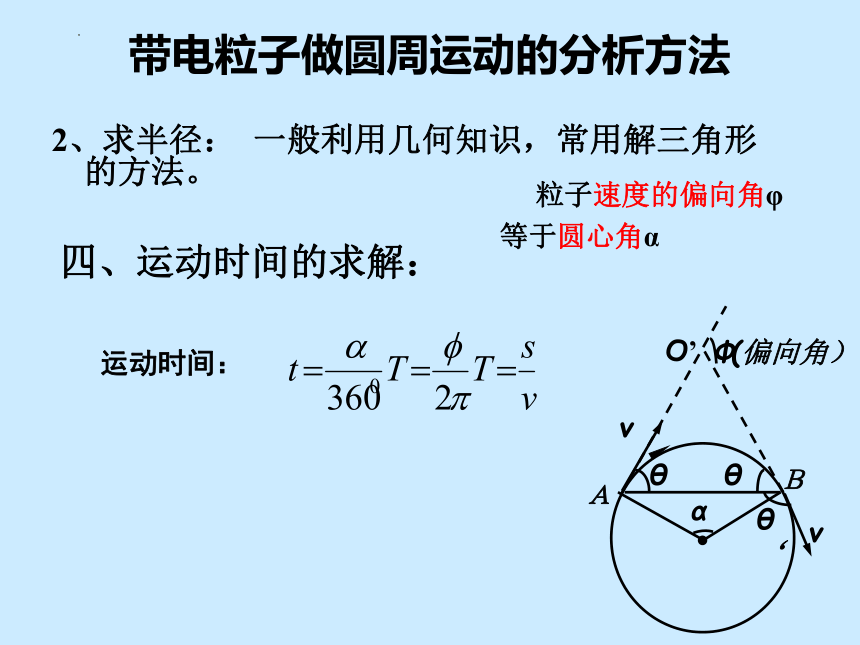
2、求半径: 一般利用几何知识,常用解三角形的方法。
运动时间:
四、运动时间的求解:
A
v
v
O’
α
B
θ
θ
θ‘
Φ(偏向角)
粒子速度的偏向角φ
等于圆心角α
五、关注三类典型问题
1.带电粒子在有界磁场中做圆弧运动;
2.带电粒子在磁场中运动时的一些临界问题的讨论
3.多解问题
带电粒子在磁场中运动
v
v
v
v
v
v
v
v
v
v
v
v
v
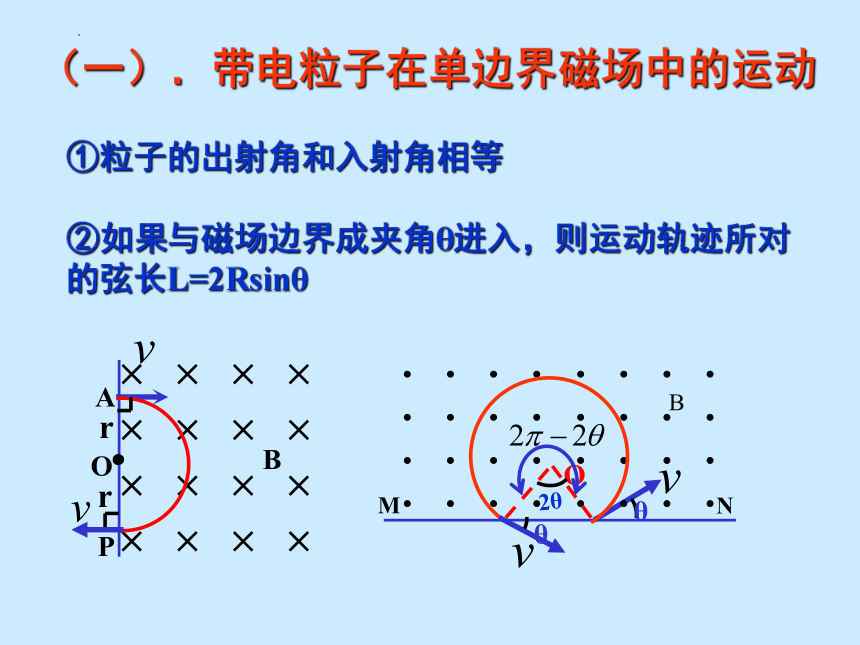
(一).带电粒子在单边界磁场中的运动
①粒子的出射角和入射角相等
②如果与磁场边界成夹角θ进入,则运动轨迹所对的弦长L=2Rsinθ
O
B
A
.
r
r
P
θ
M
N
B
O
2θ
θ
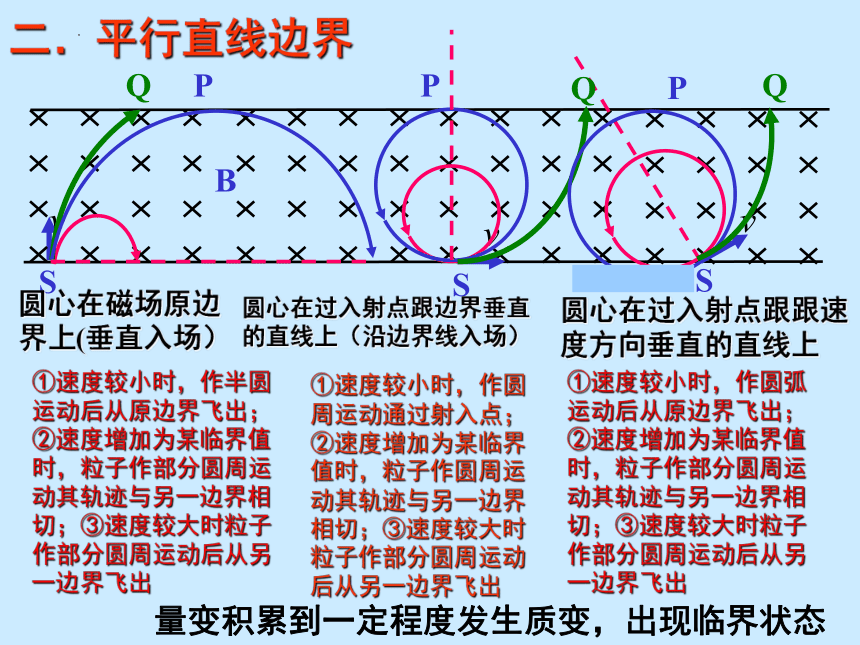
二.平行直线边界
①速度较小时,作半圆运动后从原边界飞出;②速度增加为某临界值时,粒子作部分圆周运动其轨迹与另一边界相切;③速度较大时粒子作部分圆周运动后从另一边界飞出
S
B
P
S
S
Q
P
Q
Q
①速度较小时,作圆周运动通过射入点;②速度增加为某临界值时,粒子作圆周运动其轨迹与另一边界相切;③速度较大时粒子作部分圆周运动后从另一边界飞出
圆心在过入射点跟跟速度方向垂直的直线上
圆心在过入射点跟边界垂直的直线上(沿边界线入场)
圆心在磁场原边界上(垂直入场)
量变积累到一定程度发生质变,出现临界状态
P
①速度较小时,作圆弧运动后从原边界飞出;②速度增加为某临界值时,粒子作部分圆周运动其轨迹与另一边界相切;③速度较大时粒子作部分圆周运动后从另一边界飞出
三、垂直边界
例. 一个质量为m电荷量为q的带电粒子从x轴上的P(a,0)点以速度v,沿与x正方向成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴射出第一象限。求:
(1)匀强磁场的磁感应强度B和射出点的坐标。
(2)带电粒子在磁场中的运动时间是多少?
y
x
o
B
v
v
a
O/
解:(1)
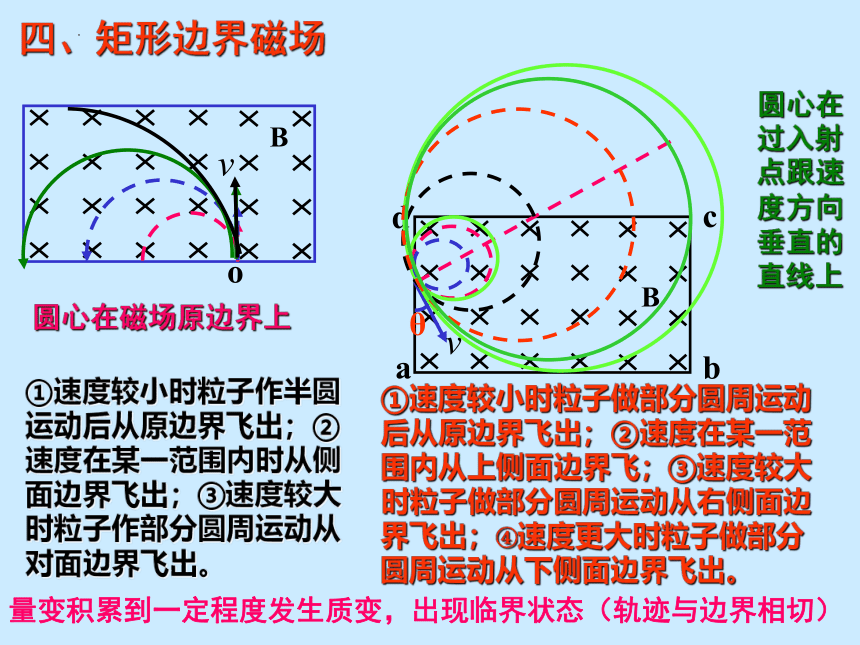
四、矩形边界磁场
o
B
d
a
b
c
θ
B
圆心在磁场原边界上
圆心在过入射点跟速度方向垂直的直线上
①速度较小时粒子作半圆运动后从原边界飞出;②速度在某一范围内时从侧面边界飞出;③速度较大时粒子作部分圆周运动从对面边界飞出。
①速度较小时粒子做部分圆周运动后从原边界飞出;②速度在某一范围内从上侧面边界飞;③速度较大时粒子做部分圆周运动从右侧面边界飞出;④速度更大时粒子做部分圆周运动从下侧面边界飞出。
量变积累到一定程度发生质变,出现临界状态(轨迹与边界相切)
究竟从哪个边先出还要看边界的长宽
V0
O
a
b
c
d
θ
300
600
●
●
五.圆形边界
B
θ
θ
O’
O
入射速度方向指向匀强磁场区域圆的圆心,刚出射时速度方向的反向延长线必过该区域圆的圆心.
径向入、径向出
O1
O2
O3
O4
r v
R
v
O/
O
五.圆形边界
B
θ
O’
O
θ
B
θ
θ
O’
O
径向入、径向出
偏心入、偏心出
例.如图14所示,边长为L的等边三角形ABC为两个有界匀强磁场的理想边界,三角形内的磁场方向垂直纸面向外,磁感应强度大小为B,三角形外的磁场(足够大)方向垂直纸面向里,磁感应强度大小也为B.把粒子源放在顶点A处,它将沿∠A的角平分线发射质量为m、电荷量为q、初速度为v= 的负电粒子(粒子重力不计).求:
图14
(1)从A射出的粒子第一次到达C点所用时间为多少
(2)带电粒子在题设的两个有界磁场中运动的周期.
六、三角形磁场
解析 (1)带电粒子垂直进入磁场,做匀速圆周运动
qvB=
T=
将已知条件代入有r =L
从A点到达C点的运动轨
迹如图所示,可得
tAC= T
tAC=
(2)带电粒子在一个运动的周期运动轨迹如第(1)问图所示.
粒子通过圆弧从C点运动至B点的时间为
tCB=
带电粒子运动的周期为TABC=3(tAC+tCB)
解得TABC=
答案 (1) (2)
七.环形边界
r1
O
O2
例1、如图直线MN上方有磁感应强度为B的匀强磁场。正、负电子同时从同一点O以与MN成30 角的同样速度v射入磁场(电子质量为m,电荷为e),它们从磁场中射出时相距多远?射出的时间差是多少?
M
N
B
O
v
例2、一带电质点,质量为m,电量为q,以平行于x轴的速度v从y轴上的a点射入图中第一象限所示的区域,为了使该质点能从x轴上的b点以垂直于x轴的速度v射出,可在适当的地方加一个垂直于xy平面、磁感强度为B的匀强磁场。若此磁场仅分布在一个圆形区域内,试求这圆形磁场区域的最小半径。重力忽略不计
例3、如图,在一水平放置的平板MN上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向里,许多质量为m,带电量为+q的粒子,以相同的速率v沿位于纸面内的各个方向,由小孔O射入磁场区域,不计重力,不计粒子间的相互影响。下列图中阴影部分表示带电粒子可能经过的区域,其中R=mv/qB。哪个图是正确的 ( )
2R
R
2R
M
N
O
2R
R
2R
M
N
O
2R
2R
2R
M
N
O
R
2R
2R
M
N
O
D.
A.
B.
C.
A
M
N
B
O
B
M
B
O
v
……以速率 v 沿纸面各个方向由小孔O射入磁场
B
v
F
B
v
F
B
v
2R
R
2R
M
N
O
解:带电量为+q的粒子,以相同的速率v沿位于纸面内的各个方向,由小孔 O 射入磁场区域,由R=mv/qB,各个粒子在磁场中运动的半径均相同,
在磁场中运动的轨迹圆圆心是在以O为圆心、以R=mv/qB为半径的1/2圆弧上,如图虚线示:
各粒子的运动轨迹如图实线示:
带电粒子可能经过的区域阴影部分如图斜线示
例4、核聚变反应需要几百万度以上的高温,为把高温条件下高速运动的离子约束在小范围内(否则不可能发生核反应),通常采用磁约束的方法(托卡马克装置)。如图所示,环状匀强磁场围成中空区域,中空区域中的带电粒子只要速度不是很大,都不会穿出磁场的外边缘而被约束在该区域内。设环状磁场的内半径为R1=0.5m,外半径R2=1.0m,磁场的磁感强度B=1.0T,若被束缚带电粒子的荷质比为q/m=4×107C/㎏,中空区域内带电粒子具有各个方向的速度。试计算
(1)粒子沿环状的半径方向射入磁场,不能穿越磁场的最大速度。
(2)所有粒子不能穿越磁场的最大速度。
解析:(1)要粒子沿环状的半径方向射入磁场,不能穿越磁场,则粒子的临界轨迹必须要与外圆相切,轨迹如图所示。
由图中知,
解得
由
得
r1
所以粒子沿环状的半径方向射入磁场,不能穿越磁场的最
大速度为
O
O2
(2)当粒子以V2的速度沿与内圆相切方向射入磁场且轨道与外圆相切时,则以V2速度沿各方向射入磁场区的粒子都不能穿出磁场边界,如图所示。
由图中知
由 得
所以所有粒子不能穿越磁场的最大速度
带电粒子在有“圆孔”的磁场中运动
例5、在如图所示的平面直角坐标系xoy中,有一个圆形区域的匀强磁场(图中未画出),磁场方向垂直于xoy平面,O点为该圆形区域边界上的一点。现有一质量为m,带电量为+q的带电粒子(重力不计)从O点以初速度vo沿+x方向进入磁场,已知粒子经过y轴上P点时速度方向与+y方向夹角为θ=30 ,OP=L 求:⑴磁感应强度的大小和方向 ⑵该圆形磁场区域的最小面积。
O
y
x
P
v0
v0
θ
L
分析: OP的垂直平分线与v0的反向延长线交于Q, 作OQ的垂直平分线与OP相交于O′, O′即带电粒子运动轨迹圆的圆心。带电粒子在磁场中所做的是1/3圆周的匀速圆周运动。
O
y
x
P
v0
v0
θ
O′
Q
不确定边界问题
O
y
x
P
v0
v0
θ
解:(1)由左手定则得磁场方向垂直xoy平面向里,粒子在磁场中所做的是1/3圆周的匀速圆周运动,如图所示,粒子在Q点飞出磁场,设其圆心为O′,半径为R,
Q
O′
L
120°
θ
(L-R)sin30°=R……… ① ∴ R=L/3
…… ②
① ②得
(2)由图得
例6 、如图所示,现有一质量为m、电量为e的电子从y轴上的P(0,a)点以初速度v0平行于x轴射出,为了使电子能够经过x轴上的Q(b,0)点,可在y轴右侧加一垂直于xOy平面向里、宽度为L的匀强磁场,磁感应强度大小为B,该磁场左、右边界与y轴平行,上、下足够宽(图中未画出)。已知,
L<b。试求磁场的左边界距坐标原点的可能距离。
(结果可用反三角函数表示)
x
y
0
Q
v0
P
解:
x
y
0
Q
v0
P
图1
设电子在磁场中作圆周运动的轨道半径为r, 则
①
解得 ②
⑴当r>L时,磁场区域及电子运动轨迹如图1所示,
θ
θ
由几何关系有 ③
则磁场左边界距坐标原点的距离为
④
(其中 ) ⑤
②当rx
y
0
Q
v0
P
图2
由几何关系得磁场左边界距坐标原点的距离为
解得 ⑦
反思总结
返回
小结
1.带电粒子进入有界磁场,运动轨迹为一段弧线.
2.当同源粒子垂直进入磁场的运动轨迹
3.注意圆周运动中的有关对称规律:
(2) 粒子进入单边磁场时,入射速度与边界夹角等于出射速度与边界的夹角;
(1) 在圆形磁场区域内,沿径向射入的粒子,必沿径向射出.
4、带电粒子在磁场中运动问题的解题思路
找圆心
画轨迹
已知两点速度方向(两径找心)
已知一点速度方向和另一点位置
(一径一弦找心)
两洛伦兹力方向的延长线交点为圆心
弦的垂直平分线与一直径的交点为圆心
v1
O
v2
A
B
v1
A
B
O
求半径
O3
r
r
O4
r
r
O2
r
r
O1
r
r
O
S
1.一朵梅花
带电粒子在磁场中运动轨迹赏析
带电粒子在复合场中运动的轨迹欣赏
r
x
y
y
2.一座“拱桥”
(重力不计)
O1
O2
O3
L
d
3.一把球拍
a
a
O
x
y
v
v
P
甲
乙
t
B
-B0
B0
0
T
2T
4.一条波浪
a
a
O
x
P
v
O1
a
a
O
x
P
v
O1
O3
O2
o
A
B
v0
o1
r
r
P
Q
一颗明星
a
a
B
v0
5.一幅窗帘
v0
v0
6.一个电风扇
图15
7.一枚铜钱
如图所示为圆形区域的匀强磁场,磁感应强度为B、方向垂直纸面向里,边界跟y轴相切于坐标原点O。O点处有一放射源,沿纸面向各个方向射出速率均为v的某种带电
粒子,带电粒子在磁场中做圆周运动的半经是圆
形磁场区域半径的两倍。已知该带电粒子的质量为
m、电荷量为q,不考虑带电粒子的重力。
1、推导带电粒子在磁场空间作圆周运动的轨道半径;
2、求带电粒子通过磁场空间的最大偏角;
3、沿磁场边界放置绝缘弹性挡板,使粒子与
挡板碰撞后以原速率弹回,且其电荷量保持
不变。若从O点沿x轴正方向射入磁场的粒子
速度的已减小为v/2,求该粒子第一次回到O点
经历的时间。
X
Y
O
y
x
o
8、一沿抛物线(或直线)上升的气泡
如图所示,在xoy的平面内加有空间分布均匀、大小随时间周期性变化的电场和磁场,变化规律如乙图所示(规定竖直向上为电场强度的正方向,垂直纸面向里为磁感应强度的正方向)。在t=0时刻,质量为m、电荷量为q的带正电粒子自坐标原点O处以 0=2m/s的速度沿x轴正方向水平射出。已知电场强度, 磁感应度 ,不计粒子重力。求:
(1)1s末粒子速度的大小和方向;
(2)1s~2s内,粒子在磁场中做
圆周运动的半径和周期;
(3)画出0~4s内粒子的运动轨迹
示意图(要求:体现粒子运动特点);
(4)(2n-1)s~2ns(n=1,2,3,…)
n内粒子运动至最高点的位置坐标。
8。一沿抛物线(或直线)上升的气泡
o
y
x
1
2
3
o
y
x
1
2
3
(3)粒子在板间运动的轨迹如图2所示。
19.一串“葡萄”
如图(甲)所示,两块水平放置的平行金属板,板长L=1.4m,板距d=30cm。两板间有B=1.25T,垂直于纸面向里的匀强磁场。在两板上加如图(乙)所示的脉冲电压。在t=0时,质量m=2×10-15kg,电量为q=1×10-10C的正离子,以速度为4×103m/s从两板中间水平射入。试求:粒子在板间做什么运动?画出其轨迹。
解析 粒子重新回到O点时其运动轨道如图所示,形成一”心脏”图形.由图可知,粒子在B1中运动时间 粒子在B1中的运动时间为
10.一颗“心脏”
例2如图所示,以ab为分界面的两个匀强磁场,方向均垂直于纸面向里,其磁感应强度B1=2B2,现有一质量为m,带电量为+q的粒子,从O点沿图示方向以速度v进入B1中,经过时间t=____粒子重新回到O点(重力不计)
所以粒子运动的总时间
+
如图,在xoy平面上-H[解析]
第Ⅰ象限:
根据题意,电子在O点先会聚再发散
沿y轴正向射入的电子运动轨迹1为磁场上边界
磁场方向:
x2+(y-R)2=R2
磁场下边界2应满足:
实线1、2的交集为第1象限内的磁场区域:
由B1qv=mv2/2H得磁场大小:
磁场大小:
可以看成是第1象限的逆过程
第Ⅲ象限:
磁场方向:
由对称得:
第Ⅱ象限
第Ⅴ象限
磁场大小:
磁场方向:
垂直纸面向外
B1=mv/2eH
B4=mv/2eH
垂直纸面向里
垂直纸面向外
B3=mv/eH
垂直纸面向里
B2=mv/eH
[欣赏]磁场区域像一只漂亮蝴蝶,赏心悦目!
11.一只漂亮的蝴蝶
12.一个古朴的窗口
如图所示,与纸面垂直的竖直面MN的左侧空间中存在竖直向上场强大小为E=2.5×102N/C的匀强电场(上、下及左侧无界)。一个质量为m=0.5kg、电量为q=2.0×10—2C的可视为质点的带正电小球,在t=0时刻以大小为v0的水平初速度向右通过电场中的一点P,当t=t1时刻在电场所在空间中加上一如图所示随时间周期性变化的磁场,使得小球能竖直向下通过D点,D为电场中小球初速度方向上的一点,PD间距为L,D到竖直面MN的距离DQ为L/π。设磁感应强度垂直纸面向里为正。(g=10m/s2)
(1)如果磁感应强度B0为已知量,试推出满足条件时t1的表达式(用题中所给物理量的符号表示)
(2)若小球能始终在电场所在空间做周期性运动。则当小球运动的周期最大时,求出磁感应强度B0及运动的最大周期T的大小
v0
E
B0
P
D
M
N
Q
0
B
B0
t1+3t0
t1
t1+t0
t1+2t0
t
M
N
1.3带电粒子在磁场中运动
1.带电粒子在匀强磁场中
运动( ),只受洛伦兹
力作用,做 .
简单回顾
2.洛伦兹力提供向心力:
半径:
带电粒子在匀强磁场中的运动规律
周期:
匀速圆周运动
o
v
F
-
一.两个公式:
V
V
V
V
带电粒子做圆周运动的分析方法
V
V
一、带电粒子做圆周运动的分析方法
二、几个重要的几何关系:四点三角两三角(形)一根线(半径):
A
v
v
O’
α
B
θ
θ
θ‘
Φ(偏向角)
粒子速度的偏向角φ等与圆心角α,并等于AB弦与切线的夹角θ(弦切角)的2倍.即φ=α=2θ
(四点三角两形一线)
带电粒子做圆周运动的分析方法
三、解题步骤:画轨、定心、求半径
1.定心方法:
(1)两v(径)定心:已知入射方向和出射方向, 与速度垂直的半径交点就是圆弧轨道的圆心。
(2)一径一弦定心:已知入射方向和出射点的位置时,半径与弦中垂线的交点就是圆弧轨道的圆心。
V
P
M
O
V0
P
M
O
V
(3)若仅知道粒子进入磁场前与离开磁场后的速度方向,
可找两速度方向延长线夹角的平分线以确定圆心的位置范围,
再结合其他条件确定圆心的准确位置。
带电粒子做圆周运动的分析方法
2、求半径: 一般利用几何知识,常用解三角形的方法。
运动时间:
四、运动时间的求解:
A
v
v
O’
α
B
θ
θ
θ‘
Φ(偏向角)
粒子速度的偏向角φ
等于圆心角α
五、关注三类典型问题
1.带电粒子在有界磁场中做圆弧运动;
2.带电粒子在磁场中运动时的一些临界问题的讨论
3.多解问题
带电粒子在磁场中运动
v
v
v
v
v
v
v
v
v
v
v
v
v
(一).带电粒子在单边界磁场中的运动
①粒子的出射角和入射角相等
②如果与磁场边界成夹角θ进入,则运动轨迹所对的弦长L=2Rsinθ
O
B
A
.
r
r
P
θ
M
N
B
O
2θ
θ
二.平行直线边界
①速度较小时,作半圆运动后从原边界飞出;②速度增加为某临界值时,粒子作部分圆周运动其轨迹与另一边界相切;③速度较大时粒子作部分圆周运动后从另一边界飞出
S
B
P
S
S
Q
P
Q
Q
①速度较小时,作圆周运动通过射入点;②速度增加为某临界值时,粒子作圆周运动其轨迹与另一边界相切;③速度较大时粒子作部分圆周运动后从另一边界飞出
圆心在过入射点跟跟速度方向垂直的直线上
圆心在过入射点跟边界垂直的直线上(沿边界线入场)
圆心在磁场原边界上(垂直入场)
量变积累到一定程度发生质变,出现临界状态
P
①速度较小时,作圆弧运动后从原边界飞出;②速度增加为某临界值时,粒子作部分圆周运动其轨迹与另一边界相切;③速度较大时粒子作部分圆周运动后从另一边界飞出
三、垂直边界
例. 一个质量为m电荷量为q的带电粒子从x轴上的P(a,0)点以速度v,沿与x正方向成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴射出第一象限。求:
(1)匀强磁场的磁感应强度B和射出点的坐标。
(2)带电粒子在磁场中的运动时间是多少?
y
x
o
B
v
v
a
O/
解:(1)
四、矩形边界磁场
o
B
d
a
b
c
θ
B
圆心在磁场原边界上
圆心在过入射点跟速度方向垂直的直线上
①速度较小时粒子作半圆运动后从原边界飞出;②速度在某一范围内时从侧面边界飞出;③速度较大时粒子作部分圆周运动从对面边界飞出。
①速度较小时粒子做部分圆周运动后从原边界飞出;②速度在某一范围内从上侧面边界飞;③速度较大时粒子做部分圆周运动从右侧面边界飞出;④速度更大时粒子做部分圆周运动从下侧面边界飞出。
量变积累到一定程度发生质变,出现临界状态(轨迹与边界相切)
究竟从哪个边先出还要看边界的长宽
V0
O
a
b
c
d
θ
300
600
●
●
五.圆形边界
B
θ
θ
O’
O
入射速度方向指向匀强磁场区域圆的圆心,刚出射时速度方向的反向延长线必过该区域圆的圆心.
径向入、径向出
O1
O2
O3
O4
r v
R
v
O/
O
五.圆形边界
B
θ
O’
O
θ
B
θ
θ
O’
O
径向入、径向出
偏心入、偏心出
例.如图14所示,边长为L的等边三角形ABC为两个有界匀强磁场的理想边界,三角形内的磁场方向垂直纸面向外,磁感应强度大小为B,三角形外的磁场(足够大)方向垂直纸面向里,磁感应强度大小也为B.把粒子源放在顶点A处,它将沿∠A的角平分线发射质量为m、电荷量为q、初速度为v= 的负电粒子(粒子重力不计).求:
图14
(1)从A射出的粒子第一次到达C点所用时间为多少
(2)带电粒子在题设的两个有界磁场中运动的周期.
六、三角形磁场
解析 (1)带电粒子垂直进入磁场,做匀速圆周运动
qvB=
T=
将已知条件代入有r =L
从A点到达C点的运动轨
迹如图所示,可得
tAC= T
tAC=
(2)带电粒子在一个运动的周期运动轨迹如第(1)问图所示.
粒子通过圆弧从C点运动至B点的时间为
tCB=
带电粒子运动的周期为TABC=3(tAC+tCB)
解得TABC=
答案 (1) (2)
七.环形边界
r1
O
O2
例1、如图直线MN上方有磁感应强度为B的匀强磁场。正、负电子同时从同一点O以与MN成30 角的同样速度v射入磁场(电子质量为m,电荷为e),它们从磁场中射出时相距多远?射出的时间差是多少?
M
N
B
O
v
例2、一带电质点,质量为m,电量为q,以平行于x轴的速度v从y轴上的a点射入图中第一象限所示的区域,为了使该质点能从x轴上的b点以垂直于x轴的速度v射出,可在适当的地方加一个垂直于xy平面、磁感强度为B的匀强磁场。若此磁场仅分布在一个圆形区域内,试求这圆形磁场区域的最小半径。重力忽略不计
例3、如图,在一水平放置的平板MN上方有匀强磁场,磁感应强度的大小为B,磁场方向垂直于纸面向里,许多质量为m,带电量为+q的粒子,以相同的速率v沿位于纸面内的各个方向,由小孔O射入磁场区域,不计重力,不计粒子间的相互影响。下列图中阴影部分表示带电粒子可能经过的区域,其中R=mv/qB。哪个图是正确的 ( )
2R
R
2R
M
N
O
2R
R
2R
M
N
O
2R
2R
2R
M
N
O
R
2R
2R
M
N
O
D.
A.
B.
C.
A
M
N
B
O
B
M
B
O
v
……以速率 v 沿纸面各个方向由小孔O射入磁场
B
v
F
B
v
F
B
v
2R
R
2R
M
N
O
解:带电量为+q的粒子,以相同的速率v沿位于纸面内的各个方向,由小孔 O 射入磁场区域,由R=mv/qB,各个粒子在磁场中运动的半径均相同,
在磁场中运动的轨迹圆圆心是在以O为圆心、以R=mv/qB为半径的1/2圆弧上,如图虚线示:
各粒子的运动轨迹如图实线示:
带电粒子可能经过的区域阴影部分如图斜线示
例4、核聚变反应需要几百万度以上的高温,为把高温条件下高速运动的离子约束在小范围内(否则不可能发生核反应),通常采用磁约束的方法(托卡马克装置)。如图所示,环状匀强磁场围成中空区域,中空区域中的带电粒子只要速度不是很大,都不会穿出磁场的外边缘而被约束在该区域内。设环状磁场的内半径为R1=0.5m,外半径R2=1.0m,磁场的磁感强度B=1.0T,若被束缚带电粒子的荷质比为q/m=4×107C/㎏,中空区域内带电粒子具有各个方向的速度。试计算
(1)粒子沿环状的半径方向射入磁场,不能穿越磁场的最大速度。
(2)所有粒子不能穿越磁场的最大速度。
解析:(1)要粒子沿环状的半径方向射入磁场,不能穿越磁场,则粒子的临界轨迹必须要与外圆相切,轨迹如图所示。
由图中知,
解得
由
得
r1
所以粒子沿环状的半径方向射入磁场,不能穿越磁场的最
大速度为
O
O2
(2)当粒子以V2的速度沿与内圆相切方向射入磁场且轨道与外圆相切时,则以V2速度沿各方向射入磁场区的粒子都不能穿出磁场边界,如图所示。
由图中知
由 得
所以所有粒子不能穿越磁场的最大速度
带电粒子在有“圆孔”的磁场中运动
例5、在如图所示的平面直角坐标系xoy中,有一个圆形区域的匀强磁场(图中未画出),磁场方向垂直于xoy平面,O点为该圆形区域边界上的一点。现有一质量为m,带电量为+q的带电粒子(重力不计)从O点以初速度vo沿+x方向进入磁场,已知粒子经过y轴上P点时速度方向与+y方向夹角为θ=30 ,OP=L 求:⑴磁感应强度的大小和方向 ⑵该圆形磁场区域的最小面积。
O
y
x
P
v0
v0
θ
L
分析: OP的垂直平分线与v0的反向延长线交于Q, 作OQ的垂直平分线与OP相交于O′, O′即带电粒子运动轨迹圆的圆心。带电粒子在磁场中所做的是1/3圆周的匀速圆周运动。
O
y
x
P
v0
v0
θ
O′
Q
不确定边界问题
O
y
x
P
v0
v0
θ
解:(1)由左手定则得磁场方向垂直xoy平面向里,粒子在磁场中所做的是1/3圆周的匀速圆周运动,如图所示,粒子在Q点飞出磁场,设其圆心为O′,半径为R,
Q
O′
L
120°
θ
(L-R)sin30°=R……… ① ∴ R=L/3
…… ②
① ②得
(2)由图得
例6 、如图所示,现有一质量为m、电量为e的电子从y轴上的P(0,a)点以初速度v0平行于x轴射出,为了使电子能够经过x轴上的Q(b,0)点,可在y轴右侧加一垂直于xOy平面向里、宽度为L的匀强磁场,磁感应强度大小为B,该磁场左、右边界与y轴平行,上、下足够宽(图中未画出)。已知,
L<b。试求磁场的左边界距坐标原点的可能距离。
(结果可用反三角函数表示)
x
y
0
Q
v0
P
解:
x
y
0
Q
v0
P
图1
设电子在磁场中作圆周运动的轨道半径为r, 则
①
解得 ②
⑴当r>L时,磁场区域及电子运动轨迹如图1所示,
θ
θ
由几何关系有 ③
则磁场左边界距坐标原点的距离为
④
(其中 ) ⑤
②当r
y
0
Q
v0
P
图2
由几何关系得磁场左边界距坐标原点的距离为
解得 ⑦
反思总结
返回
小结
1.带电粒子进入有界磁场,运动轨迹为一段弧线.
2.当同源粒子垂直进入磁场的运动轨迹
3.注意圆周运动中的有关对称规律:
(2) 粒子进入单边磁场时,入射速度与边界夹角等于出射速度与边界的夹角;
(1) 在圆形磁场区域内,沿径向射入的粒子,必沿径向射出.
4、带电粒子在磁场中运动问题的解题思路
找圆心
画轨迹
已知两点速度方向(两径找心)
已知一点速度方向和另一点位置
(一径一弦找心)
两洛伦兹力方向的延长线交点为圆心
弦的垂直平分线与一直径的交点为圆心
v1
O
v2
A
B
v1
A
B
O
求半径
O3
r
r
O4
r
r
O2
r
r
O1
r
r
O
S
1.一朵梅花
带电粒子在磁场中运动轨迹赏析
带电粒子在复合场中运动的轨迹欣赏
r
x
y
y
2.一座“拱桥”
(重力不计)
O1
O2
O3
L
d
3.一把球拍
a
a
O
x
y
v
v
P
甲
乙
t
B
-B0
B0
0
T
2T
4.一条波浪
a
a
O
x
P
v
O1
a
a
O
x
P
v
O1
O3
O2
o
A
B
v0
o1
r
r
P
Q
一颗明星
a
a
B
v0
5.一幅窗帘
v0
v0
6.一个电风扇
图15
7.一枚铜钱
如图所示为圆形区域的匀强磁场,磁感应强度为B、方向垂直纸面向里,边界跟y轴相切于坐标原点O。O点处有一放射源,沿纸面向各个方向射出速率均为v的某种带电
粒子,带电粒子在磁场中做圆周运动的半经是圆
形磁场区域半径的两倍。已知该带电粒子的质量为
m、电荷量为q,不考虑带电粒子的重力。
1、推导带电粒子在磁场空间作圆周运动的轨道半径;
2、求带电粒子通过磁场空间的最大偏角;
3、沿磁场边界放置绝缘弹性挡板,使粒子与
挡板碰撞后以原速率弹回,且其电荷量保持
不变。若从O点沿x轴正方向射入磁场的粒子
速度的已减小为v/2,求该粒子第一次回到O点
经历的时间。
X
Y
O
y
x
o
8、一沿抛物线(或直线)上升的气泡
如图所示,在xoy的平面内加有空间分布均匀、大小随时间周期性变化的电场和磁场,变化规律如乙图所示(规定竖直向上为电场强度的正方向,垂直纸面向里为磁感应强度的正方向)。在t=0时刻,质量为m、电荷量为q的带正电粒子自坐标原点O处以 0=2m/s的速度沿x轴正方向水平射出。已知电场强度, 磁感应度 ,不计粒子重力。求:
(1)1s末粒子速度的大小和方向;
(2)1s~2s内,粒子在磁场中做
圆周运动的半径和周期;
(3)画出0~4s内粒子的运动轨迹
示意图(要求:体现粒子运动特点);
(4)(2n-1)s~2ns(n=1,2,3,…)
n内粒子运动至最高点的位置坐标。
8。一沿抛物线(或直线)上升的气泡
o
y
x
1
2
3
o
y
x
1
2
3
(3)粒子在板间运动的轨迹如图2所示。
19.一串“葡萄”
如图(甲)所示,两块水平放置的平行金属板,板长L=1.4m,板距d=30cm。两板间有B=1.25T,垂直于纸面向里的匀强磁场。在两板上加如图(乙)所示的脉冲电压。在t=0时,质量m=2×10-15kg,电量为q=1×10-10C的正离子,以速度为4×103m/s从两板中间水平射入。试求:粒子在板间做什么运动?画出其轨迹。
解析 粒子重新回到O点时其运动轨道如图所示,形成一”心脏”图形.由图可知,粒子在B1中运动时间 粒子在B1中的运动时间为
10.一颗“心脏”
例2如图所示,以ab为分界面的两个匀强磁场,方向均垂直于纸面向里,其磁感应强度B1=2B2,现有一质量为m,带电量为+q的粒子,从O点沿图示方向以速度v进入B1中,经过时间t=____粒子重新回到O点(重力不计)
所以粒子运动的总时间
+
如图,在xoy平面上-H
第Ⅰ象限:
根据题意,电子在O点先会聚再发散
沿y轴正向射入的电子运动轨迹1为磁场上边界
磁场方向:
x2+(y-R)2=R2
磁场下边界2应满足:
实线1、2的交集为第1象限内的磁场区域:
由B1qv=mv2/2H得磁场大小:
磁场大小:
可以看成是第1象限的逆过程
第Ⅲ象限:
磁场方向:
由对称得:
第Ⅱ象限
第Ⅴ象限
磁场大小:
磁场方向:
垂直纸面向外
B1=mv/2eH
B4=mv/2eH
垂直纸面向里
垂直纸面向外
B3=mv/eH
垂直纸面向里
B2=mv/eH
[欣赏]磁场区域像一只漂亮蝴蝶,赏心悦目!
11.一只漂亮的蝴蝶
12.一个古朴的窗口
如图所示,与纸面垂直的竖直面MN的左侧空间中存在竖直向上场强大小为E=2.5×102N/C的匀强电场(上、下及左侧无界)。一个质量为m=0.5kg、电量为q=2.0×10—2C的可视为质点的带正电小球,在t=0时刻以大小为v0的水平初速度向右通过电场中的一点P,当t=t1时刻在电场所在空间中加上一如图所示随时间周期性变化的磁场,使得小球能竖直向下通过D点,D为电场中小球初速度方向上的一点,PD间距为L,D到竖直面MN的距离DQ为L/π。设磁感应强度垂直纸面向里为正。(g=10m/s2)
(1)如果磁感应强度B0为已知量,试推出满足条件时t1的表达式(用题中所给物理量的符号表示)
(2)若小球能始终在电场所在空间做周期性运动。则当小球运动的周期最大时,求出磁感应强度B0及运动的最大周期T的大小
v0
E
B0
P
D
M
N
Q
0
B
B0
t1+3t0
t1
t1+t0
t1+2t0
t
M
N
