2021-2022学年人教版八年级数学下册17.2勾股定理的逆定理练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.2勾股定理的逆定理练习题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 161.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-26 21:52:33 | ||
图片预览

文档简介
17.2 勾股定理的逆定理 练习题
一、选择题
1.满足下列条件的△ABC,不是直角三角形的是( )
A.b2﹣c2=a2 B.a:b:c=3:4:5
C.∠C=∠A﹣∠B D.∠A:∠B:∠C=9:12:15
2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,, B.1,, C.6,7,8 D.2,3,4
3.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三条边的比是1∶2∶3 B.三条边满足关系a2=c2-b2
C.三个角的比是1∶2∶3 D.三个角满足关系∠B+∠C=∠A
4.如图,正方形ABCD的面积是( )
A.5 B.25 C.7 D.1
5.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三条边的比为2∶3∶4 B.三条边满足关系a2=b2﹣c2
C.三条边的比为1∶1∶ D.三个角满足关系∠B+∠C=∠A
6.若一个三角形的三边长分别是15,20,25,则这个三角形最长的边上的高等于( )
A.10 B.11 C.12 D.13
7.如图,在4×4的正方形网格中有两个格点A,B,连接AB,在网格中再找一个格点C,使得△ABC是等腰直角三角形,则满足条件的格点C的个数是( )
A.1个 B.2个 C.3个 D.4个
8.若△ABC的三边a、b、c满足条件(a﹣b)(a2+b2﹣c2)=0,则△ABC为( )
A.等腰三角形 B.直角三角形
C.等腰三角形或直角三角形 D.等腰直角三角形
9.下列几组数能作为直角三角形的三边长的是( )
A.5,12,13 B.7,12,15 C.12,15,20 D.12,18,22
10.下列各组数中,不能作为直角三角形的三边长的是( )
A.3,4,5 B.4,5,6 C.5,12,13 D.6,8,10
二、填空题
11.“直角三角形的两个锐角互余”的逆命题是 。
12.根据下列已知条件,能确定△ABC的大小和形状的是
①AB=3,BC=4,AC=5 ②AB=4,BC=3,∠A=30
③∠A=60 ,∠B=45 ,AB=4 ④∠C=90 ,AB=6,AC=5
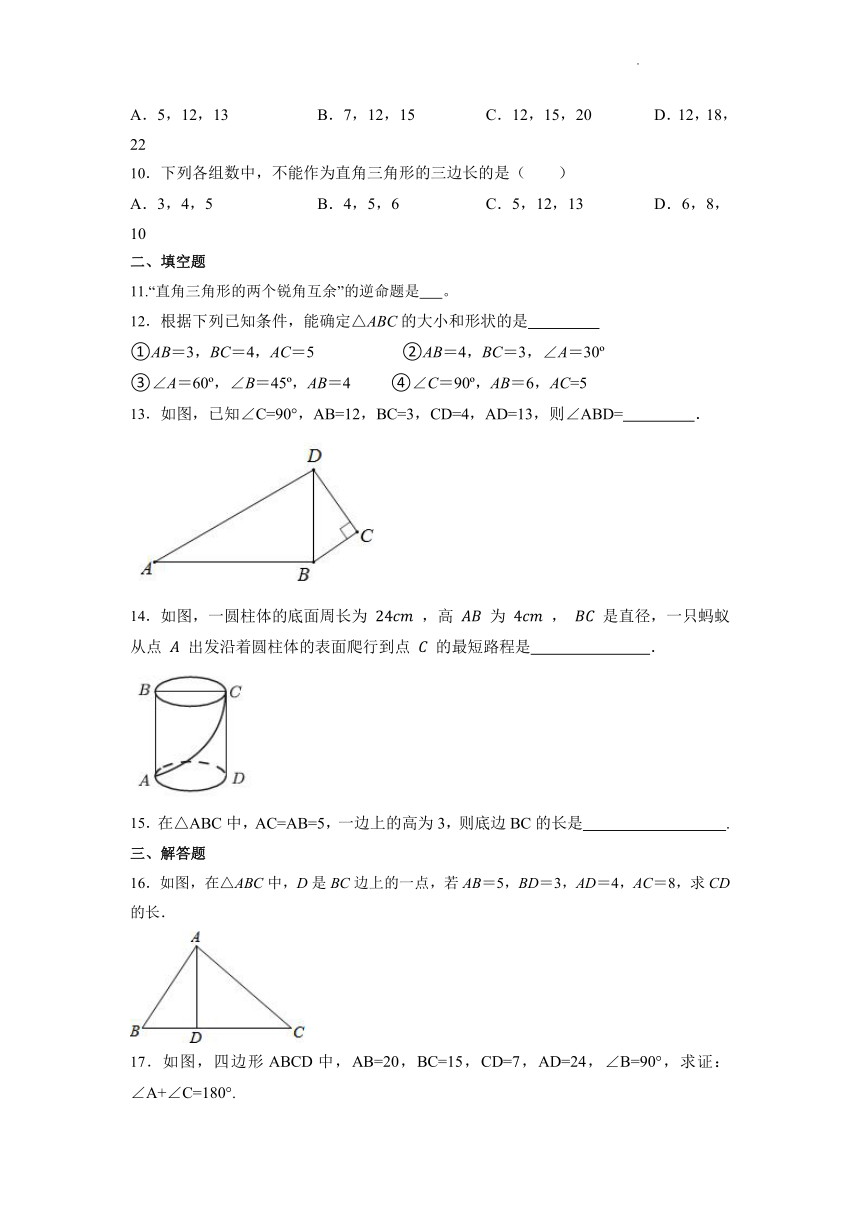
13.如图,已知∠C=90°,AB=12,BC=3,CD=4,AD=13,则∠ABD= .
14.如图,一圆柱体的底面周长为 ,高 为 , 是直径,一只蚂蚁从点 出发沿着圆柱体的表面爬行到点 的最短路程是 .
15.在△ABC中,AC=AB=5,一边上的高为3,则底边BC的长是 .
三、解答题
16.如图,在△ABC中,D是BC边上的一点,若AB=5,BD=3,AD=4,AC=8,求CD的长.
17.如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求证:∠A+∠C=180°.
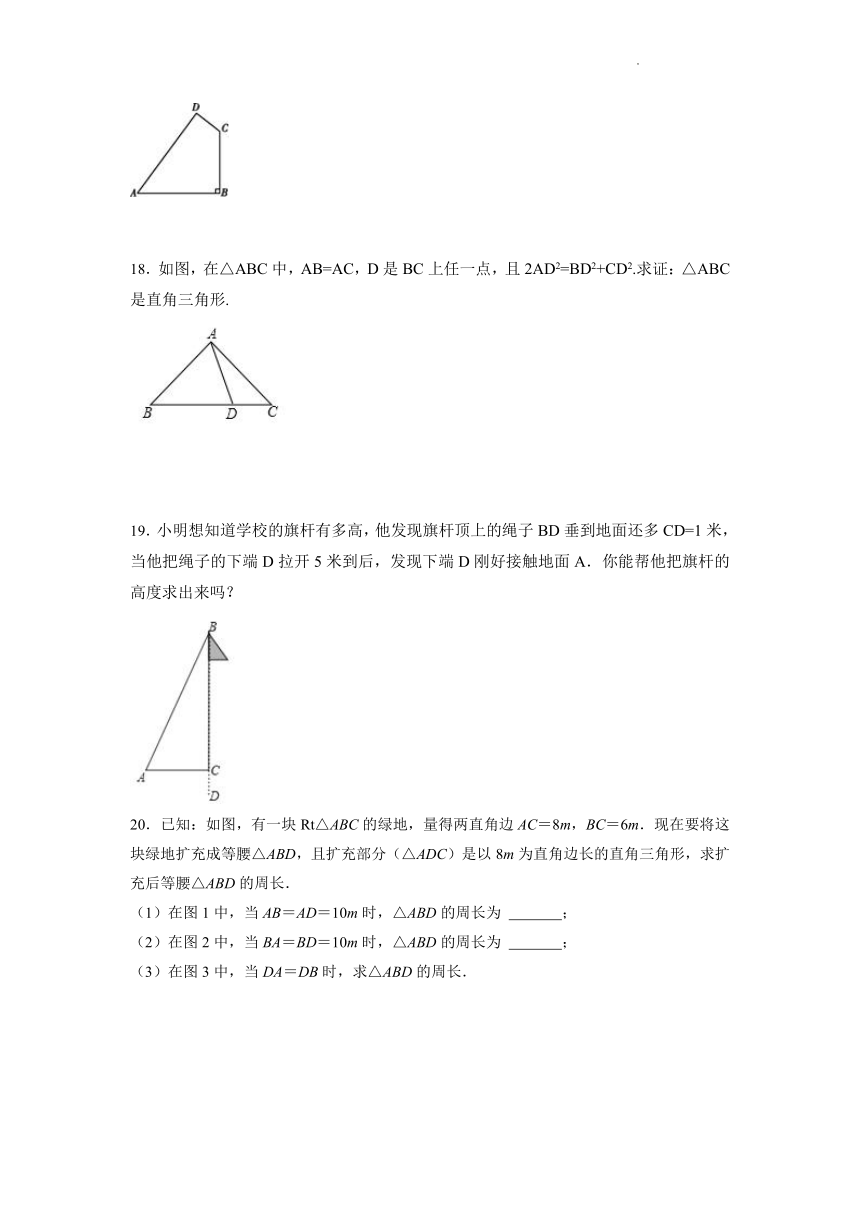
18.如图,在△ABC中,AB=AC,D是BC上任一点,且2AD2=BD2+CD2.求证:△ABC是直角三角形.
19.小明想知道学校的旗杆有多高,他发现旗杆顶上的绳子BD垂到地面还多CD=1米,当他把绳子的下端D拉开5米到后,发现下端D刚好接触地面A.你能帮他把旗杆的高度求出来吗?
20.已知:如图,有一块Rt△ABC的绿地,量得两直角边AC=8m,BC=6m.现在要将这块绿地扩充成等腰△ABD,且扩充部分(△ADC)是以8m为直角边长的直角三角形,求扩充后等腰△ABD的周长.
(1)在图1中,当AB=AD=10m时,△ABD的周长为 ;
(2)在图2中,当BA=BD=10m时,△ABD的周长为 ;
(3)在图3中,当DA=DB时,求△ABD的周长.
21.已知△ABC中,∠C=90°,BC=3cm,BD=12cm,AD=13cm,△ABC的面积是6cm2.
(1)求AB的长度;
(2)求△ABD的面积.
22.如图,点A是网红打卡地诗博园,市民可在云龙湖边的游客观光车站B或C处乘车前往,且AB=BC,因市政建设,点C到点A段现暂时封闭施工,为方便出行,在湖边的H处修建了一临时车站(点H在线段BC上),由H处亦可直达A处,若AC=1km,AH=0.8km,CH=0.6km.
(1)判断△ACH的形状,并说明理由;
(2)求路线AB的长.
23.笔直的河流一侧有一营地C,河边有两个漂流点A,B、其中AB=AC,由于周边施工,由C到A的路现在已经不通,为方便游客,在河边新建一个漂流点H(A,H,B在同一直线上),并新修一条路CH,测得BC=10千米,CH=8千米,BH=6千米.
(1)判断△BCH的形状,并说明理由;
(2)求原路线AC的长.
【参考答案】
1.D
2.B
3.A
4.B
5.A
6.C
7.C
8.C
9.A
10.B
11. 有两个(锐)角互余的三角形是直角三角形
12.①③④
13.90°
14.
15.8或 或
16.
17.解:(1)∵CD是AB边上高,∴∠CDA=∠CDB=90°,
∴AC===20,BC===15,
∵AB=AD+BD=25,∴△ABC的周长=AB+BC+AC=25+20+15=60;
(2)△ABC是直角三角形,理由如下:202+152=252,
即AC2+BC2=AB2,∴△ABC是直角三角形.
18.解:连接AC,过点C作CE⊥AB于点E.∵AD⊥CD,∴∠D=90°.
在Rt△ACD中,AD=5,CD=12,AC=.
∵BC=13,∴AC=BC.∵CE⊥AB,AB=10,∴AE=BE=AB=.
在Rt△CAE中,CE=.
∴S四边形ABCD=S△DAC+S△ABC=.
19.
20.解:(1)如图1,∵AB=AD=10m,AC⊥BD,AC=8m,
∴DC==6(m),
则△ABD的周长为:10+10+6+6=32(m).
故答案为:32m;
(2)如图2,当BA=BD=10m时,
则DC=BD﹣BC=10﹣6=4(m),
故AD==4(m),
则△ABD的周长为:AD+AB+BD=10+4+10=(20+4)m;
故答案为:(20+4)m;
(3)如图3,∵DA=DB,
∴设DC=xm,则AD=(6+x)m,
∴DC2+AC2=AD2,
即x2+82=(6+x)2,
解得;x=,
∵AC=8m,BC=6m,
∴AB=10m,
故△ABD的周长为:AD+BD+AB=2×(+6)+10=(m).
21.解:(1)过点C作CE⊥AB于点E,
∴∠CEB=90°,
∵∠B=30°,BC=30米,
∴CE=BC=15(米)
∴点C到AB的距离是15米;
(2)∵AD⊥CD,
∴∠ADC=90°,
∵∠ACD=60°,∠B=30°,
∴∠CAD=90°﹣∠ACD=30°,∠BAC=∠ACD﹣∠B=30°,
∴∠CAD=∠BAC,
∵CE⊥AB,
∴CD=CE=15米,
在Rt△ACD中,∠CAD=30°,CD=15米,
∴CD=AC,
∴AC=CD=2×15=30(米),
由勾股定理得:AD===15(米),
答:线段AD的长度是15米.
22.(1)△ACH是直角三角形;(2)路线AB的长为km.
23.(1)△HBC是直角三角形;(2)原来的路线AC的长为千米
一、选择题
1.满足下列条件的△ABC,不是直角三角形的是( )
A.b2﹣c2=a2 B.a:b:c=3:4:5
C.∠C=∠A﹣∠B D.∠A:∠B:∠C=9:12:15
2.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
A.,, B.1,, C.6,7,8 D.2,3,4
3.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三条边的比是1∶2∶3 B.三条边满足关系a2=c2-b2
C.三个角的比是1∶2∶3 D.三个角满足关系∠B+∠C=∠A
4.如图,正方形ABCD的面积是( )
A.5 B.25 C.7 D.1
5.下列条件中,不能判断一个三角形是直角三角形的是( )
A.三条边的比为2∶3∶4 B.三条边满足关系a2=b2﹣c2
C.三条边的比为1∶1∶ D.三个角满足关系∠B+∠C=∠A
6.若一个三角形的三边长分别是15,20,25,则这个三角形最长的边上的高等于( )
A.10 B.11 C.12 D.13
7.如图,在4×4的正方形网格中有两个格点A,B,连接AB,在网格中再找一个格点C,使得△ABC是等腰直角三角形,则满足条件的格点C的个数是( )
A.1个 B.2个 C.3个 D.4个
8.若△ABC的三边a、b、c满足条件(a﹣b)(a2+b2﹣c2)=0,则△ABC为( )
A.等腰三角形 B.直角三角形
C.等腰三角形或直角三角形 D.等腰直角三角形
9.下列几组数能作为直角三角形的三边长的是( )
A.5,12,13 B.7,12,15 C.12,15,20 D.12,18,22
10.下列各组数中,不能作为直角三角形的三边长的是( )
A.3,4,5 B.4,5,6 C.5,12,13 D.6,8,10
二、填空题
11.“直角三角形的两个锐角互余”的逆命题是 。
12.根据下列已知条件,能确定△ABC的大小和形状的是
①AB=3,BC=4,AC=5 ②AB=4,BC=3,∠A=30
③∠A=60 ,∠B=45 ,AB=4 ④∠C=90 ,AB=6,AC=5
13.如图,已知∠C=90°,AB=12,BC=3,CD=4,AD=13,则∠ABD= .
14.如图,一圆柱体的底面周长为 ,高 为 , 是直径,一只蚂蚁从点 出发沿着圆柱体的表面爬行到点 的最短路程是 .
15.在△ABC中,AC=AB=5,一边上的高为3,则底边BC的长是 .
三、解答题
16.如图,在△ABC中,D是BC边上的一点,若AB=5,BD=3,AD=4,AC=8,求CD的长.
17.如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,求证:∠A+∠C=180°.
18.如图,在△ABC中,AB=AC,D是BC上任一点,且2AD2=BD2+CD2.求证:△ABC是直角三角形.
19.小明想知道学校的旗杆有多高,他发现旗杆顶上的绳子BD垂到地面还多CD=1米,当他把绳子的下端D拉开5米到后,发现下端D刚好接触地面A.你能帮他把旗杆的高度求出来吗?
20.已知:如图,有一块Rt△ABC的绿地,量得两直角边AC=8m,BC=6m.现在要将这块绿地扩充成等腰△ABD,且扩充部分(△ADC)是以8m为直角边长的直角三角形,求扩充后等腰△ABD的周长.
(1)在图1中,当AB=AD=10m时,△ABD的周长为 ;
(2)在图2中,当BA=BD=10m时,△ABD的周长为 ;
(3)在图3中,当DA=DB时,求△ABD的周长.
21.已知△ABC中,∠C=90°,BC=3cm,BD=12cm,AD=13cm,△ABC的面积是6cm2.
(1)求AB的长度;
(2)求△ABD的面积.
22.如图,点A是网红打卡地诗博园,市民可在云龙湖边的游客观光车站B或C处乘车前往,且AB=BC,因市政建设,点C到点A段现暂时封闭施工,为方便出行,在湖边的H处修建了一临时车站(点H在线段BC上),由H处亦可直达A处,若AC=1km,AH=0.8km,CH=0.6km.
(1)判断△ACH的形状,并说明理由;
(2)求路线AB的长.
23.笔直的河流一侧有一营地C,河边有两个漂流点A,B、其中AB=AC,由于周边施工,由C到A的路现在已经不通,为方便游客,在河边新建一个漂流点H(A,H,B在同一直线上),并新修一条路CH,测得BC=10千米,CH=8千米,BH=6千米.
(1)判断△BCH的形状,并说明理由;
(2)求原路线AC的长.
【参考答案】
1.D
2.B
3.A
4.B
5.A
6.C
7.C
8.C
9.A
10.B
11. 有两个(锐)角互余的三角形是直角三角形
12.①③④
13.90°
14.
15.8或 或
16.
17.解:(1)∵CD是AB边上高,∴∠CDA=∠CDB=90°,
∴AC===20,BC===15,
∵AB=AD+BD=25,∴△ABC的周长=AB+BC+AC=25+20+15=60;
(2)△ABC是直角三角形,理由如下:202+152=252,
即AC2+BC2=AB2,∴△ABC是直角三角形.
18.解:连接AC,过点C作CE⊥AB于点E.∵AD⊥CD,∴∠D=90°.
在Rt△ACD中,AD=5,CD=12,AC=.
∵BC=13,∴AC=BC.∵CE⊥AB,AB=10,∴AE=BE=AB=.
在Rt△CAE中,CE=.
∴S四边形ABCD=S△DAC+S△ABC=.
19.
20.解:(1)如图1,∵AB=AD=10m,AC⊥BD,AC=8m,
∴DC==6(m),
则△ABD的周长为:10+10+6+6=32(m).
故答案为:32m;
(2)如图2,当BA=BD=10m时,
则DC=BD﹣BC=10﹣6=4(m),
故AD==4(m),
则△ABD的周长为:AD+AB+BD=10+4+10=(20+4)m;
故答案为:(20+4)m;
(3)如图3,∵DA=DB,
∴设DC=xm,则AD=(6+x)m,
∴DC2+AC2=AD2,
即x2+82=(6+x)2,
解得;x=,
∵AC=8m,BC=6m,
∴AB=10m,
故△ABD的周长为:AD+BD+AB=2×(+6)+10=(m).
21.解:(1)过点C作CE⊥AB于点E,
∴∠CEB=90°,
∵∠B=30°,BC=30米,
∴CE=BC=15(米)
∴点C到AB的距离是15米;
(2)∵AD⊥CD,
∴∠ADC=90°,
∵∠ACD=60°,∠B=30°,
∴∠CAD=90°﹣∠ACD=30°,∠BAC=∠ACD﹣∠B=30°,
∴∠CAD=∠BAC,
∵CE⊥AB,
∴CD=CE=15米,
在Rt△ACD中,∠CAD=30°,CD=15米,
∴CD=AC,
∴AC=CD=2×15=30(米),
由勾股定理得:AD===15(米),
答:线段AD的长度是15米.
22.(1)△ACH是直角三角形;(2)路线AB的长为km.
23.(1)△HBC是直角三角形;(2)原来的路线AC的长为千米
