方程的根与函数的零点
图片预览




文档简介
课件20张PPT。 3.1.1方程的根
与
函数的零点 思考:一元二次方程
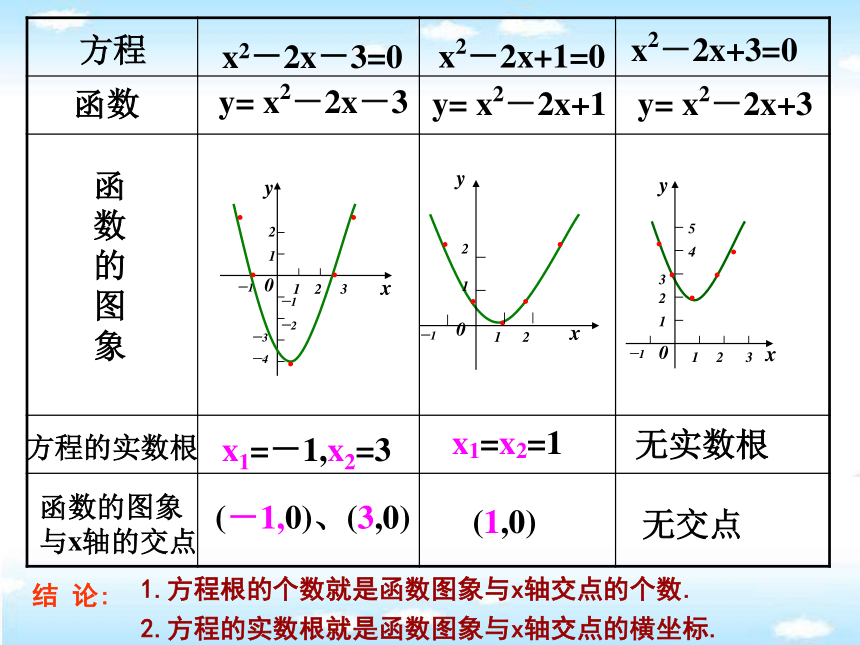
ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图象有什么关系?方程x2-2x+1=0x2-2x+3=0y= x2-2x-3y= x2-2x+1函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+31.方程根的个数就是函数图象与x轴交点的个数.结 论: 2.方程的实数根就是函数图象与x轴交点的横坐标.方程ax2 +bx+c=0
(a≠0)的根函数y= ax2 +bx
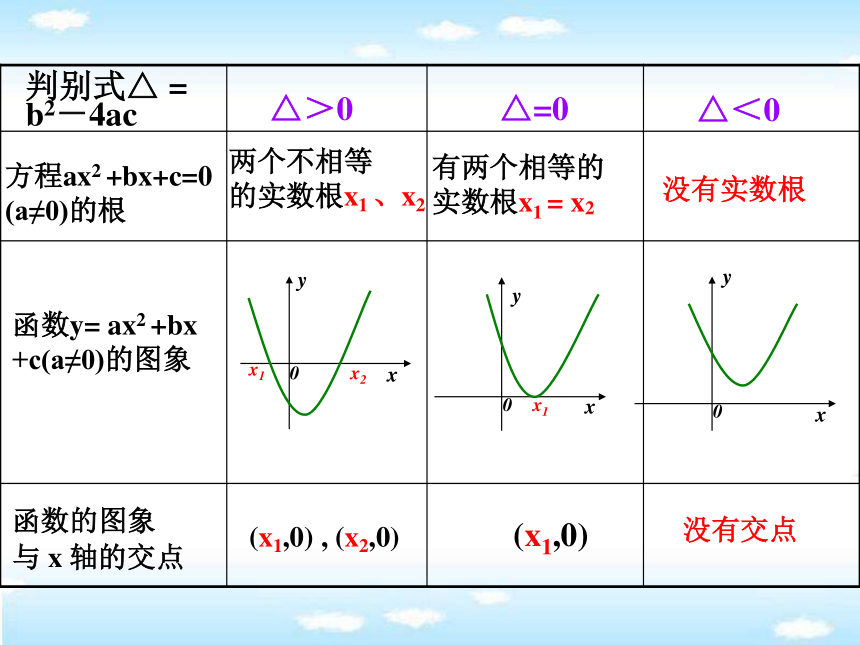
+c(a≠0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
的实数根x1 、x2 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.函数零点的定义:注意:零点指的是一个实数.方程x2-2x+1=0x2-2x+3=0y= x2-2x-3y= x2-2x+1函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+3
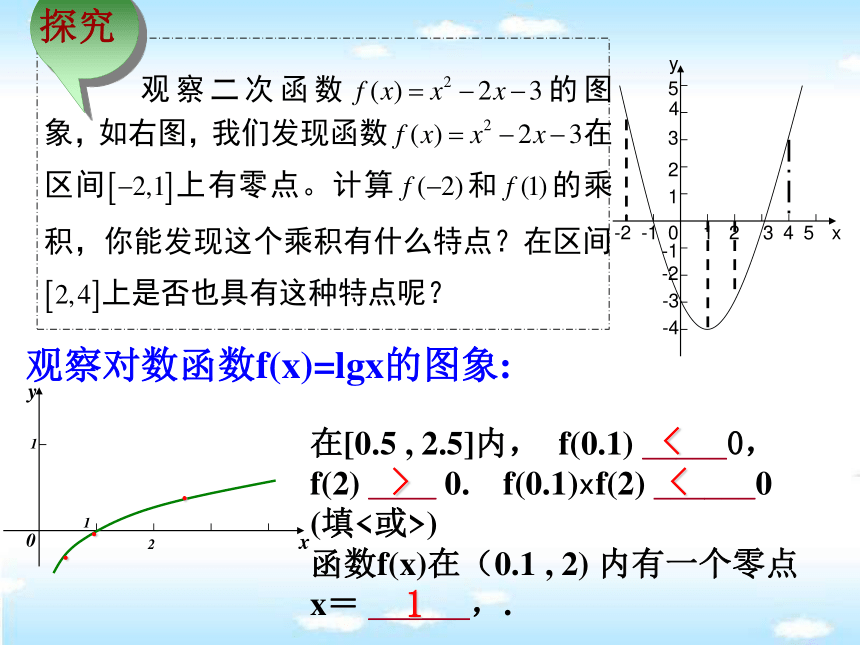
方程f(x)=0有实数根等价关系y=-x2-x+20; (2)y=2x-1; 拓展:求下列函数的零点. 评注:求函数的零点就是求相应的方程的根.012345-1-212345-1-2-3-4xy探究观察对数函数f(x)=lgx的图象:在[0.5 , 2.5]内, f(0.1) _____0, f(2) ____ 0. f(0.1)xf(2) ______0
(填<或>)
函数f(x)在(0.1 , 2) 内有一个零点 x= ______,.<><1结论例→在(a,b)内有零点注:反过来不一定成立10个1个1.若函数y=5x2-7x-1在区间[a,b]上的图象是连续不断的曲线,且函数y=5x2-7x-1在(a,b)内有零点,则f(a)·f(b)的值( )
A、大于0 B、小于0
C、无法判断 D、等于零2.函数 的零点个数是_____个由表3-1和图3.1—3可知f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内
有零点. 由于函数f(x)在定义域
(0,+∞)内是增函数,所以
它仅有一个零点.解:用计算器或计算机作出x、f(x)的对应值表(表3-1)
和图象(图3.1—3)-4 -1.30691.09863.38635.60947.79189.945912.079414.1972abx1x2x4x3cdeyx例方法二:法二由图可得两函数图象只有一个公共点,所以函数只有一个零点.求函数f(x)=lnx+2x-6的零点个数 方法三:求函数 的零点的个数小技巧:
lnx的零点所在区间常常与(2,3)有关练习:练 习:
(有,一个)课堂练习2. 函数f(x)=x3+x-1在下列哪个区间有零点( )
A.(-2,-1) B.(0,1)
C.(1,2) D.(2,3)1.函数 f(x)=x3-3x+2 的零点为( )
A.-1,1,2 B.-2,-1,1
C.-2,1 D.-1,23.已知函数f(x)=x2-ax-2
(1)证明:函数有两个零点。
(2)若函数在区间[0,2]有零点,求a的取值范围.2.试推断是否存在自然数m,使函数f(x)=3-2x在区间(m,m+1)上有零点?若存在,求m的值;若不存在,说明理由. 课堂小结: 作业:
1、求下列函数的零点:(1)y=-x2+6x+7;
(2)y=x3-4x.
2、若函数f(x)=x2-ax-b的两个零点是2和3,求 loga25 + b2。1、函数零点的定义;2、函数的零点与方程的根的关系;3、确定函数的零点的方法.
ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图象有什么关系?方程x2-2x+1=0x2-2x+3=0y= x2-2x-3y= x2-2x+1函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+31.方程根的个数就是函数图象与x轴交点的个数.结 论: 2.方程的实数根就是函数图象与x轴交点的横坐标.方程ax2 +bx+c=0
(a≠0)的根函数y= ax2 +bx
+c(a≠0)的图象判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
的实数根x1 、x2 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.函数零点的定义:注意:零点指的是一个实数.方程x2-2x+1=0x2-2x+3=0y= x2-2x-3y= x2-2x+1函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象
与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+3
方程f(x)=0有实数根等价关系y=-x2-x+20; (2)y=2x-1; 拓展:求下列函数的零点. 评注:求函数的零点就是求相应的方程的根.012345-1-212345-1-2-3-4xy探究观察对数函数f(x)=lgx的图象:在[0.5 , 2.5]内, f(0.1) _____0, f(2) ____ 0. f(0.1)xf(2) ______0
(填<或>)
函数f(x)在(0.1 , 2) 内有一个零点 x= ______,.<><1结论例→在(a,b)内有零点注:反过来不一定成立10个1个1.若函数y=5x2-7x-1在区间[a,b]上的图象是连续不断的曲线,且函数y=5x2-7x-1在(a,b)内有零点,则f(a)·f(b)的值( )
A、大于0 B、小于0
C、无法判断 D、等于零2.函数 的零点个数是_____个由表3-1和图3.1—3可知f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内
有零点. 由于函数f(x)在定义域
(0,+∞)内是增函数,所以
它仅有一个零点.解:用计算器或计算机作出x、f(x)的对应值表(表3-1)
和图象(图3.1—3)-4 -1.30691.09863.38635.60947.79189.945912.079414.1972abx1x2x4x3cdeyx例方法二:法二由图可得两函数图象只有一个公共点,所以函数只有一个零点.求函数f(x)=lnx+2x-6的零点个数 方法三:求函数 的零点的个数小技巧:
lnx的零点所在区间常常与(2,3)有关练习:练 习:
(有,一个)课堂练习2. 函数f(x)=x3+x-1在下列哪个区间有零点( )
A.(-2,-1) B.(0,1)
C.(1,2) D.(2,3)1.函数 f(x)=x3-3x+2 的零点为( )
A.-1,1,2 B.-2,-1,1
C.-2,1 D.-1,23.已知函数f(x)=x2-ax-2
(1)证明:函数有两个零点。
(2)若函数在区间[0,2]有零点,求a的取值范围.2.试推断是否存在自然数m,使函数f(x)=3-2x在区间(m,m+1)上有零点?若存在,求m的值;若不存在,说明理由. 课堂小结: 作业:
1、求下列函数的零点:(1)y=-x2+6x+7;
(2)y=x3-4x.
2、若函数f(x)=x2-ax-b的两个零点是2和3,求 loga25 + b2。1、函数零点的定义;2、函数的零点与方程的根的关系;3、确定函数的零点的方法.
