2021-2022学年度人教版数学八年级下册第十七章勾股定理的逆定理(含答案)
文档属性
| 名称 | 2021-2022学年度人教版数学八年级下册第十七章勾股定理的逆定理(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 132.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 00:00:00 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版数学八年级下册第十七章勾股定理的逆定理
一、单选题
1.下列各组数中,能构成直角三角形的是( )
A. 4,5,6 B. 1,1, C. 6,8,13 D. 5,12,15
2.△ABC的三边为a,b,c且(a+b)(a﹣b)=c2 , 则该三角形是( )
A. 锐角三角形 B. 以c为斜边的直角三角形
C. 以b为斜边的直角三角形 D. 以a为斜边的直角三角形
3.在如图所示的方格纸中,点A,B,C均为格点,则的度数是( )
A. B. C. D.
4.如图有一个水池,水面BE的宽为16尺,在水池的中央有一根芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个芦苇的高度是( )
A. 26尺 B. 24尺 C. 17尺 D. 15尺
5.如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A. 12cm2 B. 18cm2 C. 22cm2 D. 36cm2
6.如图,有一个圆柱,它的高等于12cm,底面上圆的周长等于18cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面与点A相对的点B处的食物,则蚂蚁沿圆柱侧面爬行的最短路程是( )
A. 15cm B. 17cm C. 18cm D. 30cm
7.《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高丈,末折抵地,问折者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子?( )
A. 4尺 B. 4.55尺 C. 5尺 D. 5.55尺
8.如图,一轮船以12海里/时的速度从港口A出发向东北方向航行,另一轮船以5海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后两船相距( )
A. 13 海里 B. 16 海里 C. 20 海里 D. 26 海里
9.如图, 中, , , , 是 边上的中线,则 的长度为( )
A. 1 B. 2 C. D.
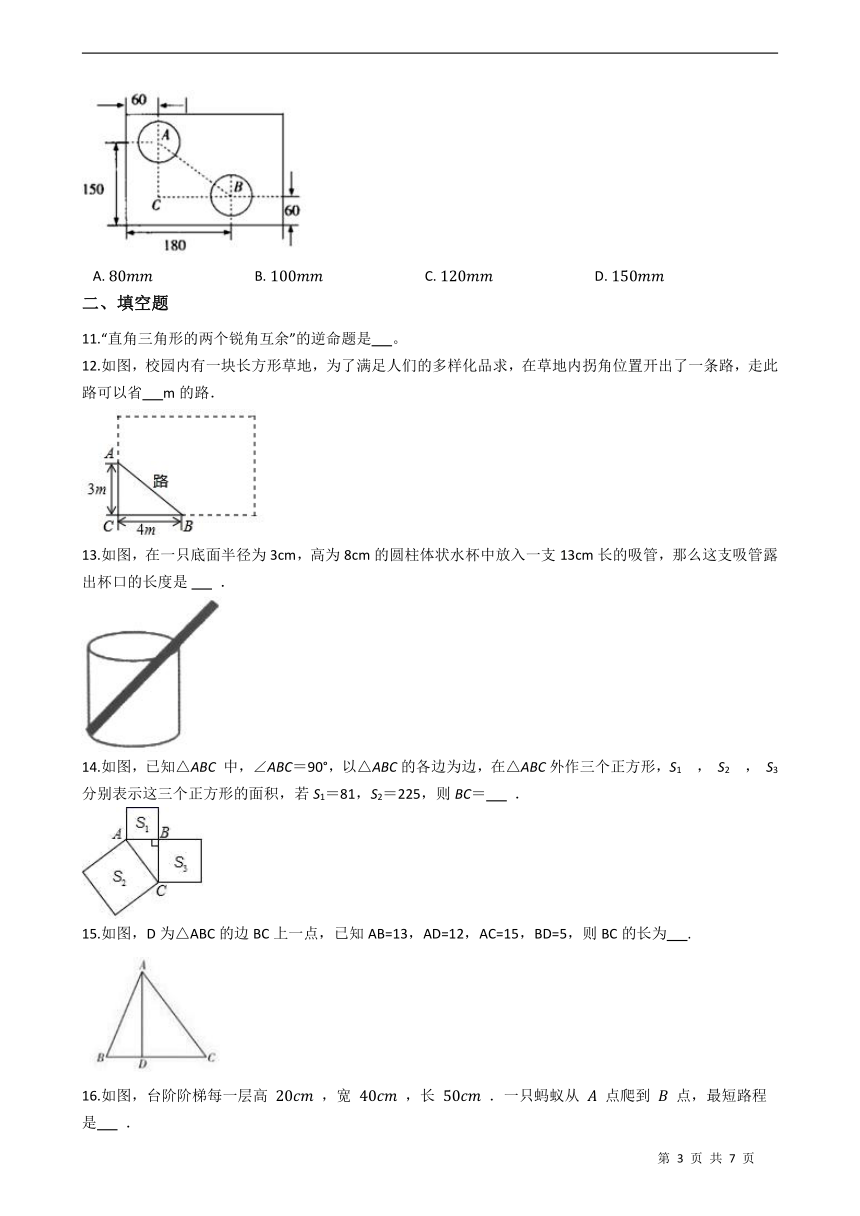
10.如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位: ),计算两圆孔中心A和B的距离为( )
A. B. C. D.
二、填空题
11.“直角三角形的两个锐角互余”的逆命题是 。
12.如图,校园内有一块长方形草地,为了满足人们的多样化品求,在草地内拐角位置开出了一条路,走此路可以省 m的路.
13.如图,在一只底面半径为3cm,高为8cm的圆柱体状水杯中放入一支13cm长的吸管,那么这支吸管露出杯口的长度是 .
14.如图,已知△ABC 中,∠ABC=90°,以△ABC的各边为边,在△ABC外作三个正方形,S1 , S2 , S3分别表示这三个正方形的面积,若S1=81,S2=225,则BC= .
15.如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为 .
16.如图,台阶阶梯每一层高 ,宽 ,长 .一只蚂蚁从 点爬到 点,最短路程是 .
三、解答题
17.如图,在边长为1的正方形组成的网格中,有AB,CD,EF,GH四条线段,端点都在格点上,你能选取其中三条线段组成一个直角三角形吗?请说明理由.
18.如图,一棵竖直生长的竹子高为8米,一阵强风将竹子从C处吹折,竹子的顶端A刚好触地,且与竹子底端的距离AB是4米.求竹子折断处与根部的距离CB.
19.如图所示,在操场上竖直立着一根长为2米的测影竿CD,早晨测得它的影长AD为4米,中午测得它的影长BD为1米,试判定△ABC的形状,并说明理由。
20.某小区有一块如图所示的四边形空地ABCD,为了庆祝建党百年,小区物业决定在这块空地上种植花草,测得已知 , , , , .种植花草的费用为80元 ,则该空地种植花草共需多少元?
21.如图,铁路上A,B两点相距25km,C,D为两村庄,于点A,于点B,若 , , 现要在AB上建一个周转站E,使得C,D两村到E站的距离相等,则周转站E应建在距A点多远处?
答案解析部分
一、单选题
1.【答案】 B
2.【答案】 D
3.【答案】 C
4.【答案】 C
5.【答案】 D
6.【答案】 A
7.【答案】 B
8.【答案】 D
9.【答案】 D
10.【答案】 D
二、填空题
11.【答案】 有两个(锐)角互余的三角形是直角三角形
12.【答案】 2
13.【答案】 3cm
14.【答案】 12
15.【答案】 14
16.【答案】
三、解答题
17.【答案】 解:能.由题意,得EF2=5,
CD2=20,
AB2=8,
GH2=13,
因为5+8=13,
所以EF2+AB2=GH2 ,
所以选取EF,AB,GH能组成直角三角形.
18.【答案】 解:由题意知BC+AC=8,∠CBA=90°,
∴设BC长为x米,则AC长为()米,
∴在Rt△CBA中,有 ,
即:x2+16=(8-x)2 ,
解得: ,
∴竹子折断处C与根部的距离CB为3米.
19.【答案】 解:△ABC是直角三角形.理由如下:
由题意,得CD⊥AB,CD=2,AD=4,BD=1,
所以BC2= BD2 +CD2=5,AC2=AD2 +CD2 =20,AB2=25,
所以BC2 +AC2=AB2 ,所以△ABC是直角三角形.
20.【答案】 解:连接AC,
∵ , , ,
∴ ,
又∵ , ,
∴ ,
∴ 是直角三角形, ,
∴ ,
∴种植花草共需 (元);
21.【答案】 解:设E点在距A点xkm处,
则AE长为xkm,BE长为km.
, 是直角三角形.
由勾股定理,得.
同理,在中, , 由题意,得 , 即..
,
解得.
答:E应建在距A点15km处.
(
第
7
页
共
7
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版数学八年级下册第十七章勾股定理的逆定理
一、单选题
1.下列各组数中,能构成直角三角形的是( )
A. 4,5,6 B. 1,1, C. 6,8,13 D. 5,12,15
2.△ABC的三边为a,b,c且(a+b)(a﹣b)=c2 , 则该三角形是( )
A. 锐角三角形 B. 以c为斜边的直角三角形
C. 以b为斜边的直角三角形 D. 以a为斜边的直角三角形
3.在如图所示的方格纸中,点A,B,C均为格点,则的度数是( )
A. B. C. D.
4.如图有一个水池,水面BE的宽为16尺,在水池的中央有一根芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个芦苇的高度是( )
A. 26尺 B. 24尺 C. 17尺 D. 15尺
5.如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积为( )
A. 12cm2 B. 18cm2 C. 22cm2 D. 36cm2
6.如图,有一个圆柱,它的高等于12cm,底面上圆的周长等于18cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面与点A相对的点B处的食物,则蚂蚁沿圆柱侧面爬行的最短路程是( )
A. 15cm B. 17cm C. 18cm D. 30cm
7.《九章算术》是我国古代数学的经典著作,书中有一个“折竹抵地”问题:“今有竹高丈,末折抵地,问折者高几何?”意思是:一根竹子,原来高一丈(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部三尺远,问:原处还有多高的竹子?( )
A. 4尺 B. 4.55尺 C. 5尺 D. 5.55尺
8.如图,一轮船以12海里/时的速度从港口A出发向东北方向航行,另一轮船以5海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后两船相距( )
A. 13 海里 B. 16 海里 C. 20 海里 D. 26 海里
9.如图, 中, , , , 是 边上的中线,则 的长度为( )
A. 1 B. 2 C. D.
10.如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位: ),计算两圆孔中心A和B的距离为( )
A. B. C. D.
二、填空题
11.“直角三角形的两个锐角互余”的逆命题是 。
12.如图,校园内有一块长方形草地,为了满足人们的多样化品求,在草地内拐角位置开出了一条路,走此路可以省 m的路.
13.如图,在一只底面半径为3cm,高为8cm的圆柱体状水杯中放入一支13cm长的吸管,那么这支吸管露出杯口的长度是 .
14.如图,已知△ABC 中,∠ABC=90°,以△ABC的各边为边,在△ABC外作三个正方形,S1 , S2 , S3分别表示这三个正方形的面积,若S1=81,S2=225,则BC= .
15.如图,D为△ABC的边BC上一点,已知AB=13,AD=12,AC=15,BD=5,则BC的长为 .
16.如图,台阶阶梯每一层高 ,宽 ,长 .一只蚂蚁从 点爬到 点,最短路程是 .
三、解答题
17.如图,在边长为1的正方形组成的网格中,有AB,CD,EF,GH四条线段,端点都在格点上,你能选取其中三条线段组成一个直角三角形吗?请说明理由.
18.如图,一棵竖直生长的竹子高为8米,一阵强风将竹子从C处吹折,竹子的顶端A刚好触地,且与竹子底端的距离AB是4米.求竹子折断处与根部的距离CB.
19.如图所示,在操场上竖直立着一根长为2米的测影竿CD,早晨测得它的影长AD为4米,中午测得它的影长BD为1米,试判定△ABC的形状,并说明理由。
20.某小区有一块如图所示的四边形空地ABCD,为了庆祝建党百年,小区物业决定在这块空地上种植花草,测得已知 , , , , .种植花草的费用为80元 ,则该空地种植花草共需多少元?
21.如图,铁路上A,B两点相距25km,C,D为两村庄,于点A,于点B,若 , , 现要在AB上建一个周转站E,使得C,D两村到E站的距离相等,则周转站E应建在距A点多远处?
答案解析部分
一、单选题
1.【答案】 B
2.【答案】 D
3.【答案】 C
4.【答案】 C
5.【答案】 D
6.【答案】 A
7.【答案】 B
8.【答案】 D
9.【答案】 D
10.【答案】 D
二、填空题
11.【答案】 有两个(锐)角互余的三角形是直角三角形
12.【答案】 2
13.【答案】 3cm
14.【答案】 12
15.【答案】 14
16.【答案】
三、解答题
17.【答案】 解:能.由题意,得EF2=5,
CD2=20,
AB2=8,
GH2=13,
因为5+8=13,
所以EF2+AB2=GH2 ,
所以选取EF,AB,GH能组成直角三角形.
18.【答案】 解:由题意知BC+AC=8,∠CBA=90°,
∴设BC长为x米,则AC长为()米,
∴在Rt△CBA中,有 ,
即:x2+16=(8-x)2 ,
解得: ,
∴竹子折断处C与根部的距离CB为3米.
19.【答案】 解:△ABC是直角三角形.理由如下:
由题意,得CD⊥AB,CD=2,AD=4,BD=1,
所以BC2= BD2 +CD2=5,AC2=AD2 +CD2 =20,AB2=25,
所以BC2 +AC2=AB2 ,所以△ABC是直角三角形.
20.【答案】 解:连接AC,
∵ , , ,
∴ ,
又∵ , ,
∴ ,
∴ 是直角三角形, ,
∴ ,
∴种植花草共需 (元);
21.【答案】 解:设E点在距A点xkm处,
则AE长为xkm,BE长为km.
, 是直角三角形.
由勾股定理,得.
同理,在中, , 由题意,得 , 即..
,
解得.
答:E应建在距A点15km处.
(
第
7
页
共
7
页
)
