人教版数学七年级下册5.3.1平行线的性质同步练习 (word版含答案)
文档属性
| 名称 | 人教版数学七年级下册5.3.1平行线的性质同步练习 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 95.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 07:53:52 | ||
图片预览


文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版数学七年级下册第五章第三节平行线的性质
一、单选题
1.一把直尺与一块直角三角板按如图方式摆放,若∠1=28°,则∠2=( )
A. 62° B. 58° C. 52° D. 48°
2.下列命题是假命题的是( )
A. 同旁内角互补,两直线平行;
B. 如果两条直线都和第三条直线平行,那么这两条直线也互相平行;
C. 同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行;
D. 同位角互补,两直线平行;
3.如图,直线AB∥CD,直线AB、CD被直线EF所截,交点分别为点M、点N,若∠AME=130°,则∠DNM的度数为( )
A. 30° B. 40° C. 50° D. 60°
4.将一副三角板按如图所示的位置摆放在直尺上,则的度数为( )
A. 60° B. 65° C. 70° D. 75°
5.直线、、、如图所示.若∠1=∠2,则下列结论错误的是( )
A. ABCD B. ∠EFB=∠3 C. ∠4=∠5 D. ∠3=∠5
6.如图,已知AD//BC,∠B=32°,DB平分∠ADE,则∠DEC=( )
A. 64° B. 66° C. 74° D. 86°
7.如图,在中,点D在边上, , 连接 . 若 , , 则 的大小为( )
A. B. C. D.
8.如图所示,已知CB∥DF,则下列结论中成立的是( )
A. ∠1=∠2 B. ∠1=∠3 C. ∠3=∠2 D. ∠1+∠2=90°
9.如图,将一块含有30°角的直角三角板的顶点放在直尺的一边上,若∠2=110°,则∠1的度数是( )
A. 10° B. 20° C. 30° D. 40°
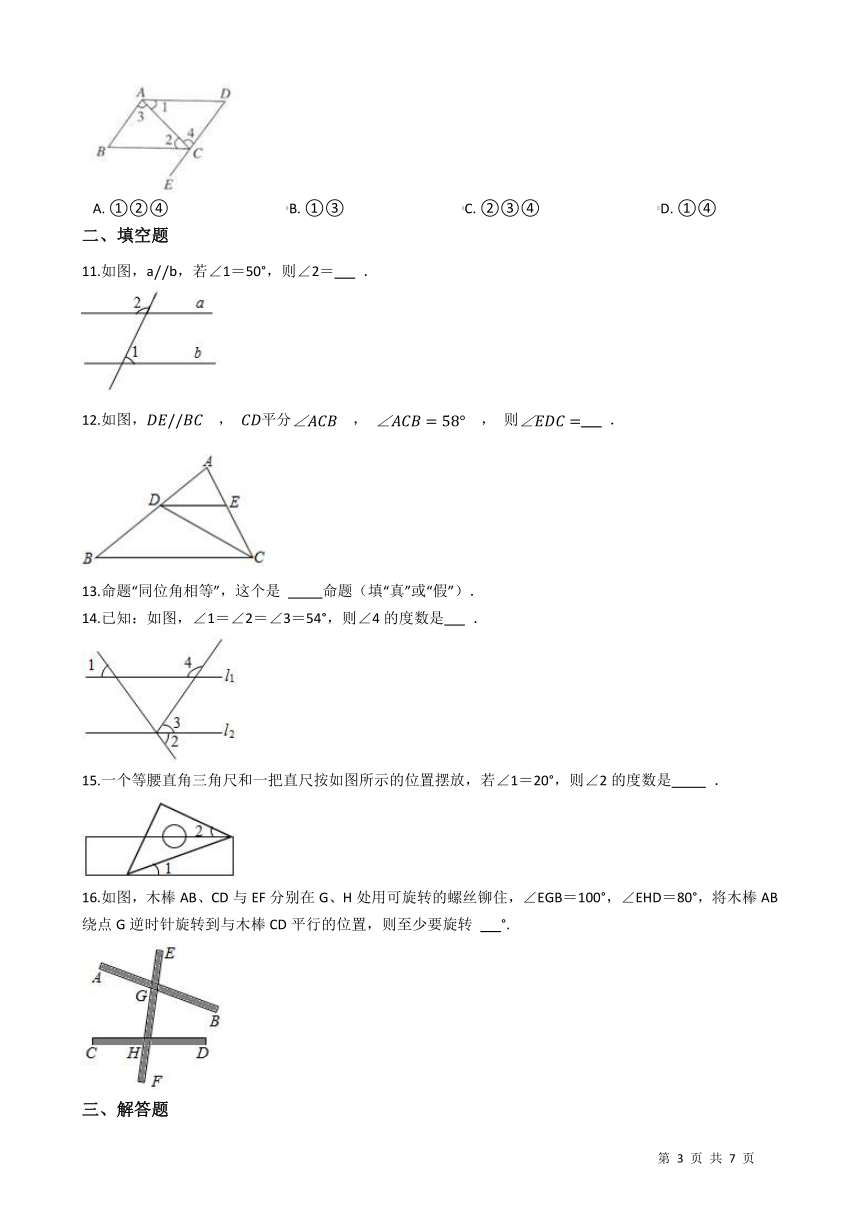
10.如图所示,下列条件:①∠1=∠2;②∠D+∠BAD=180°;③∠3=∠4;④∠BCE=∠D.一定能判定AD∥BC的条件是( )
A. ①②④ B. ①③ C. ②③④ D. ①④
二、填空题
11.如图,ab,若∠1=50°,则∠2= .
12.如图, , 平分 , , 则 .
13.命题“同位角相等”,这个是 命题(填“真”或“假”).
14.已知:如图,∠1=∠2=∠3=54°,则∠4的度数是 .
15.一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若∠1=20°,则∠2的度数是 .
16.如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 °.
三、解答题
17.已知如图, , , , , 求证:.
完成下面的证明过程:
证明:∵ ,
∴( )
∵ ▲ (已知)
∴.( )
∴.
∵ , (已知)
∴ ▲
又∵ ,
∴ ,
∴ , ( )
∴.( )
18.如图,已知DE∥BC,BE是∠ABC的平分线,∠C=70°,∠ABC=50°.求∠DEB和∠BEC的度数.
19.如图所示,直线AB∥CD,点E在AB上,EF交CD于点F,EG平分∠BEF,交CD于点G.若∠AEF=46°,求∠EGF的度数.
20.如图,GF∥CD,∠1=∠2.求证:∠CED+∠ACB=180°.
21.如图,已知AD⊥BC,FG⊥BC,垂足分别为点D,G,且∠1=∠2,猜想:∠BDE与∠C有怎样的数量关系?说明理由.
答案解析部分
一、单选题
1.【答案】 A
2.【答案】 D
3.【答案】 C
4.【答案】 D
5.【答案】 D
6.【答案】 A
7.【答案】 D
8.【答案】 C
9.【答案】 D
10.【答案】 D
二、填空题
11.【答案】 130°
12.【答案】 29°
13.【答案】 假
14.【答案】 126°
15.【答案】 25°
16.【答案】 20
三、解答题
17.【答案】 证明:∵∠AOB=80°,
∴∠COD=∠AOB=80°(对顶角相等).
∵BC∥EF(已知),
∴∠COD+∠1=180°(两直线平行,同旁内角互补).
∴∠1=100°.
∵∠1+∠C=160°(已知),
∴∠C=160°-∠1=60°.
又∵∠B=60°,
∴∠B=∠C.
∴AB∥CD(内错角相等,两直线平行).
∴∠A=∠D(两直线平行,内错角相等).
18.【答案】 解:∵ BE是∠ABC的平分线,∠ABC=50°,
∴∠1=∠2=25°.
∵ DE∥BC,
∴∠DEB =∠2=25°.
在△BEC中,∠C=70°,
∴∠BEC =180°-∠C-∠2=180°-70°-25°=85°.
19.【答案】 解:∵∠AEF+∠BEF= 180°(平角定义),∠AEF=46°(已知),
∴∠BEF= 180°-∠AEF= 180°-46°= 134°.
∵EG平分∠BEF(已知),
∴∠BEG=∠FEG= ∠BEF= ×134°=67°(角平分线的定义).
∵AB∥CD(已知),
∴∠EGF=∠BEG=67°(两直线平行,内错角相等).
20.【答案】 证明:∵GF∥CD,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴DE∥BC,
∴∠CED+∠ACB=180°.
21.【答案】 解:∠BDE=∠C.理由如下:
∵AD⊥BC,FG⊥BC(已知),
∴∠ADC=∠FGC=90°(垂直的定义),
∴AD∥FG(同位角相等,两直线平行),
∴∠1=∠3(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠3=∠2 (等量代换),
∴ED∥AC(内错角相等,两直线平行),
∴∠BDE=∠C(两直线平行,同位角相等).
(
第
1
页
共
7
页
)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
人教版数学七年级下册第五章第三节平行线的性质
一、单选题
1.一把直尺与一块直角三角板按如图方式摆放,若∠1=28°,则∠2=( )
A. 62° B. 58° C. 52° D. 48°
2.下列命题是假命题的是( )
A. 同旁内角互补,两直线平行;
B. 如果两条直线都和第三条直线平行,那么这两条直线也互相平行;
C. 同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行;
D. 同位角互补,两直线平行;
3.如图,直线AB∥CD,直线AB、CD被直线EF所截,交点分别为点M、点N,若∠AME=130°,则∠DNM的度数为( )
A. 30° B. 40° C. 50° D. 60°
4.将一副三角板按如图所示的位置摆放在直尺上,则的度数为( )
A. 60° B. 65° C. 70° D. 75°
5.直线、、、如图所示.若∠1=∠2,则下列结论错误的是( )
A. ABCD B. ∠EFB=∠3 C. ∠4=∠5 D. ∠3=∠5
6.如图,已知AD//BC,∠B=32°,DB平分∠ADE,则∠DEC=( )
A. 64° B. 66° C. 74° D. 86°
7.如图,在中,点D在边上, , 连接 . 若 , , 则 的大小为( )
A. B. C. D.
8.如图所示,已知CB∥DF,则下列结论中成立的是( )
A. ∠1=∠2 B. ∠1=∠3 C. ∠3=∠2 D. ∠1+∠2=90°
9.如图,将一块含有30°角的直角三角板的顶点放在直尺的一边上,若∠2=110°,则∠1的度数是( )
A. 10° B. 20° C. 30° D. 40°
10.如图所示,下列条件:①∠1=∠2;②∠D+∠BAD=180°;③∠3=∠4;④∠BCE=∠D.一定能判定AD∥BC的条件是( )
A. ①②④ B. ①③ C. ②③④ D. ①④
二、填空题
11.如图,ab,若∠1=50°,则∠2= .
12.如图, , 平分 , , 则 .
13.命题“同位角相等”,这个是 命题(填“真”或“假”).
14.已知:如图,∠1=∠2=∠3=54°,则∠4的度数是 .
15.一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若∠1=20°,则∠2的度数是 .
16.如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 °.
三、解答题
17.已知如图, , , , , 求证:.
完成下面的证明过程:
证明:∵ ,
∴( )
∵ ▲ (已知)
∴.( )
∴.
∵ , (已知)
∴ ▲
又∵ ,
∴ ,
∴ , ( )
∴.( )
18.如图,已知DE∥BC,BE是∠ABC的平分线,∠C=70°,∠ABC=50°.求∠DEB和∠BEC的度数.
19.如图所示,直线AB∥CD,点E在AB上,EF交CD于点F,EG平分∠BEF,交CD于点G.若∠AEF=46°,求∠EGF的度数.
20.如图,GF∥CD,∠1=∠2.求证:∠CED+∠ACB=180°.
21.如图,已知AD⊥BC,FG⊥BC,垂足分别为点D,G,且∠1=∠2,猜想:∠BDE与∠C有怎样的数量关系?说明理由.
答案解析部分
一、单选题
1.【答案】 A
2.【答案】 D
3.【答案】 C
4.【答案】 D
5.【答案】 D
6.【答案】 A
7.【答案】 D
8.【答案】 C
9.【答案】 D
10.【答案】 D
二、填空题
11.【答案】 130°
12.【答案】 29°
13.【答案】 假
14.【答案】 126°
15.【答案】 25°
16.【答案】 20
三、解答题
17.【答案】 证明:∵∠AOB=80°,
∴∠COD=∠AOB=80°(对顶角相等).
∵BC∥EF(已知),
∴∠COD+∠1=180°(两直线平行,同旁内角互补).
∴∠1=100°.
∵∠1+∠C=160°(已知),
∴∠C=160°-∠1=60°.
又∵∠B=60°,
∴∠B=∠C.
∴AB∥CD(内错角相等,两直线平行).
∴∠A=∠D(两直线平行,内错角相等).
18.【答案】 解:∵ BE是∠ABC的平分线,∠ABC=50°,
∴∠1=∠2=25°.
∵ DE∥BC,
∴∠DEB =∠2=25°.
在△BEC中,∠C=70°,
∴∠BEC =180°-∠C-∠2=180°-70°-25°=85°.
19.【答案】 解:∵∠AEF+∠BEF= 180°(平角定义),∠AEF=46°(已知),
∴∠BEF= 180°-∠AEF= 180°-46°= 134°.
∵EG平分∠BEF(已知),
∴∠BEG=∠FEG= ∠BEF= ×134°=67°(角平分线的定义).
∵AB∥CD(已知),
∴∠EGF=∠BEG=67°(两直线平行,内错角相等).
20.【答案】 证明:∵GF∥CD,
∴∠2=∠DCB,
∵∠1=∠2,
∴∠1=∠DCB,
∴DE∥BC,
∴∠CED+∠ACB=180°.
21.【答案】 解:∠BDE=∠C.理由如下:
∵AD⊥BC,FG⊥BC(已知),
∴∠ADC=∠FGC=90°(垂直的定义),
∴AD∥FG(同位角相等,两直线平行),
∴∠1=∠3(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠3=∠2 (等量代换),
∴ED∥AC(内错角相等,两直线平行),
∴∠BDE=∠C(两直线平行,同位角相等).
(
第
1
页
共
7
页
)
