1.3带电粒子在匀强磁场中的运动课件(共32张PPT)
文档属性
| 名称 | 1.3带电粒子在匀强磁场中的运动课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-02-27 14:54:42 | ||
图片预览









文档简介
(共32张PPT)
人教版选择性必修二
第一章 安培力与洛伦兹力
1.3带电粒子在匀强磁场中的运动
复习:
1、洛伦兹力产生的条件?
2、洛伦兹力的大小和方向如何确定?
3、洛伦兹力有什么特点?
射入匀强磁场中的带电粒子将做怎样的运动呢?
思考:
3、某些带电体是否考虑重力,要根据题目暗示或运动状态来判定
磁场中的带电粒子一般可分为两类:
1、带电的基本粒子:如电子,质子,α粒子,正负离子等。这些粒子所受重力和洛仑兹力相比在小得多,除非有说明或明确的暗示以外,一般都不考虑重力。(但并不能忽略质量)。
2、带电微粒:如带电小球、液滴、尘埃等。除非有说明或明确的暗示以外,一般都考虑重力。
一、带电粒子在匀强磁场中的运动
带电粒子平行射入匀强磁场的运动状态,? (重力不计)
问题1:
匀速直线运动
1、vllB
一、带电粒子在匀强磁场中的运动
问题2:
带电粒子垂直射入匀强磁场的运动状态? (重力不计)
1、vllB 匀速直线运动
V
-
F洛
V
-
F洛
V
-
F洛
V
-
F洛
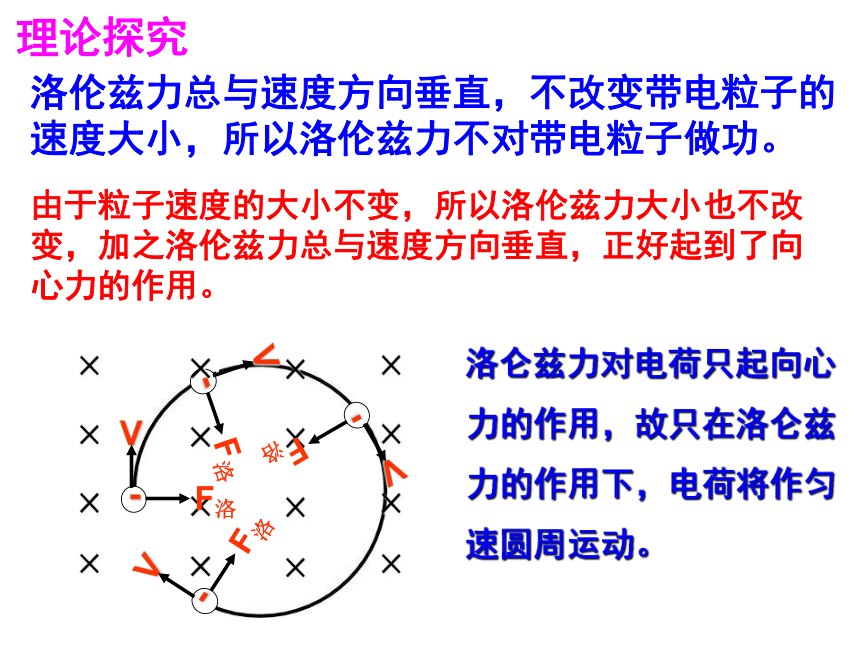
洛仑兹力对电荷只起向心力的作用,故只在洛仑兹力的作用下,电荷将作匀速圆周运动。
理论探究
洛伦兹力总与速度方向垂直,不改变带电粒子的速度大小,所以洛伦兹力不对带电粒子做功。
由于粒子速度的大小不变,所以洛伦兹力大小也不改变,加之洛伦兹力总与速度方向垂直,正好起到了向心力的作用。
一、带电粒子在匀强磁场中的运动
2、
沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁场中做匀速圆周运动
问题3:
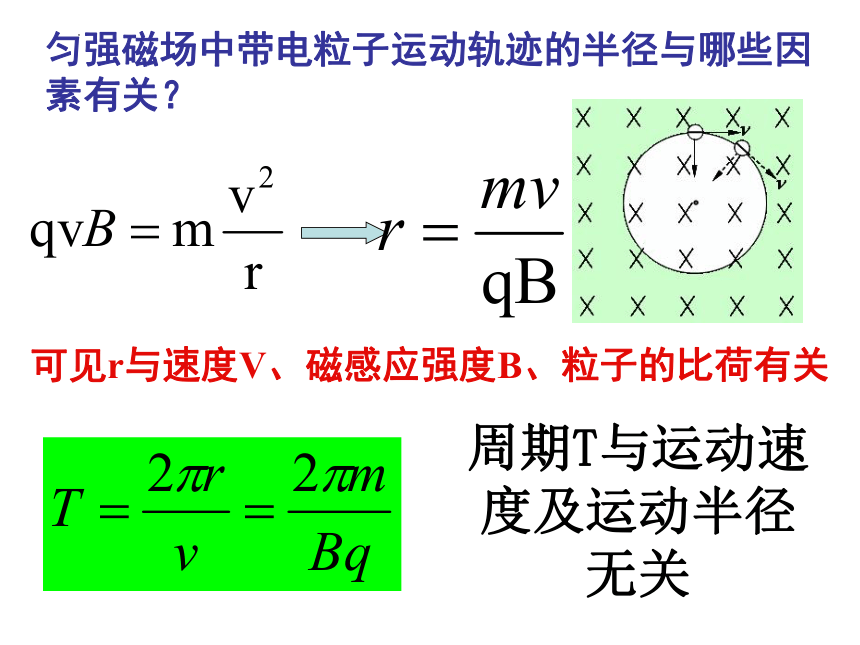
推导粒子在匀强磁场中做匀速圆周运动的圆半径r和运动周期T,与粒子的速度v和磁场的磁感应强度B的关系表达式
匀强磁场中带电粒子运动轨迹的半径与哪些因素有关?
可见r与速度V、磁感应强度B、粒子的比荷有关
周期T与运动速度及运动半径无关
励磁线圈
电 子 枪
磁场强弱选择挡
加速电压选择挡
洛伦兹力演示器
实验验证:
作用是改变电子束出射的速度
作用是能在两线圈之间产生平行于两线圈中心的连线的匀强磁场
带电粒子在匀强磁场中的偏转运动的实验.asf
观察1:不加磁场时电子束轨迹
观察4:若加逆时针的励磁电流,磁场方向如何,电子偏转方向将如何?
观察2:若加顺时针的励磁电流,磁场方向如何,电子偏转方向将如何?
观察3:改变加速电压和励磁电流时,电子束轨迹半径有何变化?如何解释?
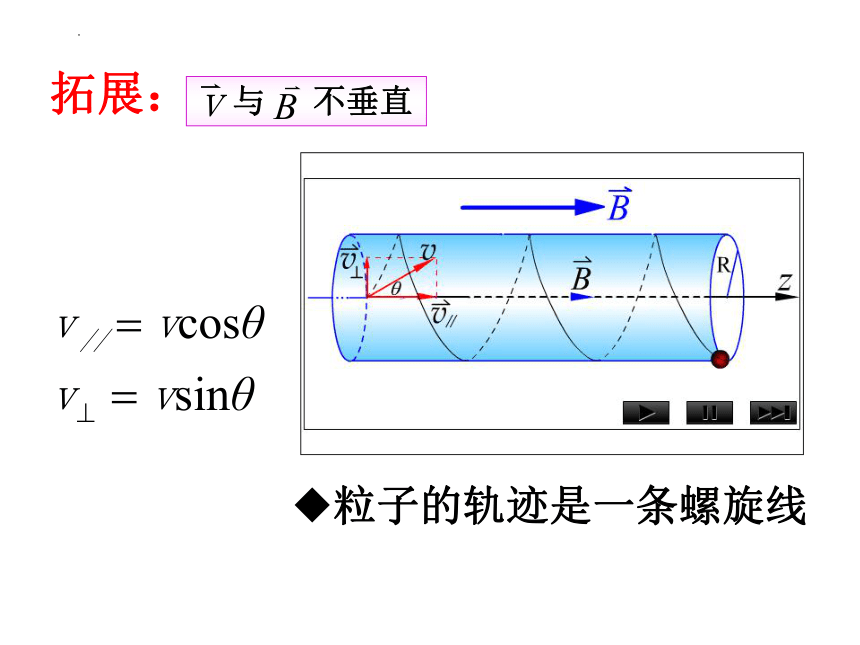
与 不垂直
拓展:
粒子的轨迹是一条螺旋线
通过威尔逊云室显示的正负电子在匀强磁场中的运动径迹
“气泡室”照片
1.不同带电粒子的径迹半径为什么不一样?
2.同一条径迹上为什么曲率半径会越来越小呢?
例1:一个带电粒子,沿垂直于磁场的方向射入一匀强磁场.粒子的一段径迹如下图所示.径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(带电量不变).从图中情况可以确定
A.粒子从a到b,带正电
B.粒子从a到b,带负电
C.粒子从b到a,带正电
D.粒子从b到a,带负电
C
带电粒子沿垂直电场或磁场射入场运动比较
电 场 磁 场
受力特点
运动性质
处理方法
F=qE大小、方向不变的恒力
F=qvB大小不变、F⊥v、不做功
匀变速曲线运动
变加速曲线运动
同平抛运动
圆周运动处理
例题2:一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上(如图)
(1)求粒子进入磁场
时的速率。
(2)求粒子在磁场中
运动的轨道半径。
测量带电粒子的质量或比荷
分析同位素
(一)、质谱仪:
1、质谱仪是测量带电粒子质量或比荷、分析同位素
2、基本原理
将质量不等、电荷数相等的带电粒子经同一电场加速再垂直进入同一匀强磁场,由于粒子速度不同,引起轨迹半径不同而分开,进而分析某元素中所含同位素的种类
3、推导
二、实际应用
质谱仪原理.swf
(二、)回旋加速器
1、直线加速器
原理:利用加速电场对带电粒子做正功使带电粒子的动能增加qU=Ek
由动能定理得带电粒子经几级的电场加速后增加的动能为Ek=( )q
直线加速器1wl1.swf
直线加速器2WL.swf
思考:
若需要很大的动能的粒子,利用直线加速器是否方便?为什么?那应该怎么办?
2、回旋加速器
(1)构造
(2)工作原理
回旋加速器演示.swf
(二)、回旋加速器
1、作用:产生高速运动的粒子
2、原理
1)、两D形盒中有匀强磁场无电场,盒间缝隙有交变电场。
2)、交变电场的周期等于粒子做匀速圆周运动的周期。
3)、粒子最后出加速器的速度大小由盒的半径决定。
已知回旋加速器中D形盒内匀强磁场的磁感应强度大小为B,D形盒的半径为r.今将质量为m、电量为q的质子从间隙中心处由静止释放,求粒子在加速器内加速后所能达到的最大速度表达式.
3、注意
1、带电粒子在匀强磁场中的运动周期 跟运动速率和轨道半径无关,对于一定的带电粒子和一定的磁感应强度来说,这个周期是恒定的。
2、交变电场的往复变化周期和粒子的运动周期T相同,这样就可以保证粒子在每次经过交变电场时都被加速。
如果尽量增强回旋加速器的磁场或加大D形盒半径,我们是不是就可以使带电粒子获得任意高的能量吗?
3、由于侠义相对论的限制,回旋加速器只能把粒子加速到一定的能量。
回旋加速器中磁场的磁感应强度为B,D形盒的半径为R,用该回旋加速器加速质量为m、电量为q的粒子,设粒子加速前的初速度为零。求:
(1) 粒子的回转周期是多大?
(2)高频电极的周期为多大?
(3) 粒子的最大动能是多大?
3、带电粒子的最终能量
当带电粒子的速度最大时,其在磁场中的转动半径也最大,由r=mv/qB知道v=qBr/m
若D形盒的半径为R时,带电粒子的出射速度变为v=qBR/m
所以,带电粒子的最终动能为
所以,要提高加速粒子的最终能量,就应该尽可能的加大B的强度和D形盒的半径R
V
V
三、带电粒子做圆周运动的分析方法
(一)几个重要的几何关系:四点三角两(三角)形一根线(半径):
A
v
v
O’
α
B
θ
θ
θ‘
Φ(偏向角)
粒子速度的偏向角φ等与圆心角α,并等于AB弦与切线的夹角θ(弦切角)的2倍.即φ=α=2θ
V
V
V
V
带电粒子做圆周运动的分析方法
带电粒子做圆周运动的分析方法
(二)解题步骤:画轨、定心、求半径
1.定心方法:
(1)两径定心:已知入射方向和出射方向, 与速度垂直的半径交点就是圆弧轨道的圆心。
(2)一径一弦定心:已知入射方向和出射点的位置时,半径与弦中垂线的交点就是圆弧轨道的圆心。
V
P
M
O
V0
P
M
O
V
带电粒子做圆周运动的分析方法
2、求半径: 一般利用几何知识,常用解三角形的方法。
(4)确定运动时间:利用圆心角与弦切角的关系,或者是四边形内角和等于 计算出圆心角的大小,由公式可求出运动时间。
d
B
e
θ
v
练习1。如图所示,一束电子(电量为e)以速度V垂直射入磁感应强度为B、宽度为d的匀强磁场,穿透磁场时的速度与电子原来的入射方向的夹角为300。求 : (1) 电子的质量m= (2) 电子在磁场中的运动时间t=
d
B
e
θ
v
练习2.如图所示,在半径为R 的圆的范围内,有匀强磁场,方向垂直圆所在平面向里.一带负电的质量为m电量为q粒子,从A点沿半径AO的方向射入,并从C点射出磁场.∠AOC=120o.则此粒子在磁场中运行的时间t=__________.(不计重力).
A
B
R
v
v
O
120°
C
A
B
R
v
v
O
120°
C
人教版选择性必修二
第一章 安培力与洛伦兹力
1.3带电粒子在匀强磁场中的运动
复习:
1、洛伦兹力产生的条件?
2、洛伦兹力的大小和方向如何确定?
3、洛伦兹力有什么特点?
射入匀强磁场中的带电粒子将做怎样的运动呢?
思考:
3、某些带电体是否考虑重力,要根据题目暗示或运动状态来判定
磁场中的带电粒子一般可分为两类:
1、带电的基本粒子:如电子,质子,α粒子,正负离子等。这些粒子所受重力和洛仑兹力相比在小得多,除非有说明或明确的暗示以外,一般都不考虑重力。(但并不能忽略质量)。
2、带电微粒:如带电小球、液滴、尘埃等。除非有说明或明确的暗示以外,一般都考虑重力。
一、带电粒子在匀强磁场中的运动
带电粒子平行射入匀强磁场的运动状态,? (重力不计)
问题1:
匀速直线运动
1、vllB
一、带电粒子在匀强磁场中的运动
问题2:
带电粒子垂直射入匀强磁场的运动状态? (重力不计)
1、vllB 匀速直线运动
V
-
F洛
V
-
F洛
V
-
F洛
V
-
F洛
洛仑兹力对电荷只起向心力的作用,故只在洛仑兹力的作用下,电荷将作匀速圆周运动。
理论探究
洛伦兹力总与速度方向垂直,不改变带电粒子的速度大小,所以洛伦兹力不对带电粒子做功。
由于粒子速度的大小不变,所以洛伦兹力大小也不改变,加之洛伦兹力总与速度方向垂直,正好起到了向心力的作用。
一、带电粒子在匀强磁场中的运动
2、
沿着与磁场垂直的方向射入磁场的带电粒子,在匀强磁场中做匀速圆周运动
问题3:
推导粒子在匀强磁场中做匀速圆周运动的圆半径r和运动周期T,与粒子的速度v和磁场的磁感应强度B的关系表达式
匀强磁场中带电粒子运动轨迹的半径与哪些因素有关?
可见r与速度V、磁感应强度B、粒子的比荷有关
周期T与运动速度及运动半径无关
励磁线圈
电 子 枪
磁场强弱选择挡
加速电压选择挡
洛伦兹力演示器
实验验证:
作用是改变电子束出射的速度
作用是能在两线圈之间产生平行于两线圈中心的连线的匀强磁场
带电粒子在匀强磁场中的偏转运动的实验.asf
观察1:不加磁场时电子束轨迹
观察4:若加逆时针的励磁电流,磁场方向如何,电子偏转方向将如何?
观察2:若加顺时针的励磁电流,磁场方向如何,电子偏转方向将如何?
观察3:改变加速电压和励磁电流时,电子束轨迹半径有何变化?如何解释?
与 不垂直
拓展:
粒子的轨迹是一条螺旋线
通过威尔逊云室显示的正负电子在匀强磁场中的运动径迹
“气泡室”照片
1.不同带电粒子的径迹半径为什么不一样?
2.同一条径迹上为什么曲率半径会越来越小呢?
例1:一个带电粒子,沿垂直于磁场的方向射入一匀强磁场.粒子的一段径迹如下图所示.径迹上的每一小段都可近似看成圆弧.由于带电粒子使沿途的空气电离,粒子的能量逐渐减小(带电量不变).从图中情况可以确定
A.粒子从a到b,带正电
B.粒子从a到b,带负电
C.粒子从b到a,带正电
D.粒子从b到a,带负电
C
带电粒子沿垂直电场或磁场射入场运动比较
电 场 磁 场
受力特点
运动性质
处理方法
F=qE大小、方向不变的恒力
F=qvB大小不变、F⊥v、不做功
匀变速曲线运动
变加速曲线运动
同平抛运动
圆周运动处理
例题2:一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上(如图)
(1)求粒子进入磁场
时的速率。
(2)求粒子在磁场中
运动的轨道半径。
测量带电粒子的质量或比荷
分析同位素
(一)、质谱仪:
1、质谱仪是测量带电粒子质量或比荷、分析同位素
2、基本原理
将质量不等、电荷数相等的带电粒子经同一电场加速再垂直进入同一匀强磁场,由于粒子速度不同,引起轨迹半径不同而分开,进而分析某元素中所含同位素的种类
3、推导
二、实际应用
质谱仪原理.swf
(二、)回旋加速器
1、直线加速器
原理:利用加速电场对带电粒子做正功使带电粒子的动能增加qU=Ek
由动能定理得带电粒子经几级的电场加速后增加的动能为Ek=( )q
直线加速器1wl1.swf
直线加速器2WL.swf
思考:
若需要很大的动能的粒子,利用直线加速器是否方便?为什么?那应该怎么办?
2、回旋加速器
(1)构造
(2)工作原理
回旋加速器演示.swf
(二)、回旋加速器
1、作用:产生高速运动的粒子
2、原理
1)、两D形盒中有匀强磁场无电场,盒间缝隙有交变电场。
2)、交变电场的周期等于粒子做匀速圆周运动的周期。
3)、粒子最后出加速器的速度大小由盒的半径决定。
已知回旋加速器中D形盒内匀强磁场的磁感应强度大小为B,D形盒的半径为r.今将质量为m、电量为q的质子从间隙中心处由静止释放,求粒子在加速器内加速后所能达到的最大速度表达式.
3、注意
1、带电粒子在匀强磁场中的运动周期 跟运动速率和轨道半径无关,对于一定的带电粒子和一定的磁感应强度来说,这个周期是恒定的。
2、交变电场的往复变化周期和粒子的运动周期T相同,这样就可以保证粒子在每次经过交变电场时都被加速。
如果尽量增强回旋加速器的磁场或加大D形盒半径,我们是不是就可以使带电粒子获得任意高的能量吗?
3、由于侠义相对论的限制,回旋加速器只能把粒子加速到一定的能量。
回旋加速器中磁场的磁感应强度为B,D形盒的半径为R,用该回旋加速器加速质量为m、电量为q的粒子,设粒子加速前的初速度为零。求:
(1) 粒子的回转周期是多大?
(2)高频电极的周期为多大?
(3) 粒子的最大动能是多大?
3、带电粒子的最终能量
当带电粒子的速度最大时,其在磁场中的转动半径也最大,由r=mv/qB知道v=qBr/m
若D形盒的半径为R时,带电粒子的出射速度变为v=qBR/m
所以,带电粒子的最终动能为
所以,要提高加速粒子的最终能量,就应该尽可能的加大B的强度和D形盒的半径R
V
V
三、带电粒子做圆周运动的分析方法
(一)几个重要的几何关系:四点三角两(三角)形一根线(半径):
A
v
v
O’
α
B
θ
θ
θ‘
Φ(偏向角)
粒子速度的偏向角φ等与圆心角α,并等于AB弦与切线的夹角θ(弦切角)的2倍.即φ=α=2θ
V
V
V
V
带电粒子做圆周运动的分析方法
带电粒子做圆周运动的分析方法
(二)解题步骤:画轨、定心、求半径
1.定心方法:
(1)两径定心:已知入射方向和出射方向, 与速度垂直的半径交点就是圆弧轨道的圆心。
(2)一径一弦定心:已知入射方向和出射点的位置时,半径与弦中垂线的交点就是圆弧轨道的圆心。
V
P
M
O
V0
P
M
O
V
带电粒子做圆周运动的分析方法
2、求半径: 一般利用几何知识,常用解三角形的方法。
(4)确定运动时间:利用圆心角与弦切角的关系,或者是四边形内角和等于 计算出圆心角的大小,由公式可求出运动时间。
d
B
e
θ
v
练习1。如图所示,一束电子(电量为e)以速度V垂直射入磁感应强度为B、宽度为d的匀强磁场,穿透磁场时的速度与电子原来的入射方向的夹角为300。求 : (1) 电子的质量m= (2) 电子在磁场中的运动时间t=
d
B
e
θ
v
练习2.如图所示,在半径为R 的圆的范围内,有匀强磁场,方向垂直圆所在平面向里.一带负电的质量为m电量为q粒子,从A点沿半径AO的方向射入,并从C点射出磁场.∠AOC=120o.则此粒子在磁场中运行的时间t=__________.(不计重力).
A
B
R
v
v
O
120°
C
A
B
R
v
v
O
120°
C
