苏科版七年级数学下册 7.2 探索平行线的性质 课件(共18张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 7.2 探索平行线的性质 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 559.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 15:23:40 | ||
图片预览





文档简介
(共18张PPT)
探索平行线的性质
小明沿正北方向走到A点,向左转50 行进到B点,为了保证继续行进的方向与开始时平行,小明应向哪个方向转多少度?
情境导入:
小明向右转50 或者向左转130 .
平行线的判定方法有哪三种?它
们是先知道什么……后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
回顾
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
既然同学们知道两条平行线被第三条直线所截,
同位角相等,那么两条平行线被第三条直线所截,
内错角、同旁内角各有什么关系呢?
回顾
设问
A
B
P
C
D
E
F
2
1
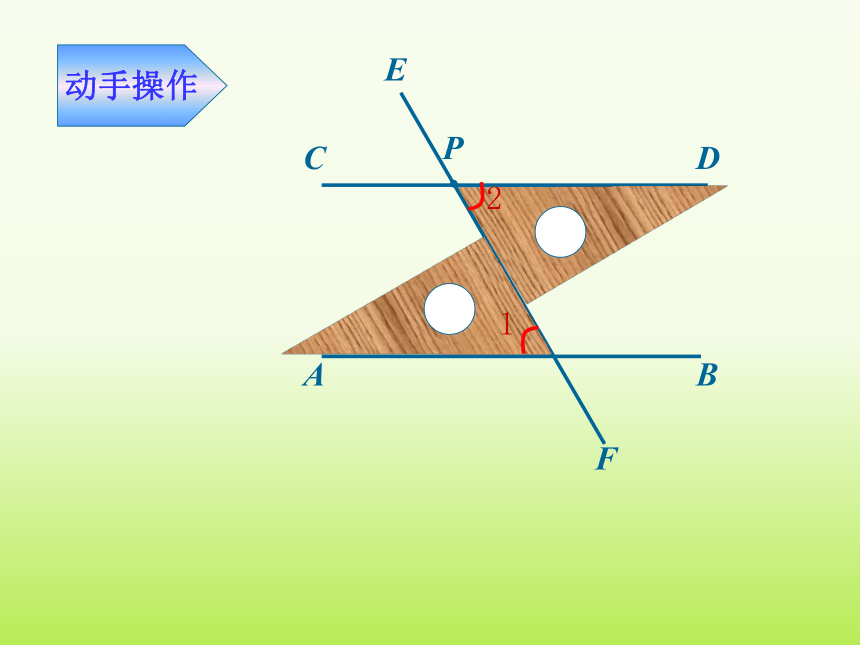
动手操作
1
2
3
a
b
实践探索
如图,已知:a∥b 那么 3与 2有什么关系?
平行线的性质2
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
结论
解:∵a∥b,
∴∠1=∠2,
又 ∵∠1=∠3,
∴∠2=∠3.
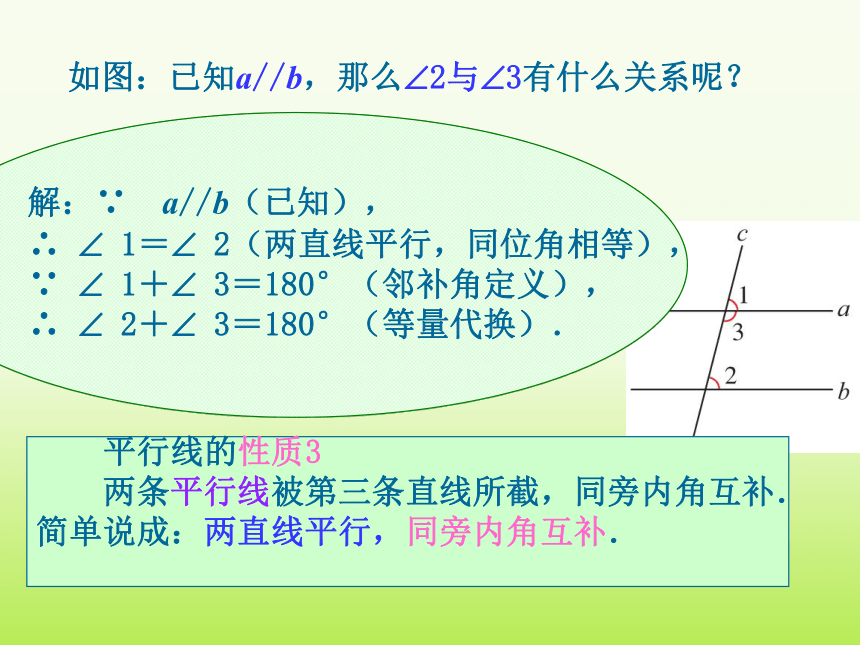
解:∵ a//b(已知),
∴ 1= 2(两直线平行,同位角相等),
∵ 1+ 3=180°(邻补角定义),
∴ 2+ 3=180°(等量代换).
如图:已知a//b,那么 2与 3有什么关系呢?
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
平行线的性质2
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
精彩回放
解:∵AD//BC (已知),
∴ A+ B=180°,
(两直线平行,同旁内角互补)
即 B=180 °- A=180 °-115 °=65 °,
∵AD//BC(已知) ,
∴ D+ C=180 °,
(两直线平行,同旁内角互补)
即 C=180 °- D=180 °-100 °=80 °.
答:梯形的另外两个角分别为65 °、80 °.
例1
C
B
A
D
如图是梯形有上底的一部分.已经量得 A=115°,
D=100°,梯形另外两个角各是多少度?
例2 如图,AD∥BC,∠A=∠C.试说明AB∥CD.
解 ∵ AD∥BC,
∴∠C=∠CDE(两直线平行,内错角相等),
又∵∠A=∠C,
∴∠A=∠CDE,
∴AB∥CD(同位角相等,两直线平行).
4
3
2
1
A
C
B
D
E
解:(1)∵AB∥CD
(已知) ,
∴∠1=∠2
(两直线平行,内错角相等) ,
又∵∠1=110°
∴∠1=∠2=110°
(已知),
(等量代换).
(2)∵AB∥CD
(已知) ,
∴∠1=∠3
(两直线平行,同位角相等) ,
又∵∠1=110°
∴∠1=∠3=110°
(已知),
(等量代换).
(3)∵AB∥CD
(已知) ,
∴∠1+∠4=180°
(两直线平行,同旁内角互补),
又∵∠1=110°
(已知),
∴110 °+∠4=180°
(等量代换),
∴∠4=180°-110°=70°
(等式性质).
例3 如图,已知AB∥CD,∠1=110 ,你能求出∠2、∠3、∠4的度数吗?
平行线的“判定”与“性质”有什么不同.
比一比
已知角之间的关系(相等或互补),得到两直线
平行的结论是平行线的判定.
已知两直线平行,得到角之间的关系(相等或互
补)的结论是平行线的性质.
2
1
D
C
B
A
填空:
如图:∵∠1=∠2(已知),
∴AD∥BC( 内错角相等,两直线平行 ),
∴∠BCD+∠D=180°(两直线平行,同旁内角互补) .
E
D
C
B
A
(已知) ,
解(1)∵∠BDE=60 ° ∠B=60°
∴∠BDE+∠B=180
(等式性质) ,
∴DE∥BC
(同旁内角互补,两直线平行) .
(2)∵ DE∥BC
(已证),
∴∠CED+∠C=180
(两直线平行,同旁内角互补) ,
又∵∠C=40°
(已知) ,
(等式性质) .
∴∠CED=180 -40 =140
例4 如图,在△ABC中,
(1)若∠BDE=120 ,∠B=60 .请说明DE∥BC.
(2)若DE∥BC,且∠C=40 .求∠CED的度数.
1.如图,AB、CD被EF所截,AB//CD.
按要求填空:
若∠1=120°,则∠2=____( );
∠3=___- ∠1=__°( )
120 °
180°
60
两直线平行,内错角相等.
两直线平行,同旁内角互补.
2.如图,已知AB//CD,AD//BC.填空:
(1)∵ AB//CD (已知),
∴ ∠1= ∠___
( );
(2) ∵ AD//BC (已知)
∴ ∠2= ∠ ( ).
两直线平行,内错角相等.
两直线平行,内错角相等.
D
ACB
3. 如图,已知AB∥CD,AD∥BC.判断∠1与∠2是否相等,并说明理由.
∵AB∥CD,
∴∠2=∠BCE(两直线平行,内错角相等),
∵AD∥BC,
∴∠1=∠BCE(两直线平行,同位角相等),
∴∠1=∠2.
解
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结:
探索平行线的性质
小明沿正北方向走到A点,向左转50 行进到B点,为了保证继续行进的方向与开始时平行,小明应向哪个方向转多少度?
情境导入:
小明向右转50 或者向左转130 .
平行线的判定方法有哪三种?它
们是先知道什么……后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
回顾
如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?
既然同学们知道两条平行线被第三条直线所截,
同位角相等,那么两条平行线被第三条直线所截,
内错角、同旁内角各有什么关系呢?
回顾
设问
A
B
P
C
D
E
F
2
1
动手操作
1
2
3
a
b
实践探索
如图,已知:a∥b 那么 3与 2有什么关系?
平行线的性质2
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
结论
解:∵a∥b,
∴∠1=∠2,
又 ∵∠1=∠3,
∴∠2=∠3.
解:∵ a//b(已知),
∴ 1= 2(两直线平行,同位角相等),
∵ 1+ 3=180°(邻补角定义),
∴ 2+ 3=180°(等量代换).
如图:已知a//b,那么 2与 3有什么关系呢?
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
平行线的性质2
两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
平行线的性质3
两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
精彩回放
解:∵AD//BC (已知),
∴ A+ B=180°,
(两直线平行,同旁内角互补)
即 B=180 °- A=180 °-115 °=65 °,
∵AD//BC(已知) ,
∴ D+ C=180 °,
(两直线平行,同旁内角互补)
即 C=180 °- D=180 °-100 °=80 °.
答:梯形的另外两个角分别为65 °、80 °.
例1
C
B
A
D
如图是梯形有上底的一部分.已经量得 A=115°,
D=100°,梯形另外两个角各是多少度?
例2 如图,AD∥BC,∠A=∠C.试说明AB∥CD.
解 ∵ AD∥BC,
∴∠C=∠CDE(两直线平行,内错角相等),
又∵∠A=∠C,
∴∠A=∠CDE,
∴AB∥CD(同位角相等,两直线平行).
4
3
2
1
A
C
B
D
E
解:(1)∵AB∥CD
(已知) ,
∴∠1=∠2
(两直线平行,内错角相等) ,
又∵∠1=110°
∴∠1=∠2=110°
(已知),
(等量代换).
(2)∵AB∥CD
(已知) ,
∴∠1=∠3
(两直线平行,同位角相等) ,
又∵∠1=110°
∴∠1=∠3=110°
(已知),
(等量代换).
(3)∵AB∥CD
(已知) ,
∴∠1+∠4=180°
(两直线平行,同旁内角互补),
又∵∠1=110°
(已知),
∴110 °+∠4=180°
(等量代换),
∴∠4=180°-110°=70°
(等式性质).
例3 如图,已知AB∥CD,∠1=110 ,你能求出∠2、∠3、∠4的度数吗?
平行线的“判定”与“性质”有什么不同.
比一比
已知角之间的关系(相等或互补),得到两直线
平行的结论是平行线的判定.
已知两直线平行,得到角之间的关系(相等或互
补)的结论是平行线的性质.
2
1
D
C
B
A
填空:
如图:∵∠1=∠2(已知),
∴AD∥BC( 内错角相等,两直线平行 ),
∴∠BCD+∠D=180°(两直线平行,同旁内角互补) .
E
D
C
B
A
(已知) ,
解(1)∵∠BDE=60 ° ∠B=60°
∴∠BDE+∠B=180
(等式性质) ,
∴DE∥BC
(同旁内角互补,两直线平行) .
(2)∵ DE∥BC
(已证),
∴∠CED+∠C=180
(两直线平行,同旁内角互补) ,
又∵∠C=40°
(已知) ,
(等式性质) .
∴∠CED=180 -40 =140
例4 如图,在△ABC中,
(1)若∠BDE=120 ,∠B=60 .请说明DE∥BC.
(2)若DE∥BC,且∠C=40 .求∠CED的度数.
1.如图,AB、CD被EF所截,AB//CD.
按要求填空:
若∠1=120°,则∠2=____( );
∠3=___- ∠1=__°( )
120 °
180°
60
两直线平行,内错角相等.
两直线平行,同旁内角互补.
2.如图,已知AB//CD,AD//BC.填空:
(1)∵ AB//CD (已知),
∴ ∠1= ∠___
( );
(2) ∵ AD//BC (已知)
∴ ∠2= ∠ ( ).
两直线平行,内错角相等.
两直线平行,内错角相等.
D
ACB
3. 如图,已知AB∥CD,AD∥BC.判断∠1与∠2是否相等,并说明理由.
∵AB∥CD,
∴∠2=∠BCE(两直线平行,内错角相等),
∵AD∥BC,
∴∠1=∠BCE(两直线平行,同位角相等),
∴∠1=∠2.
解
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结:
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
