苏科版七年级数学下册 7.4 认识三角形 课件(共19张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 7.4 认识三角形 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 189.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
7.4 认识三角形
由3条不在同一直线上的线段,首尾依次相接组成的图形叫做三角形.
三角形的概念:
认识三角形
A
B
C
a
记作:△ABC
三角形的顶点:点A、点B、点C
三角形的边: AB、 AC、 BC
三角形的内角:∠A 、 ∠B 、 ∠C
c
b
a
b
c
考考你!
(1)△ABD的顶点是
(3)以BD为边的三角形有
(2)以∠A为内角的三角形有
(4)△BCD的边是
点A、点D、点B
△ABD、△BDC
△ABD、 △ABC
BC、BD、CD
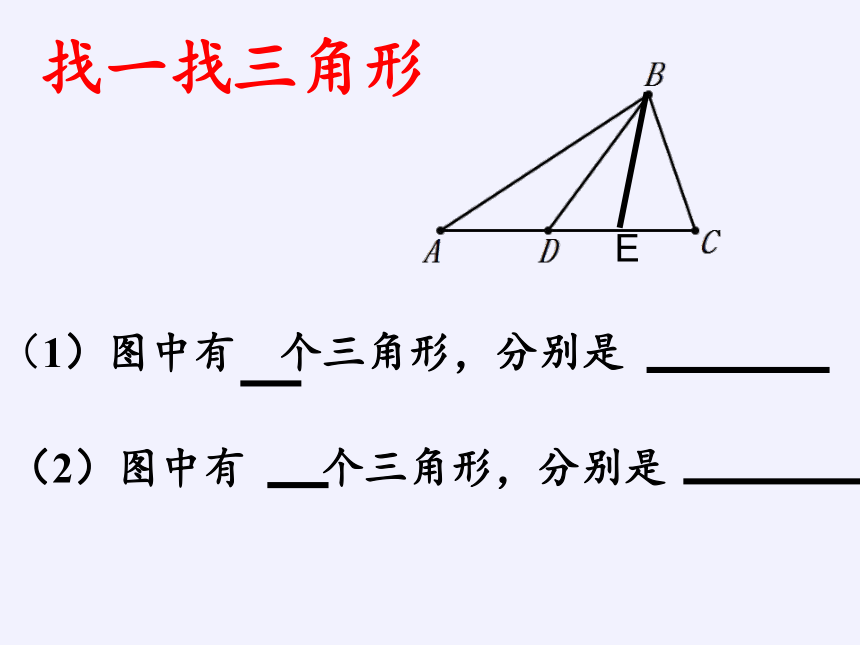
找一找三角形
(1)图中有 个三角形,分别是
(2)图中有 个三角形,分别是
E
(1) (2) (3)
————三个内角都是锐角的三角形
————有一个内角是直角的三角形
————有一个内角是钝角的三角形
锐角三角形
直角三角形
钝角三角形
三角形的分类
按
角
分
按
边
分
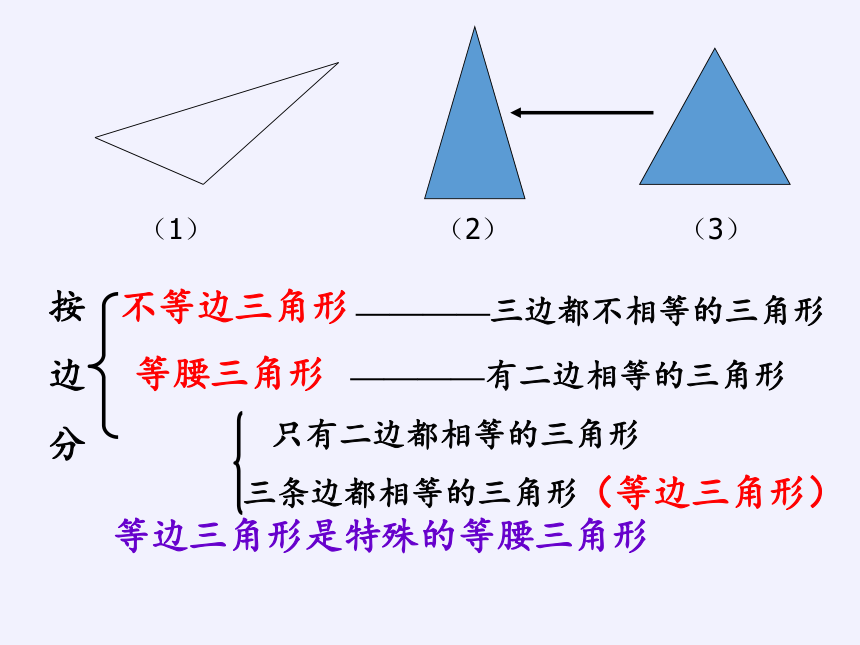
(1) (2) (3)
————三边都不相等的三角形
不等边三角形
等腰三角形
(等边三角形)
三条边都相等的三角形
等边三角形是特殊的等腰三角形
————有二边相等的三角形
只有二边都相等的三角形
探究活动二:
任意三条线段能否搭成三角形?
:
你能用数学知识说明为什么一个三角形任意两边之和大于第三边吗?
a + b > c
a + c > b
b + c > a
a
b
c
三角形的任意两边之和大于第三边。
三角形的三边关系:
a + b > c
a + c > b
b + c > a
符号语言:
人行横道
观察下图,联想实际,结合所学的数学知识解释此现象.
为什么经常有行人斜穿马路而不走人行横道?
.A
.B
议一议
C
BC+AC>AB
三条线段的长度分别为:
(1)3、8、10 (2)5、2、7
(3)5、5、11 (4)13、12、20
能组成三角形的有( )组。
A、1 B、2 C、3 D、4
技巧:
比较较小的两边之和与最长边的大小即可
B
考考你!
例:一个等腰三角形的两边分别为2.5和5, 求这个三角形的周长.
解:(1)若2.5为腰,则2.5+2.5=5
出现了两边之和等于第三边,所以
不能构 成三角形.
(2)若5为腰,则2.5+5=7.5>5,
任意两边之和大于第三边,所以能
构成三角形,所以三角形的周长
为:2.5+5+5=12.5
综上所述:三角形的周长为:
2.5+5+5=12.5
延伸拓展:
在河边修一个水泵站分别向甲、乙村送水,修在何处,可使水管AD+BD最短?
甲
乙
A
B
C
D
本节课你有什么收获?你还有什么不明白的吗?
课堂反馈:
1.如图,以BC为一边的三角形有: ;
以∠A为一个内角的三角形有: 。
2. 下列每组数表示3根小木棒的长度(单位:cm)。其中,能
用3根小木棒搭成一个三角形的是( )
A.3,4,7 B.3 ,4,6 C.5,7,12 D.2,3,6
3.(1)一个等腰三角形的一边是5cm,另一边是7cm,则这个三角
形的第三边是 cm.
(2)一个等腰三角形的一边是2cm,另一边是9cm ,则这个三角
形的第三边是 cm.
1877年,法国考古学家萨尔泽,在巴格达东南挖掘了美索不达米亚古城拉格什的遗址,他发现三座神庙之间的地下水道是按图甲连结,即A、B、C三座神庙中间的点P与A、B、C连结,经测量发现:PA+PB+PC阅读欣赏
费尔马点
阅读欣赏
1640年,大名鼎鼎的法国数学家费尔马向意大利物理学家托里拆利提出一个挑战性问题:在一个三角形所在的平面上找一点P,使它到三角形三个顶点的距离之和为最小.托里拆利和他的学生维微安尼经过一段时间的研究终于解决了这个问题,答案如图乙所示.这个特殊点P后来被称为费尔马点.
费尔马点
谢 谢
7.4 认识三角形
由3条不在同一直线上的线段,首尾依次相接组成的图形叫做三角形.
三角形的概念:
认识三角形
A
B
C
a
记作:△ABC
三角形的顶点:点A、点B、点C
三角形的边: AB、 AC、 BC
三角形的内角:∠A 、 ∠B 、 ∠C
c
b
a
b
c
考考你!
(1)△ABD的顶点是
(3)以BD为边的三角形有
(2)以∠A为内角的三角形有
(4)△BCD的边是
点A、点D、点B
△ABD、△BDC
△ABD、 △ABC
BC、BD、CD
找一找三角形
(1)图中有 个三角形,分别是
(2)图中有 个三角形,分别是
E
(1) (2) (3)
————三个内角都是锐角的三角形
————有一个内角是直角的三角形
————有一个内角是钝角的三角形
锐角三角形
直角三角形
钝角三角形
三角形的分类
按
角
分
按
边
分
(1) (2) (3)
————三边都不相等的三角形
不等边三角形
等腰三角形
(等边三角形)
三条边都相等的三角形
等边三角形是特殊的等腰三角形
————有二边相等的三角形
只有二边都相等的三角形
探究活动二:
任意三条线段能否搭成三角形?
:
你能用数学知识说明为什么一个三角形任意两边之和大于第三边吗?
a + b > c
a + c > b
b + c > a
a
b
c
三角形的任意两边之和大于第三边。
三角形的三边关系:
a + b > c
a + c > b
b + c > a
符号语言:
人行横道
观察下图,联想实际,结合所学的数学知识解释此现象.
为什么经常有行人斜穿马路而不走人行横道?
.A
.B
议一议
C
BC+AC>AB
三条线段的长度分别为:
(1)3、8、10 (2)5、2、7
(3)5、5、11 (4)13、12、20
能组成三角形的有( )组。
A、1 B、2 C、3 D、4
技巧:
比较较小的两边之和与最长边的大小即可
B
考考你!
例:一个等腰三角形的两边分别为2.5和5, 求这个三角形的周长.
解:(1)若2.5为腰,则2.5+2.5=5
出现了两边之和等于第三边,所以
不能构 成三角形.
(2)若5为腰,则2.5+5=7.5>5,
任意两边之和大于第三边,所以能
构成三角形,所以三角形的周长
为:2.5+5+5=12.5
综上所述:三角形的周长为:
2.5+5+5=12.5
延伸拓展:
在河边修一个水泵站分别向甲、乙村送水,修在何处,可使水管AD+BD最短?
甲
乙
A
B
C
D
本节课你有什么收获?你还有什么不明白的吗?
课堂反馈:
1.如图,以BC为一边的三角形有: ;
以∠A为一个内角的三角形有: 。
2. 下列每组数表示3根小木棒的长度(单位:cm)。其中,能
用3根小木棒搭成一个三角形的是( )
A.3,4,7 B.3 ,4,6 C.5,7,12 D.2,3,6
3.(1)一个等腰三角形的一边是5cm,另一边是7cm,则这个三角
形的第三边是 cm.
(2)一个等腰三角形的一边是2cm,另一边是9cm ,则这个三角
形的第三边是 cm.
1877年,法国考古学家萨尔泽,在巴格达东南挖掘了美索不达米亚古城拉格什的遗址,他发现三座神庙之间的地下水道是按图甲连结,即A、B、C三座神庙中间的点P与A、B、C连结,经测量发现:PA+PB+PC
费尔马点
阅读欣赏
1640年,大名鼎鼎的法国数学家费尔马向意大利物理学家托里拆利提出一个挑战性问题:在一个三角形所在的平面上找一点P,使它到三角形三个顶点的距离之和为最小.托里拆利和他的学生维微安尼经过一段时间的研究终于解决了这个问题,答案如图乙所示.这个特殊点P后来被称为费尔马点.
费尔马点
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
