苏科版七年级数学下册 9.4 乘法公式 课件(共23张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 9.4 乘法公式 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 149.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 15:37:40 | ||
图片预览






文档简介
(共23张PPT)
9.4 乘法公式
速算王的“绝招”
在一次智力抢答赛中,主持人提供了两道题,1. 21x19= ? 2. 105x95 ? 主持人话音刚落,就立刻有一个学生刷地站起来抢答说:第一题等于399,第二题等于9991.其速度之快,简直就是脱口而出。
同学们,你知道他是如何计算的吗?你想不想掌握他这种简便、快速的运算招数呢?
情景引入
1. 经历探索平方差公式的过程,发展符号感和推理能力;
2. 学会运用公式进行简单的乘法运算;
3. 培养语言表达和逻辑思维能力,在探索讨论中学会归纳总结。
学习目标
计算下列多项式的积:
(1) (x+1)(x-1) =
(2) (m+2)(m-2) =
(3)(2x+1)(2x-1) =
=x2 - 12
=m2 - 22
=(2x)2 - 12
x2-1
m2-4
4x2-1
规律探索
从上面的计算中,你有什么发现?
(a+b)(a-b) = a2-b2
(a+b)(a-b)
= a2-ab+ab-b2
-ab
+ab
= a2-b2
a2
b2
你还能用其它方法证明此结论的正确性吗?
你能用代数法验证这个规律吗?
规律验证1
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
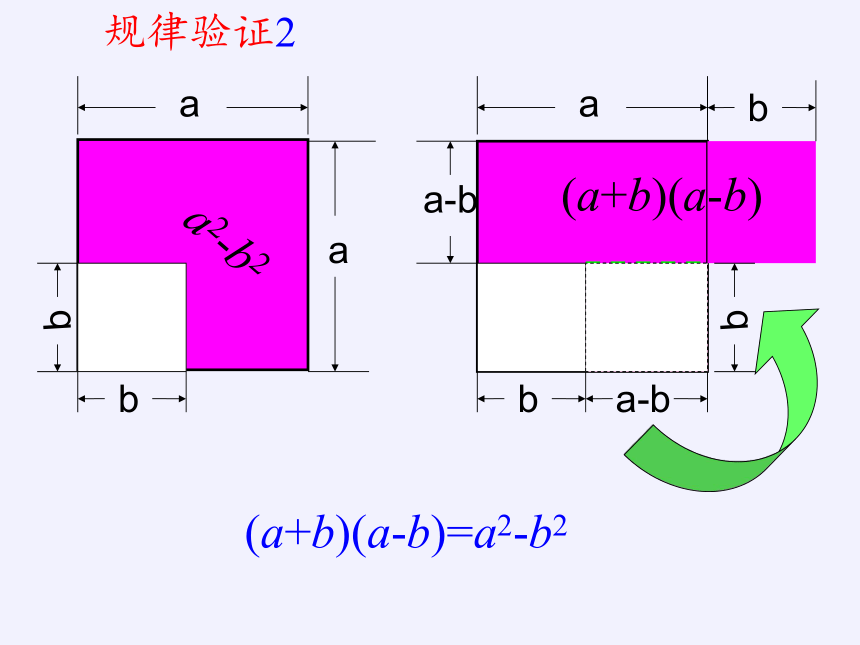
规律验证2
a
b
a
b
1
2
(a+b)(a-b)
1
2
(a+b)(a-b)
b
a-b
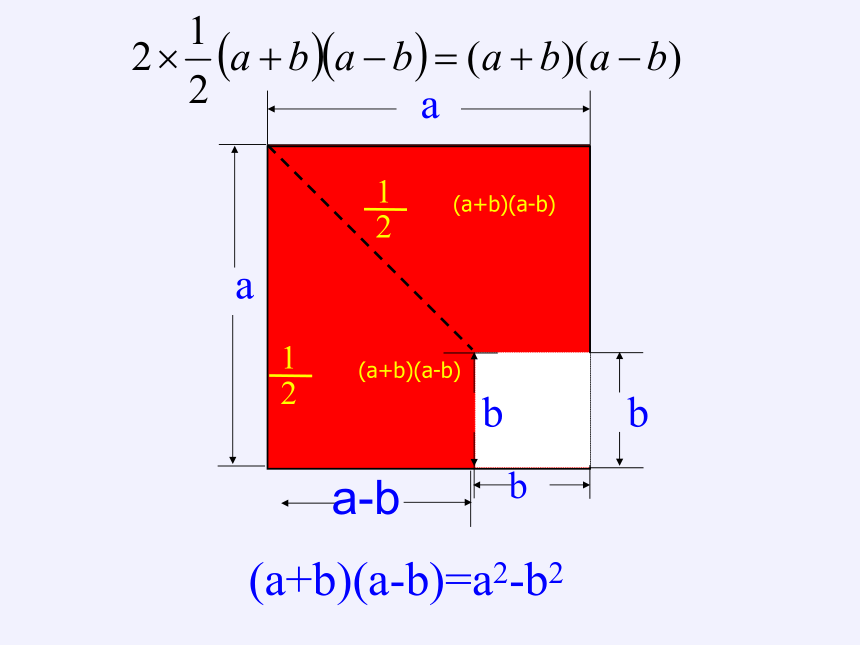
(a+b)(a-b)=a2-b2
b
a
a
b
(a+b)(a-b)
=
a2-b2
(a+b)(a-b)=a2-b2
规律验证2
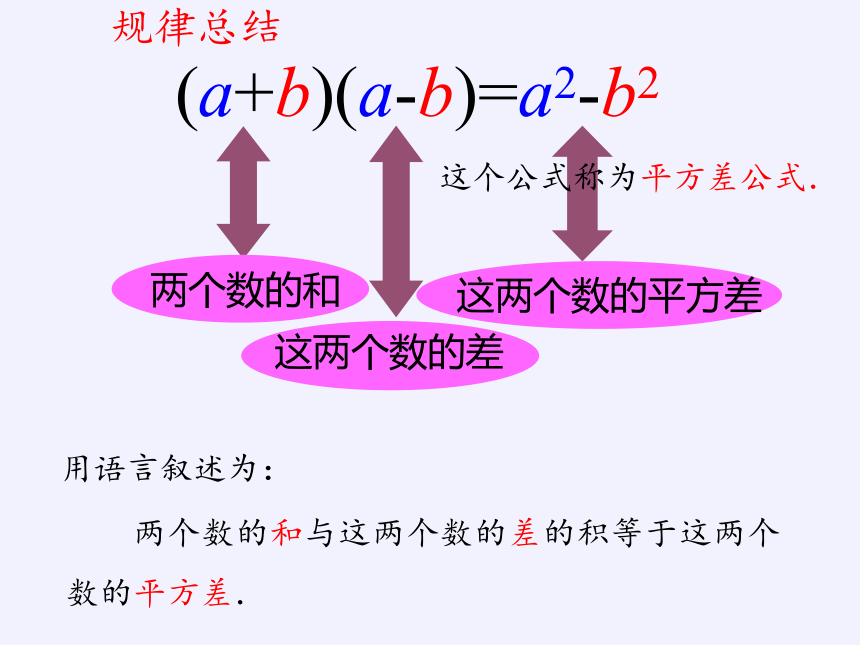
(a+b)(a-b)=a2-b2
两个数的和
这两个数的差
这两个数的平方差
这个公式称为平方差公式.
两个数的和与这两个数的差的积等于这两个数的平方差.
用语言叙述为:
规律总结
(a+b)(a-b)=a2-b2
两个二项式相乘
相同项
相反数的项
结构特征
(a+b)(a-b)=a2-b2
(相同项)2-(相反项)2
平方差
结构特征
(a+b)(a-b)=a2-b2
结构特征
(1)左边是两个二项式的乘积,其中一项完全相同,另一项互为相反数;
(2)右边是这两项的平方差,即相同项的平方( a2 )减去相反项的平方( b2 );
(3) 公式中的a、b可以表示数,也可以表示单项式或多项式.
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
找一找,填一填
判断下列各式可以利用平方差公式吗?如果能,公式中的a、b分别代表什么?如果不能,说出理由。
①
②
③
④
(a+b)(a-b)=a2-b2
⑤
(x2+1)( x2-1 )
1.选择:下列各式中,能用平方差公式的是( ) A. (x-3)(-x+3) B(x+2y)(2x-y)
C. (y-1)(-y-1) D.(y+1)(-y-1)
2.下列多项式乘法中,能用平方差公的是
(1) (x+1)(1+x) (2) (a+b)(b-a)
(3) (-a+b)(a-b) (4) (x2-y)(x+y2)
(5) (-a-b)(a-b) (6) (c2-d2)(d2+c2)
c
(2)
(5)
(6)
例1 用平方差公式计算:
(1)
(2)
(3)
基础练习
例2 用简便方法计算:
(1)103×97;
(2)
×
基础练习
你知道“速算王的‘绝招’”了吗?
1.小组内相互列举可以运用平方差公式计算的多项式乘多项式的算式;
2.利用平方差公式进行计算时需要注意哪些问题.
例3 用平方差公式计算:
(1)
(2)
能力提升
(x2+y)( x2-y )
(5x2+3y)(-3y+5x2 )
拓展提升
如何计算 ?
将 看成一个整体a
通过本节课的学习,你有什么收获?在用平方差公式时应注意什么问题?
课堂小结
作业:
完成导学案的检测题
谢 谢
9.4 乘法公式
速算王的“绝招”
在一次智力抢答赛中,主持人提供了两道题,1. 21x19= ? 2. 105x95 ? 主持人话音刚落,就立刻有一个学生刷地站起来抢答说:第一题等于399,第二题等于9991.其速度之快,简直就是脱口而出。
同学们,你知道他是如何计算的吗?你想不想掌握他这种简便、快速的运算招数呢?
情景引入
1. 经历探索平方差公式的过程,发展符号感和推理能力;
2. 学会运用公式进行简单的乘法运算;
3. 培养语言表达和逻辑思维能力,在探索讨论中学会归纳总结。
学习目标
计算下列多项式的积:
(1) (x+1)(x-1) =
(2) (m+2)(m-2) =
(3)(2x+1)(2x-1) =
=x2 - 12
=m2 - 22
=(2x)2 - 12
x2-1
m2-4
4x2-1
规律探索
从上面的计算中,你有什么发现?
(a+b)(a-b) = a2-b2
(a+b)(a-b)
= a2-ab+ab-b2
-ab
+ab
= a2-b2
a2
b2
你还能用其它方法证明此结论的正确性吗?
你能用代数法验证这个规律吗?
规律验证1
a
a
b
b
a2-b2
a
b
b
b
(a+b)(a-b)
(a+b)(a-b)=a2-b2
a-b
a-b
规律验证2
a
b
a
b
1
2
(a+b)(a-b)
1
2
(a+b)(a-b)
b
a-b
(a+b)(a-b)=a2-b2
b
a
a
b
(a+b)(a-b)
=
a2-b2
(a+b)(a-b)=a2-b2
规律验证2
(a+b)(a-b)=a2-b2
两个数的和
这两个数的差
这两个数的平方差
这个公式称为平方差公式.
两个数的和与这两个数的差的积等于这两个数的平方差.
用语言叙述为:
规律总结
(a+b)(a-b)=a2-b2
两个二项式相乘
相同项
相反数的项
结构特征
(a+b)(a-b)=a2-b2
(相同项)2-(相反项)2
平方差
结构特征
(a+b)(a-b)=a2-b2
结构特征
(1)左边是两个二项式的乘积,其中一项完全相同,另一项互为相反数;
(2)右边是这两项的平方差,即相同项的平方( a2 )减去相反项的平方( b2 );
(3) 公式中的a、b可以表示数,也可以表示单项式或多项式.
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
找一找,填一填
判断下列各式可以利用平方差公式吗?如果能,公式中的a、b分别代表什么?如果不能,说出理由。
①
②
③
④
(a+b)(a-b)=a2-b2
⑤
(x2+1)( x2-1 )
1.选择:下列各式中,能用平方差公式的是( ) A. (x-3)(-x+3) B(x+2y)(2x-y)
C. (y-1)(-y-1) D.(y+1)(-y-1)
2.下列多项式乘法中,能用平方差公的是
(1) (x+1)(1+x) (2) (a+b)(b-a)
(3) (-a+b)(a-b) (4) (x2-y)(x+y2)
(5) (-a-b)(a-b) (6) (c2-d2)(d2+c2)
c
(2)
(5)
(6)
例1 用平方差公式计算:
(1)
(2)
(3)
基础练习
例2 用简便方法计算:
(1)103×97;
(2)
×
基础练习
你知道“速算王的‘绝招’”了吗?
1.小组内相互列举可以运用平方差公式计算的多项式乘多项式的算式;
2.利用平方差公式进行计算时需要注意哪些问题.
例3 用平方差公式计算:
(1)
(2)
能力提升
(x2+y)( x2-y )
(5x2+3y)(-3y+5x2 )
拓展提升
如何计算 ?
将 看成一个整体a
通过本节课的学习,你有什么收获?在用平方差公式时应注意什么问题?
课堂小结
作业:
完成导学案的检测题
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
