8.2.2一元线性回归模型参数的最小二乘估计教学设计-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 8.2.2一元线性回归模型参数的最小二乘估计教学设计-2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册 |  | |
| 格式 | docx | ||
| 文件大小 | 765.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 16:42:51 | ||
图片预览

文档简介
8.2.2一元线性回归模型参数的最小二乘估计
(人教A版普通高中教科书数学选择性必修第三册第八章)
一、教学目标
1.理解最小二乘法
2.理解并掌握经验回归直线
3.理解残差分析
二、教学重难点
1.利用最小二乘法推到经验回归方程
2.利用经验回归方程解决实际问题
三、教学过程
为了研究两个变量之间的相关关系,我们建立了一元线性回归模型,表达式 刻画的是变量Y与变量x之间的线性相关关系,其中参数a和b未知,需要根据成对样本数据进行估计.
由模型的建立过程可知,参数a和b刻画了变量Y与变量x的线性关系,因此通过成对样本数据估计这两个参数,相当于寻找一条适当的直线,使表示成对样本数据的这些散点在整体上与这条直线最接近.
问题1:从成对样本数据出发,如何用数学的方法刻画“从整体上看,各散点与直线最接近”?
【设计意图】明确问题,指明思考的方向,引发学生思考.
思路1:先画出一条直线,测量出各点到直线的距离,然后移动直线,到达一个使距离的和最小的位置,测量出此时的斜率和截距,就得到一条直线.
思路2:可以在散点图中选两点画一条直线,使得直线两侧点的个数基本相同,把这条直线作为所求直线.
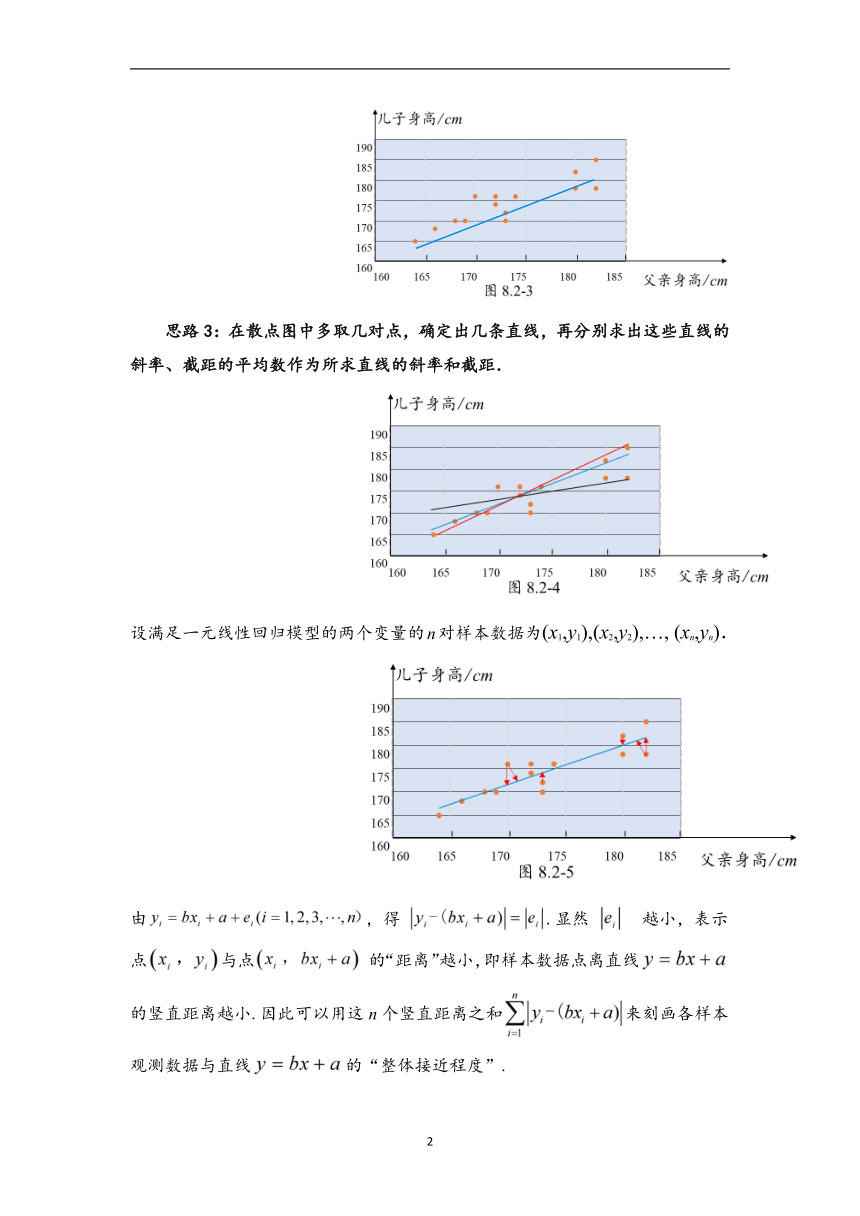
思路3:在散点图中多取几对点,确定出几条直线,再分别求出这些直线的斜率、截距的平均数作为所求直线的斜率和截距.
设满足一元线性回归模型的两个变量的n对样本数据为(x1,y1),(x2,y2),…, (xn,yn).
由,得 .显然 越小,表示点与点的“距离”越小,即样本数据点离直线的竖直距离越小.因此可以用这n个竖直距离之和来刻画各样本观测数据与直线的“整体接近程度”.
问题2:如何求a,b的值,使 最小?
【设计意图】将距离最值问题抽象为函数求二元函数最值问题.
我们将称为Y 关于x 的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线,这种求经验回归方程的方法叫最小二乘法,求得的 , 叫做b,a的最小二乘估计.
问题3:如何理解经验回归直线?
1)当x=176时,,如果一位父亲身高为176cm,他儿子长大后身高一定能长到177cm吗?为什么?
2)根据模型,父亲身高为多少时,儿子的平均身高与父亲的一样?
3)斜率0.839有什么含义?
对于响应变量Y,通过观测得到的数据为观测值,通过经验回归方程得到的称为预测值,观测值减去预测值称为残差.
问题4:如何判断模型刻画数据的效果?
问题5:观察以下四幅残差图,你认为哪一个残差满足一元线性回归模型中对随机误差的假定?
四、课后作业:
教科书第113页练习第2、3题.
5
(人教A版普通高中教科书数学选择性必修第三册第八章)
一、教学目标
1.理解最小二乘法
2.理解并掌握经验回归直线
3.理解残差分析
二、教学重难点
1.利用最小二乘法推到经验回归方程
2.利用经验回归方程解决实际问题
三、教学过程
为了研究两个变量之间的相关关系,我们建立了一元线性回归模型,表达式 刻画的是变量Y与变量x之间的线性相关关系,其中参数a和b未知,需要根据成对样本数据进行估计.
由模型的建立过程可知,参数a和b刻画了变量Y与变量x的线性关系,因此通过成对样本数据估计这两个参数,相当于寻找一条适当的直线,使表示成对样本数据的这些散点在整体上与这条直线最接近.
问题1:从成对样本数据出发,如何用数学的方法刻画“从整体上看,各散点与直线最接近”?
【设计意图】明确问题,指明思考的方向,引发学生思考.
思路1:先画出一条直线,测量出各点到直线的距离,然后移动直线,到达一个使距离的和最小的位置,测量出此时的斜率和截距,就得到一条直线.
思路2:可以在散点图中选两点画一条直线,使得直线两侧点的个数基本相同,把这条直线作为所求直线.
思路3:在散点图中多取几对点,确定出几条直线,再分别求出这些直线的斜率、截距的平均数作为所求直线的斜率和截距.
设满足一元线性回归模型的两个变量的n对样本数据为(x1,y1),(x2,y2),…, (xn,yn).
由,得 .显然 越小,表示点与点的“距离”越小,即样本数据点离直线的竖直距离越小.因此可以用这n个竖直距离之和来刻画各样本观测数据与直线的“整体接近程度”.
问题2:如何求a,b的值,使 最小?
【设计意图】将距离最值问题抽象为函数求二元函数最值问题.
我们将称为Y 关于x 的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线,这种求经验回归方程的方法叫最小二乘法,求得的 , 叫做b,a的最小二乘估计.
问题3:如何理解经验回归直线?
1)当x=176时,,如果一位父亲身高为176cm,他儿子长大后身高一定能长到177cm吗?为什么?
2)根据模型,父亲身高为多少时,儿子的平均身高与父亲的一样?
3)斜率0.839有什么含义?
对于响应变量Y,通过观测得到的数据为观测值,通过经验回归方程得到的称为预测值,观测值减去预测值称为残差.
问题4:如何判断模型刻画数据的效果?
问题5:观察以下四幅残差图,你认为哪一个残差满足一元线性回归模型中对随机误差的假定?
四、课后作业:
教科书第113页练习第2、3题.
5
