苏科版七年级数学下册 第7章 平面图形的认识(二) 课件(共10张PPT)
文档属性
| 名称 | 苏科版七年级数学下册 第7章 平面图形的认识(二) 课件(共10张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 103.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 10:32:13 | ||
图片预览




文档简介
(共10张PPT)
小结与思考
1.定义
2.命题
整体感知
3.证明
4.互逆命题
1.下列语句中,属于定义的是( )
A.两点确定一条直线
B.两点之间线段最短
C.平行线的同位角相等
D.直线外一点到直线的垂线段的长度,
叫做点到直线的距离
基础提炼
2. 判断下面句子哪些是命题?如果是命题指出它的
条件和结论,并说明是真命题还是假命题?
(1)画一个角等于已知角.
(3)同位角相等吗?
(2)内错角相等.
(4)两直线平行,同位角相等.
基础提炼
(5)对顶角相等.
说出(4)和(5)的逆命题,并说明逆命题是真命题还是假命题?
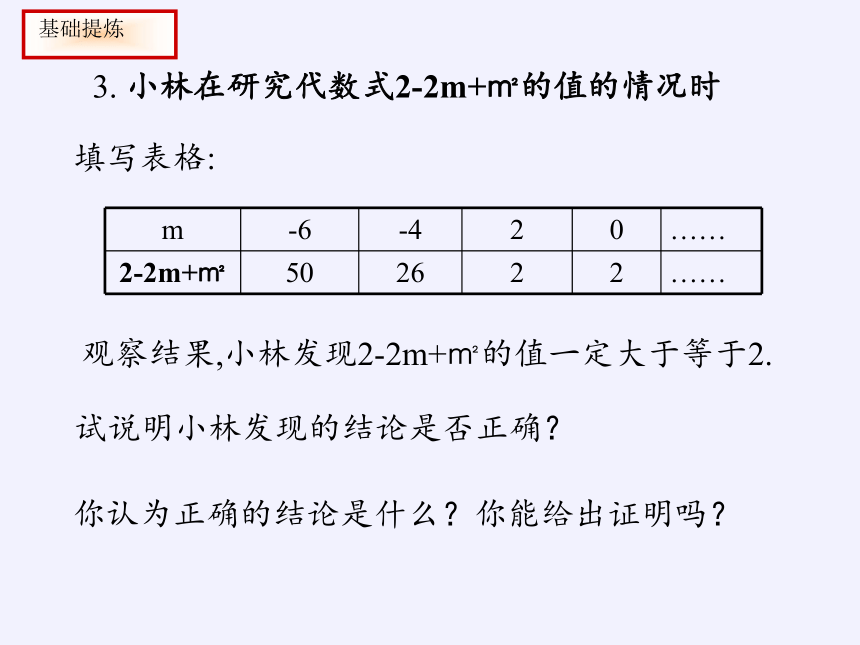
3. 小林在研究代数式2-2m+㎡的值的情况时
填写表格:
m -6 -4 2 0 ……
2-2m+㎡ 50 26 2 2 ……
观察结果,小林发现2-2m+㎡的值一定大于等于2.
试说明小林发现的结论是否正确?
基础提炼
你认为正确的结论是什么?你能给出证明吗?
例1.证明:平面内垂直于同一条直线的两条直线
互相平行.
典型分析
例2.已知:如图,AC、BD 相交于点O .
A
O
C
D
B
求证:∠A+∠B= ∠C+∠D.
A
O
C
D
B
变化发展
(课本P156页)
已知:如图,△ABC中,∠A=∠ABC,直线 EF
分别交AB、AC和CB的延长线于点D、E、F.
(1)求证:∠F+∠FEC= 2∠A
变化发展
(2)过点B作BG∥AC交EF于G.
求证:AB平分∠GBC
命题:判断、句子
命题的结构:条件与结论 命题的真假
总结提升
证明:
证明的必要性 代数证明 几何证明
假命题的证明方法:举反例
互逆命题
命题证明步骤:画图、写已知求证、证明.
命题证明的一般思考方法:综合、分析
定义: 描述、规定
谢 谢
小结与思考
1.定义
2.命题
整体感知
3.证明
4.互逆命题
1.下列语句中,属于定义的是( )
A.两点确定一条直线
B.两点之间线段最短
C.平行线的同位角相等
D.直线外一点到直线的垂线段的长度,
叫做点到直线的距离
基础提炼
2. 判断下面句子哪些是命题?如果是命题指出它的
条件和结论,并说明是真命题还是假命题?
(1)画一个角等于已知角.
(3)同位角相等吗?
(2)内错角相等.
(4)两直线平行,同位角相等.
基础提炼
(5)对顶角相等.
说出(4)和(5)的逆命题,并说明逆命题是真命题还是假命题?
3. 小林在研究代数式2-2m+㎡的值的情况时
填写表格:
m -6 -4 2 0 ……
2-2m+㎡ 50 26 2 2 ……
观察结果,小林发现2-2m+㎡的值一定大于等于2.
试说明小林发现的结论是否正确?
基础提炼
你认为正确的结论是什么?你能给出证明吗?
例1.证明:平面内垂直于同一条直线的两条直线
互相平行.
典型分析
例2.已知:如图,AC、BD 相交于点O .
A
O
C
D
B
求证:∠A+∠B= ∠C+∠D.
A
O
C
D
B
变化发展
(课本P156页)
已知:如图,△ABC中,∠A=∠ABC,直线 EF
分别交AB、AC和CB的延长线于点D、E、F.
(1)求证:∠F+∠FEC= 2∠A
变化发展
(2)过点B作BG∥AC交EF于G.
求证:AB平分∠GBC
命题:判断、句子
命题的结构:条件与结论 命题的真假
总结提升
证明:
证明的必要性 代数证明 几何证明
假命题的证明方法:举反例
互逆命题
命题证明步骤:画图、写已知求证、证明.
命题证明的一般思考方法:综合、分析
定义: 描述、规定
谢 谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
