第二十章数据的分析练习题2020-2021学年吉林省部分地区八年级下学期人教版数学期末试题选编(Word版含解析)
文档属性
| 名称 | 第二十章数据的分析练习题2020-2021学年吉林省部分地区八年级下学期人教版数学期末试题选编(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 295.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 19:47:28 | ||
图片预览




文档简介
第二十章:数据的分析练习题
一、单选题
1.(2021·吉林经济技术开发区·八年级期末)若四个数据10,15,x,20的平均数是15,那么x的值为( )
A.10 B.20 C.15 D.25
2.(2021·吉林宽城·八年级期末)某校评选先进班集体,从“学习”、“卫生”、“纪律”、“活动参与”四个方面考核打分,各项满分均为,所占比例如下表:
项目 学习 卫生 纪律 活动参与
所占比例
八年级班这四项得分依次为,,,,则该班四项综合得分(满分)为( )
A. B. C. D.
3.(2021·吉林铁西·八年级期末)在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
4.(2021·吉林伊通·八年级期末)某校七年级有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的( )
A.中位数 B.众数 C.平均数 D.极差
5.(2021·吉林德惠·八年级期末)为筹备班级联欢会,班长对全班同学爱吃哪几种水果做了民意调查,然后决定买什么水果,最值得关注的应该是统计调查数据的( )
A.中位数 B.平均数 C.众数 D.方差
6.(2021·吉林靖宇·八年级期末)数据2,3,5,5,4的众数是( ).
A.2 B.3 C.4 D.5
7.(2021·吉林梅河口·八年级期末)每年的6月5日为世界环境保护日,为提高学生环境保护意识,某校对100名学生进行“保护环境知多少”测试,抽取部分统计如下表:
成绩(分) 60 70 80 90 100
人数(人) 7 20 23 42 8
本次测验成绩的众数为( )
A.80分 B.85分 C.90分 D.100分
8.(2021·吉林双辽·八年级期末)一组数据8,7,6,7,6,5,4,5,8,6的众数是( )
A.8 B.7 C.6 D.5
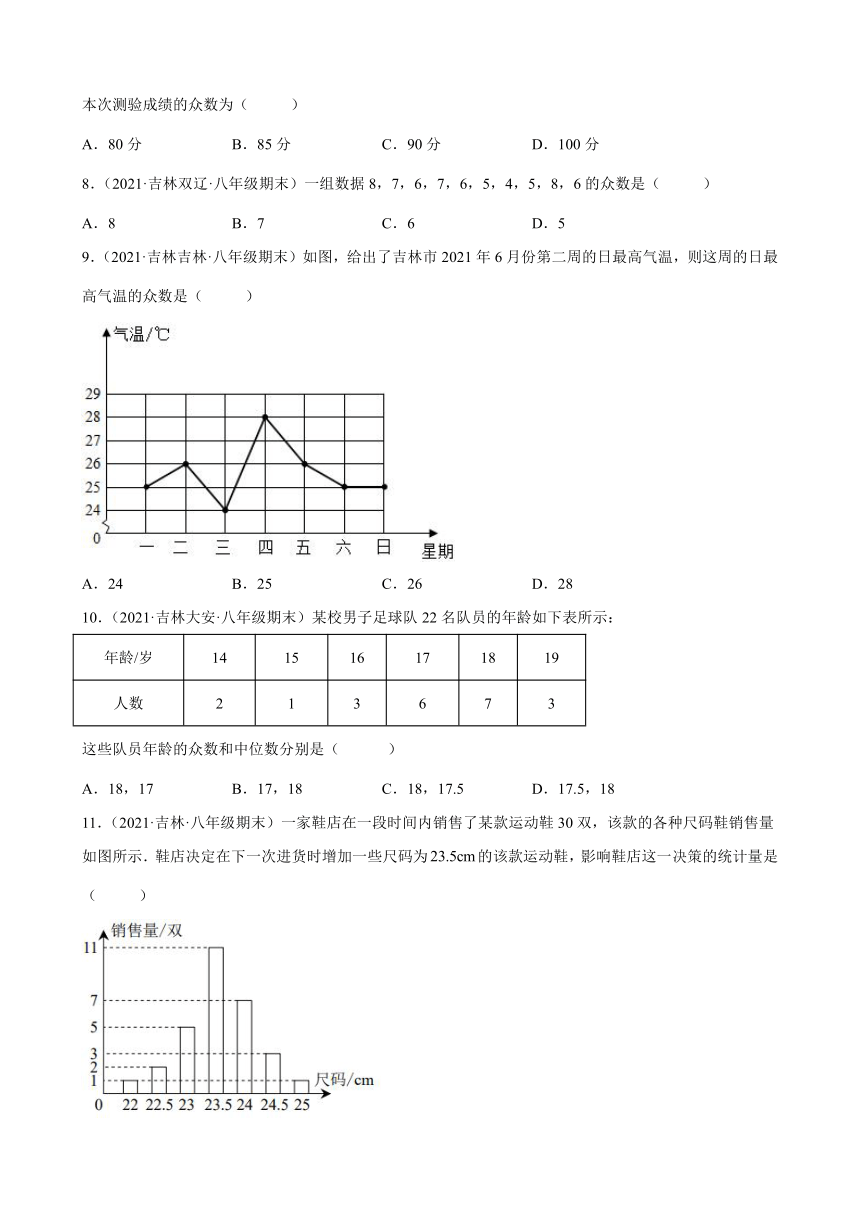
9.(2021·吉林吉林·八年级期末)如图,给出了吉林市2021年6月份第二周的日最高气温,则这周的日最高气温的众数是( )
A.24 B.25 C.26 D.28
10.(2021·吉林大安·八年级期末)某校男子足球队22名队员的年龄如下表所示:
年龄/岁 14 15 16 17 18 19
人数 2 1 3 6 7 3
这些队员年龄的众数和中位数分别是( )
A.18,17 B.17,18 C.18,17.5 D.17.5,18
11.(2021·吉林·八年级期末)一家鞋店在一段时间内销售了某款运动鞋30双,该款的各种尺码鞋销售量如图所示.鞋店决定在下一次进货时增加一些尺码为的该款运动鞋,影响鞋店这一决策的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
12.(2021·吉林朝阳·八年级期末)为参加学校举办的“诗意校园 致远方”朗诵艺术大赛,八年级“屈原读书社”组织了五次选拔赛,这五次选拔赛中,小明五次成绩的平均数是90,方差是2;小强五次成绩的平均数也是90,方差是14.8.下列说法正确的是( )
A.小明的成绩比小强稳定
B.小明、小强两人成绩一样稳定
C.小强的成绩比小明稳定
D.无法确定小明、小强的成绩谁更稳定
13.(2021·吉林桦甸·八年级期末)某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )
A.平均分不变,方差变大 B.平均分不变,方差变小
C.平均分和方差都不变 D.平均分和方差都改变
14.(2021·吉林双阳·八年级期末)数学老师对小明的5次单元测验成绩进行统计分析,要判断小明的数学成绩是否稳定,老师需要知道小明这5次数学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
15.(2021·吉林德惠·八年级期末)某玩具厂质检员对A,B,C,D,E这5个玩具进行称重,实际重量分别为:90,87,92,92,91(单位:克).在统计时,不小心将B玩具的重量写成了90克,则计算结果不受影响的是( )
A.平均数 B.众数 C.中位数 D.方差
16.(2021·吉林·舒兰市教师进修学校八年级期末)甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均数都是8.9环,方差分别是,,,,则射箭成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
17.(2021·吉林汽车经济技术开发区·八年级期末)甲、乙、丙、丁四名学生近4次数学成绩的平均数都是108分,方差如下表,则这四名学生成绩最稳定的是( )
学生 甲 乙 丙 丁
方差(s2) 86 51.5 63.5 19.5
A.甲 B.乙 C.丙 D.丁
二、填空题
18.(2021·吉林靖宇·八年级期末)某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是_____分.
19.(2021·吉林桦甸·八年级期末)某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试得分分别为92分、85分、90分,综合成绩笔试占40%,试讲占40%,面试占20%,则该名教师的综合成绩为_______分.
20.(2021·吉林农安·八年级期末)一组数3,4,7,4,3,4,5,6,5的众数是_____.
21.(2021·吉林大安·八年级期末)甲、乙两名射击手的50次测试的平均成绩都是8环,方差分别是,则成绩比较稳定的是___(填“甲”或“乙”)
22.(2021·吉林·八年级期末)如果一组数据4,x,2,3,6的平均数是4,那么x是_____.
23.(2021·吉林双辽·八年级期末)在学校团体操比赛中,甲、乙两个班的同学身高的平均数相同,方差分别是 ,,那么身高整齐的是_____班.
24.(2021·吉林南关·八年级期末)某公司决定招聘广告策划人员一人,某应聘者三项素质测试的成绩(单位:分)如下:
测试项目 创新能力 综合知识 语言表达
测试成绩 90 80 75
如果将创新能力、综合能力和语言表达三项素质测试成绩按的比确定应聘者的最终成绩,则应聘者的最终成绩为______分.
25.(2021·吉林汽车经济技术开发区·八年级期末)小明在参加岗位应聘中,专业知识、工作经验、仪表形象三项的得分分别为:18分、15分、16分.若这三项的重要性之比为5:3:2,则他最终的得分是 _______分.
26.(2021·吉林铁西·八年级期末)已知一组数据:1,3,a,8,10的平均数是5,则a=___.
27.(2021·吉林吉林·八年级期末)某足球队23名队员年龄情况如表所示,这23名队员年龄的中位数是______.
年龄(岁) 21 22 23 24 25 26
人数 2 4 5 6 4 2
28.(2021·吉林经济技术开发区·八年级期末)已知一组数据-1,4,x,6,15的众数为6,那么这组数据的中位数是____.
三、解答题
29.(2021·吉林大安·八年级期末)小手拉大手,共创文明城.某校为了了解家长对南宁市创建全国文明城市相关知识的知晓情况,通过发放问卷进行测评,从中随机抽取份答卷,并统计成绩(成绩得分用表示,单位:分),收集数据如下:
整理数据:
分析数据:
平均分 中位数 众数
根据以上信息,解答下列问题:
(1)直接写出上述表格中的值;
(2)该校有名家长参加了此次问卷测评活动,请估计成绩不低于分的人数是多少?
(3)请从中位数和众数中选择一个量, 结合本题解释它的意义.
30.(2021·吉林农安·八年级期末)某同学参加了学校举行的“五好小公民 红旗飘飘”演讲比赛,7名评委给该同学的打分(单位:分)情况如下表:
评委 评委1 评委2 评委3 评委4 评委5 评委6 评委7
打分 6 8 7 8 5 7 8
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数
31.(2021·吉林双辽·八年级期末)在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成如图所示的统计图.
(1)本次调查的人数是 ;
(2)这组数据的众数为 元,中位数为 元;
(3)求这组数据的平均数.
32.(2021·吉林德惠·八年级期末)为了加强安全教育,某校对学生进行“防溺水知识应知应答”测评.该校随机选取了八年级300名学生中的20名学生在10月份测评的成绩,数据如下:
收集数据:
97 91 89 95 90 99 90 97 91 98
90 90 91 88 98 97 95 90 96 88
整理、描述数据:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 5 2 1 3 1
数据分析:样本数据的平均数、众数和中位数如表:
平均数 中位数 众数
93
(1) , , , ;
(2)该校决定授予在10月份测评成绩优秀(96分及以上)的八年级的学生“防溺水小卫士”荣誉称号,请估计评选该荣誉称号的人数.
(3)若被选取的20名学生在11月份测评的成绩的平均数、众数和中位数如表:
平均数 中位数 众数
95 93 94
结合相关数据,从一个方面评价10月份到11月份开展的“防溺水知识应知应答”测评活动的效果.
33.(2021·吉林前郭尔罗斯·八年级期末)射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 第二次 第三次 第四次 第五次 第六次 平均成绩 中位数
甲 10 8 9 8 10 9 9 ①
乙 10 7 10 10 9 8 ② 9.5
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为,你认为推荐谁参加比赛更合适,请说明理由.
34.(2021·吉林铁西·八年级期末)我校小李同学对北大附中初中三个年级的学生年龄构成很感兴趣,整理数据并绘制如图所示不完整的统计图.依据信息解答下列问题.
(1)求样本容量;
(2)直接写出样本数据的众数、中位数;
(3)已知北大附中实验学校一共有1920名学生,请估计全校年龄在14岁及以上的学生大约有多少人.
35.(2021·吉林宽城·八年级期末)某校拟派一名跳高运动员参加校际比赛,对甲、乙两名同学进行了8次跳高选拔比赛,他们的原始成绩(单位:cm)如下表:
次数 成绩 学生 第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次
甲 169 165 168 169 172 173 169 167
乙 161 174 172 162 163 172 172 176
两名同学的8次跳高成绩数据分析如下表:
名称 成绩 学生 平均数 (单位:cm) 中位数 (单位:cm) 众数 (单位:cm) 方差 (单位:cm2)
甲 a b c 5.75
乙 169 172 172 31.25
根据图表信息回答下列问题:
(1)求a、b、c的值.
(2)这两名同学中, 的成绩更为稳定(填“甲”或“乙”).
(3)若预测跳高165cm就可能获得冠军,该校为了获取跳高比赛冠军,你认为应该选择哪位同学参赛,并说明理由
36.(2021·吉林桦甸·八年级期末)在新冠状病毒防控期间,各地纷纷展开了停课不停学活动,学校为了了解学生自主阅读情况,抽样调查了部分学生每周用于自主阅读的时间,过程如下:
收集数据:
从全校随机抽取20名学生,每周用于自主阅读时间的调查,数据如下:(单位:)
30 60 81 50 44 110 130 146 80 100
60 80 120 140 75 81 10 30 81 92
整理数据:按下表分段整理样本数据:
自主阅读时间
等级 A
人数 3 8 4
分析数据:样本的平均数、中位数、众数如下表所示:
平均数 中位数 众数
80
请回答下列问题:
(1)表格中的数据_______,________,_______;
(2)用样本中的统计量估计该校学生每周用于课外阅读时间的等级为______;
(3)假设平均阅读一本课外书的时间为320分钟,请你用样本平均数估计该校学生每人一年(按52周计算)平均阅读________本课外书.
37.(2021·吉林汽车经济技术开发区·八年级期末)第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,某校对七、八年级全体学生进行了相关知识测试,然后从七、八年级各随机抽取了20名学生的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
Ⅰ.七年级20名学生成绩的频数分布表如下:
七年级学生样本成绩频数分布表
成绩m(分) 频数(人数)
50≤m<60 1
60≤m<70 2
70≤m<80 3
80≤m<90 8
90≤m≤100 6
合计 20
Ⅱ.七年级20名学生成绩在80≤m<90这一组的具体成绩是:
87 88 88 88 89 89 89 89
Ⅲ.七、八年级学生样本成绩的平均数、中位数、众数如下表所示:
平均数 中位数 众数
七年级 84 n 89
八年级 84.2 85 85
根据以上提供的信息,解答下列问题:
(1)表中n的值为 .
(2)在学生样本成绩中,某学生的成绩是87分,在他所属年级抽取的学生中排在前10名,根据表中数据判断该学生所在年级,并说明理由.
(3)七年级共有学生180名,若将不低于80分的成绩定为优秀,请估计七年级成绩优秀的学生人数.
38.(2021·吉林伊通·八年级期末)2013年我省松原地震后,某中学开展了“我为灾区献爱心”捐款活动,八年级一班的团支部对全班50人捐款数额进行了统计,并绘制了下面统计图.
(1)把统计图补充完整;
(2)直接写出这组数据的众数和中位数;
(3)该校共有学生1600人,请你根据八年级一班的捐款情况,估计该中学的捐款总数.
39.(2021·吉林南关·八年级期末)每年的4月15日是我国全民国家安全教育日,某中学在全校七、八年级学生中开展了“国家安全法”知识竞赛.为了解七、八年级学生对“国家安全法”知识的掌握情况,现从七、八年级各随机抽取20名学生的竞赛成绩(百分制),分数如下:
七年级:82,58,73,80,75,74,85,64,75,95,75,79,82,68,75,80,92,85,84,79
八年级:92,72,90,81,72,81,93,82,78,83,80,81,71,81,72,77,82,80,70,41
对以上数据进行整理分析,得到下列表一和表二:
表一
七年级 0 2 7 2
八年级 1 0 0 7 9 3
表二
平均数 众数 中位数
七年级 78
八年级 78 80.5
根据以上信息,解答下列问题:
(1)的值为 ,的值为 ,的值为 ,的值为 .
(2)若该校七、八年级各有600人,估计该校七、八年级在本次竞赛成绩在90分以上的共有多少人.
(3)你认为哪个年级学生对“国家安全法”知识掌握的总体水平较好?请说明理由.
40.(2021·吉林吉林·八年级期末)某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表:(单位:分)
项目 选手 阅读能力 思维能力 表达能力
甲 94 87 74
乙 96 82 80
(1)甲、乙两人“三项测试”的平均成绩分别为 分、 分;
(2)根据实际需要,公司将阅读能力、思维能力和表达能力三项测试成绩按3:5:2的比确定每位应聘者的成绩,请你计算甲、乙两人的平均成绩,从他们的成绩看,应该录取谁?
试卷第1页,共3页
参考答案:
1.C
【分析】
运用平均数的计算公式即可求得的值.
【详解】
解:根据题意知,
解得:,
故选:C.
【点睛】
本题考查了算术平均数的求法.熟记公式是解决本题的关键.
2.B
【分析】
根据加权平均数的定义计算可得.
【详解】
解:80×40%+90×25%+84×25%+70×10%=82.5(分)
故选:B
【点睛】
本题主要考查平均数,解题的关键是掌握算术平均数和加权平均数的定义.
3.B
【分析】
由于比赛取前5名参加决赛,共有11名选手参加,根据中位数的意义分析即可.
【详解】
11个不同的成绩按从小到大排序后,中位数及中位数之后的共有5个数,
故只要知道自己的成绩和中位数就可以知道是否进入决赛了.
故选B.
【点睛】
本题考查了中位数意义.解题的关键是正确的求出这组数据的中位数.
4.A
【详解】
共有13名学生参加竞赛,取前6名,所以小梅需要知道自己的成绩是否进入前六.我们把所有同学的成绩按大小顺序排列,第7名学生的成绩是这组数据的中位数,所以小梅知道这组数据的中位数,才能知道自己是否进入决赛.
故选A.
5.C
【分析】
根据平均数、中位数、众数、方差的意义进行分析选择.
【详解】
解:平均数、中位数、众数是描述一组数据集中程度的统计量;方差、标准差是描述一组数据离散程度的统计量.既然是为筹备班级的初中毕业联欢会做准备,那么买的水果肯定是大多数人爱吃的才行,故最值得关注的是众数.
故选:C.
【点睛】
此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.
反映数据集中程度的平均数、中位数、众数各有局限性,因此要对统计量进行合理的选择和恰当的运用.
6.D
【分析】
由于众数是一组数据中出现次数最多的数据,注意众数可以不止一个,由此即可确定这组数据的众数.
【详解】
解:∵5是这组数据中出现次数最多的数据,
∴这组数据的众数为5.
故选D.
【点睛】
本题属于基础题,考查了确定一组数据的众数的能力,解题关键是要明确定义,读懂题意.
7.C
【分析】
直接利用众数的定义求解即可.
【详解】
解:由统计表可知,本次测试成绩中,90分的人数最多,有42人,所以本此测试成绩的众数为90分,
故选:C.
【点睛】
本题考查统计表、众数,理解众数的定义,能从统计表中获取有效信息是解答的关键.
8.C
【分析】
根据众数的含义:在一组数据中出现次数最多的数叫做这组数据的众数.
【详解】
在这组数据中6出现3次,次数最多,所以众数为6,故选C.
【点睛】
本题考查众数的定义,学生们熟练掌握即可解答.
9.B
【分析】
由折线统计图得出第二周的日最高气温重新排列为24、25、25、25、26、26、28,再根据众数的定义求解即可.
【详解】
解:由折线统计图知,第二周的日最高气温重新排列为24、25、25、25、26、26、28,
所以这周的日最高气温的众数是25,
故选:B.
【点睛】
本题主要考查众数和折线统计图,解题的关键是掌握众数的定义:一组数据中出现次数最多的数据叫做众数.
10.A
【分析】
根据众数的定义:一组数据中出现次数最多的数据为这组数据的众数;中位数的定义:将这组数据从小到大排列,若这组数据有奇数个数则最中间的数为中位数,若这组数据有偶数个数则中间的两个数的平均数为中位数.
【详解】
解:这组数据中18出现次数最多,即众数为18;
这组数据从小到大排列如下:14、14、15、16、16、16、17、17、17、17、17、17、18、18、18、18、18、18、18、18、19、19、19
则中位数为(17+17)÷2=17.
故选A.
【点睛】
本题主要考查了中位数和众数的求法,掌握正确中位数和众数得定义成为解答本题的关键.
11.C
【分析】
根据销售量统计图知,尺码为的该款运动鞋销量最多, 因而应多进些,这是众数的影响,因而可作出判断.
【详解】
由于尺码为的该款运动鞋销量最多,因而影响鞋店这一决策的统计量是众数
故选:C.
【点睛】
本题考查了众数这一统计量,一组数据中出现次数最多的数称为这组数据的众数,众数反映一组数据的集中趋势.
12.A
【分析】
方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
【详解】
∵小明五次成绩的平均数是90,方差是2;小强五次成绩的平均数也是90,方差是14.8.
平均成绩一样,小明的方差小,成绩稳定,
故选A.
【点睛】
本题考查方差、平均数的定义,解题的关键是熟练掌握基本知识,属于中考基础题.
错因分析 容易题.失分原因是方差的意义掌握不牢.
13.B
【分析】
根据平均数,方差的定义计算即可.
【详解】
解:∵小亮的成绩和其他39人的平均数相同,都是90分,
∴该班40人的测试成绩的平均分为90分,方差变小,
故选:B.
【点睛】
本题考查方差,算术平均数等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
14.D
【分析】
根据方差的意义:方差是反映一组数据波动大小,稳定程度的量;方差越大,表明这组数据偏离平均数越大,即波动越大,反之也成立.标准差是方差的平方根,也能反映数据的波动性;故要判断他的数学成绩是否稳定,那么老师需要知道他这5次数学考试成绩的方差.
【详解】
解:由于方差和标准差反映数据的波动性,要判断数学成绩是否稳定,需要知道他这5次数学考试成绩的方差或标准差.
故选:D.
【点睛】
本题考查了方差和标准差的意义.方差是用来衡量一组数据波动大小的量.
15.C
【分析】
根据平均数、众数、中位数及方差的计算方法进行判断即可得解.
【详解】
∵数据87变成90,
∴平均数发生变化,方差发生变化,A和D选项错误;
∵原来众数是92,87变成90后,
∴众数发生了变化,B选项错误;
∵这组数据的中位数第3个数据91,
∴将B玩具的重量写成了90克,不影响数据的中位数,
故选:C.
【点睛】
本题主要考查了平均数、众数、中位数、方差的计算,熟练掌握相关计算方法是解决本题的关键.
16.D
【分析】
结合题意,根据平均数和方差的性质,基于甲、乙、丙、丁四人射箭成绩平均数相同的情况下,方差最小的对应成绩最稳定,即可得到答案.
【详解】
根据题意,甲、乙、丙、丁四人射箭成绩的平均数都是8.9环,且丁的方差最小
∴射箭成绩最稳定的是丁
故选:D.
【点睛】
本题考查了方差、平均数的知识;解题的关键是熟练掌握平均数、方差的性质,并运用到实际问题中,从而完成求解.
17.D
【分析】
根据方差的意义求解即可.
【详解】
解:由表格知丁的方差最小,
所以这四名学生成绩最稳定的是丁,
故选:D.
【点睛】
本题主要考查方差,方差是反映一组数据的波动大小的一个量,方差越大,则与平均值的离散程度越大,稳定性越差;反之,则它与其平均值的离散程度越小,稳定性越好.
18.88
【详解】
试题分析:根据笔试和面试所占的百分比以及笔试成绩和面试成绩,列出算式,进行计算即可:
∵笔试按60%、面试按40%计算,
∴总成绩是:90×60%+85×40%=88(分).
19.88.8
【分析】
根据加权平均公式进行计算,即可得到答案.
【详解】
解:由题意,则该名教师的综合成绩为:
故答案为88.8
【点睛】
本题考查加权平均公式,解题的关键是掌握加权平均公式.
20.4
【分析】
根据众数的定义进行求解即可得.
【详解】
在这组数据中4出现次数最多,有3次,所以这组数据的众数为4,
故答案为4.
【点睛】
本题考查了众数,解题的关键是掌握求一组数据的众数的方法:找出频数最多的那个数据,若几个数据频数都是最多且相同,此时这几个数据都是众数.
21.甲
【详解】
试题分析:方差就是和中心偏离的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)在样本容量相同的情况下,方差越小,说明数据的波动越小,越稳定.因此,
∵,∴成绩比较稳定的是甲.
22.
【分析】
由一组数据4,x,2,3,6的平均数是4,可列方程:再解方程可得答案.
【详解】
解: 一组数据4,x,2,3,6的平均数是4,
故答案为:
【点睛】
本题考查的是平均数的含义,掌握平均数的计算是解题的关键.
23.乙
【分析】
方差越大,数据的波动越大;方差越小,数据的波动越小,根据方差的意义可得答案.
【详解】
解:∵1.8>1.3,
∴身高整齐的是乙班,
故答案为:乙.
【点睛】
本题主要考查方差,解题的关键是掌握方差的意义:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
24.84
【分析】
根据加权平均数的计算公式列出算式,再进行计算即可.
【详解】
解:该应聘者的最终成绩是:90807584(分).
故答案为:84.
【点睛】
此题考查了加权平均数,解题的关键是熟记加权平均数的计算方法.
25.16.7
【分析】
根据加权平均数的计算公式列出算式,再进行计算即可.
【详解】
解:他最终的得分是:18×+15×+16×=16.7(分).
故答案为:16.7.
【点睛】
本题考查了加权平均数的计算,掌握加权平均数的计算公式是解题的关键.
26.3
【分析】
根据平均数的计算方法,列出方程然后计算即可.
【详解】
解:∵数据:1,3,a,8,10的平均数是5,
∴=5,
解得a=3,
故答案为:3.
【点睛】
本题考查了平均数,正确理解平均数的意义是解题的关键.
27.24
【分析】
根据中位数的概念,即可求出答案.
【详解】
解:∵23个数据按照从小到大的顺序排列,第12个数据是24,
∴这23名队员年龄的中位数是24.
故答案为:24.
【点睛】
本题考查了中位数的概念,正确理解中位数的概念,把数据按顺序正确排列是解决问题的关键.
28.6
【分析】
根据题目中数据和题意,可以得到x的值,再根据中位数的定义求解即可.
【详解】
解:一组数据:-1,4,x,6,15的众数为6,
∴x=6,
这组数据按照从小到大排列是:
-1,4,6,6,15,
则这组数据的中位数是:6;
故答案为:6.
【点睛】
本题考查了众数、中位数的意义.众数是数据中出现最多的数;一组数据的中位数是先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.
29.(1)5;91;100 (2)1040人 (3)中位数:在统计的问卷的成绩中,最中间的两个分数的平均数是91分;众数:在统计的问卷的成绩中,得分的人数最多
【分析】
(1)用总人数减去已知人数即可得到a的值;将这20个数据按大小顺序排列,第10和11个数据的平均数即为中位数,出现次数最多的数据即为人数;
(2)先求出样本中不低于90分的人数所占样本的百分比,再乘以1600即可得到结果;
(3)根据中位数和众数的意义进行回答即可.
【详解】
(1)a=20-3-4-8=5;
将这组数据按大小顺序排列为:
81,82,83,86,87,88,89,90,90,90,92,93,96,96,98,99,100,100,100,100,
其中第10个和第11个数据分别是90,92,
所以,这组数据的中位数b=;
100出现了4次,出现的次数最多,所以,众数c是100;
(2),
(人)
(3)中位数:在统计的问卷的成绩中,最中间的两个分数的平均数是91分;
众数:在统计的问卷的成绩中,得分的人数最多.
【点睛】
本题主要考查了平均数、众数、中位数在实际问题中的正确应用,熟练掌握定义和计算公式是解题的关键.
30.(1)8为众数,7为中位数;(2)该同学所得分数的平均数为7.
【详解】
【分析】(1)根据众数与中位数的定义求解即可;
(2)根据平均数的定义求解即可.
【详解】(1)从小到大排列这组数据为:5,6,7,7,8,8,8,
数据8出现了三次最多为众数,
7处在第4位为中位数;
(2)该同学所得分数的平均数为(5+6+7×2+8×3)÷7=7.
【点睛】本题考查了平均数、众数与中位数,用到的知识点是:给定一组数据,出现次数最多的那个数,称为这组数据的众数.中位数的定义:将一组数据从小到大依次排列,把中间数据(或中间两数的平均数)叫做中位数.平均数=总数÷个数.
31.(1)30;(2)10,10;(3)这组数据的平均数为12元.
【分析】
(1)由各小组的频数之和可得出本次调查的人数;
(2)由众数和中位数的定义即可得出结果;
(3)由加权平均数公式即可得出结果.
【详解】
解:(1)本次调查的人数是6+11+8+5=30;
故答案为:30.
(2)这组数据中出现次数最多的是元,所以这组数据的众数为10元,
这组数据是按从小到大的顺序排列的,第个数据分别是,所以这组数据的中位数为元;
故答案为:10,10.
(3)这组数据的平均数为(元)
答:这组数据的平均数为12元.
【点睛】
本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.本题也考查了平均数、中位数、众数的定义,掌握以上知识是解题的关键.
32.(1)3;2;91;90;(2)估计评选该荣誉称号的人数为105人;(3)11月份开展的“防溺水知识应知应答”测评活动的效果比较好.
【分析】
由题意直接写出a,b的值,再根据中位数和众数的定义即可求出c,d的值;
(2)先求出测评成绩优秀的学生人数所占分率,再乘300即可得出结论.
(3)从中位数出发,结合题意即可得出结论;
【详解】
解:(1)由题意得:91分的有2个,即a=3;
98分的有2个,即b=2;
出现次数最多的是90分,故众数是90分,即d=90;
一共20个数据,第10个,第11个数据都是91,故中位数是91分,即c=91.
故答案为:3;2;91;90;
(2)300×=105(人).
答:估计评选该荣誉称号的人数为105人;
(3)10月份的中位数是91,11月份的中位数是93,
∵93>91,
∴ 11月份开展的“防溺水知识应知应答”测评活动的效果比较好.
【点睛】
本题考查了众数、平均数、中位数、用样本估计总体等知识;熟练掌握众数、平均数、中位数的定义以及用样本估计总体是解题的关键.
33.(1)9,9;(2);(3)推荐甲参加比赛合适.
【分析】
(1)根据中位数的定义先把这组数据从小到大排列,再找出最中间两个数的平均数即可求出①;根据平均数的计算公式即可求出②;
(2)根据方差的计算公式代值计算即可;
(3)根据方差的意义:反映了一组数据的波动大小,方差越大,波动性越大,反之也成立,即可得出答案.
【详解】
解:(1)甲的中位数是:;
乙的平均数是:(10+7+10+10+9+8)÷6=9;
故答案为9,9;
(2);
(3),
∴
∴推荐甲参加比赛合适.
【点睛】
本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为,则方差它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
34.(1)80;(2)众数是13岁,中位数是14岁;(3)984人
【分析】
(1)根据15岁的人数和所占的百分比求出样本容量;
(2)根据众数、中位数和平均数的定义分别进行解答即可;
(3)用总人数乘以年龄在14岁及以上的学生所占的百分比即可.
【详解】
解:(1)样本容量是:16÷20%=80;
(2)14岁的人数有:80 4 35 16=25(人),
∵13岁的有35人,人数最多,
∴众数是13岁;
把这些数从小大排列,中位数是第40、41个数的平均数,
则中位数是=14(岁);
(3)(人),
答:全校年龄在14岁及以上的学生大约有984人.
【点睛】
本题考查条形统计图、扇形统计图等知识,解题的关键是记住基本概念,属于中考常考题型.
35.(1)169、169、169;(2)甲;(3)选择甲,理由见解析
【分析】
( 1)利用平均数、众数及中位数的定义分别求得a、b、c的值即可;
(2)方差越大,波动性越大,成绩越不稳定,反之也成立;
( 3 )比较一下甲、乙两名跳高运动员进行了8次选拔比赛的成绩,看谁的成绩在1.65或1.65米以上的次数多,就选哪位运动员参赛;若成绩在1.70米可获得冠军,看谁的成绩在1.70或1.70米以上的次数多,就选哪位运动员参赛.
【详解】
(1).
.
∵169出现了3次,最多,
∴c=169.
故答案为169,169,169
(2)甲
∵甲的方差小于乙的方差,
∴甲的成绩更稳定,
故答案为:甲
(3)应选择甲.
理由如下:
若跳高1.65米就获得冠军,那么成绩在1.65或1.65米以上的次数甲多,则选择甲;
故答案为甲.
【点睛】
本题考查平均数和方差的意义,平均数表示数据的平均水平;方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定﹒
36.(1)5,80.5,81;(2)B;(3)13
【分析】
(1)用总人数减去A,,等级的人数即可求出a的值;根据中位数概念即可求出b的值;根据众数的概念即可求出c的值;
(2)根据平均数,中位数和众数即可得出该校学生每周用于课外阅读时间的等级;
(3)用阅读书籍的平均时间乘以一年的周数,再除以阅读每本书所需时间即可得.
【详解】
(1);
20名学生每周用于自主阅读的时间从小到大排列为如下:
10,30,30,44,50,60,60,75,80,80,81,81,81,92,100,110,120,130,140,146,
∵第10、11个数据分别为80、81,
∴中位数;
出现次数最多的数是81,
∴众数是81.
故答案为:5,80.5,81;
(2)∵平均数为80,中位数为80.5,众数为81,
∴用样本中的统计量估计该校学生每周用于课外阅读时间的等级为B;
故答案为:B;
(3)估计该校学生每人一年(按52周计算)平均阅读课外书为(本),
故答案为:13.
【点睛】
此题主要考查数据的统计和分析的知识.准确把握三数(平均数、中位数、众数)和理解样本和总体的关系是关键.
37.(1)88.5;(2)八年级,理由见解析;(3)126人
【分析】
(1)根据表格中的数据,可以求得n的值;
(2)根据表格中的数据,可以判断该生所在的年级,然后根据表格中的数据,即可说明理由;
(3)根据表格中的数据,可以计算出七年级成绩优秀的学生人数.
【详解】
解:(1)由表格中的数据可得,
n=(88+89)÷2=88.5,
故答案为:88.5;
(2)在学生样本成绩中,某学生的成绩是87分,在他所属年级抽取的学生中排在前10名,根据表中数据判断该学生所在年级是八年级,
理由:∵七年级中位数是88.5,87<88.5,
∴如果该学生在七年级,排名是后10名,不合题意;
∵八年级中位数是85,85<87,
∴如果该学生在八年级,排名是前10名,符合题意;
由上可得,在学生样本成绩中,某学生的成绩是87分,在他所属年级抽取的学生中排在前10名,根据表中数据判断该学生所在年级是八年级;
(3)180×=126(人),
答:七年级成绩优秀的学生有126人.
【点睛】
本题考查中位数和众数、用样本估计总体,解答本题的关键是明确题意,会求一组数据的中位数.
38.(1)见解析;(2)众数是20元,中位数是20元;(3)28800元.
【分析】
(1)先求出捐款为“30元”的人数,即可补全统计图;
(2)根据中位数、众数的意义分别进行计算即可;
(3)计算八年级一班班捐款的平均数,然后全校的人数乘以八年级一班班捐款的平均数,即可即可求解.
【详解】
解:(1)捐款为“30元”的人数:50﹣6﹣15﹣19﹣2=8(人),
补全条形统计图如下:
(2)八年级一班50名学生捐款金额出现次数最多的是20元,共出现19次,因此捐款的众数是20元,
将这50名学生捐款金额从小到大排列,处在中间位置的两个数都是20元,因此捐款金额的中位数是20元,
答:这组数据的众数是20元,中位数是20元;
(3)八年级一班捐款的平均数为:(元),
全校捐款总金额为:18×1600=28800(元),
答:全校1600学生共捐款约为28800元.
【点睛】
本题考查中位数、众数、平均数,掌握中位数、众数的定义是解决问题的关键,样本估计总体是统计中常用的方法.
39.(1)1,8,81,79;(2)120人;(3)八年级学生的总体水平较好,见解析
【分析】
(1)根据题目所给的数据即可求出a、b,然后根据中位数和众数的定义求出m、n即可;
(2)先算出样本中两个年级学生成绩在90分以上的人数占比,然后估计总体的即可;
(3)根据两个年级平均数相同,但是八年级的中位数比七年级的大,进行求解即可.
【详解】
解:(1)由题意可得:a的值为1,b的值为8,
∵八年级的20名学生成绩中成绩为81的出现了四次,出现的次数最多,
∴八年级的众数为81
∴m的值为81,
将七年级的20名学生的成绩排列如下:58,64,68,73,74,75,75,75,75,79,79,80,80,82,82,84, 85,85, 92, 95,
∵处在最中间的两个数分别为79、79,
∴七年级的中位数为,
∴n的值为79,
故答案为:1,8,81,79;
(2)由题意得(人).
(3)八年级学生的总体水平较好.
∵七、八年级的平均成绩相等,而八年级的中位数大于七年级的中位数,
∴八年级得分高的人数相对较多.
∴八年级学生的总体水平较好.
【点睛】
本题主要考查了中位数和众数,频数分布表,利用中位数判断成绩的好坏,解题的关键在于能够熟练掌握相关知识进行求解.
40.(1)85;86;(2)甲
【分析】
(1)根据算术平均数的定义求解即可;
(2)根据加权平均数的定义求解即可.
【详解】
解:(1)甲“三项测试”的平均成绩为=85(分),
乙“三项测试”的平均成绩为=86(分),
故答案为:85、86;
(2)甲的平均成绩为=86.5(分),
乙的平均成绩为=85.8(分),
∴应该录取甲.
【点睛】
本题主要考查加权平均数,解题的关键是掌握加权平均数和算术平均数的定义.
答案第1页,共2页
一、单选题
1.(2021·吉林经济技术开发区·八年级期末)若四个数据10,15,x,20的平均数是15,那么x的值为( )
A.10 B.20 C.15 D.25
2.(2021·吉林宽城·八年级期末)某校评选先进班集体,从“学习”、“卫生”、“纪律”、“活动参与”四个方面考核打分,各项满分均为,所占比例如下表:
项目 学习 卫生 纪律 活动参与
所占比例
八年级班这四项得分依次为,,,,则该班四项综合得分(满分)为( )
A. B. C. D.
3.(2021·吉林铁西·八年级期末)在庆祝新中国成立70周年的校园歌唱比赛中,11名参赛同学的成绩各不相同,按照成绩取前5名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这11名同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
4.(2021·吉林伊通·八年级期末)某校七年级有13名同学参加百米竞赛,预赛成绩各不相同,要取前6名参加决赛,小梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这13名同学成绩的( )
A.中位数 B.众数 C.平均数 D.极差
5.(2021·吉林德惠·八年级期末)为筹备班级联欢会,班长对全班同学爱吃哪几种水果做了民意调查,然后决定买什么水果,最值得关注的应该是统计调查数据的( )
A.中位数 B.平均数 C.众数 D.方差
6.(2021·吉林靖宇·八年级期末)数据2,3,5,5,4的众数是( ).
A.2 B.3 C.4 D.5
7.(2021·吉林梅河口·八年级期末)每年的6月5日为世界环境保护日,为提高学生环境保护意识,某校对100名学生进行“保护环境知多少”测试,抽取部分统计如下表:
成绩(分) 60 70 80 90 100
人数(人) 7 20 23 42 8
本次测验成绩的众数为( )
A.80分 B.85分 C.90分 D.100分
8.(2021·吉林双辽·八年级期末)一组数据8,7,6,7,6,5,4,5,8,6的众数是( )
A.8 B.7 C.6 D.5
9.(2021·吉林吉林·八年级期末)如图,给出了吉林市2021年6月份第二周的日最高气温,则这周的日最高气温的众数是( )
A.24 B.25 C.26 D.28
10.(2021·吉林大安·八年级期末)某校男子足球队22名队员的年龄如下表所示:
年龄/岁 14 15 16 17 18 19
人数 2 1 3 6 7 3
这些队员年龄的众数和中位数分别是( )
A.18,17 B.17,18 C.18,17.5 D.17.5,18
11.(2021·吉林·八年级期末)一家鞋店在一段时间内销售了某款运动鞋30双,该款的各种尺码鞋销售量如图所示.鞋店决定在下一次进货时增加一些尺码为的该款运动鞋,影响鞋店这一决策的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
12.(2021·吉林朝阳·八年级期末)为参加学校举办的“诗意校园 致远方”朗诵艺术大赛,八年级“屈原读书社”组织了五次选拔赛,这五次选拔赛中,小明五次成绩的平均数是90,方差是2;小强五次成绩的平均数也是90,方差是14.8.下列说法正确的是( )
A.小明的成绩比小强稳定
B.小明、小强两人成绩一样稳定
C.小强的成绩比小明稳定
D.无法确定小明、小强的成绩谁更稳定
13.(2021·吉林桦甸·八年级期末)某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )
A.平均分不变,方差变大 B.平均分不变,方差变小
C.平均分和方差都不变 D.平均分和方差都改变
14.(2021·吉林双阳·八年级期末)数学老师对小明的5次单元测验成绩进行统计分析,要判断小明的数学成绩是否稳定,老师需要知道小明这5次数学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
15.(2021·吉林德惠·八年级期末)某玩具厂质检员对A,B,C,D,E这5个玩具进行称重,实际重量分别为:90,87,92,92,91(单位:克).在统计时,不小心将B玩具的重量写成了90克,则计算结果不受影响的是( )
A.平均数 B.众数 C.中位数 D.方差
16.(2021·吉林·舒兰市教师进修学校八年级期末)甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均数都是8.9环,方差分别是,,,,则射箭成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
17.(2021·吉林汽车经济技术开发区·八年级期末)甲、乙、丙、丁四名学生近4次数学成绩的平均数都是108分,方差如下表,则这四名学生成绩最稳定的是( )
学生 甲 乙 丙 丁
方差(s2) 86 51.5 63.5 19.5
A.甲 B.乙 C.丙 D.丁
二、填空题
18.(2021·吉林靖宇·八年级期末)某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是_____分.
19.(2021·吉林桦甸·八年级期末)某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试得分分别为92分、85分、90分,综合成绩笔试占40%,试讲占40%,面试占20%,则该名教师的综合成绩为_______分.
20.(2021·吉林农安·八年级期末)一组数3,4,7,4,3,4,5,6,5的众数是_____.
21.(2021·吉林大安·八年级期末)甲、乙两名射击手的50次测试的平均成绩都是8环,方差分别是,则成绩比较稳定的是___(填“甲”或“乙”)
22.(2021·吉林·八年级期末)如果一组数据4,x,2,3,6的平均数是4,那么x是_____.
23.(2021·吉林双辽·八年级期末)在学校团体操比赛中,甲、乙两个班的同学身高的平均数相同,方差分别是 ,,那么身高整齐的是_____班.
24.(2021·吉林南关·八年级期末)某公司决定招聘广告策划人员一人,某应聘者三项素质测试的成绩(单位:分)如下:
测试项目 创新能力 综合知识 语言表达
测试成绩 90 80 75
如果将创新能力、综合能力和语言表达三项素质测试成绩按的比确定应聘者的最终成绩,则应聘者的最终成绩为______分.
25.(2021·吉林汽车经济技术开发区·八年级期末)小明在参加岗位应聘中,专业知识、工作经验、仪表形象三项的得分分别为:18分、15分、16分.若这三项的重要性之比为5:3:2,则他最终的得分是 _______分.
26.(2021·吉林铁西·八年级期末)已知一组数据:1,3,a,8,10的平均数是5,则a=___.
27.(2021·吉林吉林·八年级期末)某足球队23名队员年龄情况如表所示,这23名队员年龄的中位数是______.
年龄(岁) 21 22 23 24 25 26
人数 2 4 5 6 4 2
28.(2021·吉林经济技术开发区·八年级期末)已知一组数据-1,4,x,6,15的众数为6,那么这组数据的中位数是____.
三、解答题
29.(2021·吉林大安·八年级期末)小手拉大手,共创文明城.某校为了了解家长对南宁市创建全国文明城市相关知识的知晓情况,通过发放问卷进行测评,从中随机抽取份答卷,并统计成绩(成绩得分用表示,单位:分),收集数据如下:
整理数据:
分析数据:
平均分 中位数 众数
根据以上信息,解答下列问题:
(1)直接写出上述表格中的值;
(2)该校有名家长参加了此次问卷测评活动,请估计成绩不低于分的人数是多少?
(3)请从中位数和众数中选择一个量, 结合本题解释它的意义.
30.(2021·吉林农安·八年级期末)某同学参加了学校举行的“五好小公民 红旗飘飘”演讲比赛,7名评委给该同学的打分(单位:分)情况如下表:
评委 评委1 评委2 评委3 评委4 评委5 评委6 评委7
打分 6 8 7 8 5 7 8
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数
31.(2021·吉林双辽·八年级期末)在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成如图所示的统计图.
(1)本次调查的人数是 ;
(2)这组数据的众数为 元,中位数为 元;
(3)求这组数据的平均数.
32.(2021·吉林德惠·八年级期末)为了加强安全教育,某校对学生进行“防溺水知识应知应答”测评.该校随机选取了八年级300名学生中的20名学生在10月份测评的成绩,数据如下:
收集数据:
97 91 89 95 90 99 90 97 91 98
90 90 91 88 98 97 95 90 96 88
整理、描述数据:
成绩/分 88 89 90 91 95 96 97 98 99
学生人数 2 1 5 2 1 3 1
数据分析:样本数据的平均数、众数和中位数如表:
平均数 中位数 众数
93
(1) , , , ;
(2)该校决定授予在10月份测评成绩优秀(96分及以上)的八年级的学生“防溺水小卫士”荣誉称号,请估计评选该荣誉称号的人数.
(3)若被选取的20名学生在11月份测评的成绩的平均数、众数和中位数如表:
平均数 中位数 众数
95 93 94
结合相关数据,从一个方面评价10月份到11月份开展的“防溺水知识应知应答”测评活动的效果.
33.(2021·吉林前郭尔罗斯·八年级期末)射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 第二次 第三次 第四次 第五次 第六次 平均成绩 中位数
甲 10 8 9 8 10 9 9 ①
乙 10 7 10 10 9 8 ② 9.5
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为,你认为推荐谁参加比赛更合适,请说明理由.
34.(2021·吉林铁西·八年级期末)我校小李同学对北大附中初中三个年级的学生年龄构成很感兴趣,整理数据并绘制如图所示不完整的统计图.依据信息解答下列问题.
(1)求样本容量;
(2)直接写出样本数据的众数、中位数;
(3)已知北大附中实验学校一共有1920名学生,请估计全校年龄在14岁及以上的学生大约有多少人.
35.(2021·吉林宽城·八年级期末)某校拟派一名跳高运动员参加校际比赛,对甲、乙两名同学进行了8次跳高选拔比赛,他们的原始成绩(单位:cm)如下表:
次数 成绩 学生 第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次
甲 169 165 168 169 172 173 169 167
乙 161 174 172 162 163 172 172 176
两名同学的8次跳高成绩数据分析如下表:
名称 成绩 学生 平均数 (单位:cm) 中位数 (单位:cm) 众数 (单位:cm) 方差 (单位:cm2)
甲 a b c 5.75
乙 169 172 172 31.25
根据图表信息回答下列问题:
(1)求a、b、c的值.
(2)这两名同学中, 的成绩更为稳定(填“甲”或“乙”).
(3)若预测跳高165cm就可能获得冠军,该校为了获取跳高比赛冠军,你认为应该选择哪位同学参赛,并说明理由
36.(2021·吉林桦甸·八年级期末)在新冠状病毒防控期间,各地纷纷展开了停课不停学活动,学校为了了解学生自主阅读情况,抽样调查了部分学生每周用于自主阅读的时间,过程如下:
收集数据:
从全校随机抽取20名学生,每周用于自主阅读时间的调查,数据如下:(单位:)
30 60 81 50 44 110 130 146 80 100
60 80 120 140 75 81 10 30 81 92
整理数据:按下表分段整理样本数据:
自主阅读时间
等级 A
人数 3 8 4
分析数据:样本的平均数、中位数、众数如下表所示:
平均数 中位数 众数
80
请回答下列问题:
(1)表格中的数据_______,________,_______;
(2)用样本中的统计量估计该校学生每周用于课外阅读时间的等级为______;
(3)假设平均阅读一本课外书的时间为320分钟,请你用样本平均数估计该校学生每人一年(按52周计算)平均阅读________本课外书.
37.(2021·吉林汽车经济技术开发区·八年级期末)第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,某校对七、八年级全体学生进行了相关知识测试,然后从七、八年级各随机抽取了20名学生的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
Ⅰ.七年级20名学生成绩的频数分布表如下:
七年级学生样本成绩频数分布表
成绩m(分) 频数(人数)
50≤m<60 1
60≤m<70 2
70≤m<80 3
80≤m<90 8
90≤m≤100 6
合计 20
Ⅱ.七年级20名学生成绩在80≤m<90这一组的具体成绩是:
87 88 88 88 89 89 89 89
Ⅲ.七、八年级学生样本成绩的平均数、中位数、众数如下表所示:
平均数 中位数 众数
七年级 84 n 89
八年级 84.2 85 85
根据以上提供的信息,解答下列问题:
(1)表中n的值为 .
(2)在学生样本成绩中,某学生的成绩是87分,在他所属年级抽取的学生中排在前10名,根据表中数据判断该学生所在年级,并说明理由.
(3)七年级共有学生180名,若将不低于80分的成绩定为优秀,请估计七年级成绩优秀的学生人数.
38.(2021·吉林伊通·八年级期末)2013年我省松原地震后,某中学开展了“我为灾区献爱心”捐款活动,八年级一班的团支部对全班50人捐款数额进行了统计,并绘制了下面统计图.
(1)把统计图补充完整;
(2)直接写出这组数据的众数和中位数;
(3)该校共有学生1600人,请你根据八年级一班的捐款情况,估计该中学的捐款总数.
39.(2021·吉林南关·八年级期末)每年的4月15日是我国全民国家安全教育日,某中学在全校七、八年级学生中开展了“国家安全法”知识竞赛.为了解七、八年级学生对“国家安全法”知识的掌握情况,现从七、八年级各随机抽取20名学生的竞赛成绩(百分制),分数如下:
七年级:82,58,73,80,75,74,85,64,75,95,75,79,82,68,75,80,92,85,84,79
八年级:92,72,90,81,72,81,93,82,78,83,80,81,71,81,72,77,82,80,70,41
对以上数据进行整理分析,得到下列表一和表二:
表一
七年级 0 2 7 2
八年级 1 0 0 7 9 3
表二
平均数 众数 中位数
七年级 78
八年级 78 80.5
根据以上信息,解答下列问题:
(1)的值为 ,的值为 ,的值为 ,的值为 .
(2)若该校七、八年级各有600人,估计该校七、八年级在本次竞赛成绩在90分以上的共有多少人.
(3)你认为哪个年级学生对“国家安全法”知识掌握的总体水平较好?请说明理由.
40.(2021·吉林吉林·八年级期末)某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表:(单位:分)
项目 选手 阅读能力 思维能力 表达能力
甲 94 87 74
乙 96 82 80
(1)甲、乙两人“三项测试”的平均成绩分别为 分、 分;
(2)根据实际需要,公司将阅读能力、思维能力和表达能力三项测试成绩按3:5:2的比确定每位应聘者的成绩,请你计算甲、乙两人的平均成绩,从他们的成绩看,应该录取谁?
试卷第1页,共3页
参考答案:
1.C
【分析】
运用平均数的计算公式即可求得的值.
【详解】
解:根据题意知,
解得:,
故选:C.
【点睛】
本题考查了算术平均数的求法.熟记公式是解决本题的关键.
2.B
【分析】
根据加权平均数的定义计算可得.
【详解】
解:80×40%+90×25%+84×25%+70×10%=82.5(分)
故选:B
【点睛】
本题主要考查平均数,解题的关键是掌握算术平均数和加权平均数的定义.
3.B
【分析】
由于比赛取前5名参加决赛,共有11名选手参加,根据中位数的意义分析即可.
【详解】
11个不同的成绩按从小到大排序后,中位数及中位数之后的共有5个数,
故只要知道自己的成绩和中位数就可以知道是否进入决赛了.
故选B.
【点睛】
本题考查了中位数意义.解题的关键是正确的求出这组数据的中位数.
4.A
【详解】
共有13名学生参加竞赛,取前6名,所以小梅需要知道自己的成绩是否进入前六.我们把所有同学的成绩按大小顺序排列,第7名学生的成绩是这组数据的中位数,所以小梅知道这组数据的中位数,才能知道自己是否进入决赛.
故选A.
5.C
【分析】
根据平均数、中位数、众数、方差的意义进行分析选择.
【详解】
解:平均数、中位数、众数是描述一组数据集中程度的统计量;方差、标准差是描述一组数据离散程度的统计量.既然是为筹备班级的初中毕业联欢会做准备,那么买的水果肯定是大多数人爱吃的才行,故最值得关注的是众数.
故选:C.
【点睛】
此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.
反映数据集中程度的平均数、中位数、众数各有局限性,因此要对统计量进行合理的选择和恰当的运用.
6.D
【分析】
由于众数是一组数据中出现次数最多的数据,注意众数可以不止一个,由此即可确定这组数据的众数.
【详解】
解:∵5是这组数据中出现次数最多的数据,
∴这组数据的众数为5.
故选D.
【点睛】
本题属于基础题,考查了确定一组数据的众数的能力,解题关键是要明确定义,读懂题意.
7.C
【分析】
直接利用众数的定义求解即可.
【详解】
解:由统计表可知,本次测试成绩中,90分的人数最多,有42人,所以本此测试成绩的众数为90分,
故选:C.
【点睛】
本题考查统计表、众数,理解众数的定义,能从统计表中获取有效信息是解答的关键.
8.C
【分析】
根据众数的含义:在一组数据中出现次数最多的数叫做这组数据的众数.
【详解】
在这组数据中6出现3次,次数最多,所以众数为6,故选C.
【点睛】
本题考查众数的定义,学生们熟练掌握即可解答.
9.B
【分析】
由折线统计图得出第二周的日最高气温重新排列为24、25、25、25、26、26、28,再根据众数的定义求解即可.
【详解】
解:由折线统计图知,第二周的日最高气温重新排列为24、25、25、25、26、26、28,
所以这周的日最高气温的众数是25,
故选:B.
【点睛】
本题主要考查众数和折线统计图,解题的关键是掌握众数的定义:一组数据中出现次数最多的数据叫做众数.
10.A
【分析】
根据众数的定义:一组数据中出现次数最多的数据为这组数据的众数;中位数的定义:将这组数据从小到大排列,若这组数据有奇数个数则最中间的数为中位数,若这组数据有偶数个数则中间的两个数的平均数为中位数.
【详解】
解:这组数据中18出现次数最多,即众数为18;
这组数据从小到大排列如下:14、14、15、16、16、16、17、17、17、17、17、17、18、18、18、18、18、18、18、18、19、19、19
则中位数为(17+17)÷2=17.
故选A.
【点睛】
本题主要考查了中位数和众数的求法,掌握正确中位数和众数得定义成为解答本题的关键.
11.C
【分析】
根据销售量统计图知,尺码为的该款运动鞋销量最多, 因而应多进些,这是众数的影响,因而可作出判断.
【详解】
由于尺码为的该款运动鞋销量最多,因而影响鞋店这一决策的统计量是众数
故选:C.
【点睛】
本题考查了众数这一统计量,一组数据中出现次数最多的数称为这组数据的众数,众数反映一组数据的集中趋势.
12.A
【分析】
方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
【详解】
∵小明五次成绩的平均数是90,方差是2;小强五次成绩的平均数也是90,方差是14.8.
平均成绩一样,小明的方差小,成绩稳定,
故选A.
【点睛】
本题考查方差、平均数的定义,解题的关键是熟练掌握基本知识,属于中考基础题.
错因分析 容易题.失分原因是方差的意义掌握不牢.
13.B
【分析】
根据平均数,方差的定义计算即可.
【详解】
解:∵小亮的成绩和其他39人的平均数相同,都是90分,
∴该班40人的测试成绩的平均分为90分,方差变小,
故选:B.
【点睛】
本题考查方差,算术平均数等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
14.D
【分析】
根据方差的意义:方差是反映一组数据波动大小,稳定程度的量;方差越大,表明这组数据偏离平均数越大,即波动越大,反之也成立.标准差是方差的平方根,也能反映数据的波动性;故要判断他的数学成绩是否稳定,那么老师需要知道他这5次数学考试成绩的方差.
【详解】
解:由于方差和标准差反映数据的波动性,要判断数学成绩是否稳定,需要知道他这5次数学考试成绩的方差或标准差.
故选:D.
【点睛】
本题考查了方差和标准差的意义.方差是用来衡量一组数据波动大小的量.
15.C
【分析】
根据平均数、众数、中位数及方差的计算方法进行判断即可得解.
【详解】
∵数据87变成90,
∴平均数发生变化,方差发生变化,A和D选项错误;
∵原来众数是92,87变成90后,
∴众数发生了变化,B选项错误;
∵这组数据的中位数第3个数据91,
∴将B玩具的重量写成了90克,不影响数据的中位数,
故选:C.
【点睛】
本题主要考查了平均数、众数、中位数、方差的计算,熟练掌握相关计算方法是解决本题的关键.
16.D
【分析】
结合题意,根据平均数和方差的性质,基于甲、乙、丙、丁四人射箭成绩平均数相同的情况下,方差最小的对应成绩最稳定,即可得到答案.
【详解】
根据题意,甲、乙、丙、丁四人射箭成绩的平均数都是8.9环,且丁的方差最小
∴射箭成绩最稳定的是丁
故选:D.
【点睛】
本题考查了方差、平均数的知识;解题的关键是熟练掌握平均数、方差的性质,并运用到实际问题中,从而完成求解.
17.D
【分析】
根据方差的意义求解即可.
【详解】
解:由表格知丁的方差最小,
所以这四名学生成绩最稳定的是丁,
故选:D.
【点睛】
本题主要考查方差,方差是反映一组数据的波动大小的一个量,方差越大,则与平均值的离散程度越大,稳定性越差;反之,则它与其平均值的离散程度越小,稳定性越好.
18.88
【详解】
试题分析:根据笔试和面试所占的百分比以及笔试成绩和面试成绩,列出算式,进行计算即可:
∵笔试按60%、面试按40%计算,
∴总成绩是:90×60%+85×40%=88(分).
19.88.8
【分析】
根据加权平均公式进行计算,即可得到答案.
【详解】
解:由题意,则该名教师的综合成绩为:
故答案为88.8
【点睛】
本题考查加权平均公式,解题的关键是掌握加权平均公式.
20.4
【分析】
根据众数的定义进行求解即可得.
【详解】
在这组数据中4出现次数最多,有3次,所以这组数据的众数为4,
故答案为4.
【点睛】
本题考查了众数,解题的关键是掌握求一组数据的众数的方法:找出频数最多的那个数据,若几个数据频数都是最多且相同,此时这几个数据都是众数.
21.甲
【详解】
试题分析:方差就是和中心偏离的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)在样本容量相同的情况下,方差越小,说明数据的波动越小,越稳定.因此,
∵,∴成绩比较稳定的是甲.
22.
【分析】
由一组数据4,x,2,3,6的平均数是4,可列方程:再解方程可得答案.
【详解】
解: 一组数据4,x,2,3,6的平均数是4,
故答案为:
【点睛】
本题考查的是平均数的含义,掌握平均数的计算是解题的关键.
23.乙
【分析】
方差越大,数据的波动越大;方差越小,数据的波动越小,根据方差的意义可得答案.
【详解】
解:∵1.8>1.3,
∴身高整齐的是乙班,
故答案为:乙.
【点睛】
本题主要考查方差,解题的关键是掌握方差的意义:方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
24.84
【分析】
根据加权平均数的计算公式列出算式,再进行计算即可.
【详解】
解:该应聘者的最终成绩是:90807584(分).
故答案为:84.
【点睛】
此题考查了加权平均数,解题的关键是熟记加权平均数的计算方法.
25.16.7
【分析】
根据加权平均数的计算公式列出算式,再进行计算即可.
【详解】
解:他最终的得分是:18×+15×+16×=16.7(分).
故答案为:16.7.
【点睛】
本题考查了加权平均数的计算,掌握加权平均数的计算公式是解题的关键.
26.3
【分析】
根据平均数的计算方法,列出方程然后计算即可.
【详解】
解:∵数据:1,3,a,8,10的平均数是5,
∴=5,
解得a=3,
故答案为:3.
【点睛】
本题考查了平均数,正确理解平均数的意义是解题的关键.
27.24
【分析】
根据中位数的概念,即可求出答案.
【详解】
解:∵23个数据按照从小到大的顺序排列,第12个数据是24,
∴这23名队员年龄的中位数是24.
故答案为:24.
【点睛】
本题考查了中位数的概念,正确理解中位数的概念,把数据按顺序正确排列是解决问题的关键.
28.6
【分析】
根据题目中数据和题意,可以得到x的值,再根据中位数的定义求解即可.
【详解】
解:一组数据:-1,4,x,6,15的众数为6,
∴x=6,
这组数据按照从小到大排列是:
-1,4,6,6,15,
则这组数据的中位数是:6;
故答案为:6.
【点睛】
本题考查了众数、中位数的意义.众数是数据中出现最多的数;一组数据的中位数是先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.
29.(1)5;91;100 (2)1040人 (3)中位数:在统计的问卷的成绩中,最中间的两个分数的平均数是91分;众数:在统计的问卷的成绩中,得分的人数最多
【分析】
(1)用总人数减去已知人数即可得到a的值;将这20个数据按大小顺序排列,第10和11个数据的平均数即为中位数,出现次数最多的数据即为人数;
(2)先求出样本中不低于90分的人数所占样本的百分比,再乘以1600即可得到结果;
(3)根据中位数和众数的意义进行回答即可.
【详解】
(1)a=20-3-4-8=5;
将这组数据按大小顺序排列为:
81,82,83,86,87,88,89,90,90,90,92,93,96,96,98,99,100,100,100,100,
其中第10个和第11个数据分别是90,92,
所以,这组数据的中位数b=;
100出现了4次,出现的次数最多,所以,众数c是100;
(2),
(人)
(3)中位数:在统计的问卷的成绩中,最中间的两个分数的平均数是91分;
众数:在统计的问卷的成绩中,得分的人数最多.
【点睛】
本题主要考查了平均数、众数、中位数在实际问题中的正确应用,熟练掌握定义和计算公式是解题的关键.
30.(1)8为众数,7为中位数;(2)该同学所得分数的平均数为7.
【详解】
【分析】(1)根据众数与中位数的定义求解即可;
(2)根据平均数的定义求解即可.
【详解】(1)从小到大排列这组数据为:5,6,7,7,8,8,8,
数据8出现了三次最多为众数,
7处在第4位为中位数;
(2)该同学所得分数的平均数为(5+6+7×2+8×3)÷7=7.
【点睛】本题考查了平均数、众数与中位数,用到的知识点是:给定一组数据,出现次数最多的那个数,称为这组数据的众数.中位数的定义:将一组数据从小到大依次排列,把中间数据(或中间两数的平均数)叫做中位数.平均数=总数÷个数.
31.(1)30;(2)10,10;(3)这组数据的平均数为12元.
【分析】
(1)由各小组的频数之和可得出本次调查的人数;
(2)由众数和中位数的定义即可得出结果;
(3)由加权平均数公式即可得出结果.
【详解】
解:(1)本次调查的人数是6+11+8+5=30;
故答案为:30.
(2)这组数据中出现次数最多的是元,所以这组数据的众数为10元,
这组数据是按从小到大的顺序排列的,第个数据分别是,所以这组数据的中位数为元;
故答案为:10,10.
(3)这组数据的平均数为(元)
答:这组数据的平均数为12元.
【点睛】
本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.本题也考查了平均数、中位数、众数的定义,掌握以上知识是解题的关键.
32.(1)3;2;91;90;(2)估计评选该荣誉称号的人数为105人;(3)11月份开展的“防溺水知识应知应答”测评活动的效果比较好.
【分析】
由题意直接写出a,b的值,再根据中位数和众数的定义即可求出c,d的值;
(2)先求出测评成绩优秀的学生人数所占分率,再乘300即可得出结论.
(3)从中位数出发,结合题意即可得出结论;
【详解】
解:(1)由题意得:91分的有2个,即a=3;
98分的有2个,即b=2;
出现次数最多的是90分,故众数是90分,即d=90;
一共20个数据,第10个,第11个数据都是91,故中位数是91分,即c=91.
故答案为:3;2;91;90;
(2)300×=105(人).
答:估计评选该荣誉称号的人数为105人;
(3)10月份的中位数是91,11月份的中位数是93,
∵93>91,
∴ 11月份开展的“防溺水知识应知应答”测评活动的效果比较好.
【点睛】
本题考查了众数、平均数、中位数、用样本估计总体等知识;熟练掌握众数、平均数、中位数的定义以及用样本估计总体是解题的关键.
33.(1)9,9;(2);(3)推荐甲参加比赛合适.
【分析】
(1)根据中位数的定义先把这组数据从小到大排列,再找出最中间两个数的平均数即可求出①;根据平均数的计算公式即可求出②;
(2)根据方差的计算公式代值计算即可;
(3)根据方差的意义:反映了一组数据的波动大小,方差越大,波动性越大,反之也成立,即可得出答案.
【详解】
解:(1)甲的中位数是:;
乙的平均数是:(10+7+10+10+9+8)÷6=9;
故答案为9,9;
(2);
(3),
∴
∴推荐甲参加比赛合适.
【点睛】
本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为,则方差它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
34.(1)80;(2)众数是13岁,中位数是14岁;(3)984人
【分析】
(1)根据15岁的人数和所占的百分比求出样本容量;
(2)根据众数、中位数和平均数的定义分别进行解答即可;
(3)用总人数乘以年龄在14岁及以上的学生所占的百分比即可.
【详解】
解:(1)样本容量是:16÷20%=80;
(2)14岁的人数有:80 4 35 16=25(人),
∵13岁的有35人,人数最多,
∴众数是13岁;
把这些数从小大排列,中位数是第40、41个数的平均数,
则中位数是=14(岁);
(3)(人),
答:全校年龄在14岁及以上的学生大约有984人.
【点睛】
本题考查条形统计图、扇形统计图等知识,解题的关键是记住基本概念,属于中考常考题型.
35.(1)169、169、169;(2)甲;(3)选择甲,理由见解析
【分析】
( 1)利用平均数、众数及中位数的定义分别求得a、b、c的值即可;
(2)方差越大,波动性越大,成绩越不稳定,反之也成立;
( 3 )比较一下甲、乙两名跳高运动员进行了8次选拔比赛的成绩,看谁的成绩在1.65或1.65米以上的次数多,就选哪位运动员参赛;若成绩在1.70米可获得冠军,看谁的成绩在1.70或1.70米以上的次数多,就选哪位运动员参赛.
【详解】
(1).
.
∵169出现了3次,最多,
∴c=169.
故答案为169,169,169
(2)甲
∵甲的方差小于乙的方差,
∴甲的成绩更稳定,
故答案为:甲
(3)应选择甲.
理由如下:
若跳高1.65米就获得冠军,那么成绩在1.65或1.65米以上的次数甲多,则选择甲;
故答案为甲.
【点睛】
本题考查平均数和方差的意义,平均数表示数据的平均水平;方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定﹒
36.(1)5,80.5,81;(2)B;(3)13
【分析】
(1)用总人数减去A,,等级的人数即可求出a的值;根据中位数概念即可求出b的值;根据众数的概念即可求出c的值;
(2)根据平均数,中位数和众数即可得出该校学生每周用于课外阅读时间的等级;
(3)用阅读书籍的平均时间乘以一年的周数,再除以阅读每本书所需时间即可得.
【详解】
(1);
20名学生每周用于自主阅读的时间从小到大排列为如下:
10,30,30,44,50,60,60,75,80,80,81,81,81,92,100,110,120,130,140,146,
∵第10、11个数据分别为80、81,
∴中位数;
出现次数最多的数是81,
∴众数是81.
故答案为:5,80.5,81;
(2)∵平均数为80,中位数为80.5,众数为81,
∴用样本中的统计量估计该校学生每周用于课外阅读时间的等级为B;
故答案为:B;
(3)估计该校学生每人一年(按52周计算)平均阅读课外书为(本),
故答案为:13.
【点睛】
此题主要考查数据的统计和分析的知识.准确把握三数(平均数、中位数、众数)和理解样本和总体的关系是关键.
37.(1)88.5;(2)八年级,理由见解析;(3)126人
【分析】
(1)根据表格中的数据,可以求得n的值;
(2)根据表格中的数据,可以判断该生所在的年级,然后根据表格中的数据,即可说明理由;
(3)根据表格中的数据,可以计算出七年级成绩优秀的学生人数.
【详解】
解:(1)由表格中的数据可得,
n=(88+89)÷2=88.5,
故答案为:88.5;
(2)在学生样本成绩中,某学生的成绩是87分,在他所属年级抽取的学生中排在前10名,根据表中数据判断该学生所在年级是八年级,
理由:∵七年级中位数是88.5,87<88.5,
∴如果该学生在七年级,排名是后10名,不合题意;
∵八年级中位数是85,85<87,
∴如果该学生在八年级,排名是前10名,符合题意;
由上可得,在学生样本成绩中,某学生的成绩是87分,在他所属年级抽取的学生中排在前10名,根据表中数据判断该学生所在年级是八年级;
(3)180×=126(人),
答:七年级成绩优秀的学生有126人.
【点睛】
本题考查中位数和众数、用样本估计总体,解答本题的关键是明确题意,会求一组数据的中位数.
38.(1)见解析;(2)众数是20元,中位数是20元;(3)28800元.
【分析】
(1)先求出捐款为“30元”的人数,即可补全统计图;
(2)根据中位数、众数的意义分别进行计算即可;
(3)计算八年级一班班捐款的平均数,然后全校的人数乘以八年级一班班捐款的平均数,即可即可求解.
【详解】
解:(1)捐款为“30元”的人数:50﹣6﹣15﹣19﹣2=8(人),
补全条形统计图如下:
(2)八年级一班50名学生捐款金额出现次数最多的是20元,共出现19次,因此捐款的众数是20元,
将这50名学生捐款金额从小到大排列,处在中间位置的两个数都是20元,因此捐款金额的中位数是20元,
答:这组数据的众数是20元,中位数是20元;
(3)八年级一班捐款的平均数为:(元),
全校捐款总金额为:18×1600=28800(元),
答:全校1600学生共捐款约为28800元.
【点睛】
本题考查中位数、众数、平均数,掌握中位数、众数的定义是解决问题的关键,样本估计总体是统计中常用的方法.
39.(1)1,8,81,79;(2)120人;(3)八年级学生的总体水平较好,见解析
【分析】
(1)根据题目所给的数据即可求出a、b,然后根据中位数和众数的定义求出m、n即可;
(2)先算出样本中两个年级学生成绩在90分以上的人数占比,然后估计总体的即可;
(3)根据两个年级平均数相同,但是八年级的中位数比七年级的大,进行求解即可.
【详解】
解:(1)由题意可得:a的值为1,b的值为8,
∵八年级的20名学生成绩中成绩为81的出现了四次,出现的次数最多,
∴八年级的众数为81
∴m的值为81,
将七年级的20名学生的成绩排列如下:58,64,68,73,74,75,75,75,75,79,79,80,80,82,82,84, 85,85, 92, 95,
∵处在最中间的两个数分别为79、79,
∴七年级的中位数为,
∴n的值为79,
故答案为:1,8,81,79;
(2)由题意得(人).
(3)八年级学生的总体水平较好.
∵七、八年级的平均成绩相等,而八年级的中位数大于七年级的中位数,
∴八年级得分高的人数相对较多.
∴八年级学生的总体水平较好.
【点睛】
本题主要考查了中位数和众数,频数分布表,利用中位数判断成绩的好坏,解题的关键在于能够熟练掌握相关知识进行求解.
40.(1)85;86;(2)甲
【分析】
(1)根据算术平均数的定义求解即可;
(2)根据加权平均数的定义求解即可.
【详解】
解:(1)甲“三项测试”的平均成绩为=85(分),
乙“三项测试”的平均成绩为=86(分),
故答案为:85、86;
(2)甲的平均成绩为=86.5(分),
乙的平均成绩为=85.8(分),
∴应该录取甲.
【点睛】
本题主要考查加权平均数,解题的关键是掌握加权平均数和算术平均数的定义.
答案第1页,共2页
