第十章数据的收集、整理与描述练习题2020-2021学年吉林省部分地区七年级下学期人教版数学期末试题选编(Word版含解析)
文档属性
| 名称 | 第十章数据的收集、整理与描述练习题2020-2021学年吉林省部分地区七年级下学期人教版数学期末试题选编(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 619.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 19:55:28 | ||
图片预览



文档简介
第十章:数据的收集、整理与描述练习题
一、单选题
1.(2021·吉林敦化·七年级期末)下列选项中,显示部分在总体中所占百分比的统计图是( )
A.扇形统计图 B.条形统计图 C.折线统计图 D.直方图
2.(2021·吉林·舒兰市教师进修学校七年级期末)下列调查中,适合用全面调查方式的是( )
A.了解某校七年级(1)班学生期中数学考试的成绩
B.了解一批签字笔的使用寿命
C.了解市场上酸奶的质量情况
D.了解某条河流的水质情况
3.(2021·吉林铁西·七年级期末)下列调查:
①了解某批种子的发芽率 ②了解某班学生对“社会主义核心价值观”的知晓率
③了解某地区地下水水质 ④了解七年级(1)班学生参加“开放性科学实践活动”完成次数
适合采取全面调查的是( )
A.①③ B.②④ C.①② D.③④
4.(2021·吉林乾安·七年级期末)下列调查:①调查一批灯泡的寿命;②调查某城市居民家庭收入情况;③调查某班学生的视力情况;④调查某种药品的药效.其中适合抽样调查的是()
A.①②③ B.①②④ C.②③④ D.①③④
5.(2021·吉林靖宇·七年级期末)为了解七年级1000名学生的身高情况,从中抽取了300名学生的身高进行统计.这300名学生的身高是( )
A.总体的一个样本 B.个体 C.总体 D.样本容量
6.(2021·吉林前郭尔罗斯·七年级期末)“众志成城,万众一心!”在全国人民共同努力下,新冠肺炎疫情基本可控.为了解校园解封后刚复学时学生的心理健康状况,某中学从该校2000名同学中随机抽取500名同学进行问卷调查,本次调查的样本容量是( )
A.500 B.500名学生的心里健康状况
C.2000 D.2000名学生心里健康状况
7.(2021·吉林永吉·七年级期末)下列调查:①了解全班同学每周体育锻炼的时间;②调查市场上某种食品的色素含量是否符合国家标准;③鞋厂检测生产的鞋底能承受的弯折次数;④了解全班同学的数学学科期末考试成绩.其中适合用抽样调查的是( )
A.①② B.②③ C.③④ D.①④
8.(2021·吉林大安·七年级期末)下列调查中,适合用全面调查方式的是( )
A.了解某校七年级学生期末数学考试的成绩 B.了解一批签字笔的使用寿命
C.了解市场上酸奶的质量情况 D.了解春节联欢晚会的收视率
9.(2021·吉林船营·七年级期末)下列调查中,适宜采用全面调查(普查)方式的是( )
A.对某品牌服装质量的调查 B.对我市九年级学生视力现状的调查
C.对某品牌烟花爆竹燃放安全的调查 D.对一枚运载火箭各零部件的检查
10.(2021·吉林靖宇·七年级期末)下面调查中,最适合采用全面调查的是( )
A.对全国中学生视力状况的调查 B.了解吉林省七年级学生身高情况
C.调查人们保护海洋的意识 D.对“玉兔二号”月球车零部件的调查
11.(2021·吉林·珲春市教师进修学校七年级期末)一组数据的最大值为105,最小值为23,若确定组距为9,则分成的组数为( )
A.11 B.10 C.9 D.8
二、填空题
12.(2021·吉林敦化·七年级期末)妈妈煮一道菜时,为了了解菜的咸淡是否适合,于是取了一点品尝,这属于___(填“全面调查”或“抽样调查”).
13.(2021·吉林双辽·七年级期末)在2020年年末我国完成了农村贫困人口全部脱贫.为了统计农村贫困人口的数量,国家统计局采取的调查方式是__(填“普查”或“抽样调查”).
14.(2021·吉林船营·七年级期末)在一个样本中,40个数据分别落在5个小组内,第1,2,3,5小组的频数分别是2,8,15,5,则第4小组的频数是__________.
15.(2021·吉林靖宇·七年级期末)在数据,,,,,,,,,,,,,,中,范围在(包括前边的数,不包括后边的数)这一组的频数是________.
16.(2021·吉林靖宇·七年级期末)如图,小强同学统计了他家5月份的长途电话明细清单,按通话时间画出直方图,观察直方图,通话时间不超过5的次数是________次.
17.(2021·吉林铁西·七年级期末)在某次数据分析中,该组数据最小值是最大值是若以为组距,则可分____________组.
18.(2021·吉林江源·七年级期末)在频数分布直方图中,各个小组的频数比为,则对应的小长方形的高的比为___________.
三、解答题
19.(2021·吉林铁西·七年级期末)为弘扬中华传统文化,某校开展“双剧进课堂”的活动,该校童威随机抽取部分学生,按四个类别:表示“很喜欢”,表示“喜欢”,表示“一般”,表示“不喜欢”,调查他们对汉剧的喜爱情况,将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题:
(1)这次共抽取_________名学生进行统计调查,扇形统计图中,类所对应的扇形圆心角的大小为__________
(2)将条形统计图补充完整
(3)该校共有1500名学生,估计该校表示“喜欢”的类的学生大约有多少人?
各类学生人数条形统计图各类学生人数扇形统计图
20.(2021·吉林大安·七年级期末)“世界读书日”前夕,某校开展了“读书助我成长”的阅读活动.为了了解该校学生在此次活动中课外阅读书籍的数量情况,随机抽取了部分学生进行调查,将收集到的数据进行整理,绘制出两幅不完整的统计图,请根据统计图信息解决下列问题:
(1)求本次调查中共抽取的学生人数;
(2)补全条形统计图;
(3)在扇形统计图中,阅读本书籍的人数所在扇形的圆心角度数是 ;
(4)若该校有名学生,估计该校在这次活动中阅读书籍的数量不低于本的学生有多少人?
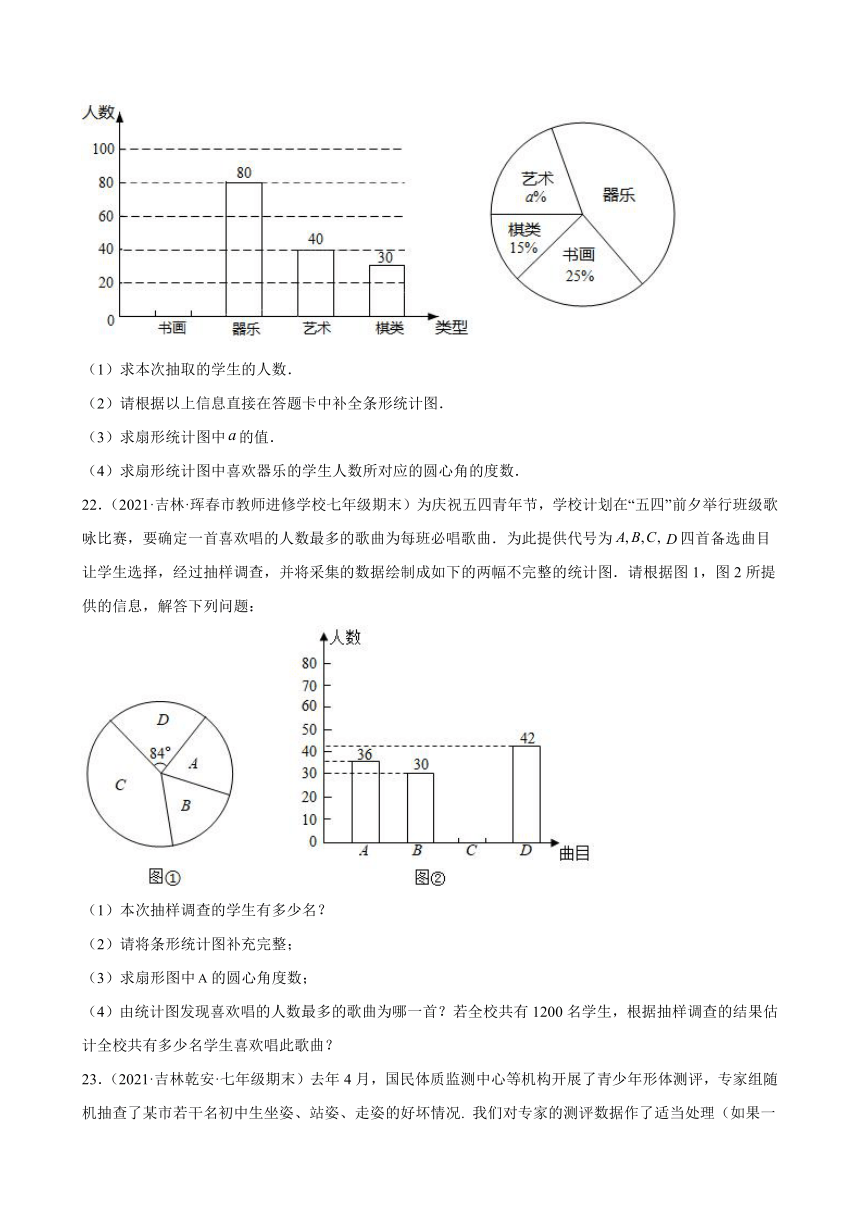
21.(2021·吉林·长春市绿园区教师进修学校七年级期末)小明想了解本校九年级学生对“书画、器乐、艺术、棋类”四项“校本课程”的喜欢情况,随机抽取了部分学生进行问卷调查(每名学生只选择一项),将调查结果整理并绘制成如图所示不完整的统计图.请结合统计图解答下列问题:
(1)求本次抽取的学生的人数.
(2)请根据以上信息直接在答题卡中补全条形统计图.
(3)求扇形统计图中的值.
(4)求扇形统计图中喜欢器乐的学生人数所对应的圆心角的度数.
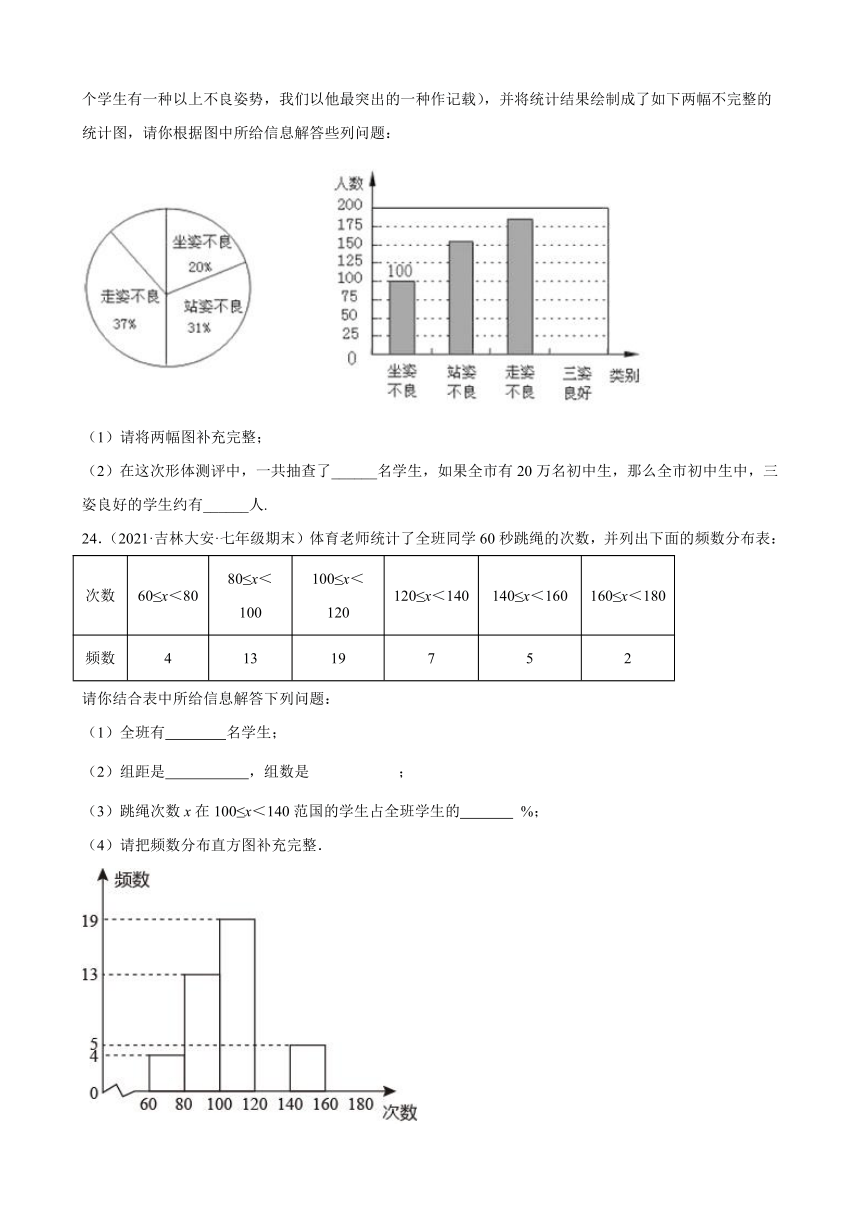
22.(2021·吉林·珲春市教师进修学校七年级期末)为庆祝五四青年节,学校计划在“五四”前夕举行班级歌咏比赛,要确定一首喜欢唱的人数最多的歌曲为每班必唱歌曲.为此提供代号为四首备选曲目让学生选择,经过抽样调查,并将采集的数据绘制成如下的两幅不完整的统计图.请根据图1,图2所提供的信息,解答下列问题:
(1)本次抽样调查的学生有多少名?
(2)请将条形统计图补充完整;
(3)求扇形图中的圆心角度数;
(4)由统计图发现喜欢唱的人数最多的歌曲为哪一首?若全校共有1200名学生,根据抽样调查的结果估计全校共有多少名学生喜欢唱此歌曲?
23.(2021·吉林乾安·七年级期末)去年4月,国民体质监测中心等机构开展了青少年形体测评,专家组随机抽查了某市若干名初中生坐姿、站姿、走姿的好坏情况. 我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制成了如下两幅不完整的统计图,请你根据图中所给信息解答些列问题:
(1)请将两幅图补充完整;
(2)在这次形体测评中,一共抽查了______名学生,如果全市有20万名初中生,那么全市初中生中,三姿良好的学生约有______人.
24.(2021·吉林大安·七年级期末)体育老师统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数 60≤x<80 80≤x<100 100≤x<120 120≤x<140 140≤x<160 160≤x<180
频数 4 13 19 7 5 2
请你结合表中所给信息解答下列问题:
(1)全班有 名学生;
(2)组距是 ,组数是 ;
(3)跳绳次数x在100≤x<140范国的学生占全班学生的 %;
(4)请把频数分布直方图补充完整.
25.(2021·吉林敦化·七年级期末)某校团委随机抽取了名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查,问卷中的家庭活动方式包括:
A.在家里聚餐; B.去影院看电影; C.到公园游玩; D.进行其他活动.
每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式,该校团委收回全部调查问卷后,将收集到的数据整理并绘制成如下的统计图.根据统计图提供的信息,解答下列问题:
名学生喜欢的家庭活动方式的人数条形统计图
(1)请直接写出的值;______
(2)四种方式中最受学生喜欢的方式为______(用,,,作答);选择该种方式的学生人数占被调查的学生人数的百分比为______;
(3)根据统计结果,估计该校1200名学生中喜欢方式的学生比喜欢方式的学生多的人数.
26.(2021·吉林双辽·七年级期末)某校组织全校学生进行“创文明城市知识竞赛”,成绩记为A、B、C、D、E共5个等级,为了解本次竞赛的成绩(等级)情况,现从中随机抽取部分学生的成绩(等级),统计整理并制作了如下的统计图,请根据统计图回答下列问题:
(1)这次抽样调查的样本容量为 ,扇形统计图中C级所占圆心角为 .
(2)补全条形统计图
(3)如果该校共有2000名学生,测试成绩(等级)为A、B级的定为优秀,请估计该校达到优秀的学生有多少名.
27.(2021·吉林前郭尔罗斯·七年级期末)为了解某市2021年初中毕业生的实验考查成绩等级的分布情况,随机抽取了该市若干名学生的实验考查成绩进行统计分析,并根据抽取的成绩绘制了如下统计表和统计图:
成绩等级 A B C D
人数 60 x 30 10
百分比 30% 50% 15% y
请根据以上统计表和统计图提供的信息,解答下列问题:
(1)表中x、y所表示的数分别为:x= ,y= ;
(2)本次抽查的学生有 名;
(3)请补全条形统计图;
(4)根据抽样调查结果,请你估计2021年该县60000名初中毕业生实验考察成绩为D等级的学生人数.
28.(2021·吉林伊通·七年级期末)“某学校为了了解学生的学习兴趣,进行了一次抽样调查.学习兴趣情况分为三个层次,A层次:很感兴趣,B层次:较感兴趣,C层次:不感兴趣,将调查结果绘制成了图①和图②的统计图(不完整).请你根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了__________名学生;
(2)将图①、②补充完整;
(3)图②中C层次所在扇形的圆心角的度数是_________度;
(4)根据抽样调查的结果,请你估计该校1200名学生中大约有多少名学生对学习感兴趣.
29.(2021·吉林永吉·七年级期末)某市教育行政部门为了了解七年级学生每学期参加公益活动的情况,抽样调查了某中学学生一个学期参加公益活动的天数,并用得到的数据绘制了如图所示两幅不完整的统计图.
(1)扇形统计图中a的值是 ,该校七年级学生共有 人;
(2)在该次抽样调查中,参加活动时间为5天的学生共有 人,并补全条形统计图;
(3)如果该市七年级学生共有20000人,估计这20000人中,参加公益活动时间不少于4天的学生有多少人?
30.(2021·吉林船营·七年级期末)随着信息技术的迅猛发展,人们购物的支付方式更加多样、便捷,某校七年级数学兴趣小组就此进行了抽样调查,调查结果显示,支付方式有:A微信;B支付宝;C现金;D其他.该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查购买者的人数是 ;
(2)请补全两幅统计图;
(3)若该超市这一周内大约有4000名购买者,请你估计使用C和D两种支付方式的购买者大约共有多少名?
31.(2021·吉林靖宇·七年级期末)在“全国安全教育日”来临之际,我县某学校举行了安全知识竞赛,学校随机抽取了部分参赛学生的成绩进行整理.根据成绩绘制成不完整的频数分布表和频数分布直方(每组包含最小值,不包含最大值):
成绩 频数 百分比
60---70 15
70---80 20 40%
80---90 20%
90---100 5 10%
请根据上述统计图表信息,解答下列问题:
(1)共抽取了 名学生进行调查, , .
(2)补全频数分布直方图.
(3)若全校有2000名学生,成绩80分及以上者为“优秀”,根据抽样调查结果,估计该校学生得“优秀”等次的学生有 人?
32.(2021·吉林·舒兰市教师进修学校七年级期末)某地区为了了解2021年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.普通高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图.
请据表中信息完成下列问题:
(1)该地区共调查了______名九年级学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该地区2021年初中毕业生共有3600人,请估计该地区2021年初中毕业生中读普通高中的学生人数.
试卷第1页,共3页
参考答案:
1.A
【详解】
根据统计图的特点进行分析可得:扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目.
故在进行数据描述时,要显示部分在总体中所占的百分比,应采用扇形统计图;
故选A.
2.A
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】
解:了解某校七年级(1)班学生期中数学考试的成绩,适合用全面调查方式;
了解一批签字笔的使用寿命适合用抽样调查方式;
了解市场上酸奶的质量情况适合用抽样调查方式;
了解某条河流的水质情况适合用抽样调查方式;
故选A.
【点睛】
本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
3.B
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.
【详解】
①了解某批种子的发芽率适合采取抽样 调查;
②了解某班学生对“社会主义核心价值观”的知晓率适合采取全面调查;
③了解某地区地下水水质适合采取抽样调查;
④了解七年级(1)班学生参加“开放性科学实践活动”完成次数适合采取全面调查;
故选:B.
【点睛】
本题考查的是抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.B
【分析】
调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,全面调查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择全面调查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,全面调查就受到限制,这时就应选择抽样调查;
【详解】
①调查一批灯泡的寿命具有一定的破坏性,故可使用抽样调查的方式;
②调查某城市居民家庭收入情况,调查的范围较大,故可使用抽样调查的方式;
③调查某班学生的视力情况,调查的范围较小,故可使用全面调查的方式;
④调查某种药品的药效具有一定的破坏性,故可使用抽样调查的方式。
所以适合抽样调查的是①②④;
故选:B.
【点睛】
本题主要考查全面调查与抽样调查,准确区分什么情况适合全面调查什么情况适合抽样调查是求解本题的关键.
5.A
【分析】
首先找出考查的对象,从而找出总体、个体,再根据被收集数据的这一部分对象找出样本.
【详解】
300名学生的身高情况是样本.
【点睛】
本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
6.A
【分析】
根据样本容量是指样本中个体的数目,可得答案.
【详解】
解:为了解校园解封后刚复学时学生的心理健康状况,某中学从该校2000名同学中随机抽取500名同学进行问卷调查,本次调查的样本容量是500.
故选:A.
【点睛】
本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
7.B
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】
解:①了解全班同学每周体育锻炼的时间,适合全面调查;
②调查市场上某种食品的色素含量是否符合国家标准,适合抽样调查;
③鞋厂检测生产的鞋底能承受的弯折次数,适合抽样调查;
④了解全班同学的数学学科期末考试成绩,适合全面调查.
所以适合用抽样调查的是②③.
故选:B.
【点睛】
本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
8.A
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,根据以上逐项分析可知.
【详解】
A.了解某校七年级学生期末数学考试的成绩,人员不多,适合普查,故A符合题意;
B.了解一批签字笔的使用寿命,调查范围广,调查具有破坏性,适合抽样调查,故B不符合题意;
C.了解市场上酸奶的质量情况,调查范围广,调查具有破坏性,适合抽样调查,故C不符合题意;
D.了解春节联欢晚会的收视率,调查范围广,适合抽样调查,故D不符合题意.
故选A.
【点睛】
本题考查的是全面调查与抽样调查,在调查实际生活中的相关问题时,要灵活处理,既要考虑问题本身的需要,又要考虑实现的可能性和所付出代价的大小.理解全面调查与抽样调查的适用范围是解题的关键.
9.D
【分析】
根据普查和抽查的特点逐项排查即可.
【详解】
解:A. ∵对某品牌服装质量的调查的工作量比较大,∴不适合全面调查;
B. ∵对我市九年级学生视力现状的调查的工作量比较大,∴不适合全面调查;
C. ∵对某品牌烟花爆竹燃放安全的调查具有破坏性,∴不适合全面调查;
D. ∵对一枚运载火箭各零部件的检查的工作非常重要,∴适合全面调查.
故选D.
【点睛】
本题主要考查了抽样调查和全面调查,由普查得到的调查结果比较准确,但所费人力、物力和时间较多甚至具有破坏性,而抽样调查得到的调查结果比较近似.
10.D
【分析】
根据普查(全面调查)得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.
【详解】
解:A.对全国中学生视力状况的调查,适合抽样调查,故本选项不合题意;
B.了解吉林省七年级学生身高情况,适合抽样调查,故本选项不合题意;
C.调查人们保护海洋的意识,适合抽样调查,故本选项不合题意;
D.对“玉兔二号”月球车零部件的调查,适合普查,故本选项符合题意.
故选:D.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
11.B
【分析】
极差除以组距,大于或等于该值的最小整数即为组数.
【详解】
解:,
分10组.
故选:B.
【点睛】
本题考查了组距的划分,一般分为组最科学.
12.抽样调查
【分析】
根据普查和抽样调查的定义,显然此题属于抽样调查.
【详解】
妈妈煮一道菜时,为了了解菜的咸淡是否适合,于是妈妈取了一点品尝,这属于抽样调查.
故答案为抽样调查.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查;对于精确度要求高的调查,事关重大的调查往往选用普查.
13.普查
【分析】
为了得到全面、可靠的信息,宜采用普查
【详解】
解:为了得到较为全面、可靠的信息,
所以国家统计局采取的调查方式是普查,
故答案为:普查.
【点睛】
本题考查了调查的方式,全面理解调查的方式的意义是解题的关键.
14.10
【分析】
根据各频数的和等于样本容量,可得第4组数据的频数.
【详解】
解:∵40个数据分别落在5个小组内,第1,2,3,5小组的频数分别是2,8,15,5
∴第4小组的频数=40﹣(2+8+15+5)
=40﹣30
=10.
∴第4组数据的频数为10.
故答案为:10.
【点睛】
本题主要考查了频数的定义,关键是熟练掌握频数即样本数据出现的次数.
15.6
【分析】
根据频数的定义:每个对象出现的次数求解即可.
【详解】
解:由题意知:范围在25~27这一组的频数是6,
故答案为:6.
【点睛】
本题考查了频数的定义,属于基础问题.
16.30
【分析】
根据频数分布直方图所反映的数量信息可得答案.
【详解】
解:由频数分布直方图可知,
通话时间不超过5min的次数为30次,
故答案为:30.
【点睛】
本题考查频数分布直方图,从频数分布直方图中获取信息是解决问题的关键.
17.6
【分析】
根据组数=(最大值-最小值) ÷组距计算即可,注意进一法的应用.
【详解】
解:(172-149)÷4=5(组)……3
5+1=6(组)
∴若以为组距,则可分6组
故答案为:6.
【点睛】
本题考查的是组数的计算,属于基础题,掌握组数=(最大值-最小值) ÷组距和进一法是解决此题的关键.
18.
【分析】
根据在一个调查过程中,将所有数据分成四组,各个小组的频数比为3:5:6:2,可以求得画频数分布直方图时对应的小长方形的高的比,本题得以解决.
【详解】
解:∵在一个调查过程中,将所有数据分成四组,
各个小组的频数比为3:5:6:2,
∴画频数分布直方图时对应的小长方形的高的比为3:5:6:2,
故答案为:3:5:6:2.
【点睛】
本题考查频数分布直方图,解题的关键是明确频数分布直方图的画法.
19.(1)50:72°.(1)见解析;(3)690人.
【分析】
(1)根据C类学生的人数以及所占的比例可求得抽取的学生数,再用360度乘以D类学生所占的比例即可求得答案;
(2)先求出A类的学生数,然后补全统计图即可;
(3)用1500乘以B类学生所占的比例即可得.
【详解】
(1)这次共抽取了12÷24%=50名学生进行统计调查,
类所对应的扇形圆心角的大小为360°×=72°,
故答案为50,72°;
(2)A类学生数:50-23-12-10=5,
补全统计图如图所示:
(3)(人),
答:估计该校表示“喜欢”的类的学生大约有690人.
【点睛】
本题考查了条形统计图、扇形统计图,用样本估计总体,弄清题意,读懂统计图,从中找到必要的信息是解题的关键.
20.(1)50(2)见解析(3)(4)600
【分析】
(1)由1本的人数及其所占百分比可得答案;
(2)求出2本和3本的人数即可补全条形图;
(3)用360°乘以2本人数所占比例;
(4)利用样本估计总体思想求解可得.
【详解】
(1)本次调查中共抽取的学生人数为(人);
(2)本人数为(人),
则本人数为(人),
补全图形如下:
(3)在扇形统计图中,阅读本书籍的人数所在扇形的圆心角度数是,
故答案为 ;
(4)估计该校在这次活动中阅读书籍的数量不低于本的学生有(人).
【点睛】
此题考查条形统计图,扇形统计图,用样本估算总体,解题关键在于看懂图中数据
21.(1)200人;(2)图见解析;(3)20;(4).
【分析】
(1)根据喜欢棋类的学生的条形统计图和扇形统计图信息即可得;
(2)先根据(1)的结果求出喜欢书画的学生人数,再补全条形统计图即可得;
(3)利用喜欢艺术学生的人数除以调查的总人数即可得;
(4)利用喜欢器乐的学生人数所占百分比乘以即可得.
【详解】
解:(1)(人),
答:本次抽取的学生有200人;
(2)喜欢书画的学生人数为(人),
由此补全条形统计图如下:
(3),
则;
(4),
答:喜欢器乐的学生人数所对应圆心角的度数为.
【点睛】
本题考查了条形统计图和扇形统计图的信息关联、画条形统计图等知识点,熟练掌握统计调查的相关知识是解题关键.
22.(1)本次抽样调查的学生有180人;(2)见解析;(3)72°;(4)由统计图可知喜欢唱的人数最多的歌曲是C,估计全校共有480人喜欢唱此歌曲.
【分析】
(1)用曲目D的人数除以其占比即可得到答案;
(2)根据(1)所求,先算出曲目C的人数,然后补全统计图即可;
(3)用360度乘以曲目A的人数占比即可得到答案;
(4)根据统计图可知喜欢曲目C的人数最多,然后用全校人数乘以样本中曲目C的占比即可得到答案.
【详解】
解:(1)由题意得:总人数人,
答:本次抽样调查的学生有180人;
(2)由(1)得喜欢曲目C的人数人,
∴补全条形统计图如下所示:
(3)由题意得扇形图中A的圆心角度数;
(4)由统计图可知喜欢唱的人数最多的歌曲是C,估计全校共有人,
答:由统计图可知喜欢唱的人数最多的歌曲是C,估计全校共有480人喜欢唱此歌曲.
【点睛】
本题主要考查了扇形统计图与条形统计图信息相关联,用样本估计总体,补全统计图,求扇形圆心角度数等等,读懂统计图是解题的关键.
23.(1)补全统计图如图;见解析;(2)抽查的学生人数为500人,三姿良好的学生约有24000人.
【分析】
(1)根据各部分所占的百分比的和等于1求出三姿良好所占的百分比,再根据坐姿不良所占的百分比与人数列式求解即可得到三姿良好的人数,然后补全统计图即可;
(2)用坐姿不良的人数除以所占的百分比计算即可求出抽查的人数,再用全市初中生总数乘以三姿良好的学生所占的百分比计算即可得解.
【详解】
(1)三姿良好所占的百分比为:,
三姿良好的人数为:人,
补全统计图如图;
(2)抽查的学生人数为:100÷20%=500人,
三姿良好的学生约有:人,
故答案为500,24000.
【点睛】
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
24.(1)50;(2)20,6;(3)52;(4)见解析
【分析】
(1)依据频数分布表的数据进行计算即可;
(2)依据频数分布表的数据进行判断即可;
(3)依据频数分布表的数据进行计算即可;
(4)依据频数分布表的数据,画出频数分布直方图即可;
【详解】
解:(1)全班学生人数为:(人;
(2)组距是20,组数是6;
(3)跳绳次数在范围的学生占全班学生的百分比为,
故答案是:52;
(4)如图所示:
【点睛】
本题主要考查了频数分布直方图,解题的关键是频率分布表列出的是在各个不同区间内取值的频率,频率分布直方图是用小长方形面积的大小来表示在各个区间内取值的频率.
25.(1)200;(2)C,35%;(3)180名
【分析】
(1)根据条形图,把A,B,C,D的人数加起来,即可解答;
(2)C的学生人数最多,即为四种方式中最受学生喜欢的方式;用C的人数÷总人数,即可得到百分比;
(3)用喜欢C方式的学生人数、喜欢B方式的学生的人数,作差即可解答.
【详解】
解:(1)n=30+40+70+60=200,
故填:200;
(2)∵C的学生人数最多,
∴四种方式中最受学生喜欢的方式为C,
×100%=35%,
故填:C,35%;
(3)(名)
答:该校1200名学生中喜欢C方式的学生比喜欢B方式的学生多180名.
【点睛】
本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.
26.(1)50,36°;(2)见解析;(3)1240
【分析】
(1)根据“B等级”的频数和频率,即可求出样本容量,求出“C等级”所占的百分比,即可求出相应的圆心角的度数;
(2)求出“A等级”的频数即可补全条形统计图;
(3)求出“A等级、B等级”所占整体的百分比即可.
【详解】
解:(1)10÷20%=50(人),
360°×=36°,
故答案为:50,36°;
(2)50-10-5-8-6=21(人),补全条形统计图如图所示:
(3)2000×=1240(名),
答:该校达到优秀的学生有1240名.
【点睛】
本题考查了扇形统计图、条形统计图,解题的关键是理解两个统计图中数量之间的关系.
27.(1)100,5%;(2)200;(3)补全统计图见解析;(4)估计2021年该县60000名初中毕业生实验考察成绩为D等级的学生人数有3000名.
【分析】
(1)先根据成绩是A的人数和百分比求出总人数,然后即可求出x、y的值;
(2)根据(1)中计算的结果求解即可;
(3)根据(1)中计算的结果补全统计图即可;
(4)根据(1)中求得的D等级的学生占比求解即可.
【详解】
解:(1)抽取的总人数是:60÷30%=200(名),
则x=200×50%=100(名),y=×100%=5%;
故答案为:100,5%;
(2)根据(1)可得,本次抽查的学生有200名.
故答案为:200;
(3)根据(1)和统计图给出的数据补全统计图如下:
(4)60000×5%=3000(名),
答:估计2021年该县60000名初中毕业生实验考察成绩为D等级的学生人数有3000名.
【点睛】
本题主要考查了用样本估计总体,条形统计图,频数与频率分布表,解题的关键在于能够准确读懂题意进行求解.
28.(1)200;(2)见解析;(3)54;(4)1020
【分析】
(1)由A层次的人数所占比例为25%,C层次人数为50,得调查总人数为50÷25%=200;
(2)用总人数减去A、B层次的人数即可求得C层次的人数,从而补全统计图;
(3)直接利用360°×C层次的人数占比即可;
(4)由样本中A层次和B层次所占比例为(25%+60%),所以可以估计对学习感兴趣的人数.
【详解】
(1)由图①知A层次的人数是50;由图②知A层次所占的百分比是25%;则此次抽样调查中,共调查的总人数=,
故答案为:200;
(2)C层次的人数为:200-120-50=30(人);
如图:
(3)C层次所在扇形的圆心角的度数是:360×15%=54°,
故答案为:54°;
(4)根据题意得:(25%+60%)×1200=1020(人)
答:估计该校1200名学生中大约有1020名学生对学习感兴趣.
【点睛】
本题主要考查了条形统计图与扇形统计图,用样本估计总体,解题的关键在于能够熟练掌握相关知识进行求解.
29.(1)25,200;(2)50,补全条形统计图详见解答;(3)15000
【分析】
(1)根据“频率之和等于1”可求出5天的所占的百分比,确定a的值,“6天”的频数是30人,占调查人数的15%,根据频率=频数÷总数可求出调查人数;
(2)求出“5天”的人数即可补全条形统计图;
(3)求出样本中“不少于4天”的所占的百分比,即可估计总体的百分比,进而求出相应的人数.
【详解】
解:(1)1﹣10%﹣15%﹣30%﹣15%﹣5%=25%,即a=25,
从两个统计图中可知,“6天”的频数是30人,占调查人数的15%,
所以调查人数为30÷15%=200(人),
故答案为:25,200;
(2)阅读“5天”的人数=200×25%=50(人),
阅读“7天”的人数=200×5%=10(人)
故答案为:50,补全条形统计图如下:
(3)样本中“不少于4天”的百分比
∴这20000人中,参加公益活动时间不少于4天的学生约有20000×75%=15000(人),
答:估计这20000人中,参加公益活动时间不少于4天的学生约有15000人.
【点睛】
本题主要考查了条形统计图与扇形统计图信息相关联,用样本估计总体,解题的关键在于能够准确从统计图中获取信息求解.
30.(1)200;(2)见解析;(3)使用C和D两种支付方式的购买者大约共有1680人
【分析】
(1)根据B的数量和所占的百分比可以求得本次调查的购买者的人数;
(2)根据统计图中的数据可以求得选择A和D的人数,从而可以将统计图补充完整;
(3)根据(2)中的数据可以计算出使用C和D两种支付方式的占比,然后估计总体的使用两种制服方式的人数即可得到答案.
【详解】
解:(1)由统计图可知B种支付方式的人数为56人,占比为28%
∴本次调查的购买者人数=56÷28%=200(人)
(2)由(1)得本次调查的人数为200人,而D种支付方式的占比为20%
∴D种支付方式的人数=200×20%=40(人)
∴A种支付方式的人数=200-56-44-40=60(人)
∴A种支付方式的占比=60÷200=30%
∴C种支付方式的占比=44÷200=22%
∴补全统计图如图所示:
(3)由(2)得C和D种支付方式的占比分别为22%,20%
∴超市一周使用C和D两种支付方式的购买者=(22%+20%)×4000=1680(人)
答:使用C和D两种支付方式的购买者大约共有1680人.
【点睛】
本题考查了扇形统计图、条形统计图、用样本估计总体,解题的关键是明确题意,利用数形结合的思想解答.
31.(1)50,30%,10;(2)见解析;(3)600
【分析】
(1)成绩在“70~80”的人数为20人,占调查人数的40%,根据频率=频数÷总数可求出调查人数,进而求出m、n的值;
(2)根据各组频数即可补全频数分布直方图;
(3)求出样本中,“优秀”所占的百分比,即可估计总体中“优秀”所占的百分比,进而求出相应的人数.
【详解】
解:调查人数为:20÷40%=50(人),
m=15÷50=0.3=30%,
n=50×20%=10(人),
故答案为:50,30%,10;
(2)补全频数分布直方图如下:
(3)2000×(20%+10%)=600(人),
故答案为:600.
【点睛】
本题考查频数分布直方图,频数分布表,掌握频率=频数÷总数是正确解答的关键.
32.(1)200;(2)见解析;(3)1980
【分析】
(1)根据统计图由A的人数和百分比可以得到本次调查的九年级学生数;
(2)根据题目中的数据可以得到统计图中未知的数据,从而可以解答本题;
(3)根据统计图中的数据可以估计该地区今年初中毕业生中读普通高中的学生人数.
【详解】
解:(1)该地区调查的九年级学生人数为110÷55%=200(人),
故答案为:200;
(2)B类别人数为200×35%=70(人),
C类别所占百分比为×100%=8%,
补全图形如下:
(3)3600×55%=1980(人),
答:估计该地区今年初中毕业生中读普通高中的学生人数约有1980人.
【点睛】
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
答案第1页,共2页
一、单选题
1.(2021·吉林敦化·七年级期末)下列选项中,显示部分在总体中所占百分比的统计图是( )
A.扇形统计图 B.条形统计图 C.折线统计图 D.直方图
2.(2021·吉林·舒兰市教师进修学校七年级期末)下列调查中,适合用全面调查方式的是( )
A.了解某校七年级(1)班学生期中数学考试的成绩
B.了解一批签字笔的使用寿命
C.了解市场上酸奶的质量情况
D.了解某条河流的水质情况
3.(2021·吉林铁西·七年级期末)下列调查:
①了解某批种子的发芽率 ②了解某班学生对“社会主义核心价值观”的知晓率
③了解某地区地下水水质 ④了解七年级(1)班学生参加“开放性科学实践活动”完成次数
适合采取全面调查的是( )
A.①③ B.②④ C.①② D.③④
4.(2021·吉林乾安·七年级期末)下列调查:①调查一批灯泡的寿命;②调查某城市居民家庭收入情况;③调查某班学生的视力情况;④调查某种药品的药效.其中适合抽样调查的是()
A.①②③ B.①②④ C.②③④ D.①③④
5.(2021·吉林靖宇·七年级期末)为了解七年级1000名学生的身高情况,从中抽取了300名学生的身高进行统计.这300名学生的身高是( )
A.总体的一个样本 B.个体 C.总体 D.样本容量
6.(2021·吉林前郭尔罗斯·七年级期末)“众志成城,万众一心!”在全国人民共同努力下,新冠肺炎疫情基本可控.为了解校园解封后刚复学时学生的心理健康状况,某中学从该校2000名同学中随机抽取500名同学进行问卷调查,本次调查的样本容量是( )
A.500 B.500名学生的心里健康状况
C.2000 D.2000名学生心里健康状况
7.(2021·吉林永吉·七年级期末)下列调查:①了解全班同学每周体育锻炼的时间;②调查市场上某种食品的色素含量是否符合国家标准;③鞋厂检测生产的鞋底能承受的弯折次数;④了解全班同学的数学学科期末考试成绩.其中适合用抽样调查的是( )
A.①② B.②③ C.③④ D.①④
8.(2021·吉林大安·七年级期末)下列调查中,适合用全面调查方式的是( )
A.了解某校七年级学生期末数学考试的成绩 B.了解一批签字笔的使用寿命
C.了解市场上酸奶的质量情况 D.了解春节联欢晚会的收视率
9.(2021·吉林船营·七年级期末)下列调查中,适宜采用全面调查(普查)方式的是( )
A.对某品牌服装质量的调查 B.对我市九年级学生视力现状的调查
C.对某品牌烟花爆竹燃放安全的调查 D.对一枚运载火箭各零部件的检查
10.(2021·吉林靖宇·七年级期末)下面调查中,最适合采用全面调查的是( )
A.对全国中学生视力状况的调查 B.了解吉林省七年级学生身高情况
C.调查人们保护海洋的意识 D.对“玉兔二号”月球车零部件的调查
11.(2021·吉林·珲春市教师进修学校七年级期末)一组数据的最大值为105,最小值为23,若确定组距为9,则分成的组数为( )
A.11 B.10 C.9 D.8
二、填空题
12.(2021·吉林敦化·七年级期末)妈妈煮一道菜时,为了了解菜的咸淡是否适合,于是取了一点品尝,这属于___(填“全面调查”或“抽样调查”).
13.(2021·吉林双辽·七年级期末)在2020年年末我国完成了农村贫困人口全部脱贫.为了统计农村贫困人口的数量,国家统计局采取的调查方式是__(填“普查”或“抽样调查”).
14.(2021·吉林船营·七年级期末)在一个样本中,40个数据分别落在5个小组内,第1,2,3,5小组的频数分别是2,8,15,5,则第4小组的频数是__________.
15.(2021·吉林靖宇·七年级期末)在数据,,,,,,,,,,,,,,中,范围在(包括前边的数,不包括后边的数)这一组的频数是________.
16.(2021·吉林靖宇·七年级期末)如图,小强同学统计了他家5月份的长途电话明细清单,按通话时间画出直方图,观察直方图,通话时间不超过5的次数是________次.
17.(2021·吉林铁西·七年级期末)在某次数据分析中,该组数据最小值是最大值是若以为组距,则可分____________组.
18.(2021·吉林江源·七年级期末)在频数分布直方图中,各个小组的频数比为,则对应的小长方形的高的比为___________.
三、解答题
19.(2021·吉林铁西·七年级期末)为弘扬中华传统文化,某校开展“双剧进课堂”的活动,该校童威随机抽取部分学生,按四个类别:表示“很喜欢”,表示“喜欢”,表示“一般”,表示“不喜欢”,调查他们对汉剧的喜爱情况,将结果绘制成如下两幅不完整的统计图,根据图中提供的信息,解决下列问题:
(1)这次共抽取_________名学生进行统计调查,扇形统计图中,类所对应的扇形圆心角的大小为__________
(2)将条形统计图补充完整
(3)该校共有1500名学生,估计该校表示“喜欢”的类的学生大约有多少人?
各类学生人数条形统计图各类学生人数扇形统计图
20.(2021·吉林大安·七年级期末)“世界读书日”前夕,某校开展了“读书助我成长”的阅读活动.为了了解该校学生在此次活动中课外阅读书籍的数量情况,随机抽取了部分学生进行调查,将收集到的数据进行整理,绘制出两幅不完整的统计图,请根据统计图信息解决下列问题:
(1)求本次调查中共抽取的学生人数;
(2)补全条形统计图;
(3)在扇形统计图中,阅读本书籍的人数所在扇形的圆心角度数是 ;
(4)若该校有名学生,估计该校在这次活动中阅读书籍的数量不低于本的学生有多少人?
21.(2021·吉林·长春市绿园区教师进修学校七年级期末)小明想了解本校九年级学生对“书画、器乐、艺术、棋类”四项“校本课程”的喜欢情况,随机抽取了部分学生进行问卷调查(每名学生只选择一项),将调查结果整理并绘制成如图所示不完整的统计图.请结合统计图解答下列问题:
(1)求本次抽取的学生的人数.
(2)请根据以上信息直接在答题卡中补全条形统计图.
(3)求扇形统计图中的值.
(4)求扇形统计图中喜欢器乐的学生人数所对应的圆心角的度数.
22.(2021·吉林·珲春市教师进修学校七年级期末)为庆祝五四青年节,学校计划在“五四”前夕举行班级歌咏比赛,要确定一首喜欢唱的人数最多的歌曲为每班必唱歌曲.为此提供代号为四首备选曲目让学生选择,经过抽样调查,并将采集的数据绘制成如下的两幅不完整的统计图.请根据图1,图2所提供的信息,解答下列问题:
(1)本次抽样调查的学生有多少名?
(2)请将条形统计图补充完整;
(3)求扇形图中的圆心角度数;
(4)由统计图发现喜欢唱的人数最多的歌曲为哪一首?若全校共有1200名学生,根据抽样调查的结果估计全校共有多少名学生喜欢唱此歌曲?
23.(2021·吉林乾安·七年级期末)去年4月,国民体质监测中心等机构开展了青少年形体测评,专家组随机抽查了某市若干名初中生坐姿、站姿、走姿的好坏情况. 我们对专家的测评数据作了适当处理(如果一个学生有一种以上不良姿势,我们以他最突出的一种作记载),并将统计结果绘制成了如下两幅不完整的统计图,请你根据图中所给信息解答些列问题:
(1)请将两幅图补充完整;
(2)在这次形体测评中,一共抽查了______名学生,如果全市有20万名初中生,那么全市初中生中,三姿良好的学生约有______人.
24.(2021·吉林大安·七年级期末)体育老师统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数 60≤x<80 80≤x<100 100≤x<120 120≤x<140 140≤x<160 160≤x<180
频数 4 13 19 7 5 2
请你结合表中所给信息解答下列问题:
(1)全班有 名学生;
(2)组距是 ,组数是 ;
(3)跳绳次数x在100≤x<140范国的学生占全班学生的 %;
(4)请把频数分布直方图补充完整.
25.(2021·吉林敦化·七年级期末)某校团委随机抽取了名本校学生,对“世界家庭日”当天所喜欢的家庭活动方式进行问卷调查,问卷中的家庭活动方式包括:
A.在家里聚餐; B.去影院看电影; C.到公园游玩; D.进行其他活动.
每位学生在问卷调查时都按要求只选择了其中一种喜欢的活动方式,该校团委收回全部调查问卷后,将收集到的数据整理并绘制成如下的统计图.根据统计图提供的信息,解答下列问题:
名学生喜欢的家庭活动方式的人数条形统计图
(1)请直接写出的值;______
(2)四种方式中最受学生喜欢的方式为______(用,,,作答);选择该种方式的学生人数占被调查的学生人数的百分比为______;
(3)根据统计结果,估计该校1200名学生中喜欢方式的学生比喜欢方式的学生多的人数.
26.(2021·吉林双辽·七年级期末)某校组织全校学生进行“创文明城市知识竞赛”,成绩记为A、B、C、D、E共5个等级,为了解本次竞赛的成绩(等级)情况,现从中随机抽取部分学生的成绩(等级),统计整理并制作了如下的统计图,请根据统计图回答下列问题:
(1)这次抽样调查的样本容量为 ,扇形统计图中C级所占圆心角为 .
(2)补全条形统计图
(3)如果该校共有2000名学生,测试成绩(等级)为A、B级的定为优秀,请估计该校达到优秀的学生有多少名.
27.(2021·吉林前郭尔罗斯·七年级期末)为了解某市2021年初中毕业生的实验考查成绩等级的分布情况,随机抽取了该市若干名学生的实验考查成绩进行统计分析,并根据抽取的成绩绘制了如下统计表和统计图:
成绩等级 A B C D
人数 60 x 30 10
百分比 30% 50% 15% y
请根据以上统计表和统计图提供的信息,解答下列问题:
(1)表中x、y所表示的数分别为:x= ,y= ;
(2)本次抽查的学生有 名;
(3)请补全条形统计图;
(4)根据抽样调查结果,请你估计2021年该县60000名初中毕业生实验考察成绩为D等级的学生人数.
28.(2021·吉林伊通·七年级期末)“某学校为了了解学生的学习兴趣,进行了一次抽样调查.学习兴趣情况分为三个层次,A层次:很感兴趣,B层次:较感兴趣,C层次:不感兴趣,将调查结果绘制成了图①和图②的统计图(不完整).请你根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了__________名学生;
(2)将图①、②补充完整;
(3)图②中C层次所在扇形的圆心角的度数是_________度;
(4)根据抽样调查的结果,请你估计该校1200名学生中大约有多少名学生对学习感兴趣.
29.(2021·吉林永吉·七年级期末)某市教育行政部门为了了解七年级学生每学期参加公益活动的情况,抽样调查了某中学学生一个学期参加公益活动的天数,并用得到的数据绘制了如图所示两幅不完整的统计图.
(1)扇形统计图中a的值是 ,该校七年级学生共有 人;
(2)在该次抽样调查中,参加活动时间为5天的学生共有 人,并补全条形统计图;
(3)如果该市七年级学生共有20000人,估计这20000人中,参加公益活动时间不少于4天的学生有多少人?
30.(2021·吉林船营·七年级期末)随着信息技术的迅猛发展,人们购物的支付方式更加多样、便捷,某校七年级数学兴趣小组就此进行了抽样调查,调查结果显示,支付方式有:A微信;B支付宝;C现金;D其他.该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查购买者的人数是 ;
(2)请补全两幅统计图;
(3)若该超市这一周内大约有4000名购买者,请你估计使用C和D两种支付方式的购买者大约共有多少名?
31.(2021·吉林靖宇·七年级期末)在“全国安全教育日”来临之际,我县某学校举行了安全知识竞赛,学校随机抽取了部分参赛学生的成绩进行整理.根据成绩绘制成不完整的频数分布表和频数分布直方(每组包含最小值,不包含最大值):
成绩 频数 百分比
60---70 15
70---80 20 40%
80---90 20%
90---100 5 10%
请根据上述统计图表信息,解答下列问题:
(1)共抽取了 名学生进行调查, , .
(2)补全频数分布直方图.
(3)若全校有2000名学生,成绩80分及以上者为“优秀”,根据抽样调查结果,估计该校学生得“优秀”等次的学生有 人?
32.(2021·吉林·舒兰市教师进修学校七年级期末)某地区为了了解2021年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.普通高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图.
请据表中信息完成下列问题:
(1)该地区共调查了______名九年级学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该地区2021年初中毕业生共有3600人,请估计该地区2021年初中毕业生中读普通高中的学生人数.
试卷第1页,共3页
参考答案:
1.A
【详解】
根据统计图的特点进行分析可得:扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目.
故在进行数据描述时,要显示部分在总体中所占的百分比,应采用扇形统计图;
故选A.
2.A
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】
解:了解某校七年级(1)班学生期中数学考试的成绩,适合用全面调查方式;
了解一批签字笔的使用寿命适合用抽样调查方式;
了解市场上酸奶的质量情况适合用抽样调查方式;
了解某条河流的水质情况适合用抽样调查方式;
故选A.
【点睛】
本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
3.B
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.
【详解】
①了解某批种子的发芽率适合采取抽样 调查;
②了解某班学生对“社会主义核心价值观”的知晓率适合采取全面调查;
③了解某地区地下水水质适合采取抽样调查;
④了解七年级(1)班学生参加“开放性科学实践活动”完成次数适合采取全面调查;
故选:B.
【点睛】
本题考查的是抽样调查和全面调查,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
4.B
【分析】
调查方式的选择需要将普查的局限性和抽样调查的必要性结合起来,具体问题具体分析,全面调查结果准确,所以在要求精确、难度相对不大,实验无破坏性的情况下应选择全面调查方式,当考查的对象很多或考查会给被调查对象带来损伤破坏,以及考查经费和时间都非常有限时,全面调查就受到限制,这时就应选择抽样调查;
【详解】
①调查一批灯泡的寿命具有一定的破坏性,故可使用抽样调查的方式;
②调查某城市居民家庭收入情况,调查的范围较大,故可使用抽样调查的方式;
③调查某班学生的视力情况,调查的范围较小,故可使用全面调查的方式;
④调查某种药品的药效具有一定的破坏性,故可使用抽样调查的方式。
所以适合抽样调查的是①②④;
故选:B.
【点睛】
本题主要考查全面调查与抽样调查,准确区分什么情况适合全面调查什么情况适合抽样调查是求解本题的关键.
5.A
【分析】
首先找出考查的对象,从而找出总体、个体,再根据被收集数据的这一部分对象找出样本.
【详解】
300名学生的身高情况是样本.
【点睛】
本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
6.A
【分析】
根据样本容量是指样本中个体的数目,可得答案.
【详解】
解:为了解校园解封后刚复学时学生的心理健康状况,某中学从该校2000名同学中随机抽取500名同学进行问卷调查,本次调查的样本容量是500.
故选:A.
【点睛】
本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.
7.B
【分析】
根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似解答.
【详解】
解:①了解全班同学每周体育锻炼的时间,适合全面调查;
②调查市场上某种食品的色素含量是否符合国家标准,适合抽样调查;
③鞋厂检测生产的鞋底能承受的弯折次数,适合抽样调查;
④了解全班同学的数学学科期末考试成绩,适合全面调查.
所以适合用抽样调查的是②③.
故选:B.
【点睛】
本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
8.A
【分析】
由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似,根据以上逐项分析可知.
【详解】
A.了解某校七年级学生期末数学考试的成绩,人员不多,适合普查,故A符合题意;
B.了解一批签字笔的使用寿命,调查范围广,调查具有破坏性,适合抽样调查,故B不符合题意;
C.了解市场上酸奶的质量情况,调查范围广,调查具有破坏性,适合抽样调查,故C不符合题意;
D.了解春节联欢晚会的收视率,调查范围广,适合抽样调查,故D不符合题意.
故选A.
【点睛】
本题考查的是全面调查与抽样调查,在调查实际生活中的相关问题时,要灵活处理,既要考虑问题本身的需要,又要考虑实现的可能性和所付出代价的大小.理解全面调查与抽样调查的适用范围是解题的关键.
9.D
【分析】
根据普查和抽查的特点逐项排查即可.
【详解】
解:A. ∵对某品牌服装质量的调查的工作量比较大,∴不适合全面调查;
B. ∵对我市九年级学生视力现状的调查的工作量比较大,∴不适合全面调查;
C. ∵对某品牌烟花爆竹燃放安全的调查具有破坏性,∴不适合全面调查;
D. ∵对一枚运载火箭各零部件的检查的工作非常重要,∴适合全面调查.
故选D.
【点睛】
本题主要考查了抽样调查和全面调查,由普查得到的调查结果比较准确,但所费人力、物力和时间较多甚至具有破坏性,而抽样调查得到的调查结果比较近似.
10.D
【分析】
根据普查(全面调查)得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.
【详解】
解:A.对全国中学生视力状况的调查,适合抽样调查,故本选项不合题意;
B.了解吉林省七年级学生身高情况,适合抽样调查,故本选项不合题意;
C.调查人们保护海洋的意识,适合抽样调查,故本选项不合题意;
D.对“玉兔二号”月球车零部件的调查,适合普查,故本选项符合题意.
故选:D.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
11.B
【分析】
极差除以组距,大于或等于该值的最小整数即为组数.
【详解】
解:,
分10组.
故选:B.
【点睛】
本题考查了组距的划分,一般分为组最科学.
12.抽样调查
【分析】
根据普查和抽样调查的定义,显然此题属于抽样调查.
【详解】
妈妈煮一道菜时,为了了解菜的咸淡是否适合,于是妈妈取了一点品尝,这属于抽样调查.
故答案为抽样调查.
【点睛】
本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大时,应选择抽样调查;对于精确度要求高的调查,事关重大的调查往往选用普查.
13.普查
【分析】
为了得到全面、可靠的信息,宜采用普查
【详解】
解:为了得到较为全面、可靠的信息,
所以国家统计局采取的调查方式是普查,
故答案为:普查.
【点睛】
本题考查了调查的方式,全面理解调查的方式的意义是解题的关键.
14.10
【分析】
根据各频数的和等于样本容量,可得第4组数据的频数.
【详解】
解:∵40个数据分别落在5个小组内,第1,2,3,5小组的频数分别是2,8,15,5
∴第4小组的频数=40﹣(2+8+15+5)
=40﹣30
=10.
∴第4组数据的频数为10.
故答案为:10.
【点睛】
本题主要考查了频数的定义,关键是熟练掌握频数即样本数据出现的次数.
15.6
【分析】
根据频数的定义:每个对象出现的次数求解即可.
【详解】
解:由题意知:范围在25~27这一组的频数是6,
故答案为:6.
【点睛】
本题考查了频数的定义,属于基础问题.
16.30
【分析】
根据频数分布直方图所反映的数量信息可得答案.
【详解】
解:由频数分布直方图可知,
通话时间不超过5min的次数为30次,
故答案为:30.
【点睛】
本题考查频数分布直方图,从频数分布直方图中获取信息是解决问题的关键.
17.6
【分析】
根据组数=(最大值-最小值) ÷组距计算即可,注意进一法的应用.
【详解】
解:(172-149)÷4=5(组)……3
5+1=6(组)
∴若以为组距,则可分6组
故答案为:6.
【点睛】
本题考查的是组数的计算,属于基础题,掌握组数=(最大值-最小值) ÷组距和进一法是解决此题的关键.
18.
【分析】
根据在一个调查过程中,将所有数据分成四组,各个小组的频数比为3:5:6:2,可以求得画频数分布直方图时对应的小长方形的高的比,本题得以解决.
【详解】
解:∵在一个调查过程中,将所有数据分成四组,
各个小组的频数比为3:5:6:2,
∴画频数分布直方图时对应的小长方形的高的比为3:5:6:2,
故答案为:3:5:6:2.
【点睛】
本题考查频数分布直方图,解题的关键是明确频数分布直方图的画法.
19.(1)50:72°.(1)见解析;(3)690人.
【分析】
(1)根据C类学生的人数以及所占的比例可求得抽取的学生数,再用360度乘以D类学生所占的比例即可求得答案;
(2)先求出A类的学生数,然后补全统计图即可;
(3)用1500乘以B类学生所占的比例即可得.
【详解】
(1)这次共抽取了12÷24%=50名学生进行统计调查,
类所对应的扇形圆心角的大小为360°×=72°,
故答案为50,72°;
(2)A类学生数:50-23-12-10=5,
补全统计图如图所示:
(3)(人),
答:估计该校表示“喜欢”的类的学生大约有690人.
【点睛】
本题考查了条形统计图、扇形统计图,用样本估计总体,弄清题意,读懂统计图,从中找到必要的信息是解题的关键.
20.(1)50(2)见解析(3)(4)600
【分析】
(1)由1本的人数及其所占百分比可得答案;
(2)求出2本和3本的人数即可补全条形图;
(3)用360°乘以2本人数所占比例;
(4)利用样本估计总体思想求解可得.
【详解】
(1)本次调查中共抽取的学生人数为(人);
(2)本人数为(人),
则本人数为(人),
补全图形如下:
(3)在扇形统计图中,阅读本书籍的人数所在扇形的圆心角度数是,
故答案为 ;
(4)估计该校在这次活动中阅读书籍的数量不低于本的学生有(人).
【点睛】
此题考查条形统计图,扇形统计图,用样本估算总体,解题关键在于看懂图中数据
21.(1)200人;(2)图见解析;(3)20;(4).
【分析】
(1)根据喜欢棋类的学生的条形统计图和扇形统计图信息即可得;
(2)先根据(1)的结果求出喜欢书画的学生人数,再补全条形统计图即可得;
(3)利用喜欢艺术学生的人数除以调查的总人数即可得;
(4)利用喜欢器乐的学生人数所占百分比乘以即可得.
【详解】
解:(1)(人),
答:本次抽取的学生有200人;
(2)喜欢书画的学生人数为(人),
由此补全条形统计图如下:
(3),
则;
(4),
答:喜欢器乐的学生人数所对应圆心角的度数为.
【点睛】
本题考查了条形统计图和扇形统计图的信息关联、画条形统计图等知识点,熟练掌握统计调查的相关知识是解题关键.
22.(1)本次抽样调查的学生有180人;(2)见解析;(3)72°;(4)由统计图可知喜欢唱的人数最多的歌曲是C,估计全校共有480人喜欢唱此歌曲.
【分析】
(1)用曲目D的人数除以其占比即可得到答案;
(2)根据(1)所求,先算出曲目C的人数,然后补全统计图即可;
(3)用360度乘以曲目A的人数占比即可得到答案;
(4)根据统计图可知喜欢曲目C的人数最多,然后用全校人数乘以样本中曲目C的占比即可得到答案.
【详解】
解:(1)由题意得:总人数人,
答:本次抽样调查的学生有180人;
(2)由(1)得喜欢曲目C的人数人,
∴补全条形统计图如下所示:
(3)由题意得扇形图中A的圆心角度数;
(4)由统计图可知喜欢唱的人数最多的歌曲是C,估计全校共有人,
答:由统计图可知喜欢唱的人数最多的歌曲是C,估计全校共有480人喜欢唱此歌曲.
【点睛】
本题主要考查了扇形统计图与条形统计图信息相关联,用样本估计总体,补全统计图,求扇形圆心角度数等等,读懂统计图是解题的关键.
23.(1)补全统计图如图;见解析;(2)抽查的学生人数为500人,三姿良好的学生约有24000人.
【分析】
(1)根据各部分所占的百分比的和等于1求出三姿良好所占的百分比,再根据坐姿不良所占的百分比与人数列式求解即可得到三姿良好的人数,然后补全统计图即可;
(2)用坐姿不良的人数除以所占的百分比计算即可求出抽查的人数,再用全市初中生总数乘以三姿良好的学生所占的百分比计算即可得解.
【详解】
(1)三姿良好所占的百分比为:,
三姿良好的人数为:人,
补全统计图如图;
(2)抽查的学生人数为:100÷20%=500人,
三姿良好的学生约有:人,
故答案为500,24000.
【点睛】
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
24.(1)50;(2)20,6;(3)52;(4)见解析
【分析】
(1)依据频数分布表的数据进行计算即可;
(2)依据频数分布表的数据进行判断即可;
(3)依据频数分布表的数据进行计算即可;
(4)依据频数分布表的数据,画出频数分布直方图即可;
【详解】
解:(1)全班学生人数为:(人;
(2)组距是20,组数是6;
(3)跳绳次数在范围的学生占全班学生的百分比为,
故答案是:52;
(4)如图所示:
【点睛】
本题主要考查了频数分布直方图,解题的关键是频率分布表列出的是在各个不同区间内取值的频率,频率分布直方图是用小长方形面积的大小来表示在各个区间内取值的频率.
25.(1)200;(2)C,35%;(3)180名
【分析】
(1)根据条形图,把A,B,C,D的人数加起来,即可解答;
(2)C的学生人数最多,即为四种方式中最受学生喜欢的方式;用C的人数÷总人数,即可得到百分比;
(3)用喜欢C方式的学生人数、喜欢B方式的学生的人数,作差即可解答.
【详解】
解:(1)n=30+40+70+60=200,
故填:200;
(2)∵C的学生人数最多,
∴四种方式中最受学生喜欢的方式为C,
×100%=35%,
故填:C,35%;
(3)(名)
答:该校1200名学生中喜欢C方式的学生比喜欢B方式的学生多180名.
【点睛】
本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.
26.(1)50,36°;(2)见解析;(3)1240
【分析】
(1)根据“B等级”的频数和频率,即可求出样本容量,求出“C等级”所占的百分比,即可求出相应的圆心角的度数;
(2)求出“A等级”的频数即可补全条形统计图;
(3)求出“A等级、B等级”所占整体的百分比即可.
【详解】
解:(1)10÷20%=50(人),
360°×=36°,
故答案为:50,36°;
(2)50-10-5-8-6=21(人),补全条形统计图如图所示:
(3)2000×=1240(名),
答:该校达到优秀的学生有1240名.
【点睛】
本题考查了扇形统计图、条形统计图,解题的关键是理解两个统计图中数量之间的关系.
27.(1)100,5%;(2)200;(3)补全统计图见解析;(4)估计2021年该县60000名初中毕业生实验考察成绩为D等级的学生人数有3000名.
【分析】
(1)先根据成绩是A的人数和百分比求出总人数,然后即可求出x、y的值;
(2)根据(1)中计算的结果求解即可;
(3)根据(1)中计算的结果补全统计图即可;
(4)根据(1)中求得的D等级的学生占比求解即可.
【详解】
解:(1)抽取的总人数是:60÷30%=200(名),
则x=200×50%=100(名),y=×100%=5%;
故答案为:100,5%;
(2)根据(1)可得,本次抽查的学生有200名.
故答案为:200;
(3)根据(1)和统计图给出的数据补全统计图如下:
(4)60000×5%=3000(名),
答:估计2021年该县60000名初中毕业生实验考察成绩为D等级的学生人数有3000名.
【点睛】
本题主要考查了用样本估计总体,条形统计图,频数与频率分布表,解题的关键在于能够准确读懂题意进行求解.
28.(1)200;(2)见解析;(3)54;(4)1020
【分析】
(1)由A层次的人数所占比例为25%,C层次人数为50,得调查总人数为50÷25%=200;
(2)用总人数减去A、B层次的人数即可求得C层次的人数,从而补全统计图;
(3)直接利用360°×C层次的人数占比即可;
(4)由样本中A层次和B层次所占比例为(25%+60%),所以可以估计对学习感兴趣的人数.
【详解】
(1)由图①知A层次的人数是50;由图②知A层次所占的百分比是25%;则此次抽样调查中,共调查的总人数=,
故答案为:200;
(2)C层次的人数为:200-120-50=30(人);
如图:
(3)C层次所在扇形的圆心角的度数是:360×15%=54°,
故答案为:54°;
(4)根据题意得:(25%+60%)×1200=1020(人)
答:估计该校1200名学生中大约有1020名学生对学习感兴趣.
【点睛】
本题主要考查了条形统计图与扇形统计图,用样本估计总体,解题的关键在于能够熟练掌握相关知识进行求解.
29.(1)25,200;(2)50,补全条形统计图详见解答;(3)15000
【分析】
(1)根据“频率之和等于1”可求出5天的所占的百分比,确定a的值,“6天”的频数是30人,占调查人数的15%,根据频率=频数÷总数可求出调查人数;
(2)求出“5天”的人数即可补全条形统计图;
(3)求出样本中“不少于4天”的所占的百分比,即可估计总体的百分比,进而求出相应的人数.
【详解】
解:(1)1﹣10%﹣15%﹣30%﹣15%﹣5%=25%,即a=25,
从两个统计图中可知,“6天”的频数是30人,占调查人数的15%,
所以调查人数为30÷15%=200(人),
故答案为:25,200;
(2)阅读“5天”的人数=200×25%=50(人),
阅读“7天”的人数=200×5%=10(人)
故答案为:50,补全条形统计图如下:
(3)样本中“不少于4天”的百分比
∴这20000人中,参加公益活动时间不少于4天的学生约有20000×75%=15000(人),
答:估计这20000人中,参加公益活动时间不少于4天的学生约有15000人.
【点睛】
本题主要考查了条形统计图与扇形统计图信息相关联,用样本估计总体,解题的关键在于能够准确从统计图中获取信息求解.
30.(1)200;(2)见解析;(3)使用C和D两种支付方式的购买者大约共有1680人
【分析】
(1)根据B的数量和所占的百分比可以求得本次调查的购买者的人数;
(2)根据统计图中的数据可以求得选择A和D的人数,从而可以将统计图补充完整;
(3)根据(2)中的数据可以计算出使用C和D两种支付方式的占比,然后估计总体的使用两种制服方式的人数即可得到答案.
【详解】
解:(1)由统计图可知B种支付方式的人数为56人,占比为28%
∴本次调查的购买者人数=56÷28%=200(人)
(2)由(1)得本次调查的人数为200人,而D种支付方式的占比为20%
∴D种支付方式的人数=200×20%=40(人)
∴A种支付方式的人数=200-56-44-40=60(人)
∴A种支付方式的占比=60÷200=30%
∴C种支付方式的占比=44÷200=22%
∴补全统计图如图所示:
(3)由(2)得C和D种支付方式的占比分别为22%,20%
∴超市一周使用C和D两种支付方式的购买者=(22%+20%)×4000=1680(人)
答:使用C和D两种支付方式的购买者大约共有1680人.
【点睛】
本题考查了扇形统计图、条形统计图、用样本估计总体,解题的关键是明确题意,利用数形结合的思想解答.
31.(1)50,30%,10;(2)见解析;(3)600
【分析】
(1)成绩在“70~80”的人数为20人,占调查人数的40%,根据频率=频数÷总数可求出调查人数,进而求出m、n的值;
(2)根据各组频数即可补全频数分布直方图;
(3)求出样本中,“优秀”所占的百分比,即可估计总体中“优秀”所占的百分比,进而求出相应的人数.
【详解】
解:调查人数为:20÷40%=50(人),
m=15÷50=0.3=30%,
n=50×20%=10(人),
故答案为:50,30%,10;
(2)补全频数分布直方图如下:
(3)2000×(20%+10%)=600(人),
故答案为:600.
【点睛】
本题考查频数分布直方图,频数分布表,掌握频率=频数÷总数是正确解答的关键.
32.(1)200;(2)见解析;(3)1980
【分析】
(1)根据统计图由A的人数和百分比可以得到本次调查的九年级学生数;
(2)根据题目中的数据可以得到统计图中未知的数据,从而可以解答本题;
(3)根据统计图中的数据可以估计该地区今年初中毕业生中读普通高中的学生人数.
【详解】
解:(1)该地区调查的九年级学生人数为110÷55%=200(人),
故答案为:200;
(2)B类别人数为200×35%=70(人),
C类别所占百分比为×100%=8%,
补全图形如下:
(3)3600×55%=1980(人),
答:估计该地区今年初中毕业生中读普通高中的学生人数约有1980人.
【点睛】
本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
答案第1页,共2页
