2021-2022学年北师大版九年级数学下册第三章圆单元复习训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第三章圆单元复习训练卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 309.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 23:47:09 | ||
图片预览



文档简介
北师大版九年级数学下册
第三章 圆
单元复习训练卷
一、选择题(共10小题,4*10=40)
1. 已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A.点P在⊙O外
B.点P在⊙O内
C.点P在⊙O上
D.无法确定
2. 已知⊙O的半径为5 cm,圆心O到直线l的距离为5 cm,则直线l与⊙O的位置关系为( )
A.相交 B.相切
C.相离 D.无法确定
3. 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. B.2 C.2 D.8
4. 两圆既不相交又不相切,半径分别为3和5,则两圆的圆心距d的取值范围是( )
A. d>8 B. 0<d≤2
C. 2<d<8 D. 0≤d<2或d>8
5. 如图,直线l与⊙O相交于A,B两点,且与半径OC垂直,垂足为H,已知AB=16cm,sin∠OBH=,则⊙O的半径为( )
A.6cm B.10cm C.12cm D.cm
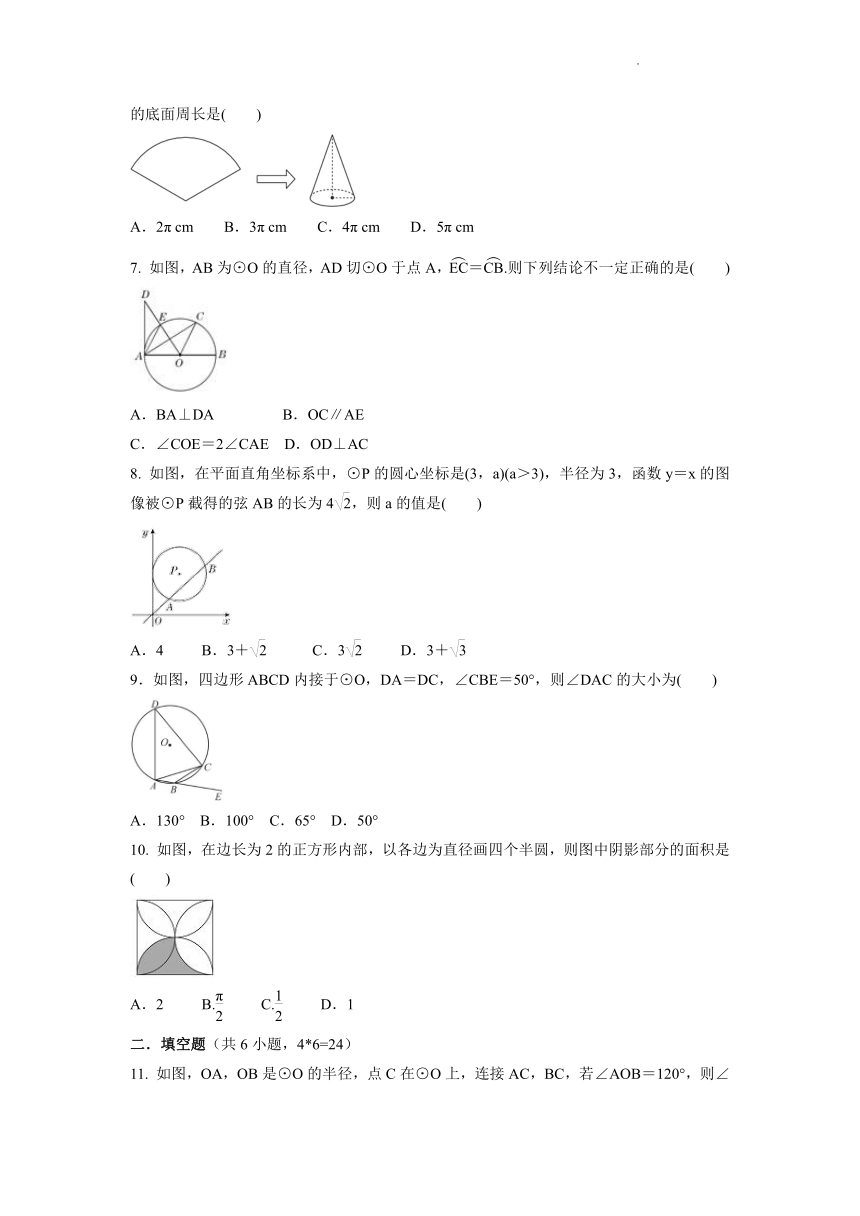
6. 用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(如图),则这个纸帽的底面周长是( )
A.2π cm B.3π cm C.4π cm D.5π cm
7. 如图,AB为⊙O的直径,AD切⊙O于点A,=.则下列结论不一定正确的是( )
A.BA⊥DA B.OC∥AE
C.∠COE=2∠CAE D.OD⊥AC
8. 如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图像被⊙P截得的弦AB的长为4,则a的值是( )
A.4 B.3+ C.3 D.3+
9.如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
A.130° B.100° C.65° D.50°
10. 如图,在边长为2的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是( )
A.2 B. C. D.1
二.填空题(共6小题,4*6=24)
11. 如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若∠AOB=120°,则∠ACB= .
12. 如图,P为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E且分别交PA,PB于点C,D,若PA=4,则△PCD的周长为_______.
13. 如图,已知PA,PB是⊙O的切线,A. B为切点,AC是⊙O的直径,∠P=40°,则∠BAC度数是 ;
14. 如图,一根5 m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊(羊只能在草地上活动),那么小羊在草地上的最大活动区域的面积是________.
15..如图,CD是☉O的直径,点A是半圆上的三等分点,B是的中点,P为直线CD上的一个动点,当CD=6时,AP+BP的最小值为 .
16.如图,直线l与半径为4的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连结PA.设PA=x,PB=y,则x-y的最大值是________.
三.解答题(共5小题, 56分)
17.(6分) 如图,AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC,OC,BC.求证:∠ACO=∠BCD.
18.(8分) 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,以点C为圆心,BC为半径作圆交AB于点D,求AD的长.
19.(8分) 如图,A,B是⊙O上的两点,∠AOB=120°,C是的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至点P,使OA=AP,连接PC,若⊙O的半径R=1,求PC的长.
20.(10分) 如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C,交PB于点D,连接BC,当∠P=30°时:
(1)求弦AC的长;
(2)求证:BC∥PA.
21.(12分) 如图,有一个圆O和两个正六边形T1,T2,T1的六个顶点都在圆周上,T2的六条边都和圆O相切(称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b,圆O的半径为r,求r:a与r:b;
(2)设正六边形T1的面积为S1,正六边形T2的面积为S2,求S1:S2.
22.(12分) 如图,将边长为2的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动.
(1)该正六边形的每一个内角的度数是________,每一个外角的度数为________;
(2)求它的对角线A1A5,A2A4,A1A3的长;
(3)直接写出点A1从图1滚动到图2的位置时,顶点A1所经过的路径长.
参考答案
1-5ABCDB 6-10CDBCD
11.60
12. 8
13. 20°
14.π m2
15. 3
16.2
17.证明:∵AB为⊙O的直径,∴∠ACB=90°,∠BCD与∠ACE互余,又∠ACE与∠CAE互余,∴∠BCD=∠BAC.∵OA=OC,∴∠OAC=∠OCA,∴∠ACO=∠BCD
18.解:过点C作CH⊥AB交AB于点H,∵AC=4,BC=3,∠C=90°,∴AB==5.∵S△ABC一定,∴AC·BC=AB·CH,∴CH=.∴BH==.∴AD=AB-2BH=.
19. 解:(1)连接OC,∵∠AOB=120°,C是的中点,∴∠AOC=∠BOC=60°.∵OA=OC,∴△ACO是等边三角形,∴OA=AC,同理OB=BC,∴OA=AC=BC=OB,∴四边形AOBC是菱形,∴AB平分∠OAC (2)∵C是的中点,由(1)知AC=AO,∴AP=AC,∴∠APC=30°,∴△OPC是直角三角形,∴PC=OC=
20.解:(1)连接OA,∵PA是⊙O的切线,∴∠PAO=90°,∵∠P=30°,∴∠AOD=60°,∵AC⊥PB,PB过圆心O,∴AD=DC.在Rt△ODA中,AD=OA·sin 60°=5×=,∴AC=2AD=5
(2)∵AC⊥PB,∠P=30°,∴∠PAC=60°.∵∠AOP=60°,∴∠BOA=120°,∴∠BCA=60°,∴∠PAC=∠BCA,∴BC∥PA
21.解:(1)如图,连接PD,PC.∵OB,OA,AB是⊙P的切线,∴BE=BD=6,AE=AC=4,OD=OC,PD⊥OB,PC⊥OC,又∵∠DOC=90°,DP=CP,∴四边形PDOC是正方形,∴PD=DO=OC=PC.设PD=x,∵OB2+OA2=AB2,AB=BE+AE=6+4=10,∴(x+6)2+(x+4)2=102,解得x1=2,x2=-12(舍去),∴⊙P的半径为2.
(2)如图,作EH⊥OA于H,∴EH∥OB,∴△ABO∽△AEH,∴==,∴==,∴EH=,AH=,∴OH=2+4-=,∴E.
22. 解:(1) 120°,60°
(2)作A2M⊥A1A3于M,如图1,根据正六边形的性质得:对角线A1A5=A2A4=A1A3,A1A2=A3A2,∠A1A2A3=120°,∴A1M=A3M,∠1=30°,∴A2M=A1A2=1,由勾股定理得:A1M==,∴A1A5=A2A4=A1A3=2
(3)连接A1A5,A1A4,A1A3,作A6C⊥A1A5,如图2,由(2)得:A6C=A1A6=1,A1C=,∴A1A5=A1A3=2,当A1第一次滚动到图2位置时,顶点A1所经过的路径分别是以A6,A5,A4,A3,A2为圆心,以2,2,4,2,2为半径,圆心角都为60°的五条弧,∴顶点A1所经过的路径的长=++++==π
第三章 圆
单元复习训练卷
一、选择题(共10小题,4*10=40)
1. 已知⊙O的半径为5,点P到圆心O的距离为6,那么点P与⊙O的位置关系是( )
A.点P在⊙O外
B.点P在⊙O内
C.点P在⊙O上
D.无法确定
2. 已知⊙O的半径为5 cm,圆心O到直线l的距离为5 cm,则直线l与⊙O的位置关系为( )
A.相交 B.相切
C.相离 D.无法确定
3. 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. B.2 C.2 D.8
4. 两圆既不相交又不相切,半径分别为3和5,则两圆的圆心距d的取值范围是( )
A. d>8 B. 0<d≤2
C. 2<d<8 D. 0≤d<2或d>8
5. 如图,直线l与⊙O相交于A,B两点,且与半径OC垂直,垂足为H,已知AB=16cm,sin∠OBH=,则⊙O的半径为( )
A.6cm B.10cm C.12cm D.cm
6. 用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(如图),则这个纸帽的底面周长是( )
A.2π cm B.3π cm C.4π cm D.5π cm
7. 如图,AB为⊙O的直径,AD切⊙O于点A,=.则下列结论不一定正确的是( )
A.BA⊥DA B.OC∥AE
C.∠COE=2∠CAE D.OD⊥AC
8. 如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图像被⊙P截得的弦AB的长为4,则a的值是( )
A.4 B.3+ C.3 D.3+
9.如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
A.130° B.100° C.65° D.50°
10. 如图,在边长为2的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是( )
A.2 B. C. D.1
二.填空题(共6小题,4*6=24)
11. 如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若∠AOB=120°,则∠ACB= .
12. 如图,P为⊙O外一点,PA,PB分别切⊙O于点A,B,CD切⊙O于点E且分别交PA,PB于点C,D,若PA=4,则△PCD的周长为_______.
13. 如图,已知PA,PB是⊙O的切线,A. B为切点,AC是⊙O的直径,∠P=40°,则∠BAC度数是 ;
14. 如图,一根5 m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊(羊只能在草地上活动),那么小羊在草地上的最大活动区域的面积是________.
15..如图,CD是☉O的直径,点A是半圆上的三等分点,B是的中点,P为直线CD上的一个动点,当CD=6时,AP+BP的最小值为 .
16.如图,直线l与半径为4的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l,垂足为B,连结PA.设PA=x,PB=y,则x-y的最大值是________.
三.解答题(共5小题, 56分)
17.(6分) 如图,AB为⊙O的直径,CD是弦,且AB⊥CD于点E,连接AC,OC,BC.求证:∠ACO=∠BCD.
18.(8分) 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,以点C为圆心,BC为半径作圆交AB于点D,求AD的长.
19.(8分) 如图,A,B是⊙O上的两点,∠AOB=120°,C是的中点.
(1)求证:AB平分∠OAC;
(2)延长OA至点P,使OA=AP,连接PC,若⊙O的半径R=1,求PC的长.
20.(10分) 如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C,交PB于点D,连接BC,当∠P=30°时:
(1)求弦AC的长;
(2)求证:BC∥PA.
21.(12分) 如图,有一个圆O和两个正六边形T1,T2,T1的六个顶点都在圆周上,T2的六条边都和圆O相切(称T1,T2分别为圆O的内接正六边形和外切正六边形).
(1)设T1,T2的边长分别为a,b,圆O的半径为r,求r:a与r:b;
(2)设正六边形T1的面积为S1,正六边形T2的面积为S2,求S1:S2.
22.(12分) 如图,将边长为2的正六边形A1A2A3A4A5A6在直线l上由图1的位置按顺时针方向向右作无滑动滚动.
(1)该正六边形的每一个内角的度数是________,每一个外角的度数为________;
(2)求它的对角线A1A5,A2A4,A1A3的长;
(3)直接写出点A1从图1滚动到图2的位置时,顶点A1所经过的路径长.
参考答案
1-5ABCDB 6-10CDBCD
11.60
12. 8
13. 20°
14.π m2
15. 3
16.2
17.证明:∵AB为⊙O的直径,∴∠ACB=90°,∠BCD与∠ACE互余,又∠ACE与∠CAE互余,∴∠BCD=∠BAC.∵OA=OC,∴∠OAC=∠OCA,∴∠ACO=∠BCD
18.解:过点C作CH⊥AB交AB于点H,∵AC=4,BC=3,∠C=90°,∴AB==5.∵S△ABC一定,∴AC·BC=AB·CH,∴CH=.∴BH==.∴AD=AB-2BH=.
19. 解:(1)连接OC,∵∠AOB=120°,C是的中点,∴∠AOC=∠BOC=60°.∵OA=OC,∴△ACO是等边三角形,∴OA=AC,同理OB=BC,∴OA=AC=BC=OB,∴四边形AOBC是菱形,∴AB平分∠OAC (2)∵C是的中点,由(1)知AC=AO,∴AP=AC,∴∠APC=30°,∴△OPC是直角三角形,∴PC=OC=
20.解:(1)连接OA,∵PA是⊙O的切线,∴∠PAO=90°,∵∠P=30°,∴∠AOD=60°,∵AC⊥PB,PB过圆心O,∴AD=DC.在Rt△ODA中,AD=OA·sin 60°=5×=,∴AC=2AD=5
(2)∵AC⊥PB,∠P=30°,∴∠PAC=60°.∵∠AOP=60°,∴∠BOA=120°,∴∠BCA=60°,∴∠PAC=∠BCA,∴BC∥PA
21.解:(1)如图,连接PD,PC.∵OB,OA,AB是⊙P的切线,∴BE=BD=6,AE=AC=4,OD=OC,PD⊥OB,PC⊥OC,又∵∠DOC=90°,DP=CP,∴四边形PDOC是正方形,∴PD=DO=OC=PC.设PD=x,∵OB2+OA2=AB2,AB=BE+AE=6+4=10,∴(x+6)2+(x+4)2=102,解得x1=2,x2=-12(舍去),∴⊙P的半径为2.
(2)如图,作EH⊥OA于H,∴EH∥OB,∴△ABO∽△AEH,∴==,∴==,∴EH=,AH=,∴OH=2+4-=,∴E.
22. 解:(1) 120°,60°
(2)作A2M⊥A1A3于M,如图1,根据正六边形的性质得:对角线A1A5=A2A4=A1A3,A1A2=A3A2,∠A1A2A3=120°,∴A1M=A3M,∠1=30°,∴A2M=A1A2=1,由勾股定理得:A1M==,∴A1A5=A2A4=A1A3=2
(3)连接A1A5,A1A4,A1A3,作A6C⊥A1A5,如图2,由(2)得:A6C=A1A6=1,A1C=,∴A1A5=A1A3=2,当A1第一次滚动到图2位置时,顶点A1所经过的路径分别是以A6,A5,A4,A3,A2为圆心,以2,2,4,2,2为半径,圆心角都为60°的五条弧,∴顶点A1所经过的路径的长=++++==π
