2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第二十九章投影与视图单元测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 266.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 23:48:16 | ||
图片预览


文档简介
人教版九年级数学下册
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 在同一时刻,两根长度相等的标杆被放置于阳光之下,但它们的影长不相等,那么这两根标杆的放置情况是( )
A.两根标杆直立在水平地面上
B.两根标杆平行地放在水平地面上
C.一定是一根标杆直立在地面上,另一根标杆平放在地面上
D.两根标杆放置的方向不平行
2. 人离窗子越远,向外眺望时此人的盲区是
A. 变小 B. 变大
C. 不变 D. 以上都有可能
3. 在阳光的照射下,一个矩形框的影子的形状不可能是( )
A.线段 B.平行四边形
C.等腰梯形 D.矩形
4. 下列立体图形中,俯视图与主视图不同的是( )
5. 王丽同学在某天下午的不同时刻拍了三张同一景物的风景照A,B,C,冲洗后不知道拍照的顺序,已知投影lA>lC>lB,则A,B,C的先后顺序是( )
A.A,B,C B.A,C,B
C.B,C,A D.B,A,C
6. 已知O为圆锥的顶点,M为底面圆周上一点,点P在OM上,一只蚂蚁从点P出发绕圆锥侧面爬行回到P时,所经过的最短路径的痕迹如图所示,若沿OM将圆锥侧面剪开并展平,则所得的侧面展开图是( )
7. 路边有一根电线杆AB和一块正方形广告牌CDFH,在某一时刻,小明发现在太阳光照射下,电线杆顶端A的影子刚好落在HF的中点G处,而正方形广告牌顶端上的F点的影子刚好落在地面上的E点(如图),已知BC=5米,正方形边长为3米,DE=4米,则电线杆的高度约是( )
A.8米 B.7米
C.6米 D.7.9米
8. 如图是某几何体的三视图,则该几何体是 ( )
A.长方体 B.正方体
C.三棱柱 D.圆柱
9.如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处径直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )
10. 由一些完全相同的小正方体搭成的几何体的主视图、俯视图如图所示,那么搭成这个几何体至少需用小正方体的个数是( )
A.8个 B.7个
C.6个 D.5个
二.填空题(共6小题,4*6=24)
11. 如果一个几何体的主视图、左视图及俯视图都全等,那么这个几何体既有可能是__ __,又有可能是__ __.
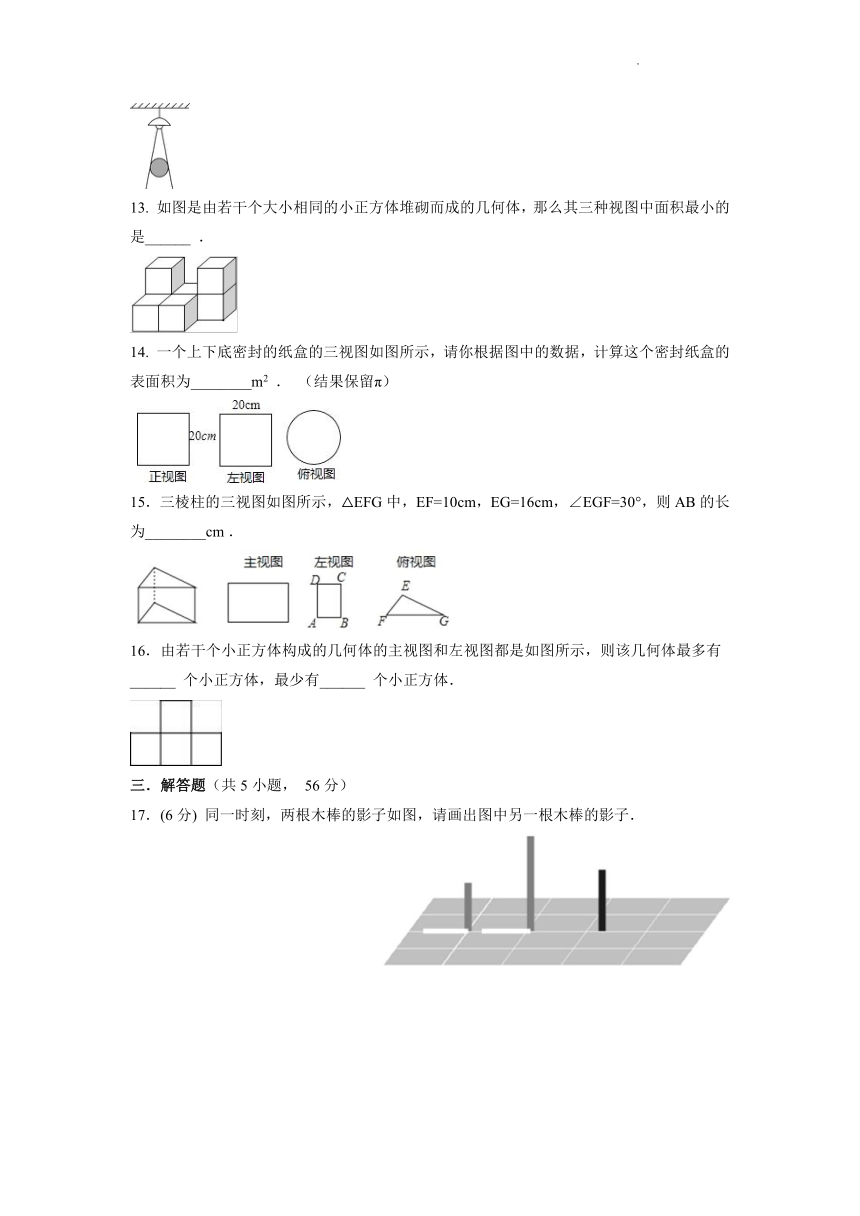
12. 如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把球向远离灯的位置移动时,圆形阴影面积的大小的变化情况是________.
13. 如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是______ .
14. 一个上下底密封的纸盒的三视图如图所示,请你根据图中的数据,计算这个密封纸盒的表面积为________m2 . (结果保留π)
15.三棱柱的三视图如图所示,△EFG中,EF=10cm,EG=16cm,∠EGF=30°,则AB的长为________cm .
16.由若干个小正方体构成的几何体的主视图和左视图都是如图所示,则该几何体最多有______ 个小正方体,最少有______ 个小正方体.
三.解答题(共5小题, 56分)
17.(6分) 同一时刻,两根木棒的影子如图,请画出图中另一根木棒的影子.
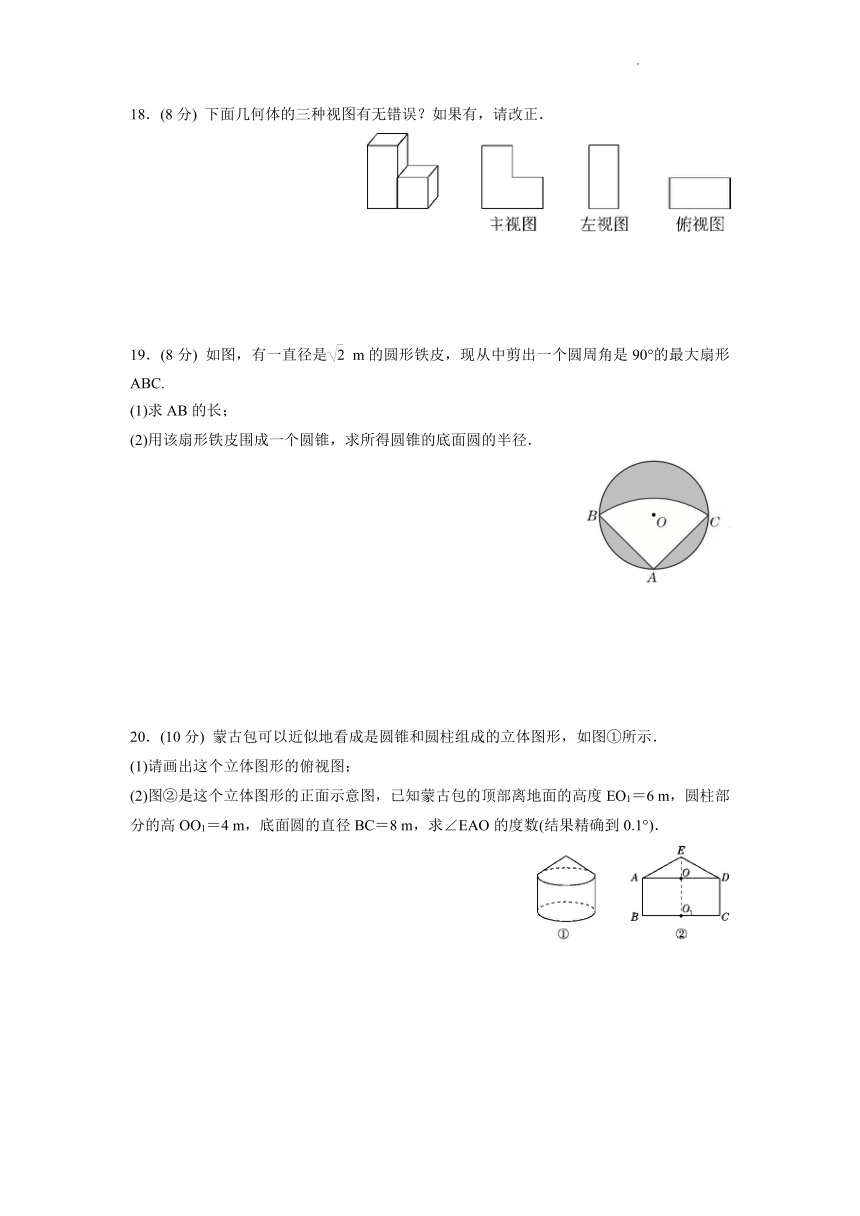
18.(8分) 下面几何体的三种视图有无错误?如果有,请改正.
19.(8分) 如图,有一直径是 m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC.
(1)求AB的长;
(2)用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.
20.(10分) 蒙古包可以近似地看成是圆锥和圆柱组成的立体图形,如图①所示.
(1)请画出这个立体图形的俯视图;
(2)图②是这个立体图形的正面示意图,已知蒙古包的顶部离地面的高度EO1=6 m,圆柱部分的高OO1=4 m,底面圆的直径BC=8 m,求∠EAO的度数(结果精确到0.1°).
21.(12分) 如图,花丛中有一根路灯杆AB,在灯光下小明在点D处的影长DE=3 m,沿BD方向行走到达点G,测得DG=5 m,这时小明的影长GH=5 m.如果小明的身高为1.7 m,求路灯杆AB的高度.
22.(12分) 某兴趣小组开展课外活动,如图,A,B两地相距12 m,小明从点A出发沿AB方向匀速前进,2 s后到达点D,此时他(CD)在某一灯光下的影子为AD,继续按原速行走2 s到达点F,此时他(EF)在同一灯光下的影子仍落在其身后,并测得这个影长为1.2 m,然后他将速度提高到原来的1.5倍,再行走2 s到达点H,此时他(GH)在同一灯光下的影子为BH.(点C,E,G在一条直线上)
(1)请在图中画出光源O的位置,并画出小明位于点F时在这个灯光下的影子FM(不写画法);
(2)求小明原来的速度.
参考答案
1-5DBCCC 6-10DDBCA
11.球,正方体
12.变小
13. 左视图
14.600π
15.8
16. 10,4
17. 解:如图所示:分别过木桩的顶端和它影子的顶端作直线,会发现两直线交于一点A,再过A、B画直线可得另一根木棒的影子.
18.解:有错误.主视图错,中间应画一条实线;左视图错,中间应画一条虚线;俯视图错,中间应画一条实线,如图所示.
19. 解:(1)连接BC.∵∠BAC=90°,∴BC为⊙O的直径,即BC= m,∴AB=BC=1 m.
(2)设所得圆锥的底面圆的半径为r m,根据题意得2πr=,解得r=.∴所得圆锥的底面圆的半径为 m.
20.解:(1)俯视图如图所示.
(2)∵EO1=6 m,OO1=4 m,∴EO=EO1-OO1=6-4=2(m),∵AD=BC=8 m,∴OA=OD=4 m,在Rt△AOE中,tan ∠EAO===,则∠EAO≈26.6°.
21. 解:由题意,得AB⊥BH,CD⊥BH,FG⊥BH.在△ABE和△CDE中,∵AB⊥BH,CD⊥BH,∴CD∥AB.∴△ABE∽△CDE.∴=.同理可得△ABH∽△FGH,∴=.又∵CD=FG=1.7 m,∴=.∵DE=3 m,DG=5 m,GH=5 m,∴=,解得BD=7.5 m.∴AB===5.95(m).答:路灯杆AB的高度为5.95 m.
22. 解:(1)如图.
(2)设小明原来的速度为x m/s,则CE=2x m,AM=AF-MF=(4x-1.2)m,EG=2×1.5x=3x(m),BM=AB-AM=12-(4x-1.2)=(13.2-4x)m.由题易知△OCE∽△OAM,△OEG∽△OMB. ∴=,=.∴=,即=.解得x1=1.5,x2=0,经检验x1=1.5,x2=0都为方程的解,但x2=0不符合题意,舍去,∴x=1.5,即小明原来的速度为1.5 m/s.
第二十九章 投影与视图
单元测试训练卷
一、选择题(共10小题,4*10=40)
1. 在同一时刻,两根长度相等的标杆被放置于阳光之下,但它们的影长不相等,那么这两根标杆的放置情况是( )
A.两根标杆直立在水平地面上
B.两根标杆平行地放在水平地面上
C.一定是一根标杆直立在地面上,另一根标杆平放在地面上
D.两根标杆放置的方向不平行
2. 人离窗子越远,向外眺望时此人的盲区是
A. 变小 B. 变大
C. 不变 D. 以上都有可能
3. 在阳光的照射下,一个矩形框的影子的形状不可能是( )
A.线段 B.平行四边形
C.等腰梯形 D.矩形
4. 下列立体图形中,俯视图与主视图不同的是( )
5. 王丽同学在某天下午的不同时刻拍了三张同一景物的风景照A,B,C,冲洗后不知道拍照的顺序,已知投影lA>lC>lB,则A,B,C的先后顺序是( )
A.A,B,C B.A,C,B
C.B,C,A D.B,A,C
6. 已知O为圆锥的顶点,M为底面圆周上一点,点P在OM上,一只蚂蚁从点P出发绕圆锥侧面爬行回到P时,所经过的最短路径的痕迹如图所示,若沿OM将圆锥侧面剪开并展平,则所得的侧面展开图是( )
7. 路边有一根电线杆AB和一块正方形广告牌CDFH,在某一时刻,小明发现在太阳光照射下,电线杆顶端A的影子刚好落在HF的中点G处,而正方形广告牌顶端上的F点的影子刚好落在地面上的E点(如图),已知BC=5米,正方形边长为3米,DE=4米,则电线杆的高度约是( )
A.8米 B.7米
C.6米 D.7.9米
8. 如图是某几何体的三视图,则该几何体是 ( )
A.长方体 B.正方体
C.三棱柱 D.圆柱
9.如图,在一条笔直的小路上有一盏路灯,晚上小雷从点B处径直走到点A处时,小雷在灯光照射下的影长y与行走的路程x之间的函数图象大致是( )
10. 由一些完全相同的小正方体搭成的几何体的主视图、俯视图如图所示,那么搭成这个几何体至少需用小正方体的个数是( )
A.8个 B.7个
C.6个 D.5个
二.填空题(共6小题,4*6=24)
11. 如果一个几何体的主视图、左视图及俯视图都全等,那么这个几何体既有可能是__ __,又有可能是__ __.
12. 如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把球向远离灯的位置移动时,圆形阴影面积的大小的变化情况是________.
13. 如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是______ .
14. 一个上下底密封的纸盒的三视图如图所示,请你根据图中的数据,计算这个密封纸盒的表面积为________m2 . (结果保留π)
15.三棱柱的三视图如图所示,△EFG中,EF=10cm,EG=16cm,∠EGF=30°,则AB的长为________cm .
16.由若干个小正方体构成的几何体的主视图和左视图都是如图所示,则该几何体最多有______ 个小正方体,最少有______ 个小正方体.
三.解答题(共5小题, 56分)
17.(6分) 同一时刻,两根木棒的影子如图,请画出图中另一根木棒的影子.
18.(8分) 下面几何体的三种视图有无错误?如果有,请改正.
19.(8分) 如图,有一直径是 m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC.
(1)求AB的长;
(2)用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.
20.(10分) 蒙古包可以近似地看成是圆锥和圆柱组成的立体图形,如图①所示.
(1)请画出这个立体图形的俯视图;
(2)图②是这个立体图形的正面示意图,已知蒙古包的顶部离地面的高度EO1=6 m,圆柱部分的高OO1=4 m,底面圆的直径BC=8 m,求∠EAO的度数(结果精确到0.1°).
21.(12分) 如图,花丛中有一根路灯杆AB,在灯光下小明在点D处的影长DE=3 m,沿BD方向行走到达点G,测得DG=5 m,这时小明的影长GH=5 m.如果小明的身高为1.7 m,求路灯杆AB的高度.
22.(12分) 某兴趣小组开展课外活动,如图,A,B两地相距12 m,小明从点A出发沿AB方向匀速前进,2 s后到达点D,此时他(CD)在某一灯光下的影子为AD,继续按原速行走2 s到达点F,此时他(EF)在同一灯光下的影子仍落在其身后,并测得这个影长为1.2 m,然后他将速度提高到原来的1.5倍,再行走2 s到达点H,此时他(GH)在同一灯光下的影子为BH.(点C,E,G在一条直线上)
(1)请在图中画出光源O的位置,并画出小明位于点F时在这个灯光下的影子FM(不写画法);
(2)求小明原来的速度.
参考答案
1-5DBCCC 6-10DDBCA
11.球,正方体
12.变小
13. 左视图
14.600π
15.8
16. 10,4
17. 解:如图所示:分别过木桩的顶端和它影子的顶端作直线,会发现两直线交于一点A,再过A、B画直线可得另一根木棒的影子.
18.解:有错误.主视图错,中间应画一条实线;左视图错,中间应画一条虚线;俯视图错,中间应画一条实线,如图所示.
19. 解:(1)连接BC.∵∠BAC=90°,∴BC为⊙O的直径,即BC= m,∴AB=BC=1 m.
(2)设所得圆锥的底面圆的半径为r m,根据题意得2πr=,解得r=.∴所得圆锥的底面圆的半径为 m.
20.解:(1)俯视图如图所示.
(2)∵EO1=6 m,OO1=4 m,∴EO=EO1-OO1=6-4=2(m),∵AD=BC=8 m,∴OA=OD=4 m,在Rt△AOE中,tan ∠EAO===,则∠EAO≈26.6°.
21. 解:由题意,得AB⊥BH,CD⊥BH,FG⊥BH.在△ABE和△CDE中,∵AB⊥BH,CD⊥BH,∴CD∥AB.∴△ABE∽△CDE.∴=.同理可得△ABH∽△FGH,∴=.又∵CD=FG=1.7 m,∴=.∵DE=3 m,DG=5 m,GH=5 m,∴=,解得BD=7.5 m.∴AB===5.95(m).答:路灯杆AB的高度为5.95 m.
22. 解:(1)如图.
(2)设小明原来的速度为x m/s,则CE=2x m,AM=AF-MF=(4x-1.2)m,EG=2×1.5x=3x(m),BM=AB-AM=12-(4x-1.2)=(13.2-4x)m.由题易知△OCE∽△OAM,△OEG∽△OMB. ∴=,=.∴=,即=.解得x1=1.5,x2=0,经检验x1=1.5,x2=0都为方程的解,但x2=0不符合题意,舍去,∴x=1.5,即小明原来的速度为1.5 m/s.
