2021--2022学年鲁教版(五四制)六年级数学下册第7章平行线的有关证明提升专题练习(Word版含答案)
文档属性
| 名称 | 2021--2022学年鲁教版(五四制)六年级数学下册第7章平行线的有关证明提升专题练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 144.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-27 23:48:59 | ||
图片预览



文档简介
鲁教版六年级下册数学《平行线的有关证明》知识点巩固与提升专题练习
一、选择题 .
1.如图所示,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是( )
A. 平行 B. 垂直 C. 平行或垂直 D. 无法确定
2. 如图,已知a,b,c,d四条直线,a∥b,c∥d,∠1=110°,则∠2等于 ( )
A.50° B.70° C.90° D.110°
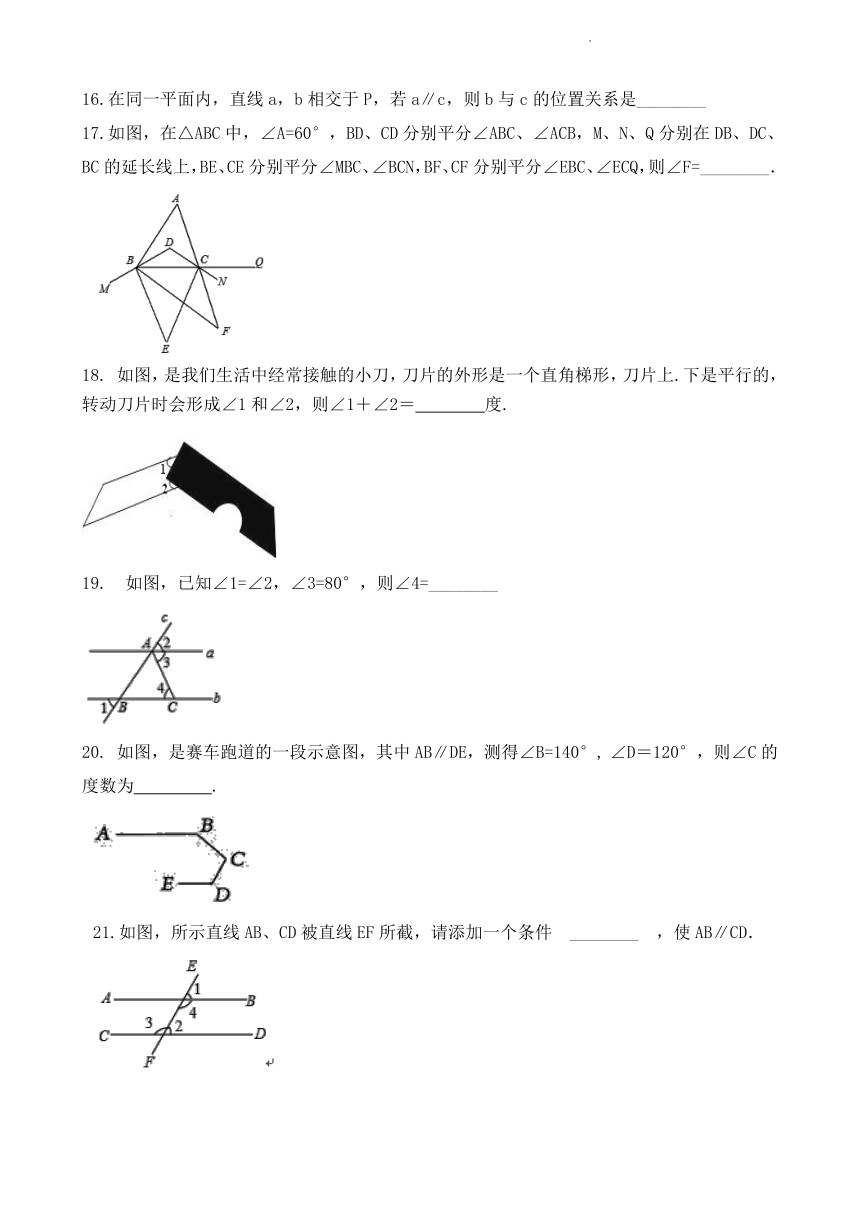
3. 下列命题中真命题的个数有( )
①小朋友荡秋千可以看做是平移运动;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④不是对顶角的角不相等.
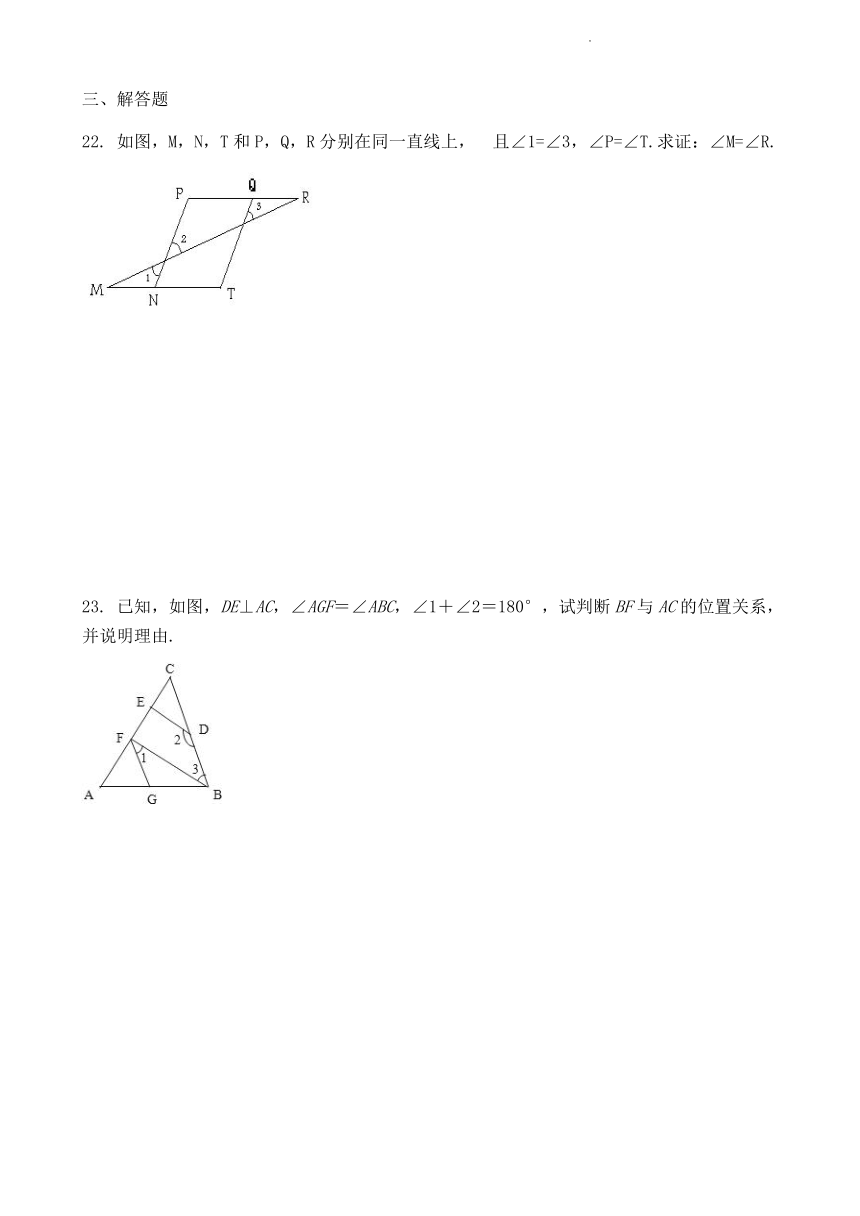
A. 1个 B. 2个 C. 3个 D. 4个
4.如图,下列条件:∠1=∠2;∠3=∠4;∠2+∠3=∠5;∠2+∠3+∠A=180°;∠4+∠1=∠5,能判定AB∥DC有( )
A. 3个 B. 4个 C. 5个 D. 6个
5. 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是 ( )
A.40° B.70° C.80° D.140°
6. 如图,已知a∥b,∠1=50°,∠2=90°,则∠3的度数为( )
A.40° B.50° C.150° D.140°
7.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
A. 15° B. 30° C. 45° D. 60°
8. 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为 ( )
A.65° B.55° C.45° D.35°
9.如图,四边形ABCD , E 是CB 延长线上一点,下列推理正确的是( )
A. 如果∠1=∠2 ,那么AB∥CD
B. 如果∠3=∠4 ,那么 AD∥BC
C. 如果AD∥BC , 那么∠6+∠BAD=180°.
D. 如果∠6+∠BCD=180°,那么AD∥BC
10. 如图,将一块直角三角板的直角顶点放在直尺的一边上.如果∠1=50°,那么∠2的度数是 ( )
A.30° B.40° C.50° D.60°
二、填空题
11. 如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2=________.
12.已知,在△ABC中,∠A=80°,那么∠B=∠C=________度.
13. 如图,AB∥CD,AE交CD于点C,DE⊥AE于点E,若∠A=42°,则∠D=________.
14.三角形的内角和是 ________度.
15. 如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=42°,
则∠2=________.
16.在同一平面内,直线a,b相交于P,若a∥c,则b与c的位置关系是________
17.如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.
18. 如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上.下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2= 度.
19. 如图,已知∠1=∠2,∠3=80°,则∠4=________
20. 如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°, ∠D=120°,则∠C的度数为 .
21.如图,所示直线AB、CD被直线EF所截,请添加一个条件 ________ ,使AB∥CD.
三、解答题
22. 如图,M,N,T和P,Q,R分别在同一直线上, 且∠1=∠3,∠P=∠T.求证:∠M=∠R.
23. 已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
24.如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?________;(请直接写出答案)
(3)如图3,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由.
鲁教版六年级下册数学《平行线的有关证明》知识点巩固与提升专题练习
(答案版)
一、选择题 .
1.如图所示,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是( C )
A. 平行 B. 垂直 C. 平行或垂直 D. 无法确定
2. 如图,已知a,b,c,d四条直线,a∥b,c∥d,∠1=110°,则∠2等于 ( B )
A.50° B.70° C.90° D.110°
3. 下列命题中真命题的个数有( A )
①小朋友荡秋千可以看做是平移运动;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④不是对顶角的角不相等.
A. 1个 B. 2个 C. 3个 D. 4个
4.如图,下列条件:∠1=∠2;∠3=∠4;∠2+∠3=∠5;∠2+∠3+∠A=180°;∠4+∠1=∠5,能判定AB∥DC有( A )
A. 3个 B. 4个 C. 5个 D. 6个
5. 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是 ( B )
A.40° B.70° C.80° D.140°
6. 如图,已知a∥b,∠1=50°,∠2=90°,则∠3的度数为( D )
A.40° B.50° C.150° D.140°
7.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( A )
A. 15° B. 30° C. 45° D. 60°
8. 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为 ( B )
A.65° B.55° C.45° D.35°
9.如图,四边形ABCD , E 是CB 延长线上一点,下列推理正确的是( C )
A. 如果∠1=∠2 ,那么AB∥CD
B. 如果∠3=∠4 ,那么 AD∥BC
C. 如果AD∥BC , 那么∠6+∠BAD=180°.
D. 如果∠6+∠BCD=180°,那么AD∥BC
10. 如图,将一块直角三角板的直角顶点放在直尺的一边上.如果∠1=50°,那么∠2的度数是 ( B )
A.30° B.40° C.50° D.60°
二、填空题
11. 如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2=________.
答案:65°
12.已知,在△ABC中,∠A=80°,那么∠B=∠C=________度.
答案:50
13. 如图,AB∥CD,AE交CD于点C,DE⊥AE于点E,若∠A=42°,则∠D=________.
答案:48°
14.三角形的内角和是 ________度.
答案:180
15. 如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=42°,
则∠2=________.
答案:159°
16.在同一平面内,直线a,b相交于P,若a∥c,则b与c的位置关系是________
答案:相交
17.如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.
答案:15°
18. 如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上.下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2= 度.
答案:90
19. 如图,已知∠1=∠2,∠3=80°,则∠4=________
答案; 80°
20. 如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°, ∠D=120°,则∠C的度数为 .
答案;100°
21.如图,所示直线AB、CD被直线EF所截,请添加一个条件 ________ ,使AB∥CD.
答案: ∠1=∠2
三、解答题
22. 如图,M,N,T和P,Q,R分别在同一直线上, 且∠1=∠3,∠P=∠T.求证:∠M=∠R.
证明:∵∠1=∠3,∠1=∠2,
∴∠2=∠3,
∴PN∥QT,
∴∠T=∠MNP.
∵∠P=∠T,
∴∠P=∠MNP,
∴PR∥MT,
∴∠M=∠R..
23. 已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
解:BF⊥AC.理由如下:
∵∠AGF=∠ABC,
∴FG∥BC,
∴∠1=∠3.
∵∠1+∠2=180°,∠3+∠2=180°,
∴BF∥DE,
∴∠BFC=∠DEC.
∵DE⊥AC,
∴∠DEC=90°,
∴∠BFC=90°,
∴BF⊥AC.
24.如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?________;(请直接写出答案)
(3)如图3,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由.
(1)解:AB∥CD. 理由:∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE,
∵∠EAC+∠ACE=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD
(2)∠BAC=∠PQC+∠QPC
(3)解:∠BAE+ ∠MCD=90°. 如图3,过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE,
∵∠E=90°,
∴∠BAE+∠ECD=90°,
∵∠MCE=∠ECD,
∴∠BAE+ ∠MCD=90°.
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
一、选择题 .
1.如图所示,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是( )
A. 平行 B. 垂直 C. 平行或垂直 D. 无法确定
2. 如图,已知a,b,c,d四条直线,a∥b,c∥d,∠1=110°,则∠2等于 ( )
A.50° B.70° C.90° D.110°
3. 下列命题中真命题的个数有( )
①小朋友荡秋千可以看做是平移运动;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④不是对顶角的角不相等.
A. 1个 B. 2个 C. 3个 D. 4个
4.如图,下列条件:∠1=∠2;∠3=∠4;∠2+∠3=∠5;∠2+∠3+∠A=180°;∠4+∠1=∠5,能判定AB∥DC有( )
A. 3个 B. 4个 C. 5个 D. 6个
5. 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是 ( )
A.40° B.70° C.80° D.140°
6. 如图,已知a∥b,∠1=50°,∠2=90°,则∠3的度数为( )
A.40° B.50° C.150° D.140°
7.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
A. 15° B. 30° C. 45° D. 60°
8. 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为 ( )
A.65° B.55° C.45° D.35°
9.如图,四边形ABCD , E 是CB 延长线上一点,下列推理正确的是( )
A. 如果∠1=∠2 ,那么AB∥CD
B. 如果∠3=∠4 ,那么 AD∥BC
C. 如果AD∥BC , 那么∠6+∠BAD=180°.
D. 如果∠6+∠BCD=180°,那么AD∥BC
10. 如图,将一块直角三角板的直角顶点放在直尺的一边上.如果∠1=50°,那么∠2的度数是 ( )
A.30° B.40° C.50° D.60°
二、填空题
11. 如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2=________.
12.已知,在△ABC中,∠A=80°,那么∠B=∠C=________度.
13. 如图,AB∥CD,AE交CD于点C,DE⊥AE于点E,若∠A=42°,则∠D=________.
14.三角形的内角和是 ________度.
15. 如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=42°,
则∠2=________.
16.在同一平面内,直线a,b相交于P,若a∥c,则b与c的位置关系是________
17.如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.
18. 如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上.下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2= 度.
19. 如图,已知∠1=∠2,∠3=80°,则∠4=________
20. 如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°, ∠D=120°,则∠C的度数为 .
21.如图,所示直线AB、CD被直线EF所截,请添加一个条件 ________ ,使AB∥CD.
三、解答题
22. 如图,M,N,T和P,Q,R分别在同一直线上, 且∠1=∠3,∠P=∠T.求证:∠M=∠R.
23. 已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
24.如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?________;(请直接写出答案)
(3)如图3,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由.
鲁教版六年级下册数学《平行线的有关证明》知识点巩固与提升专题练习
(答案版)
一、选择题 .
1.如图所示,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是( C )
A. 平行 B. 垂直 C. 平行或垂直 D. 无法确定
2. 如图,已知a,b,c,d四条直线,a∥b,c∥d,∠1=110°,则∠2等于 ( B )
A.50° B.70° C.90° D.110°
3. 下列命题中真命题的个数有( A )
①小朋友荡秋千可以看做是平移运动;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④不是对顶角的角不相等.
A. 1个 B. 2个 C. 3个 D. 4个
4.如图,下列条件:∠1=∠2;∠3=∠4;∠2+∠3=∠5;∠2+∠3+∠A=180°;∠4+∠1=∠5,能判定AB∥DC有( A )
A. 3个 B. 4个 C. 5个 D. 6个
5. 如图,直线AB∥CD,AE平分∠CAB.AE与CD相交于点E,∠ACD=40°,则∠BAE的度数是 ( B )
A.40° B.70° C.80° D.140°
6. 如图,已知a∥b,∠1=50°,∠2=90°,则∠3的度数为( D )
A.40° B.50° C.150° D.140°
7.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( A )
A. 15° B. 30° C. 45° D. 60°
8. 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为 ( B )
A.65° B.55° C.45° D.35°
9.如图,四边形ABCD , E 是CB 延长线上一点,下列推理正确的是( C )
A. 如果∠1=∠2 ,那么AB∥CD
B. 如果∠3=∠4 ,那么 AD∥BC
C. 如果AD∥BC , 那么∠6+∠BAD=180°.
D. 如果∠6+∠BCD=180°,那么AD∥BC
10. 如图,将一块直角三角板的直角顶点放在直尺的一边上.如果∠1=50°,那么∠2的度数是 ( B )
A.30° B.40° C.50° D.60°
二、填空题
11. 如图,直线AB∥CD,CA平分∠BCD,若∠1=50°,则∠2=________.
答案:65°
12.已知,在△ABC中,∠A=80°,那么∠B=∠C=________度.
答案:50
13. 如图,AB∥CD,AE交CD于点C,DE⊥AE于点E,若∠A=42°,则∠D=________.
答案:48°
14.三角形的内角和是 ________度.
答案:180
15. 如图,已知直线AB∥CD,∠GEB的平分线EF交CD于点F,∠1=42°,
则∠2=________.
答案:159°
16.在同一平面内,直线a,b相交于P,若a∥c,则b与c的位置关系是________
答案:相交
17.如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F=________.
答案:15°
18. 如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上.下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2= 度.
答案:90
19. 如图,已知∠1=∠2,∠3=80°,则∠4=________
答案; 80°
20. 如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°, ∠D=120°,则∠C的度数为 .
答案;100°
21.如图,所示直线AB、CD被直线EF所截,请添加一个条件 ________ ,使AB∥CD.
答案: ∠1=∠2
三、解答题
22. 如图,M,N,T和P,Q,R分别在同一直线上, 且∠1=∠3,∠P=∠T.求证:∠M=∠R.
证明:∵∠1=∠3,∠1=∠2,
∴∠2=∠3,
∴PN∥QT,
∴∠T=∠MNP.
∵∠P=∠T,
∴∠P=∠MNP,
∴PR∥MT,
∴∠M=∠R..
23. 已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
解:BF⊥AC.理由如下:
∵∠AGF=∠ABC,
∴FG∥BC,
∴∠1=∠3.
∵∠1+∠2=180°,∠3+∠2=180°,
∴BF∥DE,
∴∠BFC=∠DEC.
∵DE⊥AC,
∴∠DEC=90°,
∴∠BFC=90°,
∴BF⊥AC.
24.如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?________;(请直接写出答案)
(3)如图3,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD否存在确定的数量关系?并说明理由.
(1)解:AB∥CD. 理由:∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE,
∵∠EAC+∠ACE=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD
(2)∠BAC=∠PQC+∠QPC
(3)解:∠BAE+ ∠MCD=90°. 如图3,过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE,
∵∠E=90°,
∴∠BAE+∠ECD=90°,
∵∠MCE=∠ECD,
∴∠BAE+ ∠MCD=90°.
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
