山东省聊城市某重点高中2013届高三上学期第三次调研考试理科数学试题
文档属性
| 名称 | 山东省聊城市某重点高中2013届高三上学期第三次调研考试理科数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 207.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-14 00:00:00 | ||
图片预览



文档简介
山东省聊城市某重点高中2013届高三上学期第三次调研考试
理科数学试题
考试时间:100分钟;
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、选择题
1.方程组的解集是( )
A . B. C. D.
2.在平面直角坐标系xOy中,点A(5,0).对于某个正实数k,存在函数f(x)=ax2(a0),使得=·()(为常数),其中点P,Q的坐标分别为(1, f(1) ),(k, f(k)),则k的取值范围为( )
A.(2,+∞) B.(3,+∞)
C.[4,+∞) D.[8,+∞)
3.已知定义在R上的函数满足下列三个条件:
①对于任意的xR都有
②对于任意的;
③函数的图象关于y轴对称,则下列结论正确的是( )
A. B.
C. D.
4. 的展开式中的系数是( )
A. B. C.3 D.4
5.在下列关于直线于平面的命题中真命题是 ( )
A.若且,则 B.若且,则
C.若且,则 D.若且,则
6.数列{}前n项和是,如果,则这个数列是( )
A.等比数列 B.等差数列
C.除去第一项是等比 D.除去最后一项为等差
7.已知正四棱锥的侧棱长与底面边长都相等,是的中点,则所成的角的余弦值为( )
A. B. C. D.
8.若集合,则AB等
( )
A. B. C. D.
9.在△OAB中,O为坐标原点,A(1,cos),B(sin ,1),则△OAB的面积的取值范围是( )
A.(0,1] B.[,]
C.[,] D.[,]
10.连结球面上两点的线段称为球的弦。半径为4的球的两条弦、的长度分别等于、,、分别为、的中点,每条弦的两端都在球面上运动,有下列四个命题:
①弦、可能相交于点 ②弦、可能相交于点
③的最大值为5 ④的最小值为1
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
11.下列表示①②③ ④中,正确的个数为( )
A.1 B.2 C.3 D.4
12.已知两条直线m,n,两个平面,,给出下面四个命题:
①m∥n,mn;②∥,m,nm∥n;③m∥n,m∥n∥;④n∥,m∥n,mn其中真命题的序号是( )
A.①④ B.②④ C.①② D.②③
第II卷(非选择题)
二、填空题
13.已知函数,,则的最小正周期是 .
14.满足条件的三角形的面积的最大值
15.已知一个等差数列共有2 005项,那么它的偶数项之和与奇数项之和的比值是__________.
16.设直线和圆相交于点A、B,则弦AB的垂直平分线方程是 ___________________________.
三、解答题
17.求函数f(x)=ax+b在区间[m,n]上的平均变化率
18.如图,直三棱柱ABC—A1B1C1中ACB=90o,M,N分别为A1B,B1C1的中点.求证:
(1)BC∥平面MNB1:
(2)平面A1CB上平面ACC1A1.
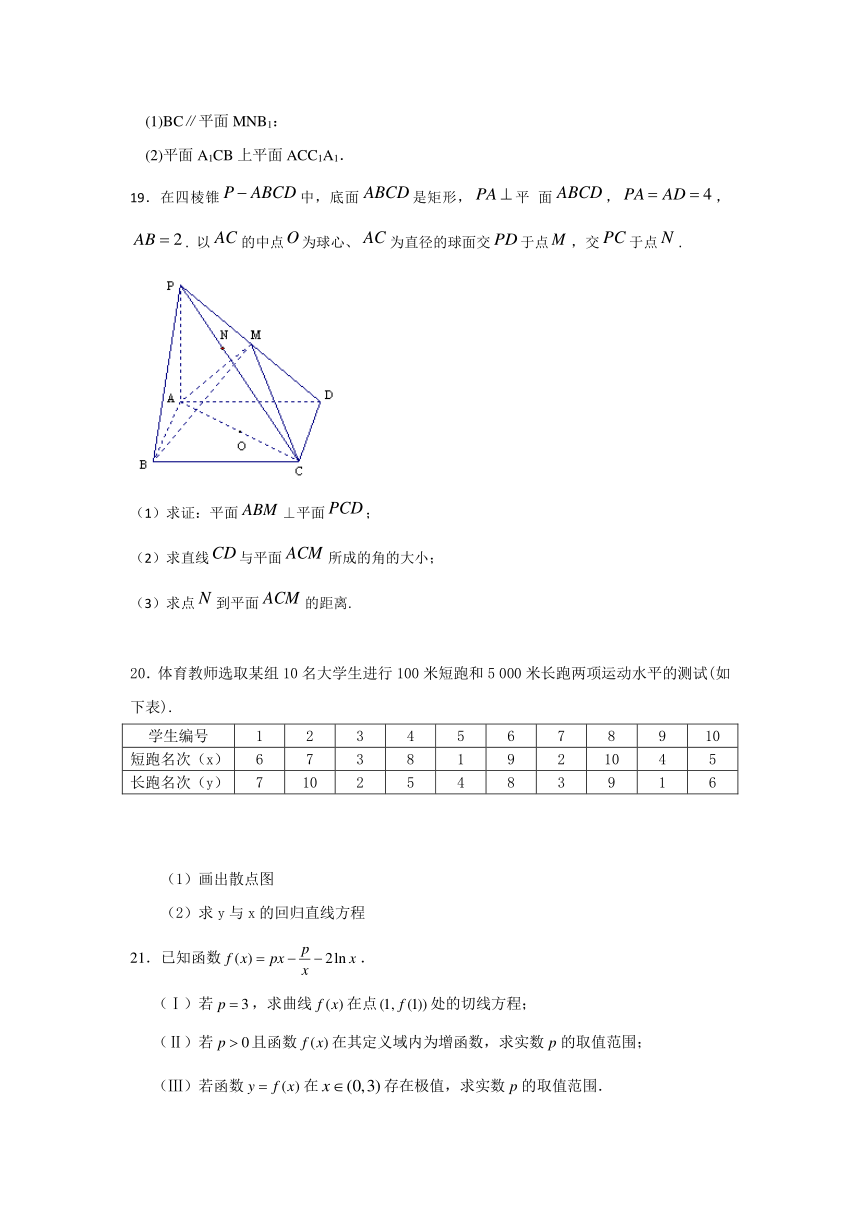
19.在四棱锥中,底面是矩形,平 面,,. 以的中点为球心、为直径的球面交于点,交于点.
(1)求证:平面⊥平面;
(2)求直线与平面所成的角的大小;
(3)求点到平面的距离.
20.体育教师选取某组10名大学生进行100米短跑和5 000米长跑两项运动水平的测试(如下表).
学生编号
1
2
3
4
5
6
7
8
9
10
短跑名次(x)
6
7
3
8
1
9
2
10
4
5
长跑名次(y)
7
10
2
5
4
8
3
9
1
6
(1)画出散点图
(2)求y与x的回归直线方程
21.已知函数.
(Ⅰ)若,求曲线在点处的切线方程;
(Ⅱ)若且函数在其定义域内为增函数,求实数的取值范围;
(Ⅲ)若函数在存在极值,求实数的取值范围.
22.写出下列命题的否定与否命题:
(1)等腰三角形有两个内角相等.
(2)可以被5整除的整数,末位是0.
(3)若xy=0,则x=0或y=0.
参考答案
一、选择题
1.C??????2.A??????
解析:如图所示, 设=,=,+=,则,= P(1, ),Q(k, k2 ), =(1,0), =(,), =(+1, ),则直线OG的方程为 y=x=,解得2 =1-, ||=1, 1-0,k2
3.A??????4.B??????
解析:
5.C??????6.A??????
解析:
7.C??????
解析:连接AC、BD交于O,连接OE,因OE∥SD.所以∠AEO为所求。设侧棱长与底面边长都等于2,则在⊿AEO中,OE=1,AO=,AE=, 于是
8.B??????9.D??????
解析:直线OA的方程是y=xcos,即xcos-y=0,点B到直线OA的距离d==,|OA|=,故 ? △OAB的面积|OA|·d= (1-sincos)=(1一sin2)[,].选D
10.C??????
解析:①③④正确,②错误.易求得、到球心的距离分别为3、2,若两弦交于,则⊥,中,有,矛盾。当、、共线时分别取最大值5最小值1.
11.A??????12.A??????
解析:∥,m,n.可能有m∥n,也可能有m与n异面,故②错;m∥n,m∥,则可能有n∥,也可能有n,故③错;易知①④正确,故选A
二、填空题
13.
14.
15.
16.
三、解答题
17.a
18.解:(1)因为BC∥B1 C1 ,且B1 C1 平面MNB1 ,BC平面MNB1 ,故BC∥平面MNB1 (2)因为BCAC,且ABC—A1 B1 C1 为直三棱柱, 故BC平面ACC1 A1 因为BC平面A1 CB, 故平面A1 CB平面ACC1 A1
19.方法一: ????? (1)依题设知,是所作球面的直径,则. ?????? 又因为平面,则,又, ?????? 所以平面,则,所以平面, ?????? 所以平面平面. ????? (2)由(1)知,,又,则是的中点 ?????? 可得, ?????? 则 ?????? 设到平面的距离为,由即, ?????? 可求得, ?????? 设所求角为,则,. ????? (3)可求得.因为,由,得.所以:????????? ?????? =:. ?????? 故点到平面的距离等于点到平面距离的. ?????? 又因为是的中点,则、到平面的距离相等,由(2)可知所求????????????? ?????? 距离为. ?? 方法二: (1)同方法一; (2)如图所示,建立空间直角坐标系,则,,,,,;设平面的一个法向量,由可得:,令,则.设所求角为,则,所以所求角的大小为. (3)由条件可得,在中,,所以,则,,所以所求距离等于点到平面距离的,设点到平面距离为则,所以所求距离为.
20.(1)略 (2)=0.745x+1.4
21. ????????????? (Ⅱ), ????????????? 要使在定义域内是增函数,只需在内恒成立 ????????????? 即在上恒成立, ????????????? (法一)即在上恒成立 ????????????? ∴,设 ????????????? 则 ????????????? ∵,∴ ,当且仅当时取等号 ????????????? ∴ ,即,∴ ????????????? 所以实数的取值范围是 (法二)令, 要使在定义域内是增函数,只需在内恒成立. 由题意,的图象为开口向上的抛物线, 对称轴方程为,∴, ∴, 解得 ∴实数的取值范围是.(Ⅲ)∵,令,即 设 当时,方程()的解为,此时在无极值, 所以; 当时,的对称轴方程为 ①若在恰好有一个极值 则 ,解得 ????????????? 此时在存在一个极大值;????????????? ????????????? ②若在恰好两个极值,即在有两个不等实根 ????????????? 则 或 ,解得????????????? ????????????? . ????????????? 综上所述,当时,在存在极值.
22.(1)命题的否定:存在一个等腰三角形,没有两个内角相等.否命题:若三角形不是等腰三角形,则它的任意两个内角都不相等. (2)命题的否定:存在一个可以被5整除的整数,其末位不是0.否命题:不能被5整除的整数,其末位不是0. (3)命题的否定:若xy=0,则x≠0且y≠0.否命题:若xy≠0,则x≠0且y≠0.
理科数学试题
考试时间:100分钟;
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、选择题
1.方程组的解集是( )
A . B. C. D.
2.在平面直角坐标系xOy中,点A(5,0).对于某个正实数k,存在函数f(x)=ax2(a0),使得=·()(为常数),其中点P,Q的坐标分别为(1, f(1) ),(k, f(k)),则k的取值范围为( )
A.(2,+∞) B.(3,+∞)
C.[4,+∞) D.[8,+∞)
3.已知定义在R上的函数满足下列三个条件:
①对于任意的xR都有
②对于任意的;
③函数的图象关于y轴对称,则下列结论正确的是( )
A. B.
C. D.
4. 的展开式中的系数是( )
A. B. C.3 D.4
5.在下列关于直线于平面的命题中真命题是 ( )
A.若且,则 B.若且,则
C.若且,则 D.若且,则
6.数列{}前n项和是,如果,则这个数列是( )
A.等比数列 B.等差数列
C.除去第一项是等比 D.除去最后一项为等差
7.已知正四棱锥的侧棱长与底面边长都相等,是的中点,则所成的角的余弦值为( )
A. B. C. D.
8.若集合,则AB等
( )
A. B. C. D.
9.在△OAB中,O为坐标原点,A(1,cos),B(sin ,1),则△OAB的面积的取值范围是( )
A.(0,1] B.[,]
C.[,] D.[,]
10.连结球面上两点的线段称为球的弦。半径为4的球的两条弦、的长度分别等于、,、分别为、的中点,每条弦的两端都在球面上运动,有下列四个命题:
①弦、可能相交于点 ②弦、可能相交于点
③的最大值为5 ④的最小值为1
其中真命题的个数为( )
A.1个 B.2个 C.3个 D.4个
11.下列表示①②③ ④中,正确的个数为( )
A.1 B.2 C.3 D.4
12.已知两条直线m,n,两个平面,,给出下面四个命题:
①m∥n,mn;②∥,m,nm∥n;③m∥n,m∥n∥;④n∥,m∥n,mn其中真命题的序号是( )
A.①④ B.②④ C.①② D.②③
第II卷(非选择题)
二、填空题
13.已知函数,,则的最小正周期是 .
14.满足条件的三角形的面积的最大值
15.已知一个等差数列共有2 005项,那么它的偶数项之和与奇数项之和的比值是__________.
16.设直线和圆相交于点A、B,则弦AB的垂直平分线方程是 ___________________________.
三、解答题
17.求函数f(x)=ax+b在区间[m,n]上的平均变化率
18.如图,直三棱柱ABC—A1B1C1中ACB=90o,M,N分别为A1B,B1C1的中点.求证:
(1)BC∥平面MNB1:
(2)平面A1CB上平面ACC1A1.
19.在四棱锥中,底面是矩形,平 面,,. 以的中点为球心、为直径的球面交于点,交于点.
(1)求证:平面⊥平面;
(2)求直线与平面所成的角的大小;
(3)求点到平面的距离.
20.体育教师选取某组10名大学生进行100米短跑和5 000米长跑两项运动水平的测试(如下表).
学生编号
1
2
3
4
5
6
7
8
9
10
短跑名次(x)
6
7
3
8
1
9
2
10
4
5
长跑名次(y)
7
10
2
5
4
8
3
9
1
6
(1)画出散点图
(2)求y与x的回归直线方程
21.已知函数.
(Ⅰ)若,求曲线在点处的切线方程;
(Ⅱ)若且函数在其定义域内为增函数,求实数的取值范围;
(Ⅲ)若函数在存在极值,求实数的取值范围.
22.写出下列命题的否定与否命题:
(1)等腰三角形有两个内角相等.
(2)可以被5整除的整数,末位是0.
(3)若xy=0,则x=0或y=0.
参考答案
一、选择题
1.C??????2.A??????
解析:如图所示, 设=,=,+=,则,= P(1, ),Q(k, k2 ), =(1,0), =(,), =(+1, ),则直线OG的方程为 y=x=,解得2 =1-, ||=1, 1-0,k2
3.A??????4.B??????
解析:
5.C??????6.A??????
解析:
7.C??????
解析:连接AC、BD交于O,连接OE,因OE∥SD.所以∠AEO为所求。设侧棱长与底面边长都等于2,则在⊿AEO中,OE=1,AO=,AE=, 于是
8.B??????9.D??????
解析:直线OA的方程是y=xcos,即xcos-y=0,点B到直线OA的距离d==,|OA|=,故 ? △OAB的面积|OA|·d= (1-sincos)=(1一sin2)[,].选D
10.C??????
解析:①③④正确,②错误.易求得、到球心的距离分别为3、2,若两弦交于,则⊥,中,有,矛盾。当、、共线时分别取最大值5最小值1.
11.A??????12.A??????
解析:∥,m,n.可能有m∥n,也可能有m与n异面,故②错;m∥n,m∥,则可能有n∥,也可能有n,故③错;易知①④正确,故选A
二、填空题
13.
14.
15.
16.
三、解答题
17.a
18.解:(1)因为BC∥B1 C1 ,且B1 C1 平面MNB1 ,BC平面MNB1 ,故BC∥平面MNB1 (2)因为BCAC,且ABC—A1 B1 C1 为直三棱柱, 故BC平面ACC1 A1 因为BC平面A1 CB, 故平面A1 CB平面ACC1 A1
19.方法一: ????? (1)依题设知,是所作球面的直径,则. ?????? 又因为平面,则,又, ?????? 所以平面,则,所以平面, ?????? 所以平面平面. ????? (2)由(1)知,,又,则是的中点 ?????? 可得, ?????? 则 ?????? 设到平面的距离为,由即, ?????? 可求得, ?????? 设所求角为,则,. ????? (3)可求得.因为,由,得.所以:????????? ?????? =:. ?????? 故点到平面的距离等于点到平面距离的. ?????? 又因为是的中点,则、到平面的距离相等,由(2)可知所求????????????? ?????? 距离为. ?? 方法二: (1)同方法一; (2)如图所示,建立空间直角坐标系,则,,,,,;设平面的一个法向量,由可得:,令,则.设所求角为,则,所以所求角的大小为. (3)由条件可得,在中,,所以,则,,所以所求距离等于点到平面距离的,设点到平面距离为则,所以所求距离为.
20.(1)略 (2)=0.745x+1.4
21. ????????????? (Ⅱ), ????????????? 要使在定义域内是增函数,只需在内恒成立 ????????????? 即在上恒成立, ????????????? (法一)即在上恒成立 ????????????? ∴,设 ????????????? 则 ????????????? ∵,∴ ,当且仅当时取等号 ????????????? ∴ ,即,∴ ????????????? 所以实数的取值范围是 (法二)令, 要使在定义域内是增函数,只需在内恒成立. 由题意,的图象为开口向上的抛物线, 对称轴方程为,∴, ∴, 解得 ∴实数的取值范围是.(Ⅲ)∵,令,即 设 当时,方程()的解为,此时在无极值, 所以; 当时,的对称轴方程为 ①若在恰好有一个极值 则 ,解得 ????????????? 此时在存在一个极大值;????????????? ????????????? ②若在恰好两个极值,即在有两个不等实根 ????????????? 则 或 ,解得????????????? ????????????? . ????????????? 综上所述,当时,在存在极值.
22.(1)命题的否定:存在一个等腰三角形,没有两个内角相等.否命题:若三角形不是等腰三角形,则它的任意两个内角都不相等. (2)命题的否定:存在一个可以被5整除的整数,其末位不是0.否命题:不能被5整除的整数,其末位不是0. (3)命题的否定:若xy=0,则x≠0且y≠0.否命题:若xy≠0,则x≠0且y≠0.
同课章节目录
