北师大版六年级下册1.1面的旋转同步练习(含答案)
文档属性
| 名称 | 北师大版六年级下册1.1面的旋转同步练习(含答案) | 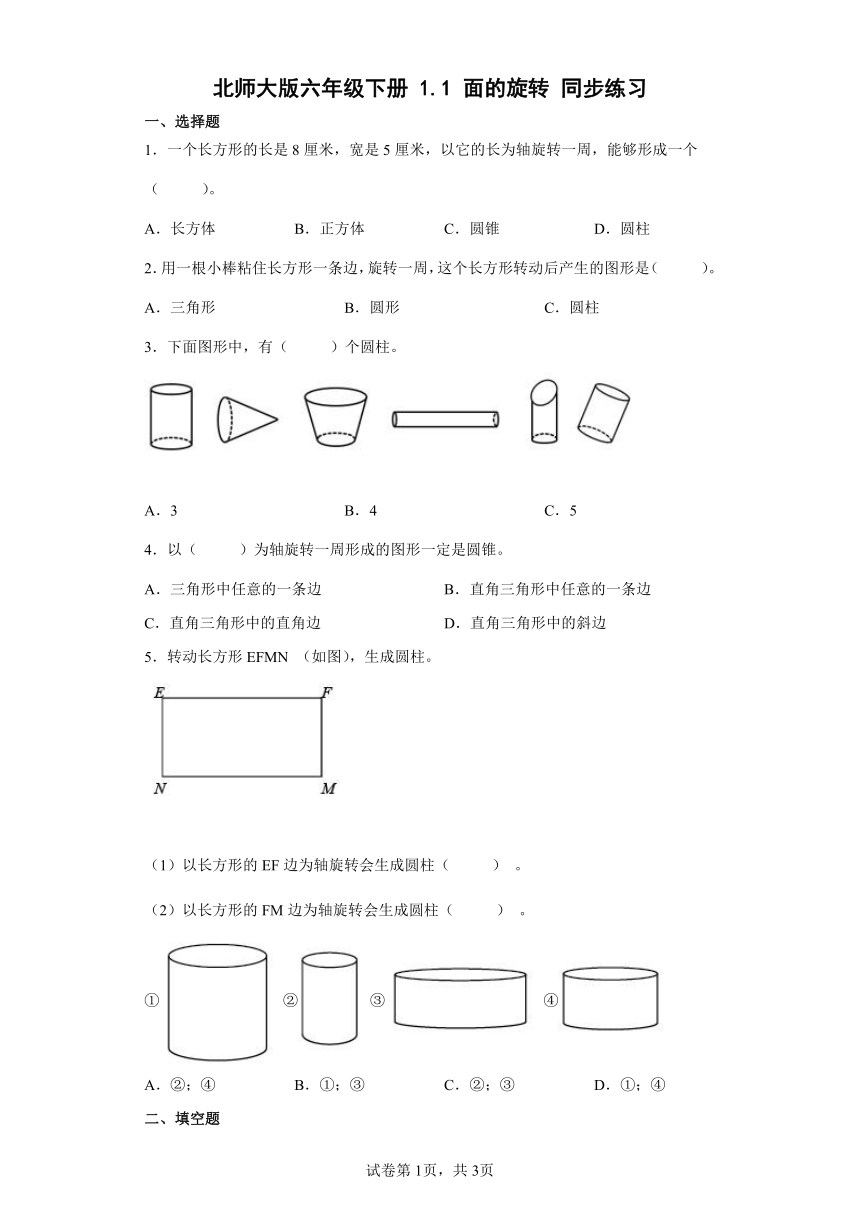 | |
| 格式 | docx | ||
| 文件大小 | 69.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 11:53:44 | ||
图片预览



文档简介
北师大版六年级下册 1.1 面的旋转 同步练习
一、选择题
1.一个长方形的长是8厘米,宽是5厘米,以它的长为轴旋转一周,能够形成一个( )。
A.长方体 B.正方体 C.圆锥 D.圆柱
2.用一根小棒粘住长方形一条边,旋转一周,这个长方形转动后产生的图形是( )。
A.三角形 B.圆形 C.圆柱
3.下面图形中,有( )个圆柱。
A.3 B.4 C.5
4.以( )为轴旋转一周形成的图形一定是圆锥。
A.三角形中任意的一条边 B.直角三角形中任意的一条边
C.直角三角形中的直角边 D.直角三角形中的斜边
5.转动长方形EFMN (如图),生成圆柱。
(1)以长方形的EF边为轴旋转会生成圆柱( ) 。
(2)以长方形的FM边为轴旋转会生成圆柱( ) 。
① ② ③ ④
A.②;④ B.①;③ C.②;③ D.①;④
二、填空题
6.长方形沿一条长旋转一周后形成一个_____,直角三角形沿着一条直角边旋转之后形成一个_____.
7.以一个长8厘米,宽6厘米的长方形的长为轴旋转一周,得到一个( ),底面直径是( )厘米,高是( )厘米。
8.将直角三角形以一条直角边为轴按图示的方向旋转一周,得到的图形是( ),它的底面积是( )。
9.把一个直角三角形沿一条直角边为轴旋转,会得到一个( )。圆锥只有( )底面,是一个( )。圆锥的侧面是一个( )。从圆锥顶点到( )的距离是圆锥的高。
三、判断题
10.以直角三角形的最长边为轴旋转360度,会形成一个圆锥。( )
11.一个长方形绕一条长边旋转一周所形成的图形是圆柱。( )
12.以三角形的一条边为轴旋转一周一定可以得到一个圆锥体. ( )
13.一个矩形绕着其中一条边旋转360°,能得到一个圆柱;一个三角形绕着其中一条边旋转360°,也能得到一个圆锥.( )
14.圆柱可以由长方形绕一条边旋转形成,圆锥可以由直角三角形绕一条直角边旋转形成. ( )
四、解答题
15.转动长方形ABCD。形成右边的两个圆柱,说一说它们分别是以长方形的哪条边为轴旋转形成的?底面半径和高分别是多少?
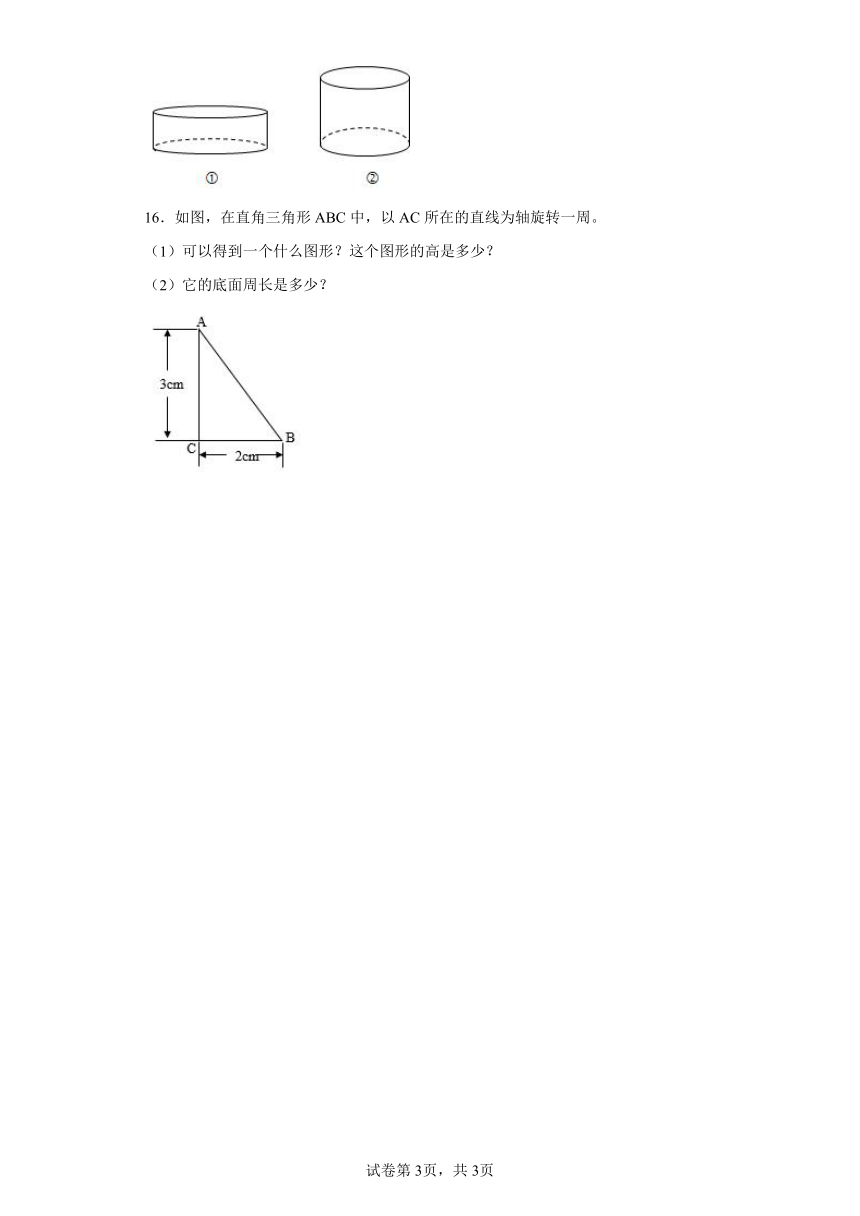
16.如图,在直角三角形ABC中,以AC所在的直线为轴旋转一周。
(1)可以得到一个什么图形?这个图形的高是多少?
(2)它的底面周长是多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
一个长方形的长是8厘米,宽是5厘米,以它的长为轴旋转一周,能够形成一个圆柱,其中圆柱的底面半径是5厘米,高是8厘米,据此解答。
【详解】
由分析可知,一个长方形以它的长为轴旋转一周,能够形成一个圆柱。
故选择:D
【点睛】
此题考查了圆柱的认识,属于基础类题目。
2.C
【解析】
根据圆柱的特征判断即可。
【详解】
用一根小棒粘住长方形一条边,旋转一周,这个长方形转动后产生的图形是圆柱,粘住小棒的一边为圆柱的高,相邻的另一条边为圆柱的底面半径。
故答案为:C。
【点睛】
本题考查圆柱的特征,解答本题的关键是掌握圆柱的特征。
3.A
【解析】
【分析】
圆柱的特征:
(1)圆柱上下两个底面是相等的两个圆。
(2)圆柱有无数条高。
(3)同一个圆柱两底面间的距离处处相等。
据此解答。
【详解】
根据圆柱的特征可知,第1个、第4个、第6个图形是圆柱,一共有3个圆柱。
故答案为:A
【点睛】
根据圆柱的特征即可解答。
4.C
【解析】
【分析】
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥,据此解答。
【详解】
根据分析可知,直角三角形中的直角边轴,旋转一周形成的圆形一定是圆锥。
故答案选:C
【点睛】
本题考查圆锥的特点,根据圆锥的特点进行解答。
5.B
【解析】
【分析】
圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。
【详解】
(1)以长方形的EF边为轴旋转会生成圆柱 。
(2)以长方形的FM边为轴旋转会生成圆柱 。
故答案为:B
【点睛】
关键是熟悉圆柱特征,具有一定的空间想象能力。
6. 圆柱 圆锥
【解析】
【详解】
略
7. 圆柱 12 8
【解析】
【分析】
由题意知:一个长8厘米,宽6厘米的长方形,以长为轴旋转一周,得到一个底面直径是两个宽的和12厘米,高是长方形的长8厘米的圆柱。据此解答。
【详解】
从一个长8厘米,宽6厘米的长方形的长为轴旋转一周,得到一个圆柱,底面直径是12厘米,高是8厘米。
【点睛】
抓住圆柱的特征,即可找出对应的数据。
8. 圆锥 28.26
【解析】
【分析】
由题意知:将直角三角形以一条直角边为轴按图示的方向旋转一周,得到的图形是一个圆锥。底面是一个半径为3厘米的圆,用圆的面积公式计算即可得底面积。
【详解】
如图,
将直角三角形以一条直角边为轴按图示的方向旋转一周,得到的图形是圆锥;
。
【点睛】
掌握圆锥的特征是解答本题的关键。
9. 圆锥 一个 圆形 曲面 底面圆心
【解析】
【详解】
如下图:
由图可知:把一个直角三角形沿一条直角边为轴旋转,会得到一个圆锥。圆锥只有一个底面,是一个圆形。圆锥的侧面是一个曲面。从圆锥顶点到底面圆心的距离是圆锥的高。
10.×
【解析】
【分析】
以直角三角形的一条直角边为旋转轴旋转可得到一个圆锥,若以直角三角形的斜边为旋转轴旋转一周则会得到一个两个等底圆锥拼成的纺锤体;据此解答。
【详解】
由分析可得:以直角三角形的最长边为轴旋转360度,会形成一个两个等底圆锥拼成的纺锤体。
故答案为:×
【点睛】
解答此题的关键确定旋转图形的旋转轴,然后再确定旋转后得到的物体。
11.√
【解析】
【分析】
根据圆柱的意义,以长方形的一边为旋转轴,其余三边旋转形成的面围成的旋转体叫做圆柱,所以一个长方形绕着长为轴旋转一周,可以得到一个圆柱体,据此解答即可。
【详解】
圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。由此可知:一个长方形绕它的一条长旋转一周后得到的图形是圆柱。
故判断正确。
【点睛】
一个长方形绕着其中一边旋转一周,可以得到一个圆柱体。
12.错误
【解析】
【详解】
略
13.错误
【解析】
【分析】
一个矩形绕着其中一条边旋转360°,能得到一个圆柱;一个直角三角形绕着其中一条直角边旋转360°,能得到一个圆锥;一个不是直角三角形的三角形绕着其中一条边旋转360°,能得到两个圆锥.
【详解】
一个矩形绕着其中一条边旋转360°,能得到一个圆柱;一个直角三角形绕着其中一条直角边旋转360°,能得到一个圆锥.
故答案为错误.
14.√
【解析】
【详解】
略
15.圆柱①是长方形ABCD以AB或CD边为轴旋转一周得到的,底面半径为1厘米,圆柱高为0.5厘米。
圆柱②是长方形ABCD以AD或BC边为轴旋转一周得到的,底面半径为0.5厘米,圆柱高为1厘米。
【解析】
【分析】
根据面动成体,转动长方形ABCD,以AB或CD边为轴旋转一周,得到的圆柱高为0.5厘米,底面半径为1厘米,生成圆柱①;以AD或BC为轴旋转一周得到的圆柱高为1厘米,底面半径为0.5厘米,生成圆柱②。
【详解】
圆柱①是长方形ABCD以AB或CD边为轴旋转一周得到的,底面半径为1厘米,圆柱高为0.5厘米;
圆柱②是长方形ABCD以AD或BC边为轴旋转一周得到的,底面半径为0.5厘米,圆柱高为1厘米。
【点睛】
一个长方形绕长(或宽)为旋转轴转动一周,将得到一个以长(或宽)为高宽(或长)为底面半径的圆柱。
16.(1)可以得到一个圆锥,这个图形的高是3cm。
(2)12.56厘米
【解析】
【分析】
(1)直角三角形ABC中,以AC所在的直线为轴旋转一周,可以得到一个圆锥,这个图形的高是原三角形的高,即3cm;
(2)圆锥的底面是个圆,底面半径是原三角形的底,是2cm,根据圆的周长公式:周长=2×半径×π,所以底面周长是2×2×3.14=12.56厘米,即可解答。
【详解】
(1)可以得到一个圆锥,这个图形的高是3cm。
(2)2×2×3.14
=4×3.14
=12.56(cm)
答:它的底面周长是12.56厘米。
【点评】
解答此题的关键是掌握圆锥的特征和面动成体的规律。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.一个长方形的长是8厘米,宽是5厘米,以它的长为轴旋转一周,能够形成一个( )。
A.长方体 B.正方体 C.圆锥 D.圆柱
2.用一根小棒粘住长方形一条边,旋转一周,这个长方形转动后产生的图形是( )。
A.三角形 B.圆形 C.圆柱
3.下面图形中,有( )个圆柱。
A.3 B.4 C.5
4.以( )为轴旋转一周形成的图形一定是圆锥。
A.三角形中任意的一条边 B.直角三角形中任意的一条边
C.直角三角形中的直角边 D.直角三角形中的斜边
5.转动长方形EFMN (如图),生成圆柱。
(1)以长方形的EF边为轴旋转会生成圆柱( ) 。
(2)以长方形的FM边为轴旋转会生成圆柱( ) 。
① ② ③ ④
A.②;④ B.①;③ C.②;③ D.①;④
二、填空题
6.长方形沿一条长旋转一周后形成一个_____,直角三角形沿着一条直角边旋转之后形成一个_____.
7.以一个长8厘米,宽6厘米的长方形的长为轴旋转一周,得到一个( ),底面直径是( )厘米,高是( )厘米。
8.将直角三角形以一条直角边为轴按图示的方向旋转一周,得到的图形是( ),它的底面积是( )。
9.把一个直角三角形沿一条直角边为轴旋转,会得到一个( )。圆锥只有( )底面,是一个( )。圆锥的侧面是一个( )。从圆锥顶点到( )的距离是圆锥的高。
三、判断题
10.以直角三角形的最长边为轴旋转360度,会形成一个圆锥。( )
11.一个长方形绕一条长边旋转一周所形成的图形是圆柱。( )
12.以三角形的一条边为轴旋转一周一定可以得到一个圆锥体. ( )
13.一个矩形绕着其中一条边旋转360°,能得到一个圆柱;一个三角形绕着其中一条边旋转360°,也能得到一个圆锥.( )
14.圆柱可以由长方形绕一条边旋转形成,圆锥可以由直角三角形绕一条直角边旋转形成. ( )
四、解答题
15.转动长方形ABCD。形成右边的两个圆柱,说一说它们分别是以长方形的哪条边为轴旋转形成的?底面半径和高分别是多少?
16.如图,在直角三角形ABC中,以AC所在的直线为轴旋转一周。
(1)可以得到一个什么图形?这个图形的高是多少?
(2)它的底面周长是多少?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
一个长方形的长是8厘米,宽是5厘米,以它的长为轴旋转一周,能够形成一个圆柱,其中圆柱的底面半径是5厘米,高是8厘米,据此解答。
【详解】
由分析可知,一个长方形以它的长为轴旋转一周,能够形成一个圆柱。
故选择:D
【点睛】
此题考查了圆柱的认识,属于基础类题目。
2.C
【解析】
根据圆柱的特征判断即可。
【详解】
用一根小棒粘住长方形一条边,旋转一周,这个长方形转动后产生的图形是圆柱,粘住小棒的一边为圆柱的高,相邻的另一条边为圆柱的底面半径。
故答案为:C。
【点睛】
本题考查圆柱的特征,解答本题的关键是掌握圆柱的特征。
3.A
【解析】
【分析】
圆柱的特征:
(1)圆柱上下两个底面是相等的两个圆。
(2)圆柱有无数条高。
(3)同一个圆柱两底面间的距离处处相等。
据此解答。
【详解】
根据圆柱的特征可知,第1个、第4个、第6个图形是圆柱,一共有3个圆柱。
故答案为:A
【点睛】
根据圆柱的特征即可解答。
4.C
【解析】
【分析】
以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥,据此解答。
【详解】
根据分析可知,直角三角形中的直角边轴,旋转一周形成的圆形一定是圆锥。
故答案选:C
【点睛】
本题考查圆锥的特点,根据圆锥的特点进行解答。
5.B
【解析】
【分析】
圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。
【详解】
(1)以长方形的EF边为轴旋转会生成圆柱 。
(2)以长方形的FM边为轴旋转会生成圆柱 。
故答案为:B
【点睛】
关键是熟悉圆柱特征,具有一定的空间想象能力。
6. 圆柱 圆锥
【解析】
【详解】
略
7. 圆柱 12 8
【解析】
【分析】
由题意知:一个长8厘米,宽6厘米的长方形,以长为轴旋转一周,得到一个底面直径是两个宽的和12厘米,高是长方形的长8厘米的圆柱。据此解答。
【详解】
从一个长8厘米,宽6厘米的长方形的长为轴旋转一周,得到一个圆柱,底面直径是12厘米,高是8厘米。
【点睛】
抓住圆柱的特征,即可找出对应的数据。
8. 圆锥 28.26
【解析】
【分析】
由题意知:将直角三角形以一条直角边为轴按图示的方向旋转一周,得到的图形是一个圆锥。底面是一个半径为3厘米的圆,用圆的面积公式计算即可得底面积。
【详解】
如图,
将直角三角形以一条直角边为轴按图示的方向旋转一周,得到的图形是圆锥;
。
【点睛】
掌握圆锥的特征是解答本题的关键。
9. 圆锥 一个 圆形 曲面 底面圆心
【解析】
【详解】
如下图:
由图可知:把一个直角三角形沿一条直角边为轴旋转,会得到一个圆锥。圆锥只有一个底面,是一个圆形。圆锥的侧面是一个曲面。从圆锥顶点到底面圆心的距离是圆锥的高。
10.×
【解析】
【分析】
以直角三角形的一条直角边为旋转轴旋转可得到一个圆锥,若以直角三角形的斜边为旋转轴旋转一周则会得到一个两个等底圆锥拼成的纺锤体;据此解答。
【详解】
由分析可得:以直角三角形的最长边为轴旋转360度,会形成一个两个等底圆锥拼成的纺锤体。
故答案为:×
【点睛】
解答此题的关键确定旋转图形的旋转轴,然后再确定旋转后得到的物体。
11.√
【解析】
【分析】
根据圆柱的意义,以长方形的一边为旋转轴,其余三边旋转形成的面围成的旋转体叫做圆柱,所以一个长方形绕着长为轴旋转一周,可以得到一个圆柱体,据此解答即可。
【详解】
圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。由此可知:一个长方形绕它的一条长旋转一周后得到的图形是圆柱。
故判断正确。
【点睛】
一个长方形绕着其中一边旋转一周,可以得到一个圆柱体。
12.错误
【解析】
【详解】
略
13.错误
【解析】
【分析】
一个矩形绕着其中一条边旋转360°,能得到一个圆柱;一个直角三角形绕着其中一条直角边旋转360°,能得到一个圆锥;一个不是直角三角形的三角形绕着其中一条边旋转360°,能得到两个圆锥.
【详解】
一个矩形绕着其中一条边旋转360°,能得到一个圆柱;一个直角三角形绕着其中一条直角边旋转360°,能得到一个圆锥.
故答案为错误.
14.√
【解析】
【详解】
略
15.圆柱①是长方形ABCD以AB或CD边为轴旋转一周得到的,底面半径为1厘米,圆柱高为0.5厘米。
圆柱②是长方形ABCD以AD或BC边为轴旋转一周得到的,底面半径为0.5厘米,圆柱高为1厘米。
【解析】
【分析】
根据面动成体,转动长方形ABCD,以AB或CD边为轴旋转一周,得到的圆柱高为0.5厘米,底面半径为1厘米,生成圆柱①;以AD或BC为轴旋转一周得到的圆柱高为1厘米,底面半径为0.5厘米,生成圆柱②。
【详解】
圆柱①是长方形ABCD以AB或CD边为轴旋转一周得到的,底面半径为1厘米,圆柱高为0.5厘米;
圆柱②是长方形ABCD以AD或BC边为轴旋转一周得到的,底面半径为0.5厘米,圆柱高为1厘米。
【点睛】
一个长方形绕长(或宽)为旋转轴转动一周,将得到一个以长(或宽)为高宽(或长)为底面半径的圆柱。
16.(1)可以得到一个圆锥,这个图形的高是3cm。
(2)12.56厘米
【解析】
【分析】
(1)直角三角形ABC中,以AC所在的直线为轴旋转一周,可以得到一个圆锥,这个图形的高是原三角形的高,即3cm;
(2)圆锥的底面是个圆,底面半径是原三角形的底,是2cm,根据圆的周长公式:周长=2×半径×π,所以底面周长是2×2×3.14=12.56厘米,即可解答。
【详解】
(1)可以得到一个圆锥,这个图形的高是3cm。
(2)2×2×3.14
=4×3.14
=12.56(cm)
答:它的底面周长是12.56厘米。
【点评】
解答此题的关键是掌握圆锥的特征和面动成体的规律。
答案第1页,共2页
答案第1页,共2页
