北师大版六年级下册1.4圆锥的体积同步练习
文档属性
| 名称 | 北师大版六年级下册1.4圆锥的体积同步练习 | 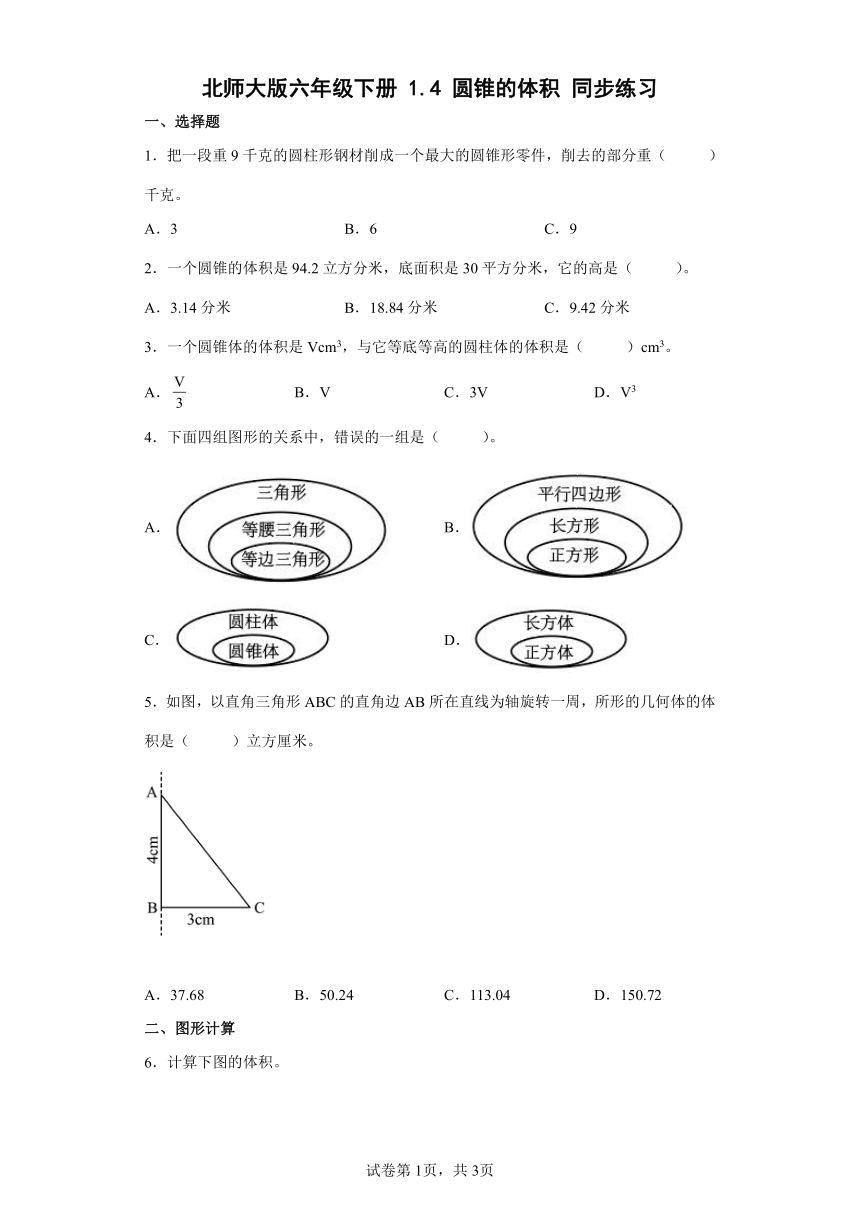 | |
| 格式 | docx | ||
| 文件大小 | 124.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 11:59:56 | ||
图片预览





文档简介
北师大版六年级下册 1.4 圆锥的体积 同步练习
一、选择题
1.把一段重9千克的圆柱形钢材削成一个最大的圆锥形零件,削去的部分重( )千克。
A.3 B.6 C.9
2.一个圆锥的体积是94.2立方分米,底面积是30平方分米,它的高是( )。
A.3.14分米 B.18.84分米 C.9.42分米
3.一个圆锥体的体积是Vcm3,与它等底等高的圆柱体的体积是( )cm3。
A. B.V C.3V D.V3
4.下面四组图形的关系中,错误的一组是( )。
A. B.
C. D.
5.如图,以直角三角形ABC的直角边AB所在直线为轴旋转一周,所形的几何体的体积是( )立方厘米。
A.37.68 B.50.24 C.113.04 D.150.72
二、图形计算
6.计算下图的体积。
7.求下面立体图形的体积。(单位:cm)
三、填空题
8.圆柱和圆锥的底面积、体积分别相等,圆锥的高是15厘米,圆柱的高是( )厘米。
9.一个圆锥的底面积是一个长方体底面积的,它们的高相等,那么这个圆锥的体积是长方体体积的( )。
A. B. C.
10.把一个底面直径是4dm,高是6dm的圆柱形木料削成一个最大的圆锥,削去部分的体积是( )dm3,削成圆锥的体积是( )dm3。
11.下面的直角梯形的两个底分别是6cm和9cm,高是2cm,以较长的底为轴旋转一周,得到的几何体的体积是( )cm3。
四、判断题
12.圆柱的体积是圆锥的体积的三倍。( )
13.底面积与高一样的圆锥和圆柱体积比为1∶2。( )
14.一个圆锥的底面半径和高相等,过顶点和直径把这个圆锥切开,切面一定是等腰直角三角形。( )
15.圆锥圆柱的体积都等于它们的底面积乘以高。( )
16.一个圆柱和一个圆锥的体积相等,那么这个圆锥和圆柱一定等底等高。( )
五、解答题
17.把一个底面半径为6厘米的圆锥体铁块放入一个底面半径10厘米,高30厘米的圆柱形容器里,完全浸入到水中,水面上升了3厘米,求这个圆锥体铁块的高是几厘米?
18.沿着虚线将下面图形旋转一周, 旋转后的立体图形的体积是多少?
19.图中所示图形是一个底面直径为30厘米的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为8厘米,高12厘米的一个圆锥体铅锤,水面刚好盖住铅锤,当铅锤从水中取出后,杯里的水将下降几厘米?(π=3.14结果保留两位小数)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
圆柱内最大的圆锥的体积是圆柱的体积的,则削去部分就是圆柱的体积的,根据分数乘法的意义即可求出削去的部分的钢的重量。
【详解】
9×(1-)
=9×
=6(千克)
削去的部分重6千克。
故答案选:B
【点睛】
抓住圆柱内最大的圆锥的体积是圆柱的体积的,是解决此类问题的关键。
2.C
【解析】
【分析】
由圆锥的体积=×底面积×高可知:圆锥的高=体积×3÷底面积,代入数据计算即可。
【详解】
94.2×3÷30
=282.6÷30
=9.42(分米)
故答案为:C
【点睛】
本题主要考查圆锥体积公式的灵活运用。
3.C
【解析】
【分析】
等底等高的圆柱的体积是圆锥体积的3倍;据此解答。
【详解】
V×3=3V(cm3)
故答案为:C
【点睛】
熟记等底等高的圆锥与圆柱的体积之间的关系是解答此题的关键。
4.C
【解析】
【分析】
根据三角形、等腰三角形、等边三角形的特征关系,平行四边形、长方形、正方形的特征关系和正方体、长方体特征关系进行选择。
【详解】
A.等边三角形是特殊的等腰三角形,等边三角形和等腰三角形是特殊的三角形
B.正方形是特殊的长方形,长方形和正方形又是特殊的平行四边形
C.圆锥体不是特殊的圆柱体
D.正方体是特殊的长方体
选项C和其他三个选项表现的特征不一致
故答案为:C
【点睛】
本题考查几组平面图形的关系,把握它们之间的包含关系,明白哪个图形范围最大,哪个图形的范围最小。
5.A
【解析】
【分析】
根据题意可知,旋转得到的几何体为圆锥体,圆锥的底面半径为3厘米,高为4厘米,再根据“”求出圆锥的体积即可。
【详解】
3.14×3 ×4×
=28.26×4×
=37.68(立方厘米);
故答案为:A。
【点睛】
明确旋转后得到的圆锥体底面半径和高分别为多少是解答本题的关键。
6.10.8立方厘米
【解析】
【分析】
由图意知:这是一个圆锥体,底面积是9平方厘米,高是3.6厘米,利用圆锥的体积公式,将数值代入即可求得体积。
【详解】
(立方厘米)
7.15.7cm3
【解析】
【分析】
通过观察,该立体图形的体积=圆柱的体积+圆锥的体积,圆柱的体积为3.14×r2×h,圆锥的体积为×3.14×r2×h,将数据代入公式即可。
【详解】
3.14×(2÷2)2×4+×3.14×(2÷2)2×3
=3.14×1×4+3.14×1×1
=3.14×5
=15.7(cm3)
8.5
【解析】
【分析】
等体积等底面积的圆柱和圆锥,圆锥的高是圆柱的3倍,直接用圆锥的高÷3即可。
【详解】
15÷3=5(厘米)
【点睛】
关键是掌握圆柱和圆锥体积之间的关系,等底等高的圆柱和圆锥,圆柱的体积是圆锥的3倍;等体积等底面积的圆柱和圆锥,圆锥的高是圆柱的3倍。
9.C
【解析】
【分析】
根据题意,设圆锥的底面积为s,则长方体的底面积3s,圆锥的高为h,则长方体的高也为h,根据圆锥的体积公式:×底面积×高,长方体体积公式:底面积×高,用圆锥的体积除以长方体的体积,即可解答。
【详解】
设:圆锥的底面积为s,则长方体的底面为3s,圆锥的高为h,长方体的高为h;
圆锥的体积:sh
长方体的体积:3sh
sh∶3sh=×=
故答案选:C
【点睛】
本题考查圆锥的体积公式、长方体的体积公式的应用,熟记公式,灵活运用。
10. 50.24 25.12
【解析】
【分析】
把圆柱削成最大的圆锥,圆锥与圆柱的底面积和高都相等,则圆锥的体积是圆柱体积的 ,削去部分的体积等于圆柱体积的(1-),根据圆柱的体积V=πr2h,代入计算即可。
【详解】
3.14×(4÷2)2×6
=3.14×4×6
=3.14×24
=75.36(dm3);
削去部分体积:
75.36×(1-)
=75.36×
=50.24(dm3);
圆锥的体积:75.36×=25.12(dm3);
【点睛】
此题考查了圆柱与圆锥的体积关系,掌握公式认真计算即可。
11.87.92
【解析】
【分析】
旋转一周得到的图形可以看成是一个圆柱形加上上面一个圆锥就可以了;.圆锥半径为圆柱半径(即梯形高2cm),圆锥高度为两底边之差(即3cm),圆柱高度为上底底边6cm,V体积=V圆锥+V圆柱,V柱=πr2h V锥=πr2h;据此解答。
【详解】
3.14×22×6+×3.14×22×(9-6)
=3.14×24+3.14×4
=75.36+12.56
=87.92(立方厘米)
【点睛】
此题考查的是圆柱和圆锥的体积公式的运用,解答此题的关键是理解旋转一周得到的图形是一个圆柱形加上一个圆锥。
12.×
【解析】
【分析】
等底等高的圆柱的体积是圆锥的体积的三倍。
【详解】
根据分析可得,要使圆柱的体积是圆锥的体积的三倍,必须建立在二者等底等高的前提下,故本题说法错误。
故答案为:×。
【点睛】
本题考查圆柱、圆锥的体积,解答本题的关键是掌握圆柱、圆锥的体积之间的关系。
13.×
【解析】
【分析】
等底等高的圆锥和圆柱,圆柱的体积是圆锥体积的3倍,据此解答。
【详解】
设:圆锥的底面积为s,圆柱底面积也是s,圆锥的高是h,圆柱的高也是h
圆锥的体积是:sh
圆柱的体积是:sh
圆锥的体积∶圆柱的体积=sh∶sh
=
=1∶3
底面积与高一样的圆锥和圆柱体积比为1∶3;
原题干底面积与高一样的圆锥和圆柱体积比为1∶2,说法错误。
故答案为:×
【点睛】
本题考查等底等高圆锥与圆柱体积的关系,根据圆锥、圆柱的体积公式进行解答。
14.√
【解析】
【分析】
圆锥纵切面是一个三角形,三角形的底是圆锥底面直径,三角形高是圆锥的高,如果圆锥的底面半径和高相等,纵切面如图,切面是一个等腰直角三角形。
【详解】
根据分析,一个圆锥的底面半径和高相等,过顶点和直径把这个圆锥切开,切面一定是等腰直角三角形,说法正确。
故答案为:√
【点睛】
关键是熟悉圆锥特征,想清楚纵切面和圆锥之间的关系。
15.×
【解析】
【分析】
圆柱的体积=底面积×高,圆锥的体积=圆锥的体积=×底面积×高,据此解答。
【详解】
根据分析可知,圆锥圆柱的体积都等于它们的底面积乘以高,说法错误。
故答案为:×
【点睛】
考查了圆柱和圆锥的体积,学生应熟练掌握。
16.×
【解析】
【分析】
因为等底等高的圆锥的体积是圆柱体积的,可以通过举例证明。
【详解】
假设一个圆柱的底面积是12.56平方厘米,高是9厘米,体积是12.56×9=113.04(立方厘米),
如果圆锥的体积是113.04立方厘米,底面积是12.56平方厘米,
那么圆锥的高是:113.04÷÷12.56
=113.04×3÷12.56
=339.12÷12.56
=27(厘米);
因此,圆柱和圆锥的体积相等,它们的高不一定相等。
故答案为:×
【点睛】
理解掌握等底等高的圆锥的体积是圆柱体积的是解答关键。
17.25厘米
【解析】
【分析】
由题意可知:圆锥体铁块的体积就等于上升3厘米的水的体积,将数据带入圆柱的体积公式:V=sh=πr2h,求出高3厘米的水的体积(圆锥的体积),再根据圆锥的体积公式:V=sh=πr2h,求出圆锥的高即可。
【详解】
3.14×102×3÷÷(3.14×62)
=3.14×102×3×3÷3.14÷62
=900÷36
=25(厘米)
答:这个圆锥体铁块的高是25厘米。
【点睛】
本题主要考查体积的等积变形,灵活运用圆柱、圆锥的体积公式是解题的关键。
18.197.82立方分米
【解析】
【分析】
将下图沿着虚线旋转一周,得到的立体图形是一个圆锥和一个圆柱组合而成,根据根据圆柱的体积公式:V=Sh(圆柱的高);圆锥的体积公式:V=Sh(圆锥的高),把数代入即可求解。
【详解】
圆锥的体积:3.14×3×3×3×
=9.42×3×3×
=28.26(立方分米)
圆柱的体积:3.14×3×3×6
=28.26×6
=169.56(立方分米)
169.56+28.26=197.82(立方分米)
答:旋转后的立体图形的体积是197.82立方分米。
【点睛】
本题主要考查圆柱和圆锥的体积公式,熟练掌握它们的体积公式并灵活运用。
19.0.28厘米
【解析】
【分析】
根据圆锥的体积公式:V=πr2h,求出圆锥体铅锤的体积,用圆锥体铅锤的体积除以圆柱形玻璃杯的底面积即可。
【详解】
3.14×(8÷2)2×12×÷[3.14×(30÷2)2]
=3.14×16×12×÷[3.14×225]
=50.24×12×÷706.5
=602.88×÷706.5
=200.96÷706.5
≈0.28(厘米)
答:杯里的水下降0.28厘米。
【点睛】
此题主要考查圆锥体积公式和圆柱体的体积公式的灵活运用,关键是熟记公式。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.把一段重9千克的圆柱形钢材削成一个最大的圆锥形零件,削去的部分重( )千克。
A.3 B.6 C.9
2.一个圆锥的体积是94.2立方分米,底面积是30平方分米,它的高是( )。
A.3.14分米 B.18.84分米 C.9.42分米
3.一个圆锥体的体积是Vcm3,与它等底等高的圆柱体的体积是( )cm3。
A. B.V C.3V D.V3
4.下面四组图形的关系中,错误的一组是( )。
A. B.
C. D.
5.如图,以直角三角形ABC的直角边AB所在直线为轴旋转一周,所形的几何体的体积是( )立方厘米。
A.37.68 B.50.24 C.113.04 D.150.72
二、图形计算
6.计算下图的体积。
7.求下面立体图形的体积。(单位:cm)
三、填空题
8.圆柱和圆锥的底面积、体积分别相等,圆锥的高是15厘米,圆柱的高是( )厘米。
9.一个圆锥的底面积是一个长方体底面积的,它们的高相等,那么这个圆锥的体积是长方体体积的( )。
A. B. C.
10.把一个底面直径是4dm,高是6dm的圆柱形木料削成一个最大的圆锥,削去部分的体积是( )dm3,削成圆锥的体积是( )dm3。
11.下面的直角梯形的两个底分别是6cm和9cm,高是2cm,以较长的底为轴旋转一周,得到的几何体的体积是( )cm3。
四、判断题
12.圆柱的体积是圆锥的体积的三倍。( )
13.底面积与高一样的圆锥和圆柱体积比为1∶2。( )
14.一个圆锥的底面半径和高相等,过顶点和直径把这个圆锥切开,切面一定是等腰直角三角形。( )
15.圆锥圆柱的体积都等于它们的底面积乘以高。( )
16.一个圆柱和一个圆锥的体积相等,那么这个圆锥和圆柱一定等底等高。( )
五、解答题
17.把一个底面半径为6厘米的圆锥体铁块放入一个底面半径10厘米,高30厘米的圆柱形容器里,完全浸入到水中,水面上升了3厘米,求这个圆锥体铁块的高是几厘米?
18.沿着虚线将下面图形旋转一周, 旋转后的立体图形的体积是多少?
19.图中所示图形是一个底面直径为30厘米的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为8厘米,高12厘米的一个圆锥体铅锤,水面刚好盖住铅锤,当铅锤从水中取出后,杯里的水将下降几厘米?(π=3.14结果保留两位小数)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
圆柱内最大的圆锥的体积是圆柱的体积的,则削去部分就是圆柱的体积的,根据分数乘法的意义即可求出削去的部分的钢的重量。
【详解】
9×(1-)
=9×
=6(千克)
削去的部分重6千克。
故答案选:B
【点睛】
抓住圆柱内最大的圆锥的体积是圆柱的体积的,是解决此类问题的关键。
2.C
【解析】
【分析】
由圆锥的体积=×底面积×高可知:圆锥的高=体积×3÷底面积,代入数据计算即可。
【详解】
94.2×3÷30
=282.6÷30
=9.42(分米)
故答案为:C
【点睛】
本题主要考查圆锥体积公式的灵活运用。
3.C
【解析】
【分析】
等底等高的圆柱的体积是圆锥体积的3倍;据此解答。
【详解】
V×3=3V(cm3)
故答案为:C
【点睛】
熟记等底等高的圆锥与圆柱的体积之间的关系是解答此题的关键。
4.C
【解析】
【分析】
根据三角形、等腰三角形、等边三角形的特征关系,平行四边形、长方形、正方形的特征关系和正方体、长方体特征关系进行选择。
【详解】
A.等边三角形是特殊的等腰三角形,等边三角形和等腰三角形是特殊的三角形
B.正方形是特殊的长方形,长方形和正方形又是特殊的平行四边形
C.圆锥体不是特殊的圆柱体
D.正方体是特殊的长方体
选项C和其他三个选项表现的特征不一致
故答案为:C
【点睛】
本题考查几组平面图形的关系,把握它们之间的包含关系,明白哪个图形范围最大,哪个图形的范围最小。
5.A
【解析】
【分析】
根据题意可知,旋转得到的几何体为圆锥体,圆锥的底面半径为3厘米,高为4厘米,再根据“”求出圆锥的体积即可。
【详解】
3.14×3 ×4×
=28.26×4×
=37.68(立方厘米);
故答案为:A。
【点睛】
明确旋转后得到的圆锥体底面半径和高分别为多少是解答本题的关键。
6.10.8立方厘米
【解析】
【分析】
由图意知:这是一个圆锥体,底面积是9平方厘米,高是3.6厘米,利用圆锥的体积公式,将数值代入即可求得体积。
【详解】
(立方厘米)
7.15.7cm3
【解析】
【分析】
通过观察,该立体图形的体积=圆柱的体积+圆锥的体积,圆柱的体积为3.14×r2×h,圆锥的体积为×3.14×r2×h,将数据代入公式即可。
【详解】
3.14×(2÷2)2×4+×3.14×(2÷2)2×3
=3.14×1×4+3.14×1×1
=3.14×5
=15.7(cm3)
8.5
【解析】
【分析】
等体积等底面积的圆柱和圆锥,圆锥的高是圆柱的3倍,直接用圆锥的高÷3即可。
【详解】
15÷3=5(厘米)
【点睛】
关键是掌握圆柱和圆锥体积之间的关系,等底等高的圆柱和圆锥,圆柱的体积是圆锥的3倍;等体积等底面积的圆柱和圆锥,圆锥的高是圆柱的3倍。
9.C
【解析】
【分析】
根据题意,设圆锥的底面积为s,则长方体的底面积3s,圆锥的高为h,则长方体的高也为h,根据圆锥的体积公式:×底面积×高,长方体体积公式:底面积×高,用圆锥的体积除以长方体的体积,即可解答。
【详解】
设:圆锥的底面积为s,则长方体的底面为3s,圆锥的高为h,长方体的高为h;
圆锥的体积:sh
长方体的体积:3sh
sh∶3sh=×=
故答案选:C
【点睛】
本题考查圆锥的体积公式、长方体的体积公式的应用,熟记公式,灵活运用。
10. 50.24 25.12
【解析】
【分析】
把圆柱削成最大的圆锥,圆锥与圆柱的底面积和高都相等,则圆锥的体积是圆柱体积的 ,削去部分的体积等于圆柱体积的(1-),根据圆柱的体积V=πr2h,代入计算即可。
【详解】
3.14×(4÷2)2×6
=3.14×4×6
=3.14×24
=75.36(dm3);
削去部分体积:
75.36×(1-)
=75.36×
=50.24(dm3);
圆锥的体积:75.36×=25.12(dm3);
【点睛】
此题考查了圆柱与圆锥的体积关系,掌握公式认真计算即可。
11.87.92
【解析】
【分析】
旋转一周得到的图形可以看成是一个圆柱形加上上面一个圆锥就可以了;.圆锥半径为圆柱半径(即梯形高2cm),圆锥高度为两底边之差(即3cm),圆柱高度为上底底边6cm,V体积=V圆锥+V圆柱,V柱=πr2h V锥=πr2h;据此解答。
【详解】
3.14×22×6+×3.14×22×(9-6)
=3.14×24+3.14×4
=75.36+12.56
=87.92(立方厘米)
【点睛】
此题考查的是圆柱和圆锥的体积公式的运用,解答此题的关键是理解旋转一周得到的图形是一个圆柱形加上一个圆锥。
12.×
【解析】
【分析】
等底等高的圆柱的体积是圆锥的体积的三倍。
【详解】
根据分析可得,要使圆柱的体积是圆锥的体积的三倍,必须建立在二者等底等高的前提下,故本题说法错误。
故答案为:×。
【点睛】
本题考查圆柱、圆锥的体积,解答本题的关键是掌握圆柱、圆锥的体积之间的关系。
13.×
【解析】
【分析】
等底等高的圆锥和圆柱,圆柱的体积是圆锥体积的3倍,据此解答。
【详解】
设:圆锥的底面积为s,圆柱底面积也是s,圆锥的高是h,圆柱的高也是h
圆锥的体积是:sh
圆柱的体积是:sh
圆锥的体积∶圆柱的体积=sh∶sh
=
=1∶3
底面积与高一样的圆锥和圆柱体积比为1∶3;
原题干底面积与高一样的圆锥和圆柱体积比为1∶2,说法错误。
故答案为:×
【点睛】
本题考查等底等高圆锥与圆柱体积的关系,根据圆锥、圆柱的体积公式进行解答。
14.√
【解析】
【分析】
圆锥纵切面是一个三角形,三角形的底是圆锥底面直径,三角形高是圆锥的高,如果圆锥的底面半径和高相等,纵切面如图,切面是一个等腰直角三角形。
【详解】
根据分析,一个圆锥的底面半径和高相等,过顶点和直径把这个圆锥切开,切面一定是等腰直角三角形,说法正确。
故答案为:√
【点睛】
关键是熟悉圆锥特征,想清楚纵切面和圆锥之间的关系。
15.×
【解析】
【分析】
圆柱的体积=底面积×高,圆锥的体积=圆锥的体积=×底面积×高,据此解答。
【详解】
根据分析可知,圆锥圆柱的体积都等于它们的底面积乘以高,说法错误。
故答案为:×
【点睛】
考查了圆柱和圆锥的体积,学生应熟练掌握。
16.×
【解析】
【分析】
因为等底等高的圆锥的体积是圆柱体积的,可以通过举例证明。
【详解】
假设一个圆柱的底面积是12.56平方厘米,高是9厘米,体积是12.56×9=113.04(立方厘米),
如果圆锥的体积是113.04立方厘米,底面积是12.56平方厘米,
那么圆锥的高是:113.04÷÷12.56
=113.04×3÷12.56
=339.12÷12.56
=27(厘米);
因此,圆柱和圆锥的体积相等,它们的高不一定相等。
故答案为:×
【点睛】
理解掌握等底等高的圆锥的体积是圆柱体积的是解答关键。
17.25厘米
【解析】
【分析】
由题意可知:圆锥体铁块的体积就等于上升3厘米的水的体积,将数据带入圆柱的体积公式:V=sh=πr2h,求出高3厘米的水的体积(圆锥的体积),再根据圆锥的体积公式:V=sh=πr2h,求出圆锥的高即可。
【详解】
3.14×102×3÷÷(3.14×62)
=3.14×102×3×3÷3.14÷62
=900÷36
=25(厘米)
答:这个圆锥体铁块的高是25厘米。
【点睛】
本题主要考查体积的等积变形,灵活运用圆柱、圆锥的体积公式是解题的关键。
18.197.82立方分米
【解析】
【分析】
将下图沿着虚线旋转一周,得到的立体图形是一个圆锥和一个圆柱组合而成,根据根据圆柱的体积公式:V=Sh(圆柱的高);圆锥的体积公式:V=Sh(圆锥的高),把数代入即可求解。
【详解】
圆锥的体积:3.14×3×3×3×
=9.42×3×3×
=28.26(立方分米)
圆柱的体积:3.14×3×3×6
=28.26×6
=169.56(立方分米)
169.56+28.26=197.82(立方分米)
答:旋转后的立体图形的体积是197.82立方分米。
【点睛】
本题主要考查圆柱和圆锥的体积公式,熟练掌握它们的体积公式并灵活运用。
19.0.28厘米
【解析】
【分析】
根据圆锥的体积公式:V=πr2h,求出圆锥体铅锤的体积,用圆锥体铅锤的体积除以圆柱形玻璃杯的底面积即可。
【详解】
3.14×(8÷2)2×12×÷[3.14×(30÷2)2]
=3.14×16×12×÷[3.14×225]
=50.24×12×÷706.5
=602.88×÷706.5
=200.96÷706.5
≈0.28(厘米)
答:杯里的水下降0.28厘米。
【点睛】
此题主要考查圆锥体积公式和圆柱体的体积公式的灵活运用,关键是熟记公式。
答案第1页,共2页
答案第1页,共2页
