北师大版六年级下册3.2图形的旋转(二)同步练习(含答案)
文档属性
| 名称 | 北师大版六年级下册3.2图形的旋转(二)同步练习(含答案) | 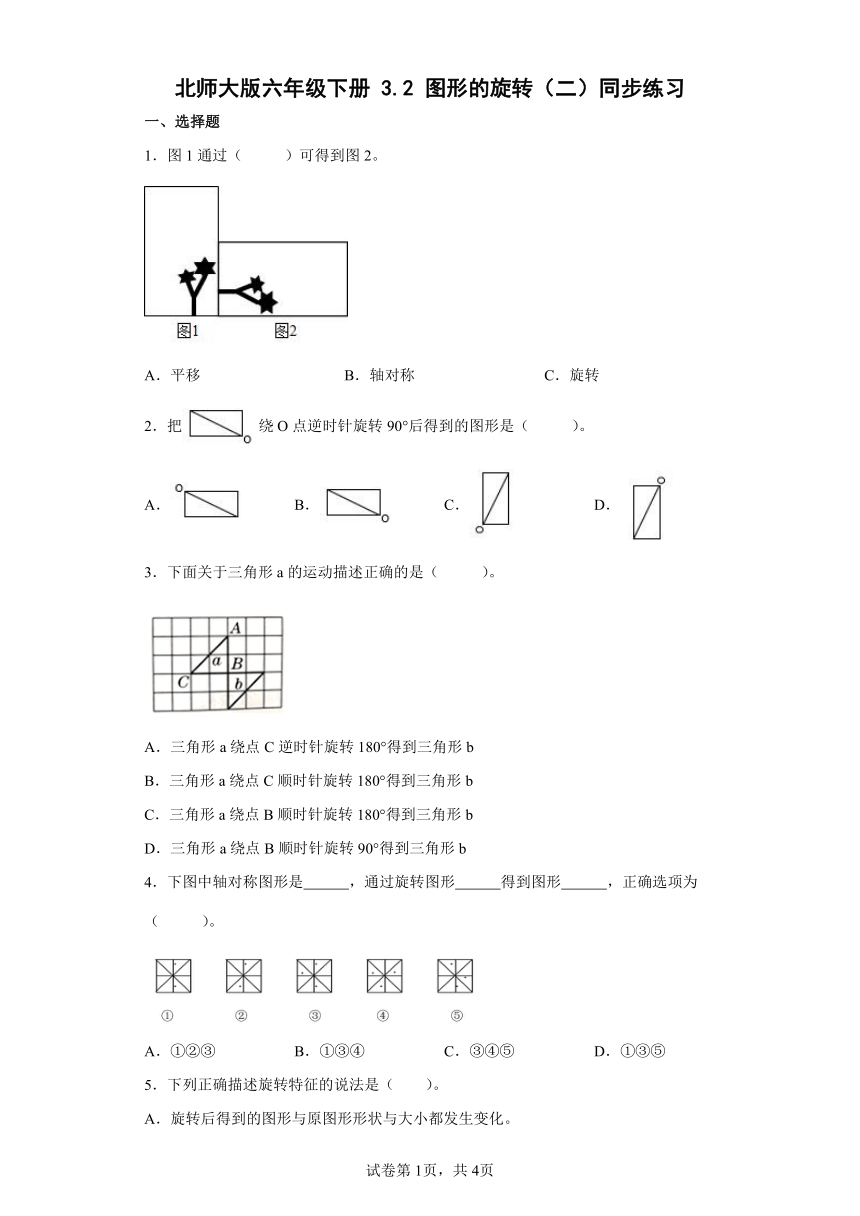 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 12:05:40 | ||
图片预览




文档简介
北师大版六年级下册 3.2 图形的旋转(二)同步练习
一、选择题
1.图1通过( )可得到图2。
A.平移 B.轴对称 C.旋转
2.把绕O点逆时针旋转90°后得到的图形是( )。
A. B. C. D.
3.下面关于三角形a的运动描述正确的是( )。
A.三角形a绕点C逆时针旋转180°得到三角形b
B.三角形a绕点C顺时针旋转180°得到三角形b
C.三角形a绕点B顺时针旋转180°得到三角形b
D.三角形a绕点B顺时针旋转90°得到三角形b
4.下图中轴对称图形是 ,通过旋转图形 得到图形 ,正确选项为( )。
A.①②③ B.①③④ C.③④⑤ D.①③⑤
5.下列正确描述旋转特征的说法是( )。
A.旋转后得到的图形与原图形形状与大小都发生变化。
B.旋转后得到的图形与原图形形状不变,大小发生变化。
C.旋转后得到的图形与原图形形状发生变化,大小不变。
D.旋转后得到的图形与原图形形状与大小都没有变化。
二、填空题
6.图中,图形①绕点逆时针旋转,到图形( )所在的位置。
图中,图形②绕点逆时针旋转( ),到图形③所在的位置。
7.
(1)图形A绕点O顺时针旋转( )°得到图形B。
(2)图形B绕点O( )时针旋转( )°得到图形C。
(3)图形C绕点O顺时针旋转90°得到图形( )。
(4)图形A绕点O( )时针旋转( )°得到图形D。
8.钟表的时针从“1”到“3”,是按( )方向旋转了( )度。
9.如图所示,原图旋转________次才会第一次出现。
10.如下图所示,图①沿逆时针方向旋转90°可得到图( );图①按顺时针方向至少旋转( )可得图⑤。
三、判断题
11.把一个图形绕某点顺时针旋转90°后,得到的图形与原来的图形相比,大小不变。( )
12.如图,图形A绕O点逆时针旋转90°后,到达图形B的位置。( )
13.只能通过轴对称得到。( )
14.所有的图形以任意一点为中心旋转360°都能与原来的图形完全重合. ( )
15.通过平移、轴对称和旋转可以改变图形的位置,但不能改变图形的大小、形状.( )
四、解答题
16.图中每个小方格表示1平方厘米。
(1)算出梯形的面积是( )平方厘米。
(2)画出梯形绕点顺时针旋转后的图形。
(3)画出梯形按的比放大后的图形。
17.在五年级数学直播课上,刘老师让同学们按要求进行画图。
(1)把图1绕点O顺时针旋转90°,得到图2。
(2)把图1绕点O逆时针旋转90°,得到图3。
(3)把图2绕点O顺时针旋转90°,得到图4。
(4)把图1,图2,图3,图4都涂上红色。看到这个图形你想到了什么?
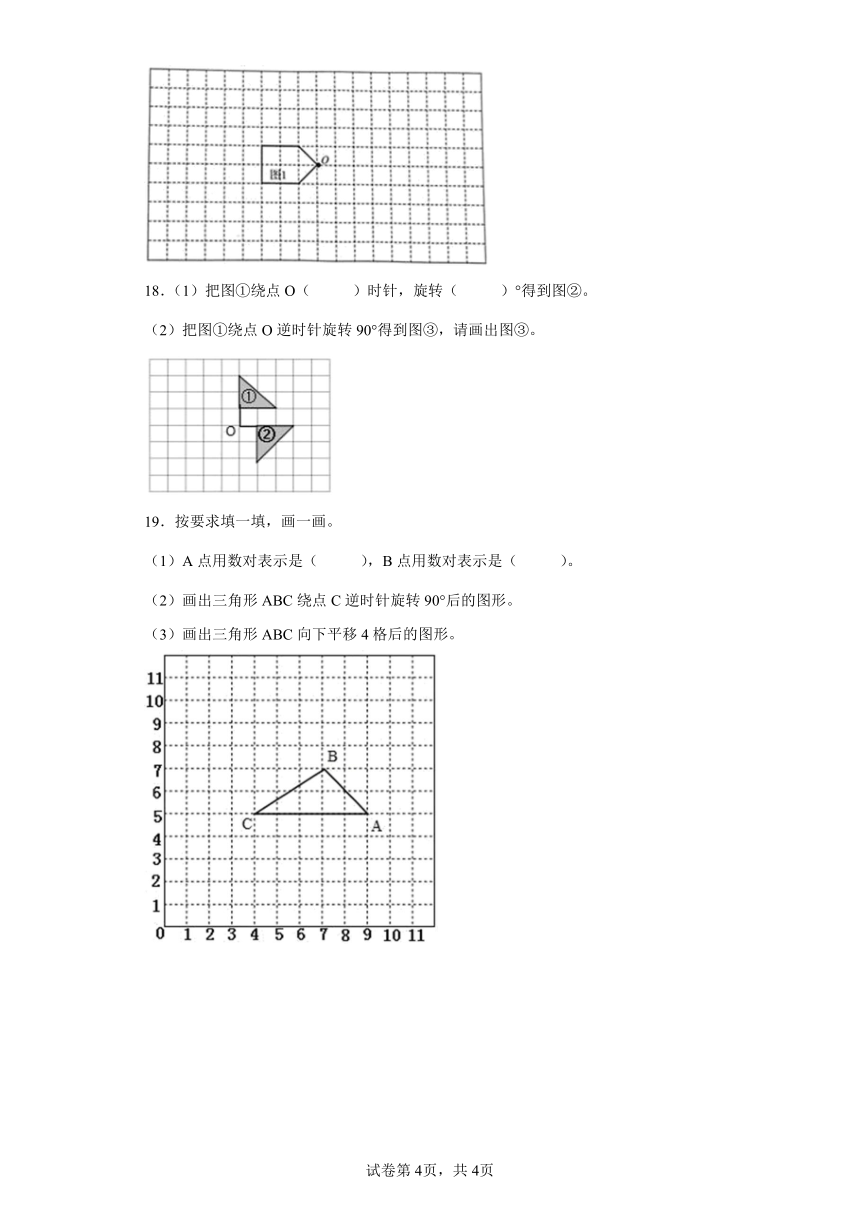
18.(1)把图①绕点O( )时针,旋转( )°得到图②。
(2)把图①绕点O逆时针旋转90°得到图③,请画出图③。
19.按要求填一填,画一画。
(1)A点用数对表示是( ),B点用数对表示是( )。
(2)画出三角形ABC绕点C逆时针旋转90°后的图形。
(3)画出三角形ABC向下平移4格后的图形。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
观察图1和图2可发现:图1绕右下角顶点顺时针旋转90°后,和图2完全重合,即图1通过旋转可得到图2,据此作答。
【详解】
A.根据平移的特点,图1中每一个点都要平移,和图1中右下角顶点不动相矛盾,所以本选项错误
B.图1和图2不是轴对称图形,图2不是图1通过轴对称得到的,所以本选项错误
C.图1绕右下角顶点顺时针旋转90°后得到图2
故答案为:C
【点睛】
本题考查图形的旋转,主要把握旋转的三要素。
2.D
【解析】
【分析】
旋转:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫作图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变,据此解答即可。
【详解】
把绕O点逆时针旋转90°后得到的图形是。
故答案选:D
【点评】
此题考查了旋转的意义及在实际当中的运用。
3.C
【解析】
【分析】
观察图可知:三角形a和三角形b有一个公共点B,所以三角形a是围绕点B旋转的。再对照旋转前后图形的特点即可得出正确的结论。
【详解】
A、B均是围绕点C旋转的,与题意分析不符,所以错误
D.观察三角形a和三角形b,可知三角形b是由三角形a旋转180°得到的,不是90°,所以错误
故答案为:C
【点睛】
本题考察图形的旋转,注意把握旋转三要素:方向、角度和旋转中心。
4.B
【解析】
观察各个图形中点的个数和位置,根据轴对称和旋转变换的定义进行解答。
【详解】
只有图①可以沿着米字格中间的横线折叠后完全重合,所以只有①是轴对称图形;
图①、②都有两个点,但两个点的位置分别分布在田字格中间竖线的同侧和异侧,所以它们不能通过旋转得到,图③、④、⑤均有3个点,观察点的位置可知图③、④中点的位置分布相同,并且图③逆时针旋转90°可以得到图④。
故答案为:B
【点睛】
本题考查轴对称和旋转变换,注意观察图形中点的位置分布是解题关键。
5.D
【解析】
【详解】
略
6. ④ 270°
【解析】
【分析】
根据旋转的特征,一个图形绕某点按一定的方向旋转一定的度数后,某点的位置不动,其余各部分均绕此点按相同的方向旋转相同的度数,图形①绕点O逆时针旋转90°到图形④所在位置;图形②绕点O逆时针旋转270°,到图形③所在位置。
【详解】
根据分析可知,图中,图形①绕点O逆时针旋转90°,到图形④所在位置;
图中,图形②绕点O逆时针旋转270°,到图形③所在位置。
【点睛】
此题主要是考查旋转的意义及特征。
7. 90 顺 90 D 逆 90
【解析】
【分析】
根据旋转的特征,一个图形绕某点按一定的方向旋转一定的度数后,某点的位置不动,其余各部分均绕此点按相同方向旋转相同的度数;据此解答。
【详解】
由图可知:
(1)图形A绕点O顺时针旋转90°得到图形B。
(2)图形B绕点O顺时针旋转90°得到图形C。
(3)图形C绕点O顺时针旋转90°得到图形D。
(4)图形A绕点O逆时针旋转90°得到图形D。
【点睛】
本题主要考查图形的旋转,注意旋转方向与旋转角度。
8. 顺时针 60
【解析】
【分析】
钟面上12个数字,以表芯为旋转点,表针转一圈是360°,被12个数字平均分成12份,每一份也就是两数之间夹角是30°;钟表的时针从“1”到“3”,是按顺时针方向旋转了30×2=60度。
【详解】
钟表的时针从“1”到“3”,是按顺时针方向旋转了60度。
【点睛】
此题考查了旋转的意义及在实际当中的运用。
9.5
【解析】
【分析】
观察图形知:每次都是顺时针旋转45度,第一次凸起指向右,第二次凸起指向右下、第三次凸起指向下,第四次凸起指向左下,第五次凸起指向左。据此解答。
【详解】
由分析知:原图旋转5次才会第一次出现。
【点睛】
主要考查了学生通过特例分析从而归纳总结出一般性结论的能力。对于找规律的题目应先找出哪些部分发生了变化,是按什么规律变化的,通过分析找到各部分的变化规律后直接用规律求解。
10. ⑤ 270°
【解析】
略
11.√
【解析】
【分析】
根据图形旋转的特征可知:图形旋转后,形状、大小都没有发生改变,只是位置发生的变化;据此解答。
【详解】
把一个图形绕某点顺时针旋转90°后,得到的图形与原来的图形相比,大小不变。原题干说法正确。
故答案为:√
【点睛】
本题考查旋转,明确旋转前后图形不变是解题的关键。
12.×
【解析】
【分析】
从图示可知:图形A要经过3次90度顺时针旋转,才能到过图形B的位置。据此解答。
【详解】
由分析的图示知:图形A要经过3次90度顺时针旋转,才能到过图形B的位置。故原题说法错误。
【点睛】
掌握图形的旋转方法是解答本题的关键。
13.×
【解析】
【分析】
根据旋转和轴对称的定义作答。
【详解】
可以通过旋转和轴对称得到。
故答案为:×
【点睛】
轴对称的特点是一个图形绕着一条直线对折,直线两旁的图形能够完全重合;旋转是指将一个图形绕着一点转动一个角度的变换。
14.√
【解析】
【详解】
略
15.√
【解析】
【详解】
略
16.(1)6平方厘米;
(2)(3)见详解
【解析】
【分析】
(1)每个小方格表示1平方厘米,则每格的长度是1厘米,根据梯形的面积=(上底+下底)×高÷2,计算即可;
(2)点O不动,其余各部分均绕点O顺时针旋转即可。
(3)把梯形的每条边都扩大到原来的2倍,画图即可。
【详解】
(1)
(平方厘米)
答:梯形的面积是6平方厘米;
(2)(3)如图所示:
【点睛】
此题考查了梯形的面积,旋转和图形的放缩,注意作放大后的图形是对应的每条边都扩大相同的倍数。
17.(1)(2)(3)图见详解
(4)想到了医院的红“十”字
【解析】
【分析】
(1)根据旋转的特征,图1绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图2。
(2)同理,图1绕点O逆时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图3。
(3)同理,即可画出图2绕点O顺时针旋转90°后的图4;
(4)图1,图2,图3,图4都涂上红色。
【详解】
(1)把图1绕点O顺时针旋转90°,得到图2(下图)。
(2)把图1绕点O逆时针旋转90°,得到图3(下图)。
(3)把图2绕点O顺时针旋转90°,得到图4(下图)。
(4)把图1,图2,图3,图4都涂上红色(下图)。看到这个图形“我”想到了医院的红“十”字。
【点睛】
旋转作图要注意:①旋转方向;②旋转角度。整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动。
18.(1)顺;90
(2)图见详解
【解析】
【分析】
(1)根据旋转的特征,图①绕点O顺时旋转90°即可得到图②。
(2)同理,图①绕点O逆时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【详解】
(1)把图①绕点O顺时针,旋转90°得到图②。
(2)把图①绕点O逆时针旋转90°得到图③,请画出图③(下图红色部分)。
【点睛】
旋转作图要注意:①旋转方向;②旋转角度。整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动。
19.(1)(9,5);(7,7)
(2)(3)见详解
【解析】
【分析】
(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可用数对分别表示出A、B的位置。
(2)根据旋转的特征,三角形ABC绕点C逆时针旋转90°,点C的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据平移的特征,把三角形ABC的各顶点分别向下平移4格,依次连结即可得到平移后的图形。
【详解】
(1)A点用数对表示是(9,5),B点用数对表示是(7,7)。
(2)画出三角形ABC绕点C逆时针旋转90°后的图形(图中红色部分)。
(3)画出三角形ABC向下平移4格后的图形(图中绿色部分)。
【点睛】
数对中每个数字所代表的意义,在不同的题目中会有所不同,但在无特殊说明的情况下,数对中第一个数字表示列,第二个数字表示行。图形平移注意三要素:即原位置、平移方向、平移距离。图形旋转注意四要素:即原位置、旋转中心、旋转方向、旋转角。
答案第1页,共2页
答案第1页,共2页
一、选择题
1.图1通过( )可得到图2。
A.平移 B.轴对称 C.旋转
2.把绕O点逆时针旋转90°后得到的图形是( )。
A. B. C. D.
3.下面关于三角形a的运动描述正确的是( )。
A.三角形a绕点C逆时针旋转180°得到三角形b
B.三角形a绕点C顺时针旋转180°得到三角形b
C.三角形a绕点B顺时针旋转180°得到三角形b
D.三角形a绕点B顺时针旋转90°得到三角形b
4.下图中轴对称图形是 ,通过旋转图形 得到图形 ,正确选项为( )。
A.①②③ B.①③④ C.③④⑤ D.①③⑤
5.下列正确描述旋转特征的说法是( )。
A.旋转后得到的图形与原图形形状与大小都发生变化。
B.旋转后得到的图形与原图形形状不变,大小发生变化。
C.旋转后得到的图形与原图形形状发生变化,大小不变。
D.旋转后得到的图形与原图形形状与大小都没有变化。
二、填空题
6.图中,图形①绕点逆时针旋转,到图形( )所在的位置。
图中,图形②绕点逆时针旋转( ),到图形③所在的位置。
7.
(1)图形A绕点O顺时针旋转( )°得到图形B。
(2)图形B绕点O( )时针旋转( )°得到图形C。
(3)图形C绕点O顺时针旋转90°得到图形( )。
(4)图形A绕点O( )时针旋转( )°得到图形D。
8.钟表的时针从“1”到“3”,是按( )方向旋转了( )度。
9.如图所示,原图旋转________次才会第一次出现。
10.如下图所示,图①沿逆时针方向旋转90°可得到图( );图①按顺时针方向至少旋转( )可得图⑤。
三、判断题
11.把一个图形绕某点顺时针旋转90°后,得到的图形与原来的图形相比,大小不变。( )
12.如图,图形A绕O点逆时针旋转90°后,到达图形B的位置。( )
13.只能通过轴对称得到。( )
14.所有的图形以任意一点为中心旋转360°都能与原来的图形完全重合. ( )
15.通过平移、轴对称和旋转可以改变图形的位置,但不能改变图形的大小、形状.( )
四、解答题
16.图中每个小方格表示1平方厘米。
(1)算出梯形的面积是( )平方厘米。
(2)画出梯形绕点顺时针旋转后的图形。
(3)画出梯形按的比放大后的图形。
17.在五年级数学直播课上,刘老师让同学们按要求进行画图。
(1)把图1绕点O顺时针旋转90°,得到图2。
(2)把图1绕点O逆时针旋转90°,得到图3。
(3)把图2绕点O顺时针旋转90°,得到图4。
(4)把图1,图2,图3,图4都涂上红色。看到这个图形你想到了什么?
18.(1)把图①绕点O( )时针,旋转( )°得到图②。
(2)把图①绕点O逆时针旋转90°得到图③,请画出图③。
19.按要求填一填,画一画。
(1)A点用数对表示是( ),B点用数对表示是( )。
(2)画出三角形ABC绕点C逆时针旋转90°后的图形。
(3)画出三角形ABC向下平移4格后的图形。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
【分析】
观察图1和图2可发现:图1绕右下角顶点顺时针旋转90°后,和图2完全重合,即图1通过旋转可得到图2,据此作答。
【详解】
A.根据平移的特点,图1中每一个点都要平移,和图1中右下角顶点不动相矛盾,所以本选项错误
B.图1和图2不是轴对称图形,图2不是图1通过轴对称得到的,所以本选项错误
C.图1绕右下角顶点顺时针旋转90°后得到图2
故答案为:C
【点睛】
本题考查图形的旋转,主要把握旋转的三要素。
2.D
【解析】
【分析】
旋转:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫作图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。旋转前后图形的位置和方向改变,形状、大小不变,据此解答即可。
【详解】
把绕O点逆时针旋转90°后得到的图形是。
故答案选:D
【点评】
此题考查了旋转的意义及在实际当中的运用。
3.C
【解析】
【分析】
观察图可知:三角形a和三角形b有一个公共点B,所以三角形a是围绕点B旋转的。再对照旋转前后图形的特点即可得出正确的结论。
【详解】
A、B均是围绕点C旋转的,与题意分析不符,所以错误
D.观察三角形a和三角形b,可知三角形b是由三角形a旋转180°得到的,不是90°,所以错误
故答案为:C
【点睛】
本题考察图形的旋转,注意把握旋转三要素:方向、角度和旋转中心。
4.B
【解析】
观察各个图形中点的个数和位置,根据轴对称和旋转变换的定义进行解答。
【详解】
只有图①可以沿着米字格中间的横线折叠后完全重合,所以只有①是轴对称图形;
图①、②都有两个点,但两个点的位置分别分布在田字格中间竖线的同侧和异侧,所以它们不能通过旋转得到,图③、④、⑤均有3个点,观察点的位置可知图③、④中点的位置分布相同,并且图③逆时针旋转90°可以得到图④。
故答案为:B
【点睛】
本题考查轴对称和旋转变换,注意观察图形中点的位置分布是解题关键。
5.D
【解析】
【详解】
略
6. ④ 270°
【解析】
【分析】
根据旋转的特征,一个图形绕某点按一定的方向旋转一定的度数后,某点的位置不动,其余各部分均绕此点按相同的方向旋转相同的度数,图形①绕点O逆时针旋转90°到图形④所在位置;图形②绕点O逆时针旋转270°,到图形③所在位置。
【详解】
根据分析可知,图中,图形①绕点O逆时针旋转90°,到图形④所在位置;
图中,图形②绕点O逆时针旋转270°,到图形③所在位置。
【点睛】
此题主要是考查旋转的意义及特征。
7. 90 顺 90 D 逆 90
【解析】
【分析】
根据旋转的特征,一个图形绕某点按一定的方向旋转一定的度数后,某点的位置不动,其余各部分均绕此点按相同方向旋转相同的度数;据此解答。
【详解】
由图可知:
(1)图形A绕点O顺时针旋转90°得到图形B。
(2)图形B绕点O顺时针旋转90°得到图形C。
(3)图形C绕点O顺时针旋转90°得到图形D。
(4)图形A绕点O逆时针旋转90°得到图形D。
【点睛】
本题主要考查图形的旋转,注意旋转方向与旋转角度。
8. 顺时针 60
【解析】
【分析】
钟面上12个数字,以表芯为旋转点,表针转一圈是360°,被12个数字平均分成12份,每一份也就是两数之间夹角是30°;钟表的时针从“1”到“3”,是按顺时针方向旋转了30×2=60度。
【详解】
钟表的时针从“1”到“3”,是按顺时针方向旋转了60度。
【点睛】
此题考查了旋转的意义及在实际当中的运用。
9.5
【解析】
【分析】
观察图形知:每次都是顺时针旋转45度,第一次凸起指向右,第二次凸起指向右下、第三次凸起指向下,第四次凸起指向左下,第五次凸起指向左。据此解答。
【详解】
由分析知:原图旋转5次才会第一次出现。
【点睛】
主要考查了学生通过特例分析从而归纳总结出一般性结论的能力。对于找规律的题目应先找出哪些部分发生了变化,是按什么规律变化的,通过分析找到各部分的变化规律后直接用规律求解。
10. ⑤ 270°
【解析】
略
11.√
【解析】
【分析】
根据图形旋转的特征可知:图形旋转后,形状、大小都没有发生改变,只是位置发生的变化;据此解答。
【详解】
把一个图形绕某点顺时针旋转90°后,得到的图形与原来的图形相比,大小不变。原题干说法正确。
故答案为:√
【点睛】
本题考查旋转,明确旋转前后图形不变是解题的关键。
12.×
【解析】
【分析】
从图示可知:图形A要经过3次90度顺时针旋转,才能到过图形B的位置。据此解答。
【详解】
由分析的图示知:图形A要经过3次90度顺时针旋转,才能到过图形B的位置。故原题说法错误。
【点睛】
掌握图形的旋转方法是解答本题的关键。
13.×
【解析】
【分析】
根据旋转和轴对称的定义作答。
【详解】
可以通过旋转和轴对称得到。
故答案为:×
【点睛】
轴对称的特点是一个图形绕着一条直线对折,直线两旁的图形能够完全重合;旋转是指将一个图形绕着一点转动一个角度的变换。
14.√
【解析】
【详解】
略
15.√
【解析】
【详解】
略
16.(1)6平方厘米;
(2)(3)见详解
【解析】
【分析】
(1)每个小方格表示1平方厘米,则每格的长度是1厘米,根据梯形的面积=(上底+下底)×高÷2,计算即可;
(2)点O不动,其余各部分均绕点O顺时针旋转即可。
(3)把梯形的每条边都扩大到原来的2倍,画图即可。
【详解】
(1)
(平方厘米)
答:梯形的面积是6平方厘米;
(2)(3)如图所示:
【点睛】
此题考查了梯形的面积,旋转和图形的放缩,注意作放大后的图形是对应的每条边都扩大相同的倍数。
17.(1)(2)(3)图见详解
(4)想到了医院的红“十”字
【解析】
【分析】
(1)根据旋转的特征,图1绕点O顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图2。
(2)同理,图1绕点O逆时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图3。
(3)同理,即可画出图2绕点O顺时针旋转90°后的图4;
(4)图1,图2,图3,图4都涂上红色。
【详解】
(1)把图1绕点O顺时针旋转90°,得到图2(下图)。
(2)把图1绕点O逆时针旋转90°,得到图3(下图)。
(3)把图2绕点O顺时针旋转90°,得到图4(下图)。
(4)把图1,图2,图3,图4都涂上红色(下图)。看到这个图形“我”想到了医院的红“十”字。
【点睛】
旋转作图要注意:①旋转方向;②旋转角度。整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动。
18.(1)顺;90
(2)图见详解
【解析】
【分析】
(1)根据旋转的特征,图①绕点O顺时旋转90°即可得到图②。
(2)同理,图①绕点O逆时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
【详解】
(1)把图①绕点O顺时针,旋转90°得到图②。
(2)把图①绕点O逆时针旋转90°得到图③,请画出图③(下图红色部分)。
【点睛】
旋转作图要注意:①旋转方向;②旋转角度。整个旋转作图,就是把整个图案的每一个特征点绕旋转中心按一定的旋转方向和一定的旋转角度旋转移动。
19.(1)(9,5);(7,7)
(2)(3)见详解
【解析】
【分析】
(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可用数对分别表示出A、B的位置。
(2)根据旋转的特征,三角形ABC绕点C逆时针旋转90°,点C的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)根据平移的特征,把三角形ABC的各顶点分别向下平移4格,依次连结即可得到平移后的图形。
【详解】
(1)A点用数对表示是(9,5),B点用数对表示是(7,7)。
(2)画出三角形ABC绕点C逆时针旋转90°后的图形(图中红色部分)。
(3)画出三角形ABC向下平移4格后的图形(图中绿色部分)。
【点睛】
数对中每个数字所代表的意义,在不同的题目中会有所不同,但在无特殊说明的情况下,数对中第一个数字表示列,第二个数字表示行。图形平移注意三要素:即原位置、平移方向、平移距离。图形旋转注意四要素:即原位置、旋转中心、旋转方向、旋转角。
答案第1页,共2页
答案第1页,共2页
