小学数学苏教版四年级上册 《商不变定律》表格式教案
文档属性
| 名称 | 小学数学苏教版四年级上册 《商不变定律》表格式教案 | 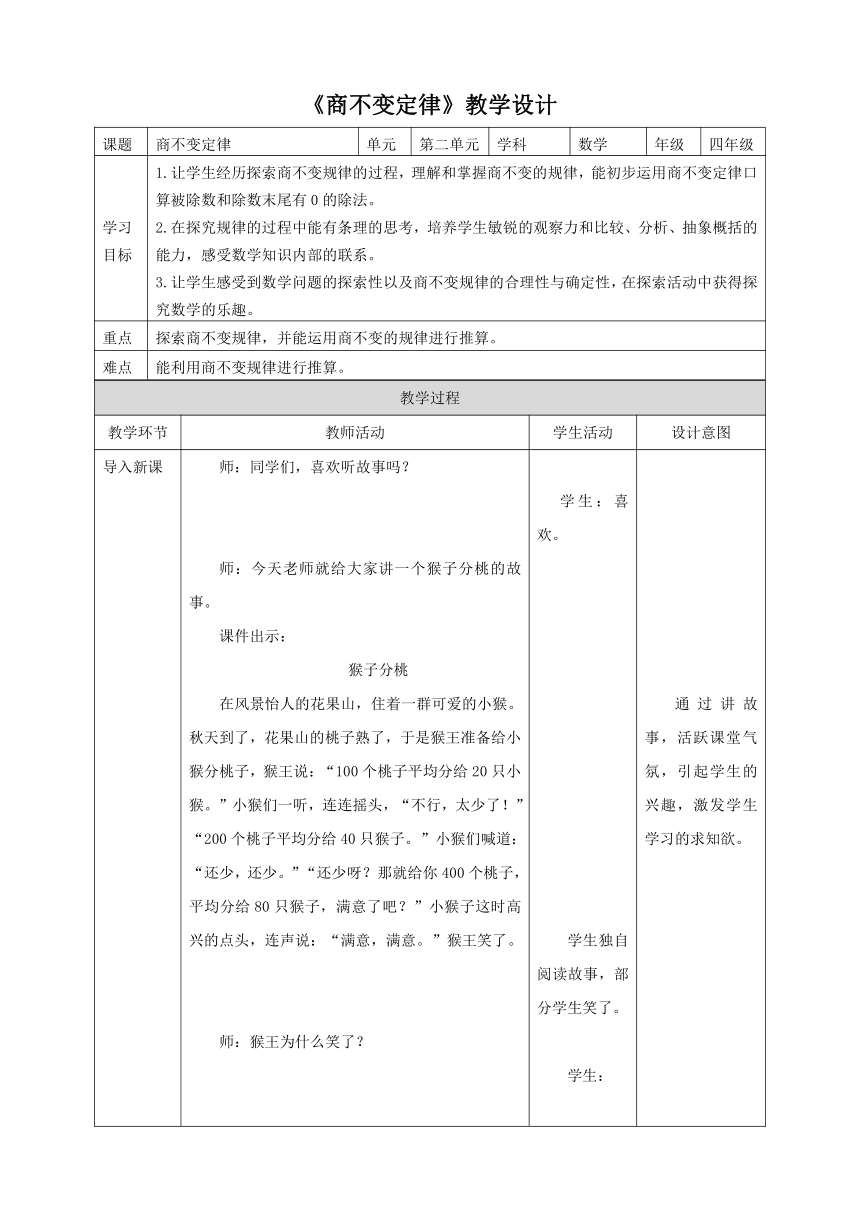 | |
| 格式 | docx | ||
| 文件大小 | 162.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 06:40:27 | ||
图片预览



文档简介
《商不变定律》教学设计
课题 商不变定律 单元 第二单元 学科 数学 年级 四年级
学习 目标 1.让学生经历探索商不变规律的过程,理解和掌握商不变的规律,能初步运用商不变定律口算被除数和除数末尾有0的除法。 2.在探究规律的过程中能有条理的思考,培养学生敏锐的观察力和比较、分析、抽象概括的能力,感受数学知识内部的联系。 3.让学生感受到数学问题的探索性以及商不变规律的合理性与确定性,在探索活动中获得探究数学的乐趣。
重点 探索商不变规律,并能运用商不变的规律进行推算。
难点 能利用商不变规律进行推算。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 师:同学们,喜欢听故事吗? 师:今天老师就给大家讲一个猴子分桃的故事。 课件出示: 猴子分桃 在风景怡人的花果山,住着一群可爱的小猴。秋天到了,花果山的桃子熟了,于是猴王准备给小猴分桃子,猴王说:“100个桃子平均分给20只小猴。”小猴们一听,连连摇头,“不行,太少了!”“200个桃子平均分给40只猴子。”小猴们喊道:“还少,还少。”“还少呀?那就给你400个桃子,平均分给80只猴子,满意了吧?”小猴子这时高兴的点头,连声说:“满意,满意。”猴王笑了。 师:猴王为什么笑了? 学生:喜欢。 学生独自阅读故事,部分学生笑了。 学生: 通过讲故事,活跃课堂气氛,引起学生的兴趣,激发学生学习的求知欲。
师:是这样吗?我们一起来看看好吗? 因为无论怎样分,每个猴子吃到的个数都一样,都是5个。
讲授新课 探究商不变的规律 师:我把刚才的信息全部放进了表格,先按要求算一算,填一填,再比较算出的结果。 课件出示: 师:还真是每个猴子吃到的个数都是5个呀!真聪明。看到这个表,大家还有什么想知道的吗? 师:这个问题问的真好!我们一起来算算看。 课件出示: 师:被除数和除数怎样变化的?商呢?你有什么发现? 学生按要求独自计算,然后集体反馈。 学生:如果被除数和除数变小,商会有变化吗? 学生按要求独自计算,然后集体反馈。 学生自由说说。 通过算一算,填一填,比一比,初步感受被除数和除数、商的变化,培养学生观察、分析、比较、总结、归纳等思维能力。
反馈: 被除数和除数同时乘2或乘4,商不变。 被除数和除数同时除以2或除以4,商不变。 被除数和除数同时乘或除以同一个数,商不变。 师:自己再找一些例子,算一算,比一比,看商有没有变化,与同学交流。 师:老师也找了一个,你们看看对吗? 40÷5=8 (40÷0)÷(5÷0)=0 (40×0)÷(5×0)=0 反馈: 0不能做除数,这样不对,而且商也变了。 我知道了被除数和除数同时乘或除以一个相同的数(0除外),商不变。 师:同时乘或除以一个数,这个数为什么不包括0? 师:说得真好!我们发现的这个规律在数学中称之为商不变定律,用字母表示为:a÷b=(a×c)÷(b×c)=(a÷c)÷(b÷c)(c≠0)。 学生举例子,然后展示交流。 学生独自观察,然后自由说说。 学生:这个数为0,除数就变成0,没有意义了,而且商也变了。 通过举例,深化学生对商不变规律的认识与理解,感受数学知识内部的联系。 通过老师举例引入,让学生充分感受同时乘或除以一个数,这个数不为0的理由,强化学生对商不变规律的进一步认识。
课堂练习
1.先说说被除数和除数分别是怎样变化的,再直接填出商。 2.填一填。 160÷80=(160÷10)÷(80÷10)=( ) 340÷170=(340÷10)÷(170÷___)=( ) 9600÷600=(9600÷___)÷(600÷100)=( ) 2400÷1200==(2400÷___)÷(1200÷100)=( ) 3.直接写出下面两题的商。 32÷4= 6÷3= 1400÷70= 320÷40= 60÷30= 140÷70= 3200÷40= 600÷300= 14÷7= 4.利用商不变的规律简算。 200÷25 =(200×4)÷(25×4) =800÷100 =8 算一算:6000÷125 学生独自完成,然后集体订正。 设计不同类型的练习,检查学生掌握知识的情况,同时提高学生运用知识解决问题的能力。
课堂小结 说说这节课你有什么收获? 学生自由说说。 通过说一说,帮助学生回忆已经学过的知识,形成完整的知识体系。
板书 商不变定律 100÷20=5 (100×2)÷(20×2)=5 (100×4)÷(20×4)=5 (100÷2)÷(20÷2)=5 (100÷4)÷(20÷4)=5 板书的设计凸显了本课学习的重点与难点,明确本节课学习的内容。
被除数和除数同时乘或除以一个相同的数(0除外),商不变,这叫做商不变定律。 a÷b =(a×c)÷(b×c) =(a÷c)÷(b÷c)(c≠0)
课题 商不变定律 单元 第二单元 学科 数学 年级 四年级
学习 目标 1.让学生经历探索商不变规律的过程,理解和掌握商不变的规律,能初步运用商不变定律口算被除数和除数末尾有0的除法。 2.在探究规律的过程中能有条理的思考,培养学生敏锐的观察力和比较、分析、抽象概括的能力,感受数学知识内部的联系。 3.让学生感受到数学问题的探索性以及商不变规律的合理性与确定性,在探索活动中获得探究数学的乐趣。
重点 探索商不变规律,并能运用商不变的规律进行推算。
难点 能利用商不变规律进行推算。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 师:同学们,喜欢听故事吗? 师:今天老师就给大家讲一个猴子分桃的故事。 课件出示: 猴子分桃 在风景怡人的花果山,住着一群可爱的小猴。秋天到了,花果山的桃子熟了,于是猴王准备给小猴分桃子,猴王说:“100个桃子平均分给20只小猴。”小猴们一听,连连摇头,“不行,太少了!”“200个桃子平均分给40只猴子。”小猴们喊道:“还少,还少。”“还少呀?那就给你400个桃子,平均分给80只猴子,满意了吧?”小猴子这时高兴的点头,连声说:“满意,满意。”猴王笑了。 师:猴王为什么笑了? 学生:喜欢。 学生独自阅读故事,部分学生笑了。 学生: 通过讲故事,活跃课堂气氛,引起学生的兴趣,激发学生学习的求知欲。
师:是这样吗?我们一起来看看好吗? 因为无论怎样分,每个猴子吃到的个数都一样,都是5个。
讲授新课 探究商不变的规律 师:我把刚才的信息全部放进了表格,先按要求算一算,填一填,再比较算出的结果。 课件出示: 师:还真是每个猴子吃到的个数都是5个呀!真聪明。看到这个表,大家还有什么想知道的吗? 师:这个问题问的真好!我们一起来算算看。 课件出示: 师:被除数和除数怎样变化的?商呢?你有什么发现? 学生按要求独自计算,然后集体反馈。 学生:如果被除数和除数变小,商会有变化吗? 学生按要求独自计算,然后集体反馈。 学生自由说说。 通过算一算,填一填,比一比,初步感受被除数和除数、商的变化,培养学生观察、分析、比较、总结、归纳等思维能力。
反馈: 被除数和除数同时乘2或乘4,商不变。 被除数和除数同时除以2或除以4,商不变。 被除数和除数同时乘或除以同一个数,商不变。 师:自己再找一些例子,算一算,比一比,看商有没有变化,与同学交流。 师:老师也找了一个,你们看看对吗? 40÷5=8 (40÷0)÷(5÷0)=0 (40×0)÷(5×0)=0 反馈: 0不能做除数,这样不对,而且商也变了。 我知道了被除数和除数同时乘或除以一个相同的数(0除外),商不变。 师:同时乘或除以一个数,这个数为什么不包括0? 师:说得真好!我们发现的这个规律在数学中称之为商不变定律,用字母表示为:a÷b=(a×c)÷(b×c)=(a÷c)÷(b÷c)(c≠0)。 学生举例子,然后展示交流。 学生独自观察,然后自由说说。 学生:这个数为0,除数就变成0,没有意义了,而且商也变了。 通过举例,深化学生对商不变规律的认识与理解,感受数学知识内部的联系。 通过老师举例引入,让学生充分感受同时乘或除以一个数,这个数不为0的理由,强化学生对商不变规律的进一步认识。
课堂练习
1.先说说被除数和除数分别是怎样变化的,再直接填出商。 2.填一填。 160÷80=(160÷10)÷(80÷10)=( ) 340÷170=(340÷10)÷(170÷___)=( ) 9600÷600=(9600÷___)÷(600÷100)=( ) 2400÷1200==(2400÷___)÷(1200÷100)=( ) 3.直接写出下面两题的商。 32÷4= 6÷3= 1400÷70= 320÷40= 60÷30= 140÷70= 3200÷40= 600÷300= 14÷7= 4.利用商不变的规律简算。 200÷25 =(200×4)÷(25×4) =800÷100 =8 算一算:6000÷125 学生独自完成,然后集体订正。 设计不同类型的练习,检查学生掌握知识的情况,同时提高学生运用知识解决问题的能力。
课堂小结 说说这节课你有什么收获? 学生自由说说。 通过说一说,帮助学生回忆已经学过的知识,形成完整的知识体系。
板书 商不变定律 100÷20=5 (100×2)÷(20×2)=5 (100×4)÷(20×4)=5 (100÷2)÷(20÷2)=5 (100÷4)÷(20÷4)=5 板书的设计凸显了本课学习的重点与难点,明确本节课学习的内容。
被除数和除数同时乘或除以一个相同的数(0除外),商不变,这叫做商不变定律。 a÷b =(a×c)÷(b×c) =(a÷c)÷(b÷c)(c≠0)
