2021—2022学年人教版九年级数学下册27.3位似课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版九年级数学下册27.3位似课后练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 441.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 08:36:13 | ||
图片预览



文档简介
2021——2022学年度人教版九年级数学下册 第二十七章 相似 27.3 位似课后练习
一、选择题
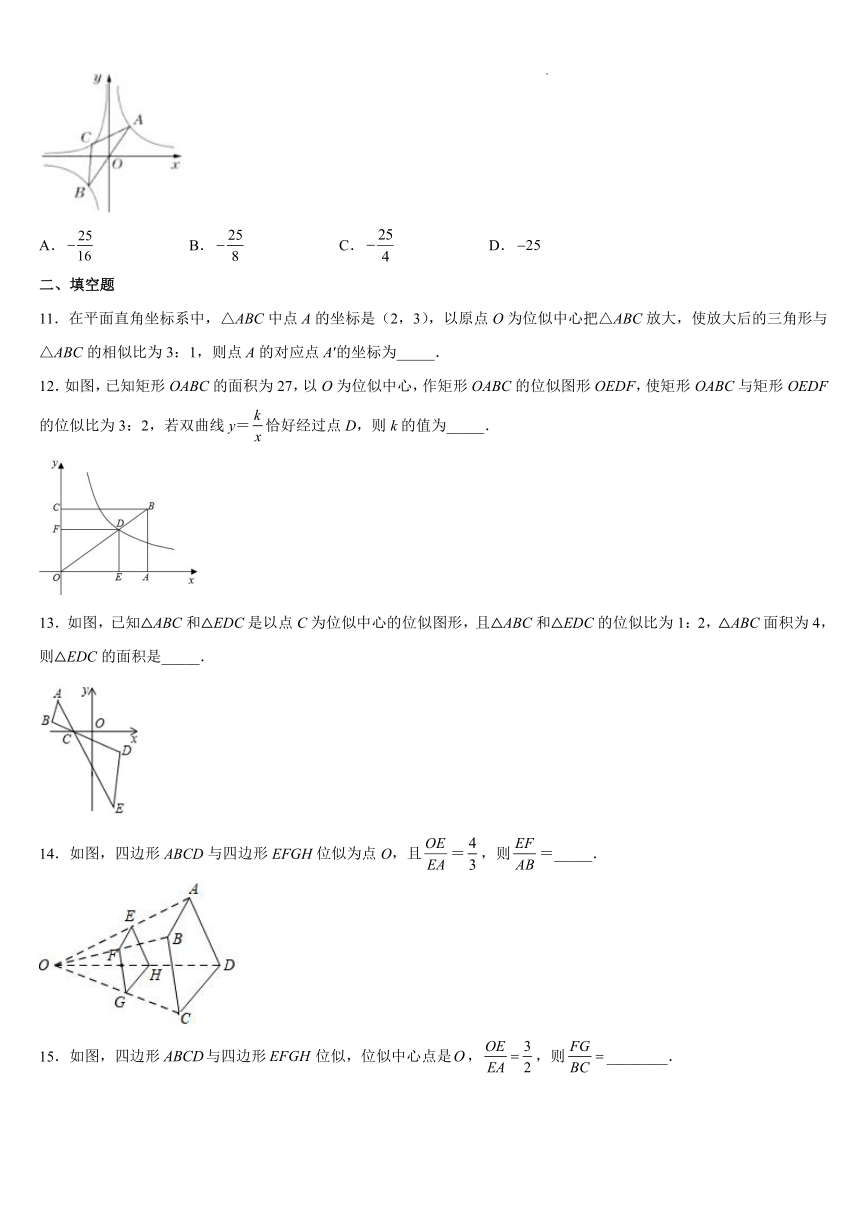
1.下列每组的两个图形中,不是位似图形的是( )
A. B. C. D.
2.如图,点是正三角形的中心,分别是的中点,则与是位似三角形,此时与的位似中心是( )
A.点O B.点P C.点 D.点Q
3.下列四边形和四边形是位似图形,它们的位似中心是( )
A.点E B.点F C.点G D.点D
4.如图,以点O为位似中心,把的各边长放大为原来的2倍得到,以下说法中错误的是( )
A. B.点在同一直线上
C. D.
5.如图,△ABC与△DEF是位似图形,点O为位似中心,已知BO:OE=2:1,则△ABC与△DEF的面积比是
( )
A.2:1 B.3:1 C.4:1 D.5:1
6.如图,已知△ABC与△DEF位似,位似中心为点O,OA:OD=1:3,且△ABC的周长为2,则△DEF的周长为( )
A.4 B.6 C.8 D.18
7.如图,在平面直角坐标系中,以点O为位似中心,将放大得到,点C、D的坐标分别为(2,1)、(2,0),且与的面积之比为1:4,则点A的坐标为( )
A.(8,4) B.(8,2) C.(4,2) D.(4,8)
8.如图,在平面直角坐标系中,与是以点为位似中心的位似图形,且相似比为1:2,点在轴上,若点的坐标是,点的坐标是,则点的坐标是( ).
A. B. C. D.
9.如图,在和是以点为位似中心的位似三角形,若为的中点,,则的长为( )
A. B. C. D.
10.如图,点,是双曲线图象上的两点,连接,线段经过点,点为双曲线在第二象限的分支上一点,当满足且时,的值为( ).
A. B. C. D.
二、填空题
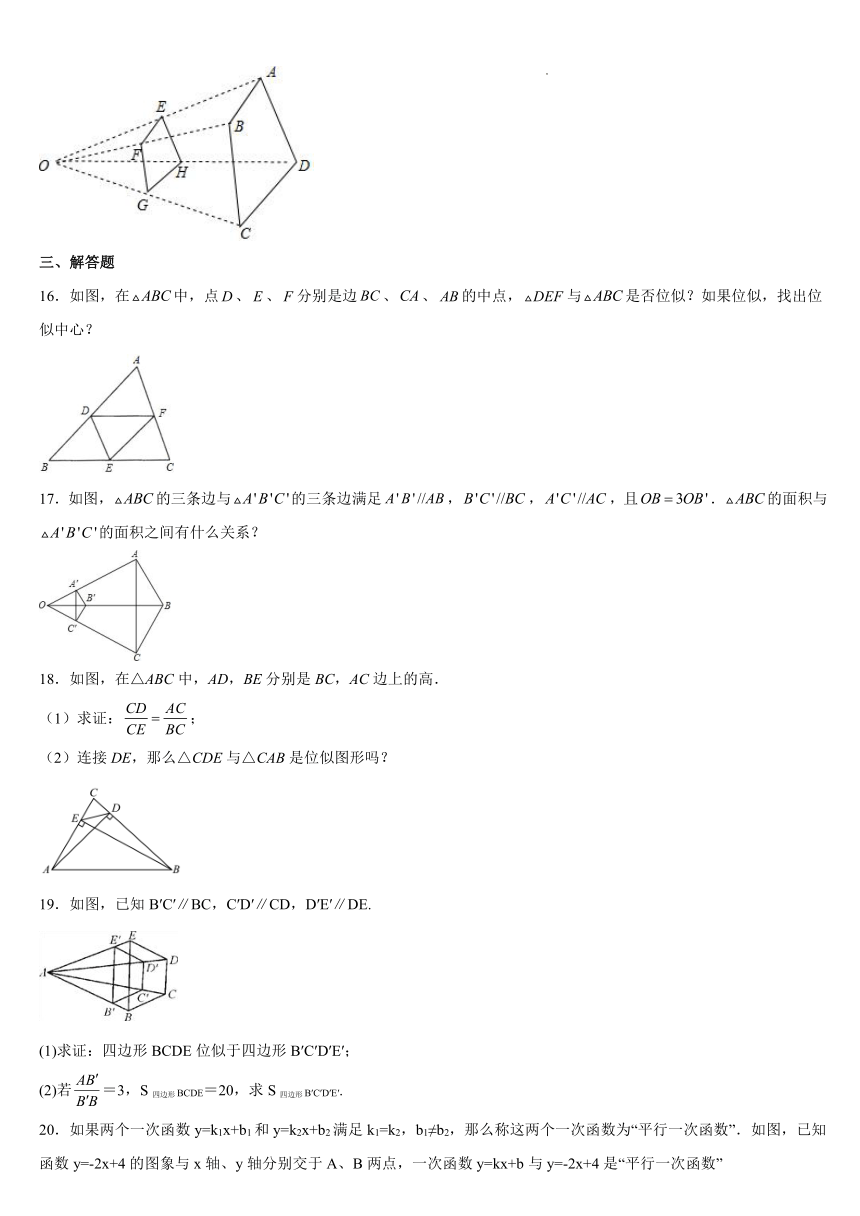
11.在平面直角坐标系中,△ABC中点A的坐标是(2,3),以原点O为位似中心把△ABC放大,使放大后的三角形与△ABC的相似比为3:1,则点A的对应点A′的坐标为_____.
12.如图,已知矩形OABC的面积为27,以O为位似中心,作矩形OABC的位似图形OEDF,使矩形OABC与矩形OEDF的位似比为3:2,若双曲线y=恰好经过点D,则k的值为_____.
13.如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为4,则△EDC的面积是_____.
14.如图,四边形ABCD与四边形EFGH位似为点O,且=,则=_____.
15.如图,四边形与四边形位似,位似中心点是,,则________.
三、解答题
16.如图,在中,点、、分别是边、、的中点,与是否位似?如果位似,找出位似中心?
17.如图,的三条边与的三条边满足,,,且.的面积与的面积之间有什么关系?
18.如图,在△ABC中,AD,BE分别是BC,AC边上的高.
(1)求证:;
(2)连接DE,那么△CDE与△CAB是位似图形吗?
19.如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
(1)求证:四边形BCDE位似于四边形B′C′D′E′;
(2)若=3,S四边形BCDE=20,求S四边形B′C′D′E′.
20.如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.如图,已知函数y=-2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=-2x+4是“平行一次函数”
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形,位似中心为原点,位似比为1:2,求函数y=kx+b的表达式.
21.如图,在带有网格的平面直角坐标系中,网格边长为一个单位长度,给出了三角形ABC.
(1)作出关于x轴对称的;
(2)以坐标原点为位似中心在图中的网格中作出的位似图形,使与的位似比为1:2;
(3)若的面积为3.5平方单位,求出的面积.
22.在平面直角坐标系中,△ABC的位置如图所示,每个小正方形的边长为1,以原点O为位似中心,在第一象限内,对△ABC进行位似变换,得到△DEF(点A,B,C分别对应点D,E,F),且△ABC与△DEF的相似比为2:1
(1)画出△DEF;
(2)线段AC上一点(x,y)经过变换后对应的点的坐标为________;
(3)求△DEF的周长.
23.如图,已知O是坐标原点,A,B两点的坐标分别为(2,1),(3,﹣1),
(1)以点O为位似中心,将△OAB放大为原来的两倍,画出图形;
(2)A点的对应点A'的坐标是 ;B点的对应点B′的坐标是 ;
(3)在AB上有一点P(x,y),按(1)的方式得到的对应点P′的坐标是 .
【参考答案】
1.B 2.A 3.D 4.A 5.C 6.B 7.C 8.C 9.B 10.B
11.或
12.12
13.16
14.
15..
16.与是位似图形,位似中心是点,
理由:∵点、、分别是边、、的中点,
∴,
∴,
∵连接、、交于一点,
故与是位似图形.
17.解:的面积为的面积的9倍.
证明:∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴
∴,
∴,
∴,且相似比为3,
∴与的面积比为9.
18.解:(1)证明:、是高,
,
,
,
;
(2)解:如图,
∵△CDE与△CAB不一定是相似三有形,
∴与不是位似图形.
19.(1)∵B′C′∥BC,C′D′∥CD,D′E′∥DE,
∴,
又∵四边形B′C′D′E′和BCDE中对应顶点的连线相交于点A,
∴四边形B′C′D′E′和BCDE是位似图形;
(2)∵,
∴,
又∵四边形B′C′D′E′和BCDE是位似图形,
∴四边形B′C′D′E′和BCDE的相似比为,
∴S四边形B′C′D′E′:S四边形BCDE=9:16,
又∵S四边形BCDE=20,
∴S四边形B′C′D′E′=.
20.(1)由已知得:k=﹣2,把点(3,1)和k=﹣2代入y=kx+b中得:1=﹣2×3+b,∴b=7;
(2)根据位似比为1:2得:函数y=kx+b的图象有两种情况:
①不经过第三象限时,过(1,0)和(0,2),这时表达示为:y=﹣2x+2;
②不经过第一象限时,过(﹣1,0)和(0,﹣2),这时表达示为:y=﹣2x﹣2;
21.解:(1)如图,,即为所求作;
(2)如图,,即为所求作;
(3)∵与的位似比为1:2,
∴∽,,
∴,
∵的面积为3.5平方单位,即的面积为3.5平方单位,
∴的面积为:2=4×3.5=14平方单位.
22.解:(1)△DEF如图所示.
(2)由(1)得:(x,y)经过变换后对应的点的坐标为:(x,y)
(3)由题意得:DE=1,EF=,DF=,
∴△DEF的周长是DE+EF+DF=1++.
23.解:(1)①当放大后的图形在左侧时,画图如下:
②当放大后的图形在右侧时,画图如下:
(2),
或,
即或,
故答案为:或,或;
(3),
或,
故答案为:或
一、选择题
1.下列每组的两个图形中,不是位似图形的是( )
A. B. C. D.
2.如图,点是正三角形的中心,分别是的中点,则与是位似三角形,此时与的位似中心是( )
A.点O B.点P C.点 D.点Q
3.下列四边形和四边形是位似图形,它们的位似中心是( )
A.点E B.点F C.点G D.点D
4.如图,以点O为位似中心,把的各边长放大为原来的2倍得到,以下说法中错误的是( )
A. B.点在同一直线上
C. D.
5.如图,△ABC与△DEF是位似图形,点O为位似中心,已知BO:OE=2:1,则△ABC与△DEF的面积比是
( )
A.2:1 B.3:1 C.4:1 D.5:1
6.如图,已知△ABC与△DEF位似,位似中心为点O,OA:OD=1:3,且△ABC的周长为2,则△DEF的周长为( )
A.4 B.6 C.8 D.18
7.如图,在平面直角坐标系中,以点O为位似中心,将放大得到,点C、D的坐标分别为(2,1)、(2,0),且与的面积之比为1:4,则点A的坐标为( )
A.(8,4) B.(8,2) C.(4,2) D.(4,8)
8.如图,在平面直角坐标系中,与是以点为位似中心的位似图形,且相似比为1:2,点在轴上,若点的坐标是,点的坐标是,则点的坐标是( ).
A. B. C. D.
9.如图,在和是以点为位似中心的位似三角形,若为的中点,,则的长为( )
A. B. C. D.
10.如图,点,是双曲线图象上的两点,连接,线段经过点,点为双曲线在第二象限的分支上一点,当满足且时,的值为( ).
A. B. C. D.
二、填空题
11.在平面直角坐标系中,△ABC中点A的坐标是(2,3),以原点O为位似中心把△ABC放大,使放大后的三角形与△ABC的相似比为3:1,则点A的对应点A′的坐标为_____.
12.如图,已知矩形OABC的面积为27,以O为位似中心,作矩形OABC的位似图形OEDF,使矩形OABC与矩形OEDF的位似比为3:2,若双曲线y=恰好经过点D,则k的值为_____.
13.如图,已知△ABC和△EDC是以点C为位似中心的位似图形,且△ABC和△EDC的位似比为1:2,△ABC面积为4,则△EDC的面积是_____.
14.如图,四边形ABCD与四边形EFGH位似为点O,且=,则=_____.
15.如图,四边形与四边形位似,位似中心点是,,则________.
三、解答题
16.如图,在中,点、、分别是边、、的中点,与是否位似?如果位似,找出位似中心?
17.如图,的三条边与的三条边满足,,,且.的面积与的面积之间有什么关系?
18.如图,在△ABC中,AD,BE分别是BC,AC边上的高.
(1)求证:;
(2)连接DE,那么△CDE与△CAB是位似图形吗?
19.如图,已知B′C′∥BC,C′D′∥CD,D′E′∥DE.
(1)求证:四边形BCDE位似于四边形B′C′D′E′;
(2)若=3,S四边形BCDE=20,求S四边形B′C′D′E′.
20.如果两个一次函数y=k1x+b1和y=k2x+b2满足k1=k2,b1≠b2,那么称这两个一次函数为“平行一次函数”.如图,已知函数y=-2x+4的图象与x轴、y轴分别交于A、B两点,一次函数y=kx+b与y=-2x+4是“平行一次函数”
(1)若函数y=kx+b的图象过点(3,1),求b的值;
(2)若函数y=kx+b的图象与两坐标轴围成的三角形和△AOB构成位似图形,位似中心为原点,位似比为1:2,求函数y=kx+b的表达式.
21.如图,在带有网格的平面直角坐标系中,网格边长为一个单位长度,给出了三角形ABC.
(1)作出关于x轴对称的;
(2)以坐标原点为位似中心在图中的网格中作出的位似图形,使与的位似比为1:2;
(3)若的面积为3.5平方单位,求出的面积.
22.在平面直角坐标系中,△ABC的位置如图所示,每个小正方形的边长为1,以原点O为位似中心,在第一象限内,对△ABC进行位似变换,得到△DEF(点A,B,C分别对应点D,E,F),且△ABC与△DEF的相似比为2:1
(1)画出△DEF;
(2)线段AC上一点(x,y)经过变换后对应的点的坐标为________;
(3)求△DEF的周长.
23.如图,已知O是坐标原点,A,B两点的坐标分别为(2,1),(3,﹣1),
(1)以点O为位似中心,将△OAB放大为原来的两倍,画出图形;
(2)A点的对应点A'的坐标是 ;B点的对应点B′的坐标是 ;
(3)在AB上有一点P(x,y),按(1)的方式得到的对应点P′的坐标是 .
【参考答案】
1.B 2.A 3.D 4.A 5.C 6.B 7.C 8.C 9.B 10.B
11.或
12.12
13.16
14.
15..
16.与是位似图形,位似中心是点,
理由:∵点、、分别是边、、的中点,
∴,
∴,
∵连接、、交于一点,
故与是位似图形.
17.解:的面积为的面积的9倍.
证明:∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴
∴,
∴,
∴,且相似比为3,
∴与的面积比为9.
18.解:(1)证明:、是高,
,
,
,
;
(2)解:如图,
∵△CDE与△CAB不一定是相似三有形,
∴与不是位似图形.
19.(1)∵B′C′∥BC,C′D′∥CD,D′E′∥DE,
∴,
又∵四边形B′C′D′E′和BCDE中对应顶点的连线相交于点A,
∴四边形B′C′D′E′和BCDE是位似图形;
(2)∵,
∴,
又∵四边形B′C′D′E′和BCDE是位似图形,
∴四边形B′C′D′E′和BCDE的相似比为,
∴S四边形B′C′D′E′:S四边形BCDE=9:16,
又∵S四边形BCDE=20,
∴S四边形B′C′D′E′=.
20.(1)由已知得:k=﹣2,把点(3,1)和k=﹣2代入y=kx+b中得:1=﹣2×3+b,∴b=7;
(2)根据位似比为1:2得:函数y=kx+b的图象有两种情况:
①不经过第三象限时,过(1,0)和(0,2),这时表达示为:y=﹣2x+2;
②不经过第一象限时,过(﹣1,0)和(0,﹣2),这时表达示为:y=﹣2x﹣2;
21.解:(1)如图,,即为所求作;
(2)如图,,即为所求作;
(3)∵与的位似比为1:2,
∴∽,,
∴,
∵的面积为3.5平方单位,即的面积为3.5平方单位,
∴的面积为:2=4×3.5=14平方单位.
22.解:(1)△DEF如图所示.
(2)由(1)得:(x,y)经过变换后对应的点的坐标为:(x,y)
(3)由题意得:DE=1,EF=,DF=,
∴△DEF的周长是DE+EF+DF=1++.
23.解:(1)①当放大后的图形在左侧时,画图如下:
②当放大后的图形在右侧时,画图如下:
(2),
或,
即或,
故答案为:或,或;
(3),
或,
故答案为:或
