2021-2022学年苏科版七年级数学下册7.2探索平行线的性质同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册7.2探索平行线的性质同步练习题(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 267.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 00:00:00 | ||
图片预览




文档简介
2021-2022学年苏科版七年级数学下册《7-2探索平行线的性质》同步练习题(附答案)
1.将含30°角的直角三角尺如图摆放,直线a∥b,若∠1=65°,则∠2的度数为( )
A.45° B.50° C.55° D.60°
2.如图所示,若AB∥DE,且∠E=55°,则∠B+∠C的度数是( )
A.135° B.125° C.55° D.45°
3.直线AB∥CD,在AB上任选一点E,将一直角三角板直角顶点放在E处,∠G=30°,当∠AEF=70°,此时∠CHF的大小是( )
A.5° B.10° C.15° D.20°
4.在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2
B.如图3,测得∠1=∠2
C.如图2,展开后测得∠1=∠2且∠3=∠4
D.在图4,展开后测得∠1+∠2=180°
5.如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A.∠1+∠2﹣∠3=90° B.∠1﹣∠2+∠3=90°
C.∠1+∠2+∠3=90° D.∠2+∠3﹣∠1=180°
6.“浏阳河弯过九道弯,五十里水路到湘江.”如图所示,某段河水流经B,C,D三点拐弯后与原来流向相同,若∠ABC=120°,∠BCD=80°,则∠EDC= .
7.如图,图①是长方形纸带,∠DEF=25°,将纸带沿EF折叠成图②,则图②中的∠CFG的度数是 .
8.如图,把一张长方形纸片ABCD沿EF折叠后,点D、C分别落在D'、C'的位置上,若∠EFB=65°,则∠AED'= °.
9.如图,AB∥CD,AE⊥CE,∠EAF=∠EAB,∠ECF=∠ECD.
(1)当a=2时,∠AFC= ;
(2)当a=3时,∠AFC= .
10.某段铁路两旁安置了两座可旋转探照灯,主道路是平行,即PQ∥MN.如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动 秒,两灯的光束互相平行.
11.如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ( ),
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).
12.如图,已知CF∥AG,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠2=58°.
(1)求∠ACE的度数;
(2)若∠1=32°,说明:AB∥CD.
13.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是过点P作PE∥AB,通过平行线的性质来求∠APC.
(1)按照小明的思路,则∠APC的度数为 .
(2)问题迁移:如图2,AB∥CD,点P在射线ON上运动,记∠PAB=α,∠PCD=β.当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P不在B、D两点之间运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
如图,已知AB∥CD,P是直线AB,CD间的一点,PF⊥CD于点F,PE交AB于点E,∠FPE=120°
(1)∠AEP的度数为 .
(2)如图2,射线PN从PF出发,以每秒40°的速度绕P点按逆时针方向旋转,当PN垂直AB时,立刻按原速返回至PF后停止运动;射线EM从EA出发,以每秒15°的速度绕E点按逆时针方向旋转至EB后停止运动.若射线PN,射线EM同时开始运动,设运动时间为t秒.
①当∠MEP=20°时,求∠EPN的度数;
②当EM∥PN时,求t的值.
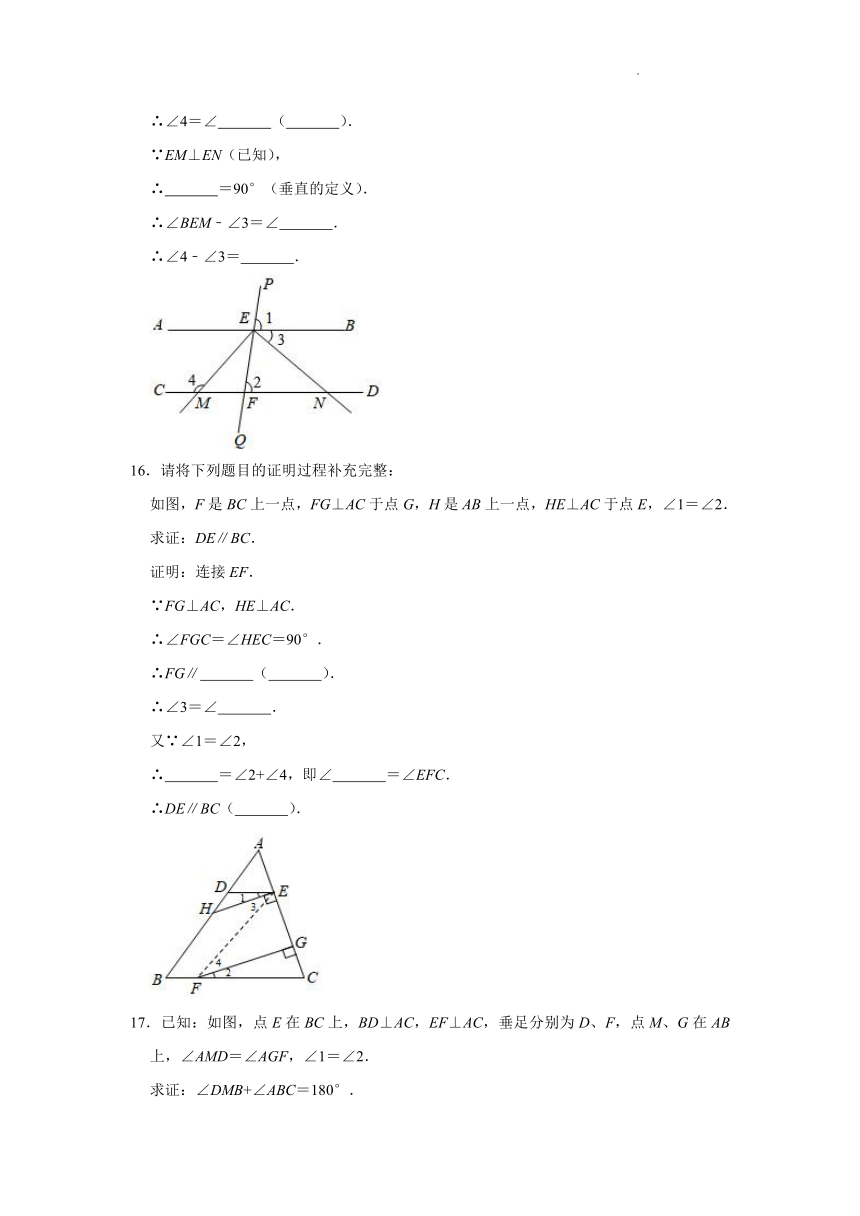
15.完成证明并写出推理根据:如图,直线PQ分别与直线AB、CD交于点E和点F.∠1=∠2,射线EM、EN分别与直线CD交于点M、N,且EM⊥EN,则∠4与∠3有何数量关系?并说明理由.
解:∠4与∠3的数量关系为 ,理由如下:
∵∠1=∠2(已知).
∴AB∥ ( ).
∴∠4=∠ ( ).
∵EM⊥EN(已知),
∴ =90°(垂直的定义).
∴∠BEM﹣∠3=∠ .
∴∠4﹣∠3= .
16.请将下列题目的证明过程补充完整:
如图,F是BC上一点,FG⊥AC于点G,H是AB上一点,HE⊥AC于点E,∠1=∠2.
求证:DE∥BC.
证明:连接EF.
∵FG⊥AC,HE⊥AC.
∴∠FGC=∠HEC=90°.
∴FG∥ ( ).
∴∠3=∠ .
又∵∠1=∠2,
∴ =∠2+∠4,即∠ =∠EFC.
∴DE∥BC( ).
17.已知:如图,点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D、F,点M、G在AB上,∠AMD=∠AGF,∠1=∠2.
求证:∠DMB+∠ABC=180°.
小勇在做上面这道题时用了以下推理过程.请帮他在横线上填写结论,在括号内填写推理依据.
证明:∵BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
∴∠BDC=90°,∠EFC=90° ( ).
∴∠BDC=∠EFC(等量代换).
∴ (同位角相等,两直线平行).
∴∠CBD=∠2 .
∵∠1=∠2(已知).
∴∠CBD=∠1 ( ).
∴ ( ).
∵∠AMD=∠AGF(已知).
∴GF∥MD(同位角相等,两直线平行).
∴BC∥MD ( ).
∴∠DMB+∠ABC=180° ( ).
18.如图,已知点A在EF上,点P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ.
(1)求证:EF∥BC;
(2)若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.
19.问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于 (用含α的式子表示).
20.已知,AB∥CD,试解决下列问题:
(1)如图1,∠1+∠2= ;
(2)如图2,∠1+∠2+∠3= ;
(3)如图3,∠1+∠2+∠3+∠4= ;
(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n= .
参考答案
1.解:如图所示:
∵a∥b,
∴∠3+∠4+∠1=180°,
∵∠4=60°,∠1=65°,
∴∠3=180°﹣∠4﹣∠1=180°﹣60°﹣65°=55°.
故选:C.
2.解:∵AB∥DE,
∴∠E=∠BFE=55°,
∵∠BFE=∠B+∠C,
∴∠B+∠C=55°,
故选:C.
3.解:过G作GM∥AB,则∠MGE=∠BEG,
∵∠AEF=70°,∠FEG=90°,
∴∠BEG=180°﹣90°﹣70°=20°,
∴∠MGE=20°,
∵∠EGF=30°,
∴∠MGF=10°,
∵AB∥CD,
∴MG∥CD,
∴∠CHF=∠MGF=10°,
故选:B.
4.解:A、当∠1=∠2时,a∥b,故此选项不符合题意;
B、∠1=∠2不能判定a,b互相平行,故此选项符合题意;
C、由∠1=∠2且∠3=∠4可得∠1=∠2=∠3=∠4=90°,∴a∥b,故此选项不符合题意;
D、由∠1+∠2=180°可知a∥b,故此选项不符合题意;
故选:B.
5.解:
∵AB∥EF,
∴∠2+∠BOE=180°,
∴∠BOE=180°﹣∠2,同理可得∠COF=180°﹣∠3,
∵O在EF上,
∴∠BOE+∠1+∠COF=180°,
∴180°﹣∠2+∠1+180°﹣∠3=180°,
即∠2+∠3﹣∠1=180°,
故选:D.
6.解:由题意得,AB∥DE,
过点C作CF∥AB,则CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为:20°.
7.解:∵∠DEF=25°,将纸带沿EF折叠成图②,
∴∠FEG=∠DEF=25°,
∵AD∥BC,
∴∠EGB=25°+25°=50°,
∵DE∥CF,
∴∠CFG=130°.
故答案为:130°.
8.解:由题意知AD∥BC,∠EFB=65°,
∴∠DEF=∠EFB=65°,
根据折叠变换的性质知∠D′EF=∠DEF=65°,
则∠AED′=180°﹣∠DEF﹣∠D′EF=50°,
故答案为:50.
9.解:(1)如图,连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=2x°,∠ECD=2y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+2x°+∠ACE+2y°=180°,
∴∠CAE+∠ACE=180°﹣(2x°+2y°),∠FAC+∠FCA=180°﹣(x°+y°),
∵∠AFC+∠FAC+∠FCA=180°,
∴∠AFC=x°+y°,
∵AE⊥CE,
∴∠CAE+∠ACE=90°,
∴180°﹣(2x°+2y°)=90°,
∴x°+y°=45°,
∴∠AFC=45°;
故答案为:45°;
(2)设∠EAF=x°,∠ECF=y°,∠EAB=3x°,∠ECD=3y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+3x°+∠ACE+3y°=180°,
∴∠CAE+∠ACE=180°﹣(3x°+3y°),∠FAC+∠FCA=180°﹣(2x°+2y°),
∴∠AFC=180°﹣(∠FAC+∠FCA)
=180°﹣[180°﹣(2x°+2y°)]
=2x°+2y°
=2(x°+y°),
∵AE⊥CE,
∴∠CAE+∠ACE=90°,
∴180°﹣(3x°+3y°)=90°,
∴x°+y°=30°,
∴∠AFC=2(x°+y°)=60°.
故答案为:60°.
10.解:设A灯转动t秒,两灯的光束互相平行,
①当0<t<90时,如图1,
∵PQ∥MN,
∴∠PBD=∠BDA,
∵AC∥BD,
∴∠CAM=∠BDA,
∴∠CAM=∠PBD,
∴2t=1 (30+t),
解得 t=30;
②当90<t<150时,如图2,
∵PQ∥MN,
∴∠PBD+∠BDA=180°,
∵AC∥BD,
∴∠CAN=∠BDA,
∴∠PBD+∠CAN=180°,
∴1 (30+t)+(2t﹣180)=180,
解得 t=110,
综上所述,当t=30秒或110秒时,两灯的光束互相平行.
11.解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90°(垂直的定义),
∴EF∥AD (同位角相等两直线平行),
∴∠1+∠2=180°(两直线平行同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3 (同角的补角相等),
∴AB∥DG(内错角相等两直线平行),
∴∠GDC=∠B (两直线平行同位角相等).
故答案为:垂直的定义,同位角相等两直线平行,∠1,两直线平行同旁内角互补,同角的补角相等,DG,内错角相等两直线平行,两直线平行同位角相等.
12.解:(1)∵CF∥AG,
∴∠FCH=∠2=58°,
∵CF⊥CE,
∴∠FCE=90°,
∴∠ACE=90°﹣58°=32°;
(2)当∠1=32°时,AB∥CD,理由如下:
∵CE平分∠ACD,
∴∠DCE=∠ACE=32°,
∵∠1=32°,
∴∠1=∠DCE,
∴AB∥CD.
13.解:(1)∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
故答案为:110°;
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.
14.解:(1)延长FP与AB相交于点G,如图1,
∵PF⊥CD,
∴∠PFD=∠PGE=90°,
∵∠EPF=∠PGE+∠AEP,
∴∠AEP=∠EPF﹣∠PGE=120°﹣90°=30°,
故答案为:30°;
(2)①Ⅰ如图2,
∵∠AEP=30°,∠MEP=20°,
∴∠AEM=10°,
∴射线EM运动的时间t==(秒),
∴射线PN旋转的角度∠FPN=×40°=,
又∵∠EPF=120°,
∴∠EPN=∠EPF﹣∠FPN=120°﹣=;
Ⅱ如图3所示,
∵∠AEP=30°,∠MEP=20°,
∴∠AEM=50°,
∴射线EM运动的时间t==(秒),
∴射线PN旋转的角度∠FPN=×40°=,
又∵∠EPF=120°,
∴∠EPN=∠FPN﹣∠EPF=﹣120°=;
∴∠EPN的度数为或;
②Ⅰ当PN由PF运动如图4时EM∥PN,PN与AB相交于点H,
根据题意可知,经过t秒,
∠AEM=15t°,∠FPN=40t°,
∵EM∥PN,
∴∠AEM=∠AHP=15t°,
∴40t°=90°+15t°,
解得t=(秒);
Ⅱ当PN运动到PG,再由PG运动到如图5时EM∥PN,PN与AB相交于点H,
根据题意可知,经过t秒,
∠AEM=15t°,
∵EM∥PN,
∴∠GHP=15t°,∠GPH=90°﹣15t°,
∴PN运动的度数为,180°+∠GPH=40t°,即180°+90°﹣15t°=40t°,
解得t=;
Ⅲ当PN由PG运动如图6时,EM∥PN,
根据题意可知,经过t秒,
∠AEM=15t°,∠GPN=40(t﹣)°=40(t﹣)°,
∵∠AEP=30°,∠EPG=60°,
∴∠PEM=15t°﹣30°,∠EPN=40(t﹣)°﹣60°,
又∵EM∥PN,
∴∠PEM+∠EPN=180°,
∴15t°﹣30°+40(t﹣)°﹣60°=180°,
解得t=(秒),
∴当t的值为秒或秒或秒时,EM∥PN.
15.解:∠4与∠3的数量关系为∠4﹣∠3=90°,理由如下:
∵∠1=∠2(已知),
∴AB∥CD (同位角相等,两直线平行).
∴∠4=∠BEM (两直线平行,内错角相等).
∵EM⊥EN(已知),
∴∠MEN=90° (垂直的定义).
∵∠BEM﹣∠3=∠MEN,
∴∠4﹣∠3=90°.
故答案为:∠4﹣∠3=90°;CD;同位角相等,两直线平行;BEM;两直线平行,内错角相等;∠MEN;MEN;90°.
16.证明:连接EF.
∵FG⊥AC,HE⊥AC.
∴∠FGC=∠HEC=90°.
∴FG∥HE(同位角相等,两直线平行).
∴∠3=∠4.
又∵∠1=∠2,
∴∠1+∠3=∠2+∠4,即∠DEF=∠EFC.
∴DE∥BC(内错角相等,两直线平行).
故答案为:HE,同位角相等,两直线平行;4,∠1+∠3,DEF,内错角相等,两直线平行.
17.证明:∵BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
∴∠BDC=90°,∠EFC=90°( 垂直的定义 ),
∴∠BDC=∠EFC(等量代换),
∴BD∥EF(同位角相等,两直线平行),
∴∠CBD=∠2( 两直线平行,同位角相等 ),
∵∠1=∠2(已知),
∴∠CBD=∠1(等量代换),
∴GF∥BC(内错角相等,两直线平行 ),
∵∠AMD=∠AGF(已知),
∴GF∥MD(同位角相等,两直线平行),
∴BC∥MD(平行公理的推论),
∴∠DMB+∠ABC=180°(两直线平行,同旁内角互补),
故答案为:垂直的定义,BD∥EF,两直线平行,同位角相等,等量代换,GF∥BC,内错角相等,两直线平行,平行公理的推论,两直线平行,同旁内角互补.
18.(1)证明:∵∠E=∠EMA,∠BQM=∠BMQ,∠EMA=∠BMQ,
∴∠E=∠BQM,
∴EF∥BC;
(2)解:∵∠3+∠4=180°,∠4=∠MNF,
∴∠3+∠MNF=180°,
∴AB∥FP,
∴∠F+∠BAF=180°,
∵∠BAF=3∠F﹣20°,
∴∠F+3∠F﹣20°=180°,
解得∠F=50°,
∵AB∥FP,EF∥BC,
∴∠B=∠1,∠1=∠F,
∴∠B=∠F=50°.
19.解:(1)如图1,∵AB∥CD,
∴∠1=∠EGD,
又∵∠2=2∠1,
∴∠2=2∠EGD,
又∵∠FGE=60°,
∴∠EGD=(180°﹣60°)=40°,
∴∠1=40°;
(2)如图2,∵AB∥CD,
∴∠AEG+∠CGE=180°,
即∠AEF+∠FEG+∠EGF+∠FGC=180°,
又∵∠FEG+∠EGF=90°,
∴∠AEF+∠FGC=90°;
(3)如图3,∵AB∥CD,
∴∠AEF+∠CFE=180°,
即∠AEG+∠FEG+∠EFG+∠GFC=180°,
又∵∠GFE=90°,∠GEF=30°,∠AEG=α,
∴∠GFC=180°﹣90°﹣30°﹣α=60°﹣α.
故答案为:60°﹣α.
20.解:(1)∵AB∥CD,∴∠1+∠2=180°(两直线平行,同旁内角互补);
(2)过点E作一条直线EF∥AB,
∵AB∥CD,
∴CD∥EF,
∴∠1+∠AEF=180°,∠FEC+∠3=180°,
∴∠1+∠2+∠3=360°;
(3)过点E、F作EG、FH平行于AB,
∵AB∥CD,
∴AB∥EG∥FH∥CD,
∴∠1+∠AEG=180°,∠GEF+∠EFH=180°,∠HFC+∠4=180°;
∴∠1+∠2+∠3+∠4=540°;
(4)根据上述规律,显然作(n﹣2)条辅助线,运用(n﹣1)次两条直线平行,同旁内角互补.即可得到n个角的和是180°(n﹣1).
1.将含30°角的直角三角尺如图摆放,直线a∥b,若∠1=65°,则∠2的度数为( )
A.45° B.50° C.55° D.60°
2.如图所示,若AB∥DE,且∠E=55°,则∠B+∠C的度数是( )
A.135° B.125° C.55° D.45°
3.直线AB∥CD,在AB上任选一点E,将一直角三角板直角顶点放在E处,∠G=30°,当∠AEF=70°,此时∠CHF的大小是( )
A.5° B.10° C.15° D.20°
4.在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
A.如图1,展开后测得∠1=∠2
B.如图3,测得∠1=∠2
C.如图2,展开后测得∠1=∠2且∠3=∠4
D.在图4,展开后测得∠1+∠2=180°
5.如图,如果AB∥EF,EF∥CD,下列各式正确的是( )
A.∠1+∠2﹣∠3=90° B.∠1﹣∠2+∠3=90°
C.∠1+∠2+∠3=90° D.∠2+∠3﹣∠1=180°
6.“浏阳河弯过九道弯,五十里水路到湘江.”如图所示,某段河水流经B,C,D三点拐弯后与原来流向相同,若∠ABC=120°,∠BCD=80°,则∠EDC= .
7.如图,图①是长方形纸带,∠DEF=25°,将纸带沿EF折叠成图②,则图②中的∠CFG的度数是 .
8.如图,把一张长方形纸片ABCD沿EF折叠后,点D、C分别落在D'、C'的位置上,若∠EFB=65°,则∠AED'= °.
9.如图,AB∥CD,AE⊥CE,∠EAF=∠EAB,∠ECF=∠ECD.
(1)当a=2时,∠AFC= ;
(2)当a=3时,∠AFC= .
10.某段铁路两旁安置了两座可旋转探照灯,主道路是平行,即PQ∥MN.如图所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动 秒,两灯的光束互相平行.
11.如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.请补充说明过程,并在括号内填上相应的理由.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ( ),
∴EF∥AD( ),
∴ +∠2=180°( ).
又∵∠2+∠3=180°(已知),
∴∠1=∠3( ),
∴AB∥ ( ),
∴∠GDC=∠B( ).
12.如图,已知CF∥AG,E是直线AB上的一点,CE平分∠ACD,射线CF⊥CE,∠2=58°.
(1)求∠ACE的度数;
(2)若∠1=32°,说明:AB∥CD.
13.问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是过点P作PE∥AB,通过平行线的性质来求∠APC.
(1)按照小明的思路,则∠APC的度数为 .
(2)问题迁移:如图2,AB∥CD,点P在射线ON上运动,记∠PAB=α,∠PCD=β.当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P不在B、D两点之间运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.
如图,已知AB∥CD,P是直线AB,CD间的一点,PF⊥CD于点F,PE交AB于点E,∠FPE=120°
(1)∠AEP的度数为 .
(2)如图2,射线PN从PF出发,以每秒40°的速度绕P点按逆时针方向旋转,当PN垂直AB时,立刻按原速返回至PF后停止运动;射线EM从EA出发,以每秒15°的速度绕E点按逆时针方向旋转至EB后停止运动.若射线PN,射线EM同时开始运动,设运动时间为t秒.
①当∠MEP=20°时,求∠EPN的度数;
②当EM∥PN时,求t的值.
15.完成证明并写出推理根据:如图,直线PQ分别与直线AB、CD交于点E和点F.∠1=∠2,射线EM、EN分别与直线CD交于点M、N,且EM⊥EN,则∠4与∠3有何数量关系?并说明理由.
解:∠4与∠3的数量关系为 ,理由如下:
∵∠1=∠2(已知).
∴AB∥ ( ).
∴∠4=∠ ( ).
∵EM⊥EN(已知),
∴ =90°(垂直的定义).
∴∠BEM﹣∠3=∠ .
∴∠4﹣∠3= .
16.请将下列题目的证明过程补充完整:
如图,F是BC上一点,FG⊥AC于点G,H是AB上一点,HE⊥AC于点E,∠1=∠2.
求证:DE∥BC.
证明:连接EF.
∵FG⊥AC,HE⊥AC.
∴∠FGC=∠HEC=90°.
∴FG∥ ( ).
∴∠3=∠ .
又∵∠1=∠2,
∴ =∠2+∠4,即∠ =∠EFC.
∴DE∥BC( ).
17.已知:如图,点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D、F,点M、G在AB上,∠AMD=∠AGF,∠1=∠2.
求证:∠DMB+∠ABC=180°.
小勇在做上面这道题时用了以下推理过程.请帮他在横线上填写结论,在括号内填写推理依据.
证明:∵BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
∴∠BDC=90°,∠EFC=90° ( ).
∴∠BDC=∠EFC(等量代换).
∴ (同位角相等,两直线平行).
∴∠CBD=∠2 .
∵∠1=∠2(已知).
∴∠CBD=∠1 ( ).
∴ ( ).
∵∠AMD=∠AGF(已知).
∴GF∥MD(同位角相等,两直线平行).
∴BC∥MD ( ).
∴∠DMB+∠ABC=180° ( ).
18.如图,已知点A在EF上,点P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ.
(1)求证:EF∥BC;
(2)若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.
19.问题情境
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于 (用含α的式子表示).
20.已知,AB∥CD,试解决下列问题:
(1)如图1,∠1+∠2= ;
(2)如图2,∠1+∠2+∠3= ;
(3)如图3,∠1+∠2+∠3+∠4= ;
(4)如图4,试探究∠1+∠2+∠3+∠4+…+∠n= .
参考答案
1.解:如图所示:
∵a∥b,
∴∠3+∠4+∠1=180°,
∵∠4=60°,∠1=65°,
∴∠3=180°﹣∠4﹣∠1=180°﹣60°﹣65°=55°.
故选:C.
2.解:∵AB∥DE,
∴∠E=∠BFE=55°,
∵∠BFE=∠B+∠C,
∴∠B+∠C=55°,
故选:C.
3.解:过G作GM∥AB,则∠MGE=∠BEG,
∵∠AEF=70°,∠FEG=90°,
∴∠BEG=180°﹣90°﹣70°=20°,
∴∠MGE=20°,
∵∠EGF=30°,
∴∠MGF=10°,
∵AB∥CD,
∴MG∥CD,
∴∠CHF=∠MGF=10°,
故选:B.
4.解:A、当∠1=∠2时,a∥b,故此选项不符合题意;
B、∠1=∠2不能判定a,b互相平行,故此选项符合题意;
C、由∠1=∠2且∠3=∠4可得∠1=∠2=∠3=∠4=90°,∴a∥b,故此选项不符合题意;
D、由∠1+∠2=180°可知a∥b,故此选项不符合题意;
故选:B.
5.解:
∵AB∥EF,
∴∠2+∠BOE=180°,
∴∠BOE=180°﹣∠2,同理可得∠COF=180°﹣∠3,
∵O在EF上,
∴∠BOE+∠1+∠COF=180°,
∴180°﹣∠2+∠1+180°﹣∠3=180°,
即∠2+∠3﹣∠1=180°,
故选:D.
6.解:由题意得,AB∥DE,
过点C作CF∥AB,则CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为:20°.
7.解:∵∠DEF=25°,将纸带沿EF折叠成图②,
∴∠FEG=∠DEF=25°,
∵AD∥BC,
∴∠EGB=25°+25°=50°,
∵DE∥CF,
∴∠CFG=130°.
故答案为:130°.
8.解:由题意知AD∥BC,∠EFB=65°,
∴∠DEF=∠EFB=65°,
根据折叠变换的性质知∠D′EF=∠DEF=65°,
则∠AED′=180°﹣∠DEF﹣∠D′EF=50°,
故答案为:50.
9.解:(1)如图,连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=2x°,∠ECD=2y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+2x°+∠ACE+2y°=180°,
∴∠CAE+∠ACE=180°﹣(2x°+2y°),∠FAC+∠FCA=180°﹣(x°+y°),
∵∠AFC+∠FAC+∠FCA=180°,
∴∠AFC=x°+y°,
∵AE⊥CE,
∴∠CAE+∠ACE=90°,
∴180°﹣(2x°+2y°)=90°,
∴x°+y°=45°,
∴∠AFC=45°;
故答案为:45°;
(2)设∠EAF=x°,∠ECF=y°,∠EAB=3x°,∠ECD=3y°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠CAE+3x°+∠ACE+3y°=180°,
∴∠CAE+∠ACE=180°﹣(3x°+3y°),∠FAC+∠FCA=180°﹣(2x°+2y°),
∴∠AFC=180°﹣(∠FAC+∠FCA)
=180°﹣[180°﹣(2x°+2y°)]
=2x°+2y°
=2(x°+y°),
∵AE⊥CE,
∴∠CAE+∠ACE=90°,
∴180°﹣(3x°+3y°)=90°,
∴x°+y°=30°,
∴∠AFC=2(x°+y°)=60°.
故答案为:60°.
10.解:设A灯转动t秒,两灯的光束互相平行,
①当0<t<90时,如图1,
∵PQ∥MN,
∴∠PBD=∠BDA,
∵AC∥BD,
∴∠CAM=∠BDA,
∴∠CAM=∠PBD,
∴2t=1 (30+t),
解得 t=30;
②当90<t<150时,如图2,
∵PQ∥MN,
∴∠PBD+∠BDA=180°,
∵AC∥BD,
∴∠CAN=∠BDA,
∴∠PBD+∠CAN=180°,
∴1 (30+t)+(2t﹣180)=180,
解得 t=110,
综上所述,当t=30秒或110秒时,两灯的光束互相平行.
11.解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90°(垂直的定义),
∴EF∥AD (同位角相等两直线平行),
∴∠1+∠2=180°(两直线平行同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3 (同角的补角相等),
∴AB∥DG(内错角相等两直线平行),
∴∠GDC=∠B (两直线平行同位角相等).
故答案为:垂直的定义,同位角相等两直线平行,∠1,两直线平行同旁内角互补,同角的补角相等,DG,内错角相等两直线平行,两直线平行同位角相等.
12.解:(1)∵CF∥AG,
∴∠FCH=∠2=58°,
∵CF⊥CE,
∴∠FCE=90°,
∴∠ACE=90°﹣58°=32°;
(2)当∠1=32°时,AB∥CD,理由如下:
∵CE平分∠ACD,
∴∠DCE=∠ACE=32°,
∵∠1=32°,
∴∠1=∠DCE,
∴AB∥CD.
13.解:(1)∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
故答案为:110°;
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.
14.解:(1)延长FP与AB相交于点G,如图1,
∵PF⊥CD,
∴∠PFD=∠PGE=90°,
∵∠EPF=∠PGE+∠AEP,
∴∠AEP=∠EPF﹣∠PGE=120°﹣90°=30°,
故答案为:30°;
(2)①Ⅰ如图2,
∵∠AEP=30°,∠MEP=20°,
∴∠AEM=10°,
∴射线EM运动的时间t==(秒),
∴射线PN旋转的角度∠FPN=×40°=,
又∵∠EPF=120°,
∴∠EPN=∠EPF﹣∠FPN=120°﹣=;
Ⅱ如图3所示,
∵∠AEP=30°,∠MEP=20°,
∴∠AEM=50°,
∴射线EM运动的时间t==(秒),
∴射线PN旋转的角度∠FPN=×40°=,
又∵∠EPF=120°,
∴∠EPN=∠FPN﹣∠EPF=﹣120°=;
∴∠EPN的度数为或;
②Ⅰ当PN由PF运动如图4时EM∥PN,PN与AB相交于点H,
根据题意可知,经过t秒,
∠AEM=15t°,∠FPN=40t°,
∵EM∥PN,
∴∠AEM=∠AHP=15t°,
∴40t°=90°+15t°,
解得t=(秒);
Ⅱ当PN运动到PG,再由PG运动到如图5时EM∥PN,PN与AB相交于点H,
根据题意可知,经过t秒,
∠AEM=15t°,
∵EM∥PN,
∴∠GHP=15t°,∠GPH=90°﹣15t°,
∴PN运动的度数为,180°+∠GPH=40t°,即180°+90°﹣15t°=40t°,
解得t=;
Ⅲ当PN由PG运动如图6时,EM∥PN,
根据题意可知,经过t秒,
∠AEM=15t°,∠GPN=40(t﹣)°=40(t﹣)°,
∵∠AEP=30°,∠EPG=60°,
∴∠PEM=15t°﹣30°,∠EPN=40(t﹣)°﹣60°,
又∵EM∥PN,
∴∠PEM+∠EPN=180°,
∴15t°﹣30°+40(t﹣)°﹣60°=180°,
解得t=(秒),
∴当t的值为秒或秒或秒时,EM∥PN.
15.解:∠4与∠3的数量关系为∠4﹣∠3=90°,理由如下:
∵∠1=∠2(已知),
∴AB∥CD (同位角相等,两直线平行).
∴∠4=∠BEM (两直线平行,内错角相等).
∵EM⊥EN(已知),
∴∠MEN=90° (垂直的定义).
∵∠BEM﹣∠3=∠MEN,
∴∠4﹣∠3=90°.
故答案为:∠4﹣∠3=90°;CD;同位角相等,两直线平行;BEM;两直线平行,内错角相等;∠MEN;MEN;90°.
16.证明:连接EF.
∵FG⊥AC,HE⊥AC.
∴∠FGC=∠HEC=90°.
∴FG∥HE(同位角相等,两直线平行).
∴∠3=∠4.
又∵∠1=∠2,
∴∠1+∠3=∠2+∠4,即∠DEF=∠EFC.
∴DE∥BC(内错角相等,两直线平行).
故答案为:HE,同位角相等,两直线平行;4,∠1+∠3,DEF,内错角相等,两直线平行.
17.证明:∵BD⊥AC,EF⊥AC,垂足分别为D、F(已知),
∴∠BDC=90°,∠EFC=90°( 垂直的定义 ),
∴∠BDC=∠EFC(等量代换),
∴BD∥EF(同位角相等,两直线平行),
∴∠CBD=∠2( 两直线平行,同位角相等 ),
∵∠1=∠2(已知),
∴∠CBD=∠1(等量代换),
∴GF∥BC(内错角相等,两直线平行 ),
∵∠AMD=∠AGF(已知),
∴GF∥MD(同位角相等,两直线平行),
∴BC∥MD(平行公理的推论),
∴∠DMB+∠ABC=180°(两直线平行,同旁内角互补),
故答案为:垂直的定义,BD∥EF,两直线平行,同位角相等,等量代换,GF∥BC,内错角相等,两直线平行,平行公理的推论,两直线平行,同旁内角互补.
18.(1)证明:∵∠E=∠EMA,∠BQM=∠BMQ,∠EMA=∠BMQ,
∴∠E=∠BQM,
∴EF∥BC;
(2)解:∵∠3+∠4=180°,∠4=∠MNF,
∴∠3+∠MNF=180°,
∴AB∥FP,
∴∠F+∠BAF=180°,
∵∠BAF=3∠F﹣20°,
∴∠F+3∠F﹣20°=180°,
解得∠F=50°,
∵AB∥FP,EF∥BC,
∴∠B=∠1,∠1=∠F,
∴∠B=∠F=50°.
19.解:(1)如图1,∵AB∥CD,
∴∠1=∠EGD,
又∵∠2=2∠1,
∴∠2=2∠EGD,
又∵∠FGE=60°,
∴∠EGD=(180°﹣60°)=40°,
∴∠1=40°;
(2)如图2,∵AB∥CD,
∴∠AEG+∠CGE=180°,
即∠AEF+∠FEG+∠EGF+∠FGC=180°,
又∵∠FEG+∠EGF=90°,
∴∠AEF+∠FGC=90°;
(3)如图3,∵AB∥CD,
∴∠AEF+∠CFE=180°,
即∠AEG+∠FEG+∠EFG+∠GFC=180°,
又∵∠GFE=90°,∠GEF=30°,∠AEG=α,
∴∠GFC=180°﹣90°﹣30°﹣α=60°﹣α.
故答案为:60°﹣α.
20.解:(1)∵AB∥CD,∴∠1+∠2=180°(两直线平行,同旁内角互补);
(2)过点E作一条直线EF∥AB,
∵AB∥CD,
∴CD∥EF,
∴∠1+∠AEF=180°,∠FEC+∠3=180°,
∴∠1+∠2+∠3=360°;
(3)过点E、F作EG、FH平行于AB,
∵AB∥CD,
∴AB∥EG∥FH∥CD,
∴∠1+∠AEG=180°,∠GEF+∠EFH=180°,∠HFC+∠4=180°;
∴∠1+∠2+∠3+∠4=540°;
(4)根据上述规律,显然作(n﹣2)条辅助线,运用(n﹣1)次两条直线平行,同旁内角互补.即可得到n个角的和是180°(n﹣1).
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
