2021-2022学年冀教版七年级数学下册7.5平行线的性质同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版七年级数学下册7.5平行线的性质同步练习题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 230.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 08:41:16 | ||
图片预览




文档简介
2021-2022学年冀教版七年级数学下册《7-5平行线的性质》同步练习题(附答案)
1.如图,∠1=∠2=∠3=56°,则∠4的度数是( )
A.56° B.114° C.124° D.146°
2.如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3=( )
A.36° B.52° C.72° D.80°
3.下列说法:①不相交的两条直线平行;②在同一平面内,两条直线的位置关系有两种;③若直线AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图所示,下列判断正确的个数是( )
①若∠1=∠3,AD∥BC,则BD是∠ABC的平分线;
②若AD∥BC,则∠1=∠2=∠3;
③若∠3+∠4+∠C=180°,则AD∥BC;
④若∠2=∠3,则AD∥BC.
A.1 B.2 C.3 D.4
5.如图,在下列条件中,能使AD∥BC的是( )
A.∠BAC=∠DCA B.∠ABC=∠ADC
C.∠DAC=∠BCA D.∠ABC+∠BCD=180°
6.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个 B.2个 C.1个 D.0个
7.如图,在四边形ABCD中,若∠ABC+∠C=180°,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠2=∠4
8.如图,下列条件:①∠C=∠CAF;②∠C=∠EDB;③∠BAC+∠C=180°;④∠GDE+∠B=180°.其中能判断AB∥CD的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,已知∠BAD=55°,∠1=70°,若∠BAD+∠ADE=180°,则∠2=( )
A.25° B.45° C.55° D.75°
10.如图,直线l分别与直线AB、CD相交于点E、F,EG平分∠BEF交直线CD于点G,若∠1=∠BEF=72°,则∠EGF的度数为( )
A.34° B.36° C.38° D.68°
11.如图,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F=135°,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
12.如图,∠1=80°,∠2=100°,∠3=76°,则∠4的度数为 度.
13.如图,下列推理是否正确,请写出你认为是正确推理的编号 .
①因为AB∥DC,所以∠ABC+∠C=180°
②因为∠1=∠2,所以AD∥BC
③因为AD∥BC,所以∠3=∠4
④因为∠A+∠ADC=180°,所以AB∥DC.
14.如图,AB⊥EF,CD⊥EF,∠1=∠F=45°,那么与∠FCD相等的角有 个,它们分别是 .
15.如图,∠1=∠2,∠3=100°,则∠4= .
16.如图,已知EF⊥AC于点F,DB⊥AC于点M.∠1=∠2,∠3=∠C,若∠ANM=70°,∠BAN的度数是 .
17.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为 度.
18.如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
(1)请直接写出直线AC与DG的位置关系;
(2)求证:BE∥CF;
(3)若∠C=35°,求∠BED的度数.
19.已知AE∥BD,若∠1=∠2,∠3=∠4,求证:ED∥AC.
20.如图,已知∠2=∠4,∠3=∠B.
(1)试判断∠AED与∠C的关系,并说明理由;
(2)若∠1=130°,∠5=65°,求∠DGB的度数.
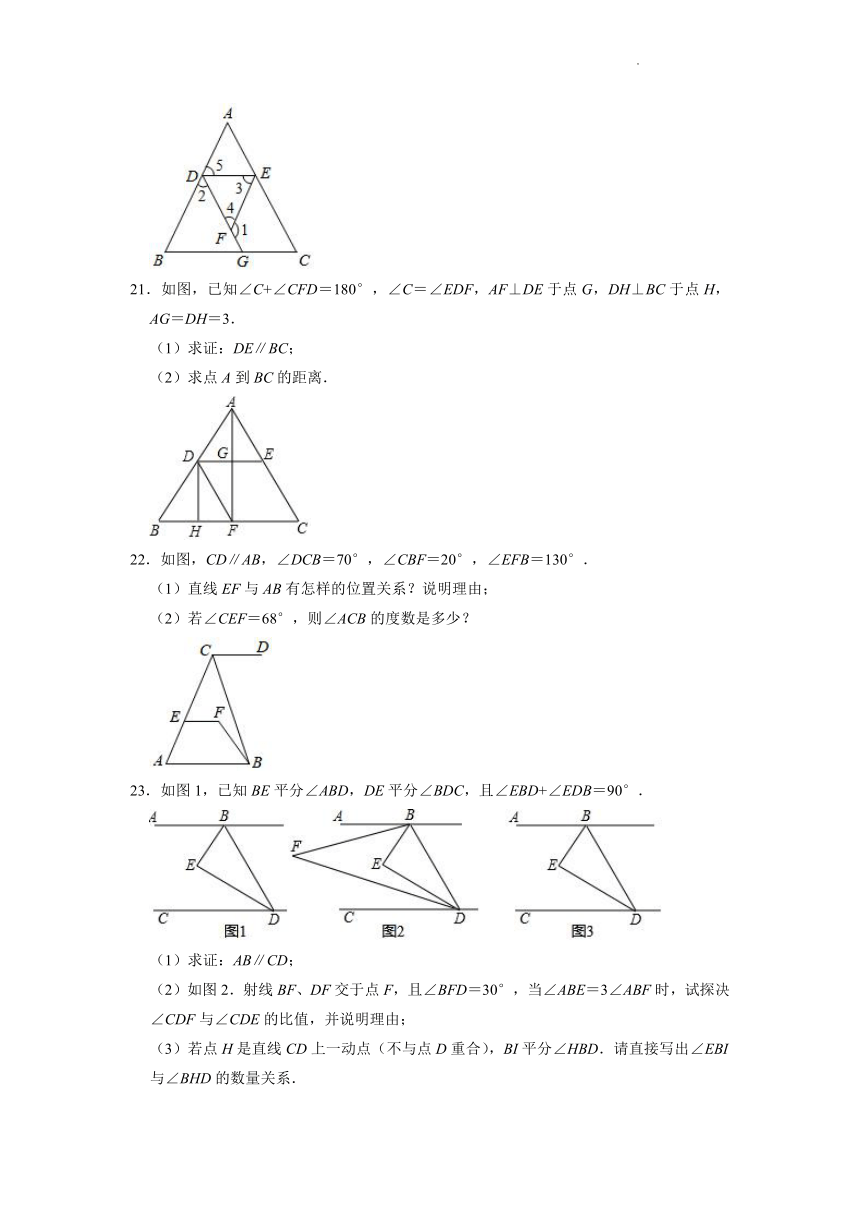
21.如图,已知∠C+∠CFD=180°,∠C=∠EDF,AF⊥DE于点G,DH⊥BC于点H,AG=DH=3.
(1)求证:DE∥BC;
(2)求点A到BC的距离.
22.如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°.
(1)直线EF与AB有怎样的位置关系?说明理由;
(2)若∠CEF=68°,则∠ACB的度数是多少?
23.如图1,已知BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
(1)求证:AB∥CD;
(2)如图2.射线BF、DF交于点F,且∠BFD=30°,当∠ABE=3∠ABF时,试探决∠CDF与∠CDE的比值,并说明理由;
(3)若点H是直线CD上一动点(不与点D重合),BI平分∠HBD.请直接写出∠EBI与∠BHD的数量关系.
24.如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠AEF与∠EFC的角平分线交于点P,EP延长线与CD交于点G,点H是MN上一点,且PF∥GH,试判断直GH与EG的位置关系,并说明理由.
参考答案
1.解:如图,
∵∠1=∠2,∠2=∠5,
∴∠1=∠5,
∴l1∥l2,
∴∠3=∠6,
∵∠3=56°,
∴∠6=56°,
∵∠4+∠6=180°,
∴∠4=180°﹣56°=124°,
故选:C.
2.解:∵∠1=∠2=36°,
∴AC∥DE,
∴∠ACB=∠3,
∵CD平分∠ACB,
∴∠ACB=2∠1=72°,
∴∠3=72°.
故选:C.
3.解:①不相交的两条直线是平行线;此说法错误,应强调在同一平面内;
②在同一平面内,两条直线的位置关系有两种,正确,有相交或平行两种关系;
③若直线AB与CD没有交点,则AB∥CD;此说法错误,应强调在同一平面内;
④若a∥b,b∥c,则a与c不相交;根据平行公理的推论:如果两条直线都和第三条直线平行,那么两条直线也互相平行,上面说法正确.
故说法正确的有2个.
故选:B.
4.解:①∵AD∥BC,
∴∠2=∠3,
∵∠1=∠3,
∴∠1=∠2,
∴BD是∠ABC的平分线,故①正确;
②若AD∥BC,则∠2=∠3,并不能推出∠1与∠2和∠3的关系,故②错误;
③由“同旁内角互补,两直线平行”可知:若∠3+∠4+∠C=180°,则AD∥BC,故③正确;
④由“内错角相等,两直线平行”可知,若∠2=∠3,则AD∥BC,故④正确;
综上,正确的个数是3,
故选:C.
5.解:∠BAC=∠DCA,根据“内错角相等,两直线平行”可判定AB∥CD,不能判定AD∥BC,故A不符合题意;
∠ABC=∠ADC,不能判定AD∥BC,故B不符合题意;
∠DAC=∠BCA,根据“内错角相等,两直线平行”可判定AD∥BC,故C符合题意;
∠ABC+∠BCD=180°,根据“同旁内角互补,两直线平行”可判定AB∥CD,不能判定AD∥BC,故A不符合题意;
故选:C.
6.解:①∵AB⊥BC,DC⊥BC,
∴AB∥CD,
∴∠BAD+∠ADC=180°,
故①正确;
②∵AB∥CD,
∴∠AFD+∠BAF=180°,
∵∠BAF=∠EDF,
∴∠AFD+∠EDF=180°,
∴AF∥DE,
故②正确;
③∵AF∥ED,
∴∠DAF=∠ADE,∠F=∠CDE,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DAF=∠F,
故③正确;
故选:A.
7.解:∵四边形ABCD中∠ABC+∠C=180°,
∴AB∥DC,
∴∠2=∠4.
故选:D.
8.解:∵∠C=∠CAF,
∴AB∥CD,
∵∠BAC+∠C=180°,
∴AB∥CD,
∵∠GDE+∠B=180°,∠GDE+∠EDB=180°,
∴∠EDB=∠B,
∴AB∥CD,
所以能判断AB∥CD的是①∠C=∠CAF,③∠BAC+∠C=180°,④∠GDE+∠B=180°,
故选:C.
9.解:∵∠BAD+∠ADE=180°,
∴AB∥DE.
∴∠CDA=∠BAD=55°.
∵∠1+∠2+∠CDA=180°,
∴∠2=180°﹣∠1﹣∠CDA=180°﹣70°﹣55°=55°.
故选:C.
10.解:∵∠1=∠BEF=72°,
∴AB∥CD.
∴∠EGF=∠GEB.
∵EG平分∠BEF,
∴∠GEB=∠BEF=36°.
∴∠EGF=∠GEB=36°.
故选:B.
11.解:∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°﹣90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°﹣90°=45°,
∴∠F=180°﹣(∠FAD+∠FDA)=180﹣45°=135°,故④正确.
综上所述正确的有:①③④,共3个.
故选:C.
12.解:∵∠1=80°,
∴∠5=100°.
∵∠2=100°,∠3=76°,
∴∠2=∠5,
∴a∥b.
∴∠4=∠3=76°.
故答案为:76.
13.解:①∵AB∥DC,∴∠ABC+∠C=180°,此结论正确;
②∵∠1=∠2,∴AD∥BC,此结论正确;
③∵AD∥BC,∴∠1=∠2,而∠3≠∠4,此结论错误,
④∵∠A+∠ADC=180°,∴AB∥DC,此结论正确.
故答案为①②④.
14.解:与∠FCD相等的角有4个,它们分别是∠1、∠F、∠A、∠ABG.
故答案是:4;∠1、∠F、∠A、∠ABG.
15.解:如图,
∵∠1=∠2,
∴AD∥BC,
∴∠3+∠4=180°,
而∠3=100°,
∴∠4=180°﹣100°=80°.
故答案为80°.
16.解:∵EF⊥AC,DB⊥AC,
∴∠EFC=∠DMC=90°,
∴BD∥FE,
∴∠2=∠BDC,
∵∠1=∠2,
∴∠1=∠BDC,
∴MN∥CD,
∵∠3=∠C,
∴AB∥CD,
∴MN∥AB,
∴∠BAN+∠ANM=180°,
∵∠ANM=70°,
∴∠BAN=110°,
故答案为:110°.
17.解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF=BEF=31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
18.解:(1)AC∥DG,理由如下:
∵∠ABF=∠1,∠1=∠2,
∴∠ABF=∠2,
∴AC∥DG;
(2)由(1)知AC∥DG,
∴∠ABF=∠BFG,
∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,
∴,∠CFB=∠BFG,
∴∠EBF=∠CFB,
∴BE∥CF.
(3)∵AC∥DG,∠C=35°,
∴∠C=∠CFG=35°,
∵BE∥CF,
∴∠CFG=∠BEG=35°,
∴∠BED=180°﹣∠BEG=145°.
19.证明:∵∠DFE=∠2,∠D=180°﹣∠4﹣∠DFE,∠A=180°﹣∠3﹣∠1,
∴∠D=180°﹣∠4﹣∠2,
∴∠A=∠D,
∵AE∥BD,
∴∠A=∠DBC,
∴∠D=∠DBC,
∴ED∥AC.
20.解:(1)∠AED=∠C,理由如下:
∵∠2=∠4,
∴BD∥EF,
∴∠BDE+∠3=180°,
∵∠3=∠B,
∴∠BDE+∠B=180°,
∴DE∥BC,
∴∠AED=∠C;
(2)∵∠1+∠4=180°,∠1=130°,
∴∠4=50°,
∵∠2=∠4,
∴∠2=50°,
∵DE∥BC,
∴∠5=∠B,
∵∠5=65°,
∴∠B=65°,
在△BDG,∠B+∠2+∠DGB=180°,∠B=65°,∠2=50°,
∴∠DGB=65°.
21.(1)证明:∵∠C+∠CFD=180°,∠C=∠EDF,
∴∠EDF+∠CFD=180°,
∴DE∥BC;
(2)解:由(1)知DE∥BC,
∵AF⊥DE,
∴AF⊥BC,
∴AF的长是点A到BC的距离,
∵DH⊥BC,
∴DH∥AF,
∵DE∥BC,
∴四边形DHFG是平行四边形,
∴DH=GF,
∵AG=DH=3,
∴AF=AG+GF=3+3=6.
22.解:(1)EF和AB的位置关系为平行关系.理由如下:
∵CD∥AB,∠DCB=70°,
∴∠DCB=∠ABC=70°,
∵∠CBF=20°,
∴∠ABF=∠ABC﹣∠CBF=50°,
∵∠EFB=130°,
∴∠ABF+∠EFB=50°+130°=180°,
∴EF∥AB;
(2)∵EF∥AB,CD∥AB,
∴EF∥CD,
∵∠CEF=68°,
∴∠ECD=112°,
∵∠DCB=70°,
∴∠ACB=∠ECD﹣∠DCB,
∴∠ACB=42°.
23.证明:(1)∵BE平分∠ABD,DE平分∠BDC,
∴∠ABD=2∠EBD,∠CDB=2∠EDB,
又∵∠EBD+∠EDB=90°,
∴∠ABD+∠CBD=2×90°=180°,
∴AB∥CD;
(2)=,理由如下:
作EP∥AB,FQ∥AB,如图2,
又∵AB∥CD,
∴AB∥CD∥EP,AB∥CD∥FQ,
∴∠ABE=∠BEP,∠DEP=∠CDE,
∴∠BED=∠BEP+∠DEP=∠ABE+∠CDE=90°,
同理,∠BFD=∠ABF+∠CDF,
∵∠ABE=3∠ABF,∠BFD=30°,
∴∠BFD=∠ABE+∠CDF=30°=∠BED,
∴=;
(3)∵BE平分∠ABD,
∴∠ABD=2∠EBD,
∵BI平分∠HBD,
∴∠HBD=2∠IBD,
如图1,点H在点D的左边时,∠ABH=∠ABD﹣∠HBD,∠EBI=∠EBD﹣∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=∠ABH,
∴∠BHD=2∠EBI,
如图2,点H在点D的右边时,∠ABH=∠ABD+∠HBD,
∠EBI=∠EBD+∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=180°﹣∠ABH,
∴∠BHD=180°﹣2∠EBI,
综上所述,∠BHD=2∠EBI或∠BHD=180°﹣2∠EBI.
24.解:(1)AB∥CD,理由如下:
∵∠1与∠2互补,
∴∠1+∠2=180°,
又∵∠2+∠CFE=180°,
∴∠1=∠CFE,
∴AB∥CD;
(2)GH⊥EG,理由如下:
由(1)知,AB∥CD,
∴∠AEF+∠EFC=180°.
又∵∠AEF与∠EFC的角平分线交于点P,
∴∠FEP+∠EFP=(∠BEF+∠EFD)=90°,
∴∠EPF=90°,即EG⊥PF,
∵PF∥GH,
∴GH⊥EG.
1.如图,∠1=∠2=∠3=56°,则∠4的度数是( )
A.56° B.114° C.124° D.146°
2.如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3=( )
A.36° B.52° C.72° D.80°
3.下列说法:①不相交的两条直线平行;②在同一平面内,两条直线的位置关系有两种;③若直线AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
4.如图所示,下列判断正确的个数是( )
①若∠1=∠3,AD∥BC,则BD是∠ABC的平分线;
②若AD∥BC,则∠1=∠2=∠3;
③若∠3+∠4+∠C=180°,则AD∥BC;
④若∠2=∠3,则AD∥BC.
A.1 B.2 C.3 D.4
5.如图,在下列条件中,能使AD∥BC的是( )
A.∠BAC=∠DCA B.∠ABC=∠ADC
C.∠DAC=∠BCA D.∠ABC+∠BCD=180°
6.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有( )
①∠BAD+∠ADC=180°;②AF∥DE;③∠DAF=∠F.
A.3个 B.2个 C.1个 D.0个
7.如图,在四边形ABCD中,若∠ABC+∠C=180°,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠2=∠4
8.如图,下列条件:①∠C=∠CAF;②∠C=∠EDB;③∠BAC+∠C=180°;④∠GDE+∠B=180°.其中能判断AB∥CD的有( )
A.1个 B.2个 C.3个 D.4个
9.如图,已知∠BAD=55°,∠1=70°,若∠BAD+∠ADE=180°,则∠2=( )
A.25° B.45° C.55° D.75°
10.如图,直线l分别与直线AB、CD相交于点E、F,EG平分∠BEF交直线CD于点G,若∠1=∠BEF=72°,则∠EGF的度数为( )
A.34° B.36° C.38° D.68°
11.如图,AB⊥BC,AE平分∠BAD交BC于E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F=135°,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
12.如图,∠1=80°,∠2=100°,∠3=76°,则∠4的度数为 度.
13.如图,下列推理是否正确,请写出你认为是正确推理的编号 .
①因为AB∥DC,所以∠ABC+∠C=180°
②因为∠1=∠2,所以AD∥BC
③因为AD∥BC,所以∠3=∠4
④因为∠A+∠ADC=180°,所以AB∥DC.
14.如图,AB⊥EF,CD⊥EF,∠1=∠F=45°,那么与∠FCD相等的角有 个,它们分别是 .
15.如图,∠1=∠2,∠3=100°,则∠4= .
16.如图,已知EF⊥AC于点F,DB⊥AC于点M.∠1=∠2,∠3=∠C,若∠ANM=70°,∠BAN的度数是 .
17.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为 度.
18.如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
(1)请直接写出直线AC与DG的位置关系;
(2)求证:BE∥CF;
(3)若∠C=35°,求∠BED的度数.
19.已知AE∥BD,若∠1=∠2,∠3=∠4,求证:ED∥AC.
20.如图,已知∠2=∠4,∠3=∠B.
(1)试判断∠AED与∠C的关系,并说明理由;
(2)若∠1=130°,∠5=65°,求∠DGB的度数.
21.如图,已知∠C+∠CFD=180°,∠C=∠EDF,AF⊥DE于点G,DH⊥BC于点H,AG=DH=3.
(1)求证:DE∥BC;
(2)求点A到BC的距离.
22.如图,CD∥AB,∠DCB=70°,∠CBF=20°,∠EFB=130°.
(1)直线EF与AB有怎样的位置关系?说明理由;
(2)若∠CEF=68°,则∠ACB的度数是多少?
23.如图1,已知BE平分∠ABD,DE平分∠BDC,且∠EBD+∠EDB=90°.
(1)求证:AB∥CD;
(2)如图2.射线BF、DF交于点F,且∠BFD=30°,当∠ABE=3∠ABF时,试探决∠CDF与∠CDE的比值,并说明理由;
(3)若点H是直线CD上一动点(不与点D重合),BI平分∠HBD.请直接写出∠EBI与∠BHD的数量关系.
24.如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠AEF与∠EFC的角平分线交于点P,EP延长线与CD交于点G,点H是MN上一点,且PF∥GH,试判断直GH与EG的位置关系,并说明理由.
参考答案
1.解:如图,
∵∠1=∠2,∠2=∠5,
∴∠1=∠5,
∴l1∥l2,
∴∠3=∠6,
∵∠3=56°,
∴∠6=56°,
∵∠4+∠6=180°,
∴∠4=180°﹣56°=124°,
故选:C.
2.解:∵∠1=∠2=36°,
∴AC∥DE,
∴∠ACB=∠3,
∵CD平分∠ACB,
∴∠ACB=2∠1=72°,
∴∠3=72°.
故选:C.
3.解:①不相交的两条直线是平行线;此说法错误,应强调在同一平面内;
②在同一平面内,两条直线的位置关系有两种,正确,有相交或平行两种关系;
③若直线AB与CD没有交点,则AB∥CD;此说法错误,应强调在同一平面内;
④若a∥b,b∥c,则a与c不相交;根据平行公理的推论:如果两条直线都和第三条直线平行,那么两条直线也互相平行,上面说法正确.
故说法正确的有2个.
故选:B.
4.解:①∵AD∥BC,
∴∠2=∠3,
∵∠1=∠3,
∴∠1=∠2,
∴BD是∠ABC的平分线,故①正确;
②若AD∥BC,则∠2=∠3,并不能推出∠1与∠2和∠3的关系,故②错误;
③由“同旁内角互补,两直线平行”可知:若∠3+∠4+∠C=180°,则AD∥BC,故③正确;
④由“内错角相等,两直线平行”可知,若∠2=∠3,则AD∥BC,故④正确;
综上,正确的个数是3,
故选:C.
5.解:∠BAC=∠DCA,根据“内错角相等,两直线平行”可判定AB∥CD,不能判定AD∥BC,故A不符合题意;
∠ABC=∠ADC,不能判定AD∥BC,故B不符合题意;
∠DAC=∠BCA,根据“内错角相等,两直线平行”可判定AD∥BC,故C符合题意;
∠ABC+∠BCD=180°,根据“同旁内角互补,两直线平行”可判定AB∥CD,不能判定AD∥BC,故A不符合题意;
故选:C.
6.解:①∵AB⊥BC,DC⊥BC,
∴AB∥CD,
∴∠BAD+∠ADC=180°,
故①正确;
②∵AB∥CD,
∴∠AFD+∠BAF=180°,
∵∠BAF=∠EDF,
∴∠AFD+∠EDF=180°,
∴AF∥DE,
故②正确;
③∵AF∥ED,
∴∠DAF=∠ADE,∠F=∠CDE,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DAF=∠F,
故③正确;
故选:A.
7.解:∵四边形ABCD中∠ABC+∠C=180°,
∴AB∥DC,
∴∠2=∠4.
故选:D.
8.解:∵∠C=∠CAF,
∴AB∥CD,
∵∠BAC+∠C=180°,
∴AB∥CD,
∵∠GDE+∠B=180°,∠GDE+∠EDB=180°,
∴∠EDB=∠B,
∴AB∥CD,
所以能判断AB∥CD的是①∠C=∠CAF,③∠BAC+∠C=180°,④∠GDE+∠B=180°,
故选:C.
9.解:∵∠BAD+∠ADE=180°,
∴AB∥DE.
∴∠CDA=∠BAD=55°.
∵∠1+∠2+∠CDA=180°,
∴∠2=180°﹣∠1﹣∠CDA=180°﹣70°﹣55°=55°.
故选:C.
10.解:∵∠1=∠BEF=72°,
∴AB∥CD.
∴∠EGF=∠GEB.
∵EG平分∠BEF,
∴∠GEB=∠BEF=36°.
∴∠EGF=∠GEB=36°.
故选:B.
11.解:∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°﹣90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°﹣90°=45°,
∴∠F=180°﹣(∠FAD+∠FDA)=180﹣45°=135°,故④正确.
综上所述正确的有:①③④,共3个.
故选:C.
12.解:∵∠1=80°,
∴∠5=100°.
∵∠2=100°,∠3=76°,
∴∠2=∠5,
∴a∥b.
∴∠4=∠3=76°.
故答案为:76.
13.解:①∵AB∥DC,∴∠ABC+∠C=180°,此结论正确;
②∵∠1=∠2,∴AD∥BC,此结论正确;
③∵AD∥BC,∴∠1=∠2,而∠3≠∠4,此结论错误,
④∵∠A+∠ADC=180°,∴AB∥DC,此结论正确.
故答案为①②④.
14.解:与∠FCD相等的角有4个,它们分别是∠1、∠F、∠A、∠ABG.
故答案是:4;∠1、∠F、∠A、∠ABG.
15.解:如图,
∵∠1=∠2,
∴AD∥BC,
∴∠3+∠4=180°,
而∠3=100°,
∴∠4=180°﹣100°=80°.
故答案为80°.
16.解:∵EF⊥AC,DB⊥AC,
∴∠EFC=∠DMC=90°,
∴BD∥FE,
∴∠2=∠BDC,
∵∠1=∠2,
∴∠1=∠BDC,
∴MN∥CD,
∵∠3=∠C,
∴AB∥CD,
∴MN∥AB,
∴∠BAN+∠ANM=180°,
∵∠ANM=70°,
∴∠BAN=110°,
故答案为:110°.
17.解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF=BEF=31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
18.解:(1)AC∥DG,理由如下:
∵∠ABF=∠1,∠1=∠2,
∴∠ABF=∠2,
∴AC∥DG;
(2)由(1)知AC∥DG,
∴∠ABF=∠BFG,
∵∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,
∴,∠CFB=∠BFG,
∴∠EBF=∠CFB,
∴BE∥CF.
(3)∵AC∥DG,∠C=35°,
∴∠C=∠CFG=35°,
∵BE∥CF,
∴∠CFG=∠BEG=35°,
∴∠BED=180°﹣∠BEG=145°.
19.证明:∵∠DFE=∠2,∠D=180°﹣∠4﹣∠DFE,∠A=180°﹣∠3﹣∠1,
∴∠D=180°﹣∠4﹣∠2,
∴∠A=∠D,
∵AE∥BD,
∴∠A=∠DBC,
∴∠D=∠DBC,
∴ED∥AC.
20.解:(1)∠AED=∠C,理由如下:
∵∠2=∠4,
∴BD∥EF,
∴∠BDE+∠3=180°,
∵∠3=∠B,
∴∠BDE+∠B=180°,
∴DE∥BC,
∴∠AED=∠C;
(2)∵∠1+∠4=180°,∠1=130°,
∴∠4=50°,
∵∠2=∠4,
∴∠2=50°,
∵DE∥BC,
∴∠5=∠B,
∵∠5=65°,
∴∠B=65°,
在△BDG,∠B+∠2+∠DGB=180°,∠B=65°,∠2=50°,
∴∠DGB=65°.
21.(1)证明:∵∠C+∠CFD=180°,∠C=∠EDF,
∴∠EDF+∠CFD=180°,
∴DE∥BC;
(2)解:由(1)知DE∥BC,
∵AF⊥DE,
∴AF⊥BC,
∴AF的长是点A到BC的距离,
∵DH⊥BC,
∴DH∥AF,
∵DE∥BC,
∴四边形DHFG是平行四边形,
∴DH=GF,
∵AG=DH=3,
∴AF=AG+GF=3+3=6.
22.解:(1)EF和AB的位置关系为平行关系.理由如下:
∵CD∥AB,∠DCB=70°,
∴∠DCB=∠ABC=70°,
∵∠CBF=20°,
∴∠ABF=∠ABC﹣∠CBF=50°,
∵∠EFB=130°,
∴∠ABF+∠EFB=50°+130°=180°,
∴EF∥AB;
(2)∵EF∥AB,CD∥AB,
∴EF∥CD,
∵∠CEF=68°,
∴∠ECD=112°,
∵∠DCB=70°,
∴∠ACB=∠ECD﹣∠DCB,
∴∠ACB=42°.
23.证明:(1)∵BE平分∠ABD,DE平分∠BDC,
∴∠ABD=2∠EBD,∠CDB=2∠EDB,
又∵∠EBD+∠EDB=90°,
∴∠ABD+∠CBD=2×90°=180°,
∴AB∥CD;
(2)=,理由如下:
作EP∥AB,FQ∥AB,如图2,
又∵AB∥CD,
∴AB∥CD∥EP,AB∥CD∥FQ,
∴∠ABE=∠BEP,∠DEP=∠CDE,
∴∠BED=∠BEP+∠DEP=∠ABE+∠CDE=90°,
同理,∠BFD=∠ABF+∠CDF,
∵∠ABE=3∠ABF,∠BFD=30°,
∴∠BFD=∠ABE+∠CDF=30°=∠BED,
∴=;
(3)∵BE平分∠ABD,
∴∠ABD=2∠EBD,
∵BI平分∠HBD,
∴∠HBD=2∠IBD,
如图1,点H在点D的左边时,∠ABH=∠ABD﹣∠HBD,∠EBI=∠EBD﹣∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=∠ABH,
∴∠BHD=2∠EBI,
如图2,点H在点D的右边时,∠ABH=∠ABD+∠HBD,
∠EBI=∠EBD+∠IBD,
∴∠ABH=2∠EBI,
∵AB∥CD,
∴∠BHD=180°﹣∠ABH,
∴∠BHD=180°﹣2∠EBI,
综上所述,∠BHD=2∠EBI或∠BHD=180°﹣2∠EBI.
24.解:(1)AB∥CD,理由如下:
∵∠1与∠2互补,
∴∠1+∠2=180°,
又∵∠2+∠CFE=180°,
∴∠1=∠CFE,
∴AB∥CD;
(2)GH⊥EG,理由如下:
由(1)知,AB∥CD,
∴∠AEF+∠EFC=180°.
又∵∠AEF与∠EFC的角平分线交于点P,
∴∠FEP+∠EFP=(∠BEF+∠EFD)=90°,
∴∠EPF=90°,即EG⊥PF,
∵PF∥GH,
∴GH⊥EG.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
