【备考2022】泰安市近十年中考数学考点10 圆的基本概念、性质的运用(含答案)
文档属性
| 名称 | 【备考2022】泰安市近十年中考数学考点10 圆的基本概念、性质的运用(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 261.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 11:24:25 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
十、圆的基本概念、性质的运用
[基础知识]
圆的有关概念及性质,圆的对称性(轴对称、中心对称、旋转对称)
确定圆的条件。
垂径定理:RT△ :弦的一半2+弦心距2=半径2;垂径及其推论。
圆心角与圆周角
弦、弧、圆心角的关系
[中考真题]
(2021)6.(4分)如图,在△ABC中,AB=6,以点A为圆心,3为半径的圆与边BC相切于点D,与AC,AB分别交于点E和点G,点F是优弧GE上一点,∠CDE=18°,则∠GFE的度数是( )
A.50° B.48° C.45° D.36°
(2020)6.如图,PA是⊙O的切线,点A为切点,OP交⊙O于点B,∠P=10°,点C在⊙O上,OC∥AB.则∠BAC等于( )
A.20° B.25° C.30° D.50°
(2019)9.(4分)如图,△ABC是⊙O的内接三角形,∠A=119°,过点C的圆的切线交BO于点P,则∠P的度数为( )
A.32° B.31°
C.29° D.61°
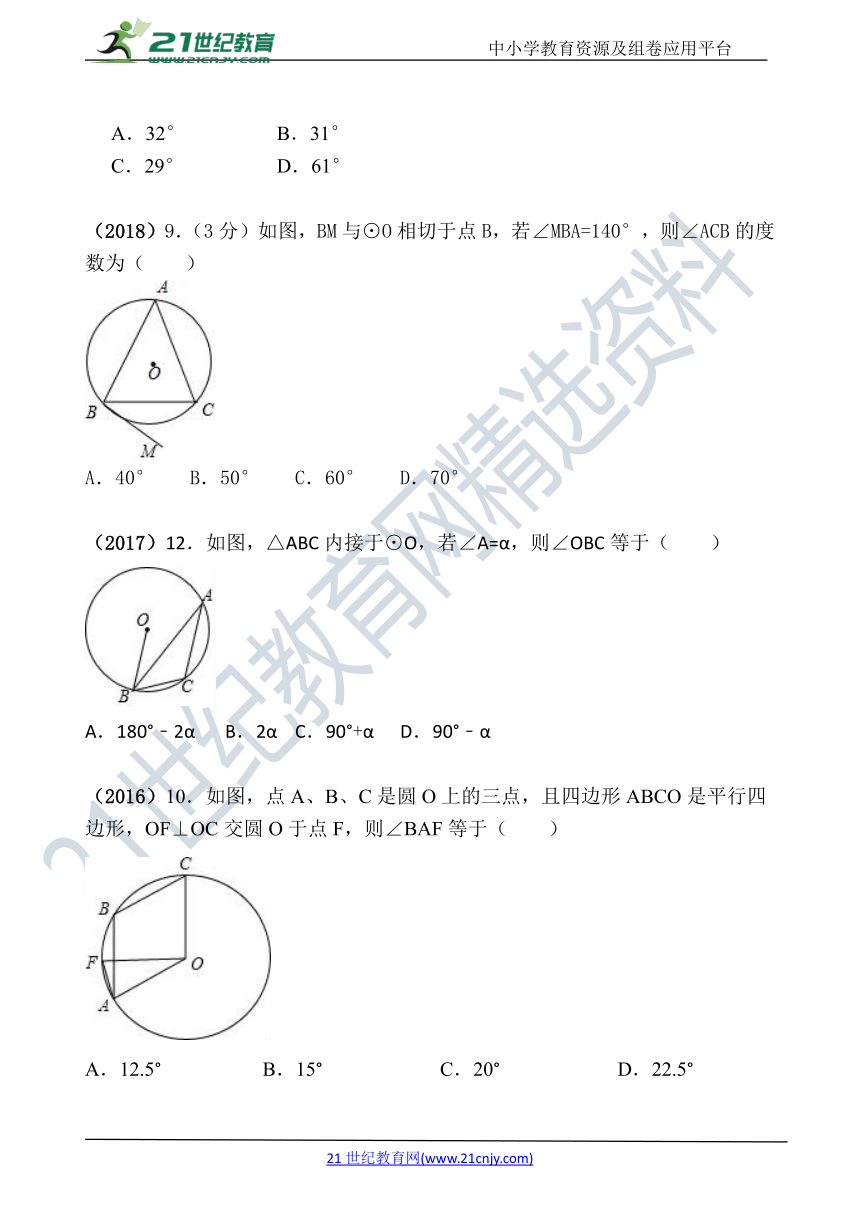
(2018)9.(3分)如图,BM与⊙O相切于点B,若∠MBA=140°,则∠ACB的度数为( )
A.40° B.50° C.60° D.70°
(2017)12.如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于( )
A.180°﹣2α B.2α C.90°+α D.90°﹣α
(2016)10.如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15° C.20° D.22.5°
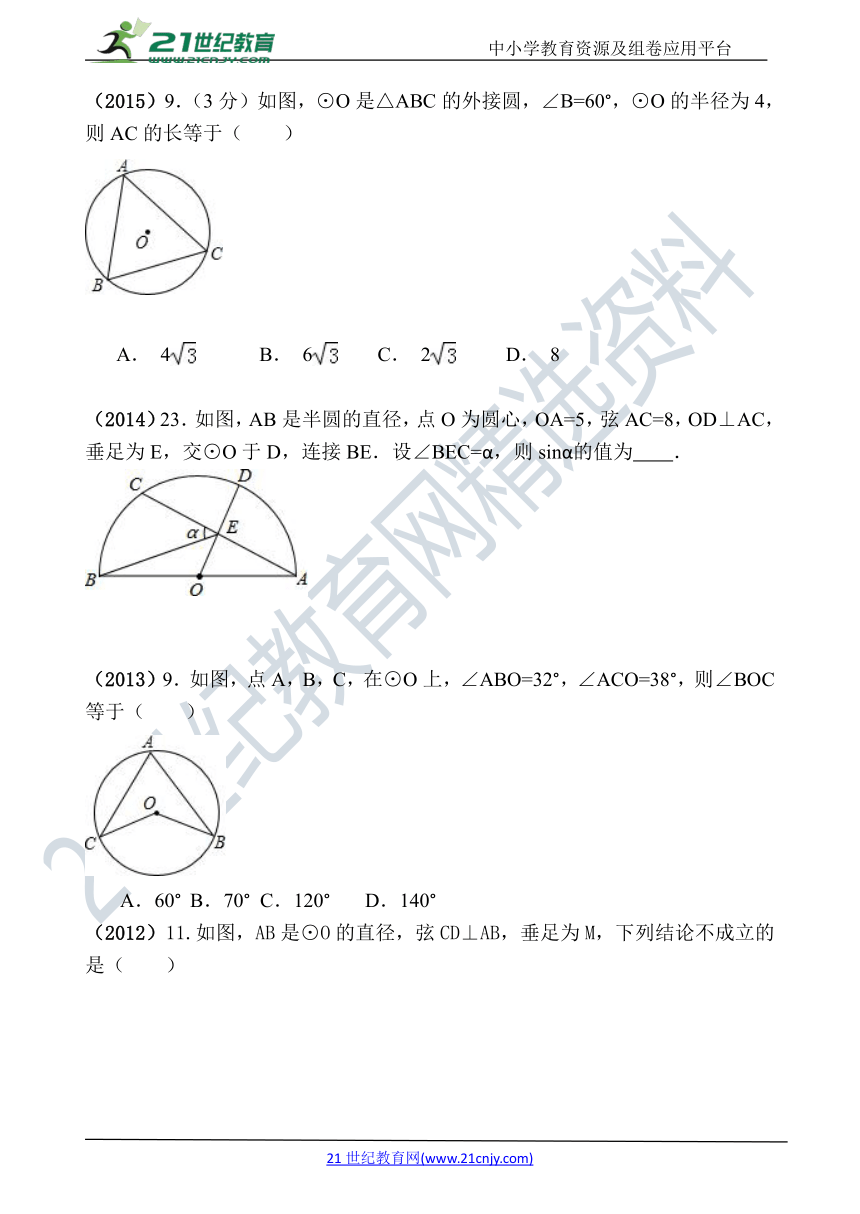
(2015)9.(3分)如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
( http: / / www.21cnjy.com / )
A. 4 B. 6 C. 2 D. 8
(2014)23.如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则sinα的值为 .
(2013)9.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )
A.60° B.70° C.120° D.140°
(2012)11.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B.CB=DB C.∠ACD=∠ADC D.OM=MD
[答案解析]
(2021)6.(4分)如图,在△ABC中,AB=6,以点A为圆心,3为半径的圆与边BC相切于点D,与AC,AB分别交于点E和点G,点F是优弧GE上一点,∠CDE=18°,则∠GFE的度数是( )
A.50° B.48° C.45° D.36°
【分析】 应用切线性质、圆周角定理等的求解。
【解答】:连接AD,
∵BC与⊙A相切于点D,
∴AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AB=6,AG=AD=3,
∴AD=AB,
∴∠B=30°,
∴∠GAD=60°,
∵∠CDE=18°,
∴∠ADE=90°﹣18°=72°,
∵AD=AE,
∴∠AED=∠ADE=72°,
∴∠DAE=180°﹣∠ADE﹣∠AED=180°﹣72°﹣72°=36°,
∴∠BAC=∠BAD+∠CAD=60°+36°=96°,
∴∠GFE=GAE=96°=48°,
故选:B.
(2020)6.如图,PA是⊙O的切线,点A为切点,OP交⊙O于点B,∠P=10°,点C在⊙O上,OC∥AB.则∠BAC等于( )
A.20° B.25° C.30° D.50°
【分析】 连接OA,根据切线的性质得到∠PAO=90°,求出∠AOP,根据等腰三角形的性质、平行线的性质求出∠BOC,根据圆周角定理解答即可.
【解答】:连接OA,
∵PA是⊙O的切线,
∴OA⊥AP,
∴∠PAO=90°,
∴∠AOP=90°﹣∠P=80°,
∵OA=OB,
∴∠OAB=∠OBA=50°,
∵OC∥AB,
∴∠BOC=∠OBA=50°,
由圆周角定理得,∠BAC=∠BOC=25°,
故选:B.
(2019)9.(4分)如图,△ABC是⊙O的内接三角形,∠A=119°,过点C的圆的切线交BO于点P,则∠P的度数为( )
A.32° B.31°
C.29° D.61°
【分析】连接OC、CD,由切线的性质得出∠OCP=90°,由圆内接四边形的性质得出∠ODC=180°﹣∠A=61°,由等腰三角形的性质得出∠OCD=∠ODC=61°,求出∠DOC=58°,由直角三角形的性质即可得出结果.
【解答】解:如图所示:连接OC、CD,
∵PC是⊙O的切线,
∴PC⊥OC,
∴∠OCP=90°,
∵∠A=119°,
∴∠ODC=180°﹣∠A=61°,
∵OC=OD,
∴∠OCD=∠ODC=61°,
∴∠DOC=180°﹣2×61°=58°,
∴∠P=90°﹣∠DOC=32°;
故选:A.
【总结】本题考查了切线的性质、等腰三角形的性质、直角三角形的性质、三角形内角和定理;熟练掌握切线的性质是解题的关键.
(2018)9.(3分)如图,BM与⊙O相切于点B,若∠MBA=140°,则∠ACB的度数为( )
A.40° B.50° C.60° D.70°
【分析】 连接OA、OB,由切线的性质知∠OBM=90°,从而得∠ABO=∠BAO=50°,由内角和定理知∠AOB=80°,根据圆周角定理可得答案.
【解答】解:如图,连接OA、OB,
∵BM是⊙O的切线,
∴∠OBM=90°,
∵∠MBA=140°,
∴∠ABO=50°,
∵OA=OB,
∴∠ABO=∠BAO=50°,
∴∠AOB=80°,
∴∠ACB=∠AOB=40°,
故选:A.
【总结】本题主要考查切线的性质,解题的关键是掌握切线的性质:①圆的切线垂直于经过切点的半径.②经过圆心且垂直于切线的直线必经过切点.③经过切点且垂直于切线的直线必经过圆心.
(2017)12.如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于( )
A.180°﹣2α B.2α C.90°+α D.90°﹣α
【分析】首先连接OC,由圆周角定理,可求得∠BOC的度数,又由等腰三角形的性质,即可求得∠OBC的度数.
【解答】解:∵连接OC,
∵△ABC内接于⊙O,∠A=α,
∴∠BOC=2∠A=2α,
∵OB=OC,
∴∠OBC=∠OCB==90°﹣α.
故选D.
(2016)10.如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15° C.20° D.22.5°
【分析】根据平行四边形的性质和圆的半径相等得到△AOB为等边三角形,根据等腰三角形的三线合一得到∠BOF=∠AOF=30°,根据圆周角定理计算即可.
【解答】解:连接OB,
∵四边形ABCO是平行四边形,
∴OC=AB,又OA=OB=OC,
∴OA=OB=AB,
∴△AOB为等边三角形,
∵OF⊥OC,OC∥AB,
∴OF⊥AB,
∴∠BOF=∠AOF=30°,
由圆周角定理得∠BAF=∠BOF=15°,
故选:B.
【总结】本题考查的是圆周角定理、平行四边形的性质定理、等边三角形的性质的综合运用,掌握同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半、等腰三角形的三线合一是解题的关键.
(2015)9.(3分)如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
( http: / / www.21cnjy.com / )
A. 4 B. 6 C. 2 D. 8
【分析】
首先连接OA,OC,过点O ( http: / / www.21cnjy.com )作OD⊥AC于点D,由圆周角定理可求得∠AOC的度数,进而可在构造的直角三角形中,根据勾股定理求得弦AC的一半,由此得解.
【解答】:解:连接OA,OC,过点O作OD⊥AC于点D,
∵∠AOC=2∠B,且∠AOD=∠COD=∠AOC,
∴∠COD=∠B=60°;
在Rt△COD中,OC=4,∠COD=60°,
∴CD=OC=2,
∴AC=2CD=4.
故选A.
( http: / / www.21cnjy.com )
【总结】 此题主要考查了三角形的外接圆以及勾股定理的应用,还涉及到圆周角定理、垂径定理以及直角三角形的性质等知识.
(2014)23.如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则sinα的值为 .
【分析】连结BC,根据圆周角定理由AB是半圆的直径得∠ACB=90°,在Rt△ABC中,根据勾股定理计算出BC=6,再根据垂径定理由OD⊥AC得到AE=CE=AC=4,然后在Rt△BCE中,根据勾股定理计算出BE=2,则可根据正弦的定义求解.
【解答】:连结BC,如图,∵AB是半圆的直径,∴∠ACB=90°,
在Rt△ABC中,AC=8,AB=10,∴BC==6,
∵OD⊥AC,∴AE=CE=AC=4,
在Rt△BCE中,BE==2,
∴sinα===.故答案为.
【总结】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和圆周角定理.
(2013)9.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )
A.60° B.70° C.120° D.140°
【分析】 过A、O作⊙O的直径AD,分别在等腰△OAB、等腰△OAC中,根据三角形外角的性质求出θ=2α+2β.
【解答】:过A作⊙O的直径,交⊙O于D;
△OAB中,OA=OB,
则∠BOD=∠OBA+∠OAB=2×32°=64°,
同理可得:∠COD=∠OCA+∠OAC=2×38°=76°,
故∠BOC=∠BOD+∠COD=140°.
故选D
【总结】本题考查了圆周角定理,涉及了等腰三角形的性质及三角形的外角性质,解答本题的关键是求出∠COD及∠BOD的度数.
(2012)11.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B.CB=DB C.∠ACD=∠ADC D.OM=MD
【分析】垂径定理。
【解答】:∵AB是⊙O的直径,弦CD⊥AB,垂足为M,
∴M为CD的中点,即CM=DM,选项A成立;
B为的中点,即,选项B成立;
在△ACM和△ADM中,
∵AM=AM,∠AMC=∠AMD=90°,CM=DM,
∴△ACM≌△ADM(SAS),
∴∠ACD=∠ADC,选项C成立;
而OM与MD不一定相等,选项D不成立.
故选D
[解题攻略]
熟练掌握切线的性质,圆心角、圆周角定理,垂径定理,正确的作出辅助线是解题的关键.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
十、圆的基本概念、性质的运用
[基础知识]
圆的有关概念及性质,圆的对称性(轴对称、中心对称、旋转对称)
确定圆的条件。
垂径定理:RT△ :弦的一半2+弦心距2=半径2;垂径及其推论。
圆心角与圆周角
弦、弧、圆心角的关系
[中考真题]
(2021)6.(4分)如图,在△ABC中,AB=6,以点A为圆心,3为半径的圆与边BC相切于点D,与AC,AB分别交于点E和点G,点F是优弧GE上一点,∠CDE=18°,则∠GFE的度数是( )
A.50° B.48° C.45° D.36°
(2020)6.如图,PA是⊙O的切线,点A为切点,OP交⊙O于点B,∠P=10°,点C在⊙O上,OC∥AB.则∠BAC等于( )
A.20° B.25° C.30° D.50°
(2019)9.(4分)如图,△ABC是⊙O的内接三角形,∠A=119°,过点C的圆的切线交BO于点P,则∠P的度数为( )
A.32° B.31°
C.29° D.61°
(2018)9.(3分)如图,BM与⊙O相切于点B,若∠MBA=140°,则∠ACB的度数为( )
A.40° B.50° C.60° D.70°
(2017)12.如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于( )
A.180°﹣2α B.2α C.90°+α D.90°﹣α
(2016)10.如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15° C.20° D.22.5°
(2015)9.(3分)如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
( http: / / www.21cnjy.com / )
A. 4 B. 6 C. 2 D. 8
(2014)23.如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则sinα的值为 .
(2013)9.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )
A.60° B.70° C.120° D.140°
(2012)11.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B.CB=DB C.∠ACD=∠ADC D.OM=MD
[答案解析]
(2021)6.(4分)如图,在△ABC中,AB=6,以点A为圆心,3为半径的圆与边BC相切于点D,与AC,AB分别交于点E和点G,点F是优弧GE上一点,∠CDE=18°,则∠GFE的度数是( )
A.50° B.48° C.45° D.36°
【分析】 应用切线性质、圆周角定理等的求解。
【解答】:连接AD,
∵BC与⊙A相切于点D,
∴AD⊥BC,
∴∠ADB=∠ADC=90°,
∵AB=6,AG=AD=3,
∴AD=AB,
∴∠B=30°,
∴∠GAD=60°,
∵∠CDE=18°,
∴∠ADE=90°﹣18°=72°,
∵AD=AE,
∴∠AED=∠ADE=72°,
∴∠DAE=180°﹣∠ADE﹣∠AED=180°﹣72°﹣72°=36°,
∴∠BAC=∠BAD+∠CAD=60°+36°=96°,
∴∠GFE=GAE=96°=48°,
故选:B.
(2020)6.如图,PA是⊙O的切线,点A为切点,OP交⊙O于点B,∠P=10°,点C在⊙O上,OC∥AB.则∠BAC等于( )
A.20° B.25° C.30° D.50°
【分析】 连接OA,根据切线的性质得到∠PAO=90°,求出∠AOP,根据等腰三角形的性质、平行线的性质求出∠BOC,根据圆周角定理解答即可.
【解答】:连接OA,
∵PA是⊙O的切线,
∴OA⊥AP,
∴∠PAO=90°,
∴∠AOP=90°﹣∠P=80°,
∵OA=OB,
∴∠OAB=∠OBA=50°,
∵OC∥AB,
∴∠BOC=∠OBA=50°,
由圆周角定理得,∠BAC=∠BOC=25°,
故选:B.
(2019)9.(4分)如图,△ABC是⊙O的内接三角形,∠A=119°,过点C的圆的切线交BO于点P,则∠P的度数为( )
A.32° B.31°
C.29° D.61°
【分析】连接OC、CD,由切线的性质得出∠OCP=90°,由圆内接四边形的性质得出∠ODC=180°﹣∠A=61°,由等腰三角形的性质得出∠OCD=∠ODC=61°,求出∠DOC=58°,由直角三角形的性质即可得出结果.
【解答】解:如图所示:连接OC、CD,
∵PC是⊙O的切线,
∴PC⊥OC,
∴∠OCP=90°,
∵∠A=119°,
∴∠ODC=180°﹣∠A=61°,
∵OC=OD,
∴∠OCD=∠ODC=61°,
∴∠DOC=180°﹣2×61°=58°,
∴∠P=90°﹣∠DOC=32°;
故选:A.
【总结】本题考查了切线的性质、等腰三角形的性质、直角三角形的性质、三角形内角和定理;熟练掌握切线的性质是解题的关键.
(2018)9.(3分)如图,BM与⊙O相切于点B,若∠MBA=140°,则∠ACB的度数为( )
A.40° B.50° C.60° D.70°
【分析】 连接OA、OB,由切线的性质知∠OBM=90°,从而得∠ABO=∠BAO=50°,由内角和定理知∠AOB=80°,根据圆周角定理可得答案.
【解答】解:如图,连接OA、OB,
∵BM是⊙O的切线,
∴∠OBM=90°,
∵∠MBA=140°,
∴∠ABO=50°,
∵OA=OB,
∴∠ABO=∠BAO=50°,
∴∠AOB=80°,
∴∠ACB=∠AOB=40°,
故选:A.
【总结】本题主要考查切线的性质,解题的关键是掌握切线的性质:①圆的切线垂直于经过切点的半径.②经过圆心且垂直于切线的直线必经过切点.③经过切点且垂直于切线的直线必经过圆心.
(2017)12.如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于( )
A.180°﹣2α B.2α C.90°+α D.90°﹣α
【分析】首先连接OC,由圆周角定理,可求得∠BOC的度数,又由等腰三角形的性质,即可求得∠OBC的度数.
【解答】解:∵连接OC,
∵△ABC内接于⊙O,∠A=α,
∴∠BOC=2∠A=2α,
∵OB=OC,
∴∠OBC=∠OCB==90°﹣α.
故选D.
(2016)10.如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
A.12.5° B.15° C.20° D.22.5°
【分析】根据平行四边形的性质和圆的半径相等得到△AOB为等边三角形,根据等腰三角形的三线合一得到∠BOF=∠AOF=30°,根据圆周角定理计算即可.
【解答】解:连接OB,
∵四边形ABCO是平行四边形,
∴OC=AB,又OA=OB=OC,
∴OA=OB=AB,
∴△AOB为等边三角形,
∵OF⊥OC,OC∥AB,
∴OF⊥AB,
∴∠BOF=∠AOF=30°,
由圆周角定理得∠BAF=∠BOF=15°,
故选:B.
【总结】本题考查的是圆周角定理、平行四边形的性质定理、等边三角形的性质的综合运用,掌握同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半、等腰三角形的三线合一是解题的关键.
(2015)9.(3分)如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
( http: / / www.21cnjy.com / )
A. 4 B. 6 C. 2 D. 8
【分析】
首先连接OA,OC,过点O ( http: / / www.21cnjy.com )作OD⊥AC于点D,由圆周角定理可求得∠AOC的度数,进而可在构造的直角三角形中,根据勾股定理求得弦AC的一半,由此得解.
【解答】:解:连接OA,OC,过点O作OD⊥AC于点D,
∵∠AOC=2∠B,且∠AOD=∠COD=∠AOC,
∴∠COD=∠B=60°;
在Rt△COD中,OC=4,∠COD=60°,
∴CD=OC=2,
∴AC=2CD=4.
故选A.
( http: / / www.21cnjy.com )
【总结】 此题主要考查了三角形的外接圆以及勾股定理的应用,还涉及到圆周角定理、垂径定理以及直角三角形的性质等知识.
(2014)23.如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则sinα的值为 .
【分析】连结BC,根据圆周角定理由AB是半圆的直径得∠ACB=90°,在Rt△ABC中,根据勾股定理计算出BC=6,再根据垂径定理由OD⊥AC得到AE=CE=AC=4,然后在Rt△BCE中,根据勾股定理计算出BE=2,则可根据正弦的定义求解.
【解答】:连结BC,如图,∵AB是半圆的直径,∴∠ACB=90°,
在Rt△ABC中,AC=8,AB=10,∴BC==6,
∵OD⊥AC,∴AE=CE=AC=4,
在Rt△BCE中,BE==2,
∴sinα===.故答案为.
【总结】本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和圆周角定理.
(2013)9.如图,点A,B,C,在⊙O上,∠ABO=32°,∠ACO=38°,则∠BOC等于( )
A.60° B.70° C.120° D.140°
【分析】 过A、O作⊙O的直径AD,分别在等腰△OAB、等腰△OAC中,根据三角形外角的性质求出θ=2α+2β.
【解答】:过A作⊙O的直径,交⊙O于D;
△OAB中,OA=OB,
则∠BOD=∠OBA+∠OAB=2×32°=64°,
同理可得:∠COD=∠OCA+∠OAC=2×38°=76°,
故∠BOC=∠BOD+∠COD=140°.
故选D
【总结】本题考查了圆周角定理,涉及了等腰三角形的性质及三角形的外角性质,解答本题的关键是求出∠COD及∠BOD的度数.
(2012)11.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B.CB=DB C.∠ACD=∠ADC D.OM=MD
【分析】垂径定理。
【解答】:∵AB是⊙O的直径,弦CD⊥AB,垂足为M,
∴M为CD的中点,即CM=DM,选项A成立;
B为的中点,即,选项B成立;
在△ACM和△ADM中,
∵AM=AM,∠AMC=∠AMD=90°,CM=DM,
∴△ACM≌△ADM(SAS),
∴∠ACD=∠ADC,选项C成立;
而OM与MD不一定相等,选项D不成立.
故选D
[解题攻略]
熟练掌握切线的性质,圆心角、圆周角定理,垂径定理,正确的作出辅助线是解题的关键.
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
