2021-2022学年高一下学期数学人教A版(2019)必修第二册7.1数系的扩充和复数的概念课件(15张ppt)
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版(2019)必修第二册7.1数系的扩充和复数的概念课件(15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 386.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 20:41:06 | ||
图片预览




文档简介
(共15张PPT)
7.1.1数系的扩充和复数的概念
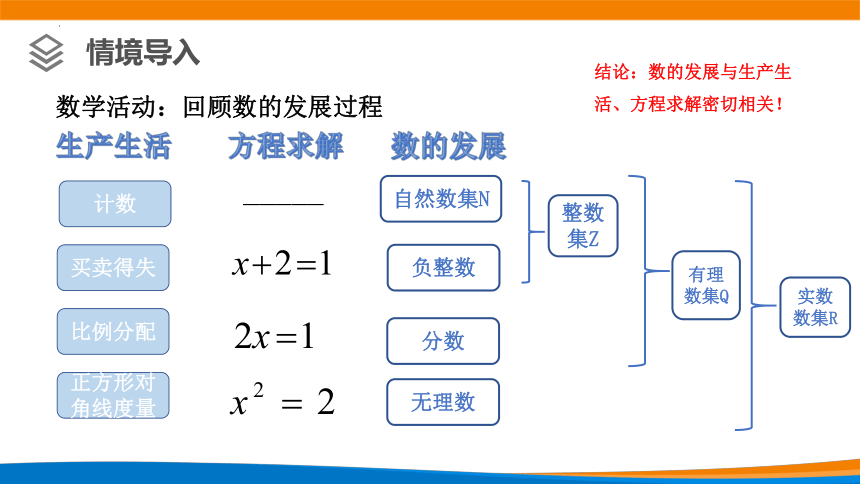
数学活动:回顾数的发展过程
生产生活
方程求解
数的发展
计数
买卖得失
比例分配
正方形对角线度量
自然数集N
负整数
分数
无理数
整数集Z
有理数集Q
实数数集R
—————
结论:数的发展与生产生活、方程求解密切相关!
情境导入
探究交流
追问1:我们知道,像 这些方程在实数集中是无解的,那能否类比从自然数集到实数集的扩充过程,通过引进新的数而使实数集得到扩充,从而使方程有解?
为了让x2=-1有解,引入一个“新数i”,使得 ,如此一来,
x=i 就是方程x2+1=0 的解.
在1777年,欧拉在《微分公式》一文中首创了用“imaginary”(想象的、假想的)的首字母i作为虚数的单位,本意是这个数是虚幻的,规定了i2=-1.
问题1:能否求出方程x2+2x+2=0的解?
欧拉恒等式:
莱昂哈德·欧拉是18世纪最伟大的数学家之一,有一个以他名字命名的公式被誉为“上帝创造的公式”,那就是欧拉恒等式.
《物理世界》发起的一项调查表明,人们把欧拉恒等式与麦克斯韦方程组一起并称为“史上最伟大的公式”. 物理大师费曼也盛赞这个公式为“数学最非凡的公式”.
探究交流
探究交流
R
C
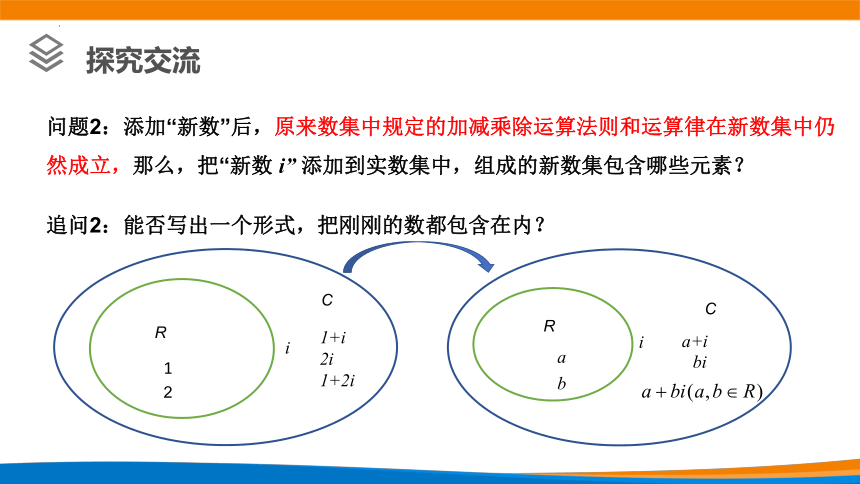
1
1+i
2i
1+2i
R
C
i
2
追问2:能否写出一个形式,把刚刚的数都包含在内?
问题2:添加“新数”后,原来数集中规定的加减乘除运算法则和运算律在新数集中仍然成立,那么,把“新数 i” 添加到实数集中,组成的新数集包含哪些元素?
a
b
i
a+i
bi
探究交流
R
C
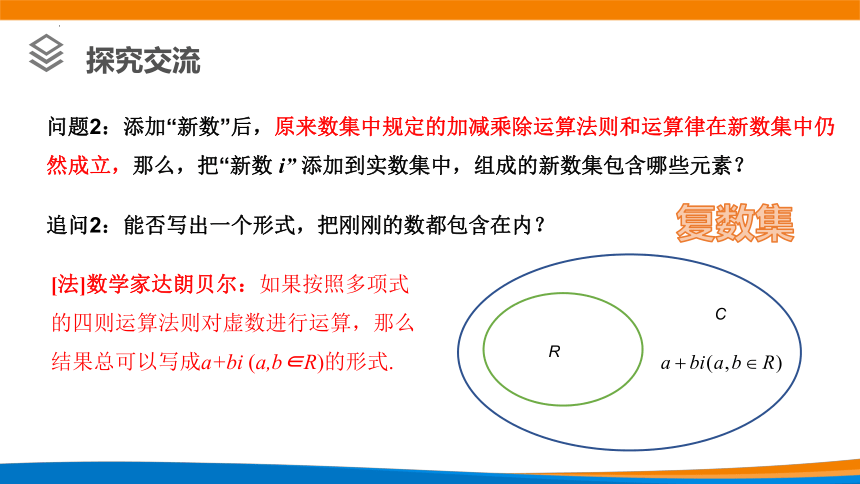
[法]数学家达朗贝尔:如果按照多项式的四则运算法则对虚数进行运算,那么结果总可以写成a+bi (a,b∈R)的形式.
复数集
追问2:能否写出一个形式,把刚刚的数都包含在内?
问题2:添加“新数”后,原来数集中规定的加减乘除运算法则和运算律在新数集中仍然成立,那么,把“新数 i” 添加到实数集中,组成的新数集包含哪些元素?
构建数学
(1)复数的定义
形如a+bi(a,b∈R)的数叫做复数,其中 i 叫做___________,规定i 2=______.
(2)复数集
全体复数所构成的集合C={a+bi|a,b∈R}叫做复数集.
(3)复数的表示方法
复数通常用字母z表示,即__________________,其中a叫做复数z的实部,b叫做复数z的虚部.
虚数单位
-1
z=a+bi(a,b∈R)
构建数学
问题3:复数z=a+bi(a,b∈R)是实数的充要条件是什么?
a=0,b=0
复数只能说相等或不相等,而只有当两个复数都是实数时才能比较大小,否则,不能比较大小.
z=a+bi=0的充要条件是什么?
b=0
(4)复数相等的充要条件
规定:在复数集C={a+bi|a,b∈R}中任取两个数a+bi,c+di(a,b,c,d∈R),a+bi与c+di相等当且仅当 a=c 且 b=d .
特殊到一般
实部和虚部分别相等
构建数学
问题4:进一步地,你能对复数z=a+bi(a,b∈R)进行分类吗?
(5)复数的分类
构建数学
问题5:我们已经将实数集扩充到了复数集,能否用韦恩图表示出数集N,Z,Q,R,C之间的关系?
N
Z
Q
R
C
新数集包含
原来的数集!
应用拓展
问题6:当实数m取什么值时,复数z=m+1+(m-1)i是下列数?
(1)实数;(2)虚数;(3)纯虚数.
解:(1)当m-1=0,即m=1时,复数z是实数.
(2)当m-1≠0,即m≠1时,复数z是虚数.
(3)当m+1=0,且m-1≠0,即m=-1时,复数z是纯虚数.
应用拓展
问题7:已知(x-y)+(y-2)i=(2x+3y)+(2y+1)i,求实数x,y的值.
解: 根据复数相等的充要条件,可得
解得
转化
课堂总结
问题8:本节课学了哪些知识和思想方法?
实数系的扩充
复数与复数集
复数相等的含义
实数、虚数、纯虚数之间的关系
逻辑推理、数学抽象
类比
特殊到一般、
转化
课外作业
教科书7.1.1的练习第1,2,3题.
再会!
7.1.1数系的扩充和复数的概念
数学活动:回顾数的发展过程
生产生活
方程求解
数的发展
计数
买卖得失
比例分配
正方形对角线度量
自然数集N
负整数
分数
无理数
整数集Z
有理数集Q
实数数集R
—————
结论:数的发展与生产生活、方程求解密切相关!
情境导入
探究交流
追问1:我们知道,像 这些方程在实数集中是无解的,那能否类比从自然数集到实数集的扩充过程,通过引进新的数而使实数集得到扩充,从而使方程有解?
为了让x2=-1有解,引入一个“新数i”,使得 ,如此一来,
x=i 就是方程x2+1=0 的解.
在1777年,欧拉在《微分公式》一文中首创了用“imaginary”(想象的、假想的)的首字母i作为虚数的单位,本意是这个数是虚幻的,规定了i2=-1.
问题1:能否求出方程x2+2x+2=0的解?
欧拉恒等式:
莱昂哈德·欧拉是18世纪最伟大的数学家之一,有一个以他名字命名的公式被誉为“上帝创造的公式”,那就是欧拉恒等式.
《物理世界》发起的一项调查表明,人们把欧拉恒等式与麦克斯韦方程组一起并称为“史上最伟大的公式”. 物理大师费曼也盛赞这个公式为“数学最非凡的公式”.
探究交流
探究交流
R
C
1
1+i
2i
1+2i
R
C
i
2
追问2:能否写出一个形式,把刚刚的数都包含在内?
问题2:添加“新数”后,原来数集中规定的加减乘除运算法则和运算律在新数集中仍然成立,那么,把“新数 i” 添加到实数集中,组成的新数集包含哪些元素?
a
b
i
a+i
bi
探究交流
R
C
[法]数学家达朗贝尔:如果按照多项式的四则运算法则对虚数进行运算,那么结果总可以写成a+bi (a,b∈R)的形式.
复数集
追问2:能否写出一个形式,把刚刚的数都包含在内?
问题2:添加“新数”后,原来数集中规定的加减乘除运算法则和运算律在新数集中仍然成立,那么,把“新数 i” 添加到实数集中,组成的新数集包含哪些元素?
构建数学
(1)复数的定义
形如a+bi(a,b∈R)的数叫做复数,其中 i 叫做___________,规定i 2=______.
(2)复数集
全体复数所构成的集合C={a+bi|a,b∈R}叫做复数集.
(3)复数的表示方法
复数通常用字母z表示,即__________________,其中a叫做复数z的实部,b叫做复数z的虚部.
虚数单位
-1
z=a+bi(a,b∈R)
构建数学
问题3:复数z=a+bi(a,b∈R)是实数的充要条件是什么?
a=0,b=0
复数只能说相等或不相等,而只有当两个复数都是实数时才能比较大小,否则,不能比较大小.
z=a+bi=0的充要条件是什么?
b=0
(4)复数相等的充要条件
规定:在复数集C={a+bi|a,b∈R}中任取两个数a+bi,c+di(a,b,c,d∈R),a+bi与c+di相等当且仅当 a=c 且 b=d .
特殊到一般
实部和虚部分别相等
构建数学
问题4:进一步地,你能对复数z=a+bi(a,b∈R)进行分类吗?
(5)复数的分类
构建数学
问题5:我们已经将实数集扩充到了复数集,能否用韦恩图表示出数集N,Z,Q,R,C之间的关系?
N
Z
Q
R
C
新数集包含
原来的数集!
应用拓展
问题6:当实数m取什么值时,复数z=m+1+(m-1)i是下列数?
(1)实数;(2)虚数;(3)纯虚数.
解:(1)当m-1=0,即m=1时,复数z是实数.
(2)当m-1≠0,即m≠1时,复数z是虚数.
(3)当m+1=0,且m-1≠0,即m=-1时,复数z是纯虚数.
应用拓展
问题7:已知(x-y)+(y-2)i=(2x+3y)+(2y+1)i,求实数x,y的值.
解: 根据复数相等的充要条件,可得
解得
转化
课堂总结
问题8:本节课学了哪些知识和思想方法?
实数系的扩充
复数与复数集
复数相等的含义
实数、虚数、纯虚数之间的关系
逻辑推理、数学抽象
类比
特殊到一般、
转化
课外作业
教科书7.1.1的练习第1,2,3题.
再会!
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
