浙江省宁波市海曙外国语学校2021-2022学年八年级下学期开学考试数学试卷(Word版无答案)
文档属性
| 名称 | 浙江省宁波市海曙外国语学校2021-2022学年八年级下学期开学考试数学试卷(Word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 149.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 17:20:27 | ||
图片预览

文档简介
2021-2022学年浙江省宁波市海曙外国语学校八年级(下)起始考数学试卷
一、选择题(每小题3分,共30分)
1.下列医护图案既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.下面计算正确的是( )
A.=±5 B.÷=4 C.(﹣)2=﹣5 D.3﹣=2
3.在下列方程中,是一元二次方程的是( )
A.x2+3x= B.2(x﹣1)+x=2 C.x2=2+3x D.x2﹣x3+4=0
4.若x=2能使下列二次根式有意义,则这个二次根式可以是( )
A. B. C. D.
5.已知平行四边形ABCD中,∠A+∠C=110°,则∠B的度数为( )
A.125° B.135° C.145° D.155°
6.将一个容积为600cm3的长方体包装盒剪开、铺平,纸样如图所示,根据题意,列出关于x的方程为( )
A.15(30﹣2x) x=600 B.30(30﹣2x) x=600
C.15(15﹣x) x=600 D.x(15﹣x) x=600
7.已知a是方程x2﹣2x﹣3=0的一个根,则代数式2a2﹣4a﹣1的值为( )
A.3 B.﹣4 C.3或﹣4 D.5
8.设a=6,b=,c=+,则a,b、c的大小关系是( )
A.b>c>a B.b>a>c C.c>a>b D.a>c>b
9.当b+c=5时,关于x的一元二次方程3x2+bx﹣c=0的根的情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
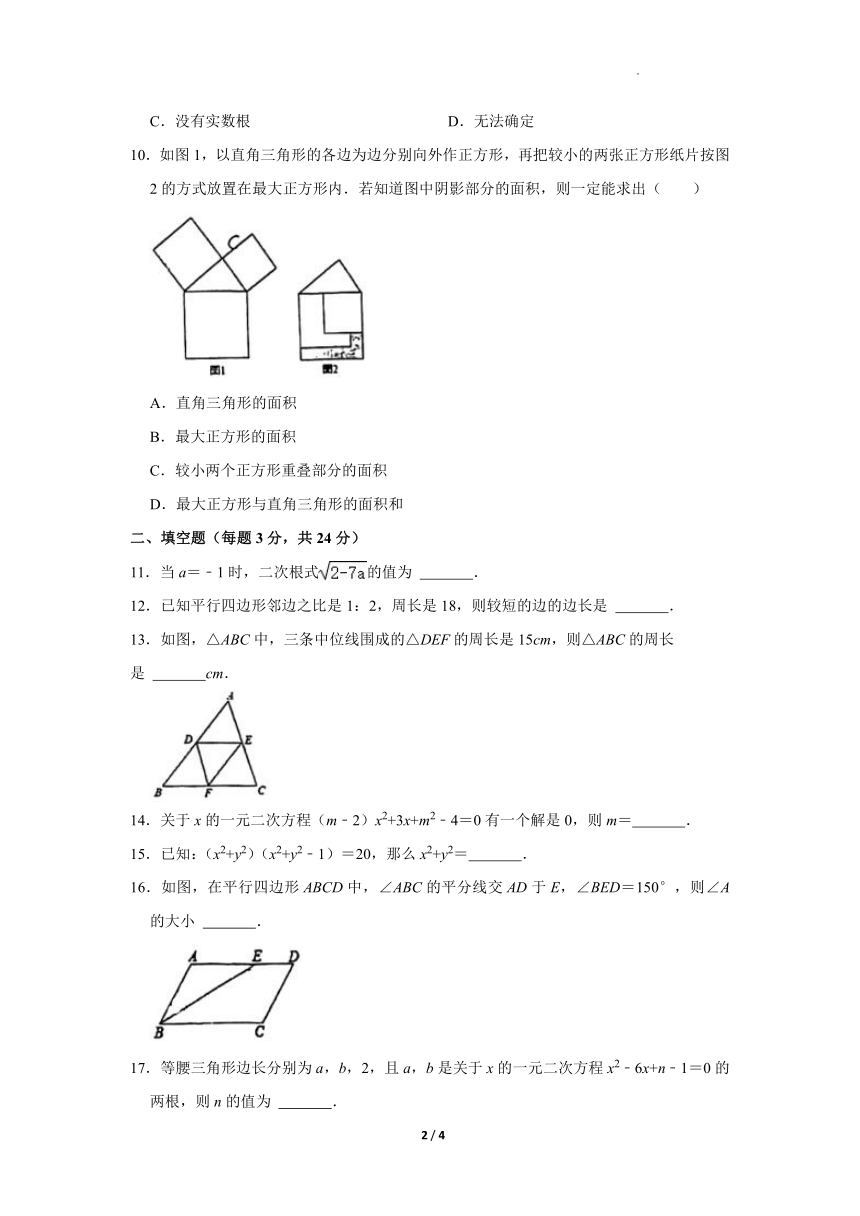
10.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
二、填空题(每题3分,共24分)
11.当a=﹣1时,二次根式的值为 .
12.已知平行四边形邻边之比是1:2,周长是18,则较短的边的边长是 .
13.如图,△ABC中,三条中位线围成的△DEF的周长是15cm,则△ABC的周长
是 cm.
14.关于x的一元二次方程(m﹣2)x2+3x+m2﹣4=0有一个解是0,则m= .
15.已知:(x2+y2)(x2+y2﹣1)=20,那么x2+y2= .
16.如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小 .
17.等腰三角形边长分别为a,b,2,且a,b是关于x的一元二次方程x2﹣6x+n﹣1=0的两根,则n的值为 .
18.如图,若将图1正方形剪成四块,恰能拼成图2的矩形,则b= a.
三、解答题第19、20题各6分,第21、22、23题各8分,第24题10分,共46分)
19.计算:(1);
(2).
20.解下列方程:
(1)x2﹣10x+16=0;
(2)2x(x﹣1)=x﹣1.
21.关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根为1,求m的值;
(3)求出以此方程两根为直角边的直角三角形的周长.
22.如图,在平行四边形ABCD中,点E,F分别是边AD,BC的中点.
(1)求证:AF=CE;
(2)若四边形AECF的周长为10,AF=3,AB=2,求平行四边形ABCD的周长.
23.为积极响应新旧动能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系.
(1)求年销售量y与销售单价x的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润,则该设备的销售单价应是多少万元?
24.如果方程x2+px+q=0满足两个实数解都为整数解,我们就称所有这样的一元二次方程为同族方程,并规定:满足G=,例如x2﹣7x+12=0有整数解3和4,所以x2﹣7x+12=0属于同族方程,所以G==.
(1)如果同族方程x2+px+q=0中有两个相等的解、我们称这个方程为同族方程中的完美方程,求证:对任意一个完美方程,总有G=4;
(2)关于x的一元二次方程kx2﹣(k﹣3)x﹣3=0属于同族方程,求整数k的值.
2 / 2
一、选择题(每小题3分,共30分)
1.下列医护图案既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.下面计算正确的是( )
A.=±5 B.÷=4 C.(﹣)2=﹣5 D.3﹣=2
3.在下列方程中,是一元二次方程的是( )
A.x2+3x= B.2(x﹣1)+x=2 C.x2=2+3x D.x2﹣x3+4=0
4.若x=2能使下列二次根式有意义,则这个二次根式可以是( )
A. B. C. D.
5.已知平行四边形ABCD中,∠A+∠C=110°,则∠B的度数为( )
A.125° B.135° C.145° D.155°
6.将一个容积为600cm3的长方体包装盒剪开、铺平,纸样如图所示,根据题意,列出关于x的方程为( )
A.15(30﹣2x) x=600 B.30(30﹣2x) x=600
C.15(15﹣x) x=600 D.x(15﹣x) x=600
7.已知a是方程x2﹣2x﹣3=0的一个根,则代数式2a2﹣4a﹣1的值为( )
A.3 B.﹣4 C.3或﹣4 D.5
8.设a=6,b=,c=+,则a,b、c的大小关系是( )
A.b>c>a B.b>a>c C.c>a>b D.a>c>b
9.当b+c=5时,关于x的一元二次方程3x2+bx﹣c=0的根的情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
10.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
二、填空题(每题3分,共24分)
11.当a=﹣1时,二次根式的值为 .
12.已知平行四边形邻边之比是1:2,周长是18,则较短的边的边长是 .
13.如图,△ABC中,三条中位线围成的△DEF的周长是15cm,则△ABC的周长
是 cm.
14.关于x的一元二次方程(m﹣2)x2+3x+m2﹣4=0有一个解是0,则m= .
15.已知:(x2+y2)(x2+y2﹣1)=20,那么x2+y2= .
16.如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小 .
17.等腰三角形边长分别为a,b,2,且a,b是关于x的一元二次方程x2﹣6x+n﹣1=0的两根,则n的值为 .
18.如图,若将图1正方形剪成四块,恰能拼成图2的矩形,则b= a.
三、解答题第19、20题各6分,第21、22、23题各8分,第24题10分,共46分)
19.计算:(1);
(2).
20.解下列方程:
(1)x2﹣10x+16=0;
(2)2x(x﹣1)=x﹣1.
21.关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根为1,求m的值;
(3)求出以此方程两根为直角边的直角三角形的周长.
22.如图,在平行四边形ABCD中,点E,F分别是边AD,BC的中点.
(1)求证:AF=CE;
(2)若四边形AECF的周长为10,AF=3,AB=2,求平行四边形ABCD的周长.
23.为积极响应新旧动能转换,提高公司经济效益,某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价x(单位:万元)成一次函数关系.
(1)求年销售量y与销售单价x的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润,则该设备的销售单价应是多少万元?
24.如果方程x2+px+q=0满足两个实数解都为整数解,我们就称所有这样的一元二次方程为同族方程,并规定:满足G=,例如x2﹣7x+12=0有整数解3和4,所以x2﹣7x+12=0属于同族方程,所以G==.
(1)如果同族方程x2+px+q=0中有两个相等的解、我们称这个方程为同族方程中的完美方程,求证:对任意一个完美方程,总有G=4;
(2)关于x的一元二次方程kx2﹣(k﹣3)x﹣3=0属于同族方程,求整数k的值.
2 / 2
同课章节目录
