鲁教版五四制九年级数学下册第一章达标检测卷(word版含答案)
文档属性
| 名称 | 鲁教版五四制九年级数学下册第一章达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 336.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 12:13:05 | ||
图片预览




文档简介
第一章达标检测卷
一、选择题(每题3分,共30分)
1.下列函数中,y是关于x的反比例函数的是( )
A.y=x B.y=4x2 C.y= D.y=-5x-1
2.已知反比例函数y=(k≠0)的图象经过点P(5,-2),则这个函数的图象位于( )
A.第一、三象限 B.第二、四象限
C.第一、二象限 D.第三、四象限
3.已知反比例函数y=,则下列描述不正确的是( )
A.图象位于第一、三象限 B.图象必经过点
C.图象不可能与坐标轴相交 D.y随x的增大而减小
4.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例函数关系.如图所示是该电路中电流I与电阻R之间的函数关系的图象,当电阻R为5 Ω时,电流I为( )
A.6 A B.5 A C.1.2 A D.1 A
5.若点A(-5,y1),B(1,y2),C(5,y3)都在反比例函数y=-的图象上,则y1,y2,y3的大小关系是( )
A.y16.在平面直角坐标系中,函数y=(x>0)与y=x-1的图象交于点P(a,b),则a+b的值为( )
A.-5 B.4 C.6 D.5
7.函数y=与y=kx+k(k为常数且k≠0)在同一平面直角坐标系中的图象可能是( )
8.设一次函数y1=-kx+b(k≠0),反比例函数y2=(k≠0).若函数y1和y2的图象仅有一个交点,则称函数y1和y2具有性质P.以下k,b的取值,使函数y1和y2具有性质P的是( )
A.k=2,b=4 B.k=3,b=4 C.k=4,b=4 D.k=5,b=4
9.如图,点A在双曲线y1=(x>0)上,点B在双曲线y2=(x<0)上,AB∥x轴,点C是x轴上一点,连接AC,BC,若△ABC的面积是6,则k的值为( )
A.-6 B.-8 C.-10 D.-12
10.如图,过反比例函数y=(k>0,x>0)图象上的四点P1,P2,P3,P4分别作x轴的垂线,垂足分别为A1,A2,A3,A4,再过点P1,P2,P3,P4分别作y轴,P1A1,P2A2,P3A3的垂线,构造了四个相邻的矩形.若这四个矩形的面积从左到右依次为S1,S2,S3,S4,OA1=A1A2=A2A3=A3A4,则S1与S4的数量关系为( )
A.S1=1.5S4 B.S1=2S4
C.S1=3S4 D.S1=4S4
二、选择题(每题4分,共24分)
11.一个反比例函数的图象过点A(1,2),则这个反比例函数的表达式是__________.
12.若反比例函数y=的图象位于第二、四象限,则k的取值范围是____________.
13.近视眼镜的度数y(度)与镜片焦距x(米)成反比例关系,已知400度近视眼镜镜片的焦距为0.25米,则近视眼镜的度数y与镜片焦距x之间的函数关系式为__________.(无需确定x的取值范围)
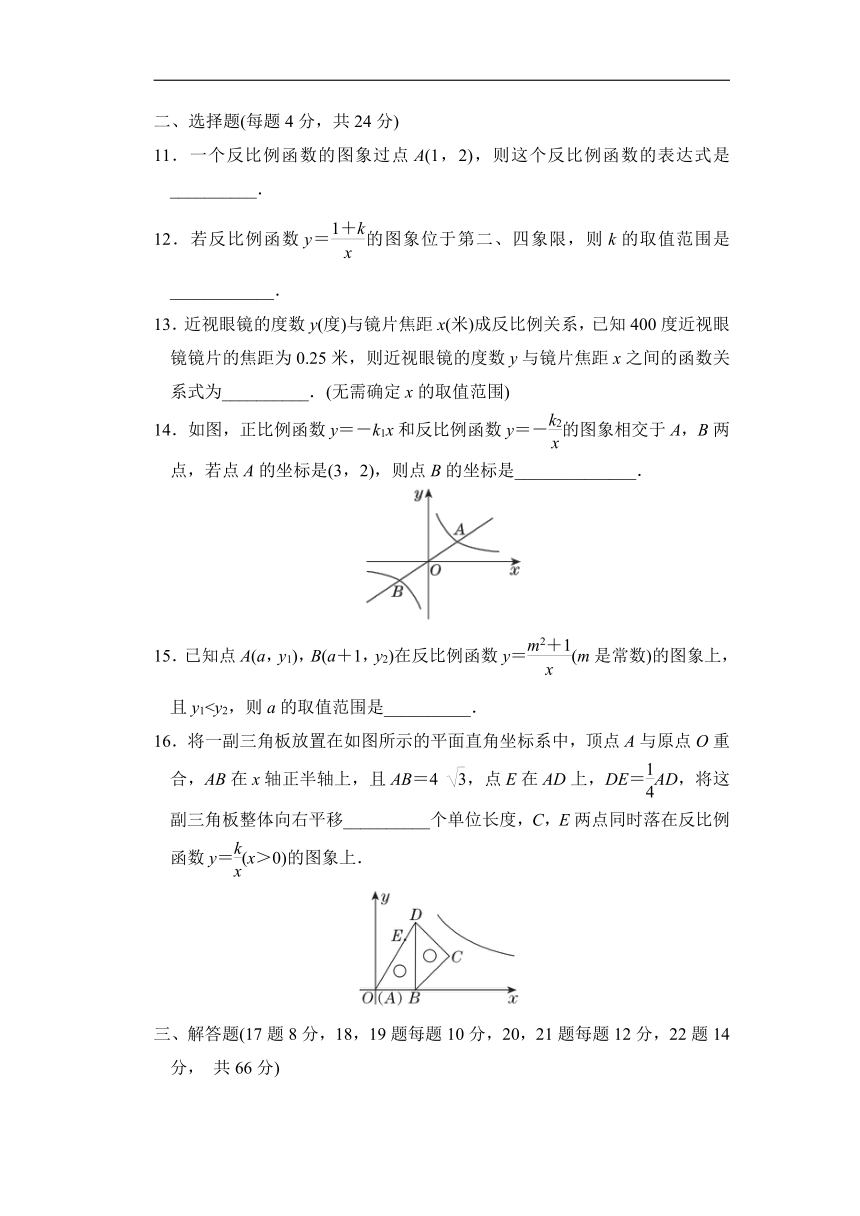
14.如图,正比例函数y=-k1x和反比例函数y=-的图象相交于A,B两点,若点A的坐标是(3,2),则点B的坐标是______________.
15.已知点A(a,y1),B(a+1,y2)在反比例函数y=(m是常数)的图象上,且y116.将一副三角板放置在如图所示的平面直角坐标系中,顶点A与原点O重合,AB在x轴正半轴上,且AB=4 ,点E在AD上,DE=AD,将这副三角板整体向右平移__________个单位长度,C,E两点同时落在反比例函数y=(x>0)的图象上.
三、解答题(17题8分,18,19题每题10分,20,21题每题12分,22题14分, 共66分)
17.已知反比例函数y=.
(1)如果这个函数的图象经过点(2,-1),求k的值;
(2)如果在这个函数图象所在的每个象限内, y的值随x值的增大而减小,求k的取值范围.
18.在平面直角坐标系xOy中,直线y=x+b与双曲线y=的一个交点为A(2,4),与y轴交于点B.
(1)求m的值和点B的坐标;
(2)点P在双曲线y=上,△OBP的面积为8,直接写出点P的坐标.
19.某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(mg)与燃烧时间x(min)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2 mg时,对人体无毒害作用.根据图象所示信息,解答下列问题:
(1)求出线段OA和双曲线的表达式;
(2)从消毒开始,至少多少分钟后,师生才能进入教室?
20.如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-的图象交于A(-2,b),B两点.
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后,与反比例函数的图象有且只有一个公共点,求m的值.
21.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在y轴、x轴上,点B的坐标为(4,2),直线y=-x+3分别交AB,BC于点M,N,反比例函数y=(x>0)的图象经过点M,N.
(1)求反比例函数的表达式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
22.如图,已知一次函数y=x-2的图象与反比例函数y=的图象相交于点A(2,n),与x轴相交于点B.
(1)求k的值以及点B的坐标;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)在y轴上是否存在点P,使PA+PB的值最小?若存在,请求出点P的坐标;若不存在,请说明理由.
答案
一、1.D 2.B 3.D 4.C 5.B 6.D
7.A 8.A 9.C
10.D 点拨:设OA1=A1A2=A2A3=A3A4=m,则OA2=2m,OA3=3m,OA4=4m.
∵点P1,P2,P3,P4都在反比例函数y=(k>0,x>0)的图象上,
∴A1P1=,A2P2=,A3P3=,A4P4=,
∴S1=OA1·A1P1=m·=k,S2=A1A2·A2P2=m·=,S3=A2A3·A3P3=m·=,S4=A3A4·A4P4=m·=,
∴S1=4S4.
二、11.y= 12.k<-1 13.y=
14.(-3,-2) 15.-116.(12-) 点拨:过点E作EN⊥DB于点N, 过点C作CM⊥BD于点M,则∠DNE=∠CMB=90°.
在Rt△ABD中,∵∠ADB=30°,AB=4 ,∴DB==12.
∵△BCD是等腰直角三角形,
∴CM=BM=DB=6,
∴点C的横坐标为4 +6,
∴C(4 +6,6) .
∵∠DNE=90°,∠DBA=90°,
∴EN∥AB,∴易得△DEN∽△DAB,
∴==.
∵DE=AD,∴EN=AB=,DN=DB=3,∴点E的横坐标为4 -=3 ,BN=12-3=9.
∴E(3 ,9).
设将这副三角板整体向右平移m个单位长度,C,E两点同时落在反比例函数y=(x>0)的图象上,
则平移后C,E两点的对应点分别为C′(4 +6+m,6),E′(3 +m,9),∴
∴(4 +6+m)×6=(3 +m)×9,解得m=12-.
经检验,m=12-是原方程的根,且符合题意.
三、17.解:(1)把点(2,-1)的坐标代入y=,得-1=,
解得k=-.
(2)∵在这个函数图象所在的每个象限内, y的值随x值的增大而减小,∴2k+1>0,解得k>-.
18.解:(1)∵双曲线y=经过点A(2,4),∴m=8.
∵直线y=x+b经过点A(2,4),
∴b=2.∴此直线与y轴的交点B的坐标为(0,2).
(2)点P的坐标为(8,1)或(-8,-1).
19.解:(1)设双曲线的表达式为y=(k≠0),将(25,6)代入上式,得k=25×6=150,
则双曲线的表达式为y=,
将y=10代入y=,得10=,解得x=15,∴A(15,10).
设直线OA的表达式为y=nx,
将A(15,10)的坐标代入上式,得n==,
则线段OA的表达式为y=x(0≤x<15),双曲线的表达式为y=(x≥15).
(2)将y=2代入y=,得2=,解得x=75.
答:从消毒开始,至少75 min后,师生才能进入教室.
20.解:(1)根据题意,把A(-2,b)的坐标分别代入一次函数和反比例函数的表达式,得
解得
∴一次函数的表达式为y=x+5.
(2)将直线AB向下平移m(m>0)个单位长度后,直线AB对应的函数表达式为y=x+5-m.
由
得x2+(5-m)x+8=0.
由题知b2-4ac=(5-m)2-4××8=0,解得m=1或m=9.
21.解:(1)由题意易得点M的纵坐标为2.将y=2代入y=-x+3,
得x=2.∴M(2,2).把点M的坐标代入y=,得k=4,
∴反比例函数的表达式是y=.
(2)由题意,得S△OPM=OP·AM.
∵S四边形BMON=S矩形OABC-S△AOM-S△CON=4×2-2-2=4,
且S△OPM=S四边形BMON,
∴OP·AM=4.
又易知AM=2,∴OP=4.
∴点P的坐标是(0,4)或(0,-4).
22.解:(1)把点A(2,n)的坐标代入y=x-2,得n=×2-2=3,
∴A(2,3).把点A(2,3)的坐标代入y=,得k=2×3=6.
令y=0,则x-2=0,解得x=,∴点B的坐标为.
(2)∵A(2,3),B,
∴AB=.
∵四边形ABCD是菱形,
∴AD=AB=,AD∥BC.
∵点C在x轴正半轴上,点D在第一象限,∴D.
(3)存在.
如图,作点B关于y轴的对称点Q,则点Q的坐标为,连接AQ交y轴于点P,连接BP,此时PA+PB的值最小.
设直线AQ的表达式为y=ax+b,
则解得
∴直线AQ的表达式为y=x+,当x=0时,y=,
∴P.
一、选择题(每题3分,共30分)
1.下列函数中,y是关于x的反比例函数的是( )
A.y=x B.y=4x2 C.y= D.y=-5x-1
2.已知反比例函数y=(k≠0)的图象经过点P(5,-2),则这个函数的图象位于( )
A.第一、三象限 B.第二、四象限
C.第一、二象限 D.第三、四象限
3.已知反比例函数y=,则下列描述不正确的是( )
A.图象位于第一、三象限 B.图象必经过点
C.图象不可能与坐标轴相交 D.y随x的增大而减小
4.某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例函数关系.如图所示是该电路中电流I与电阻R之间的函数关系的图象,当电阻R为5 Ω时,电流I为( )
A.6 A B.5 A C.1.2 A D.1 A
5.若点A(-5,y1),B(1,y2),C(5,y3)都在反比例函数y=-的图象上,则y1,y2,y3的大小关系是( )
A.y1
A.-5 B.4 C.6 D.5
7.函数y=与y=kx+k(k为常数且k≠0)在同一平面直角坐标系中的图象可能是( )
8.设一次函数y1=-kx+b(k≠0),反比例函数y2=(k≠0).若函数y1和y2的图象仅有一个交点,则称函数y1和y2具有性质P.以下k,b的取值,使函数y1和y2具有性质P的是( )
A.k=2,b=4 B.k=3,b=4 C.k=4,b=4 D.k=5,b=4
9.如图,点A在双曲线y1=(x>0)上,点B在双曲线y2=(x<0)上,AB∥x轴,点C是x轴上一点,连接AC,BC,若△ABC的面积是6,则k的值为( )
A.-6 B.-8 C.-10 D.-12
10.如图,过反比例函数y=(k>0,x>0)图象上的四点P1,P2,P3,P4分别作x轴的垂线,垂足分别为A1,A2,A3,A4,再过点P1,P2,P3,P4分别作y轴,P1A1,P2A2,P3A3的垂线,构造了四个相邻的矩形.若这四个矩形的面积从左到右依次为S1,S2,S3,S4,OA1=A1A2=A2A3=A3A4,则S1与S4的数量关系为( )
A.S1=1.5S4 B.S1=2S4
C.S1=3S4 D.S1=4S4
二、选择题(每题4分,共24分)
11.一个反比例函数的图象过点A(1,2),则这个反比例函数的表达式是__________.
12.若反比例函数y=的图象位于第二、四象限,则k的取值范围是____________.
13.近视眼镜的度数y(度)与镜片焦距x(米)成反比例关系,已知400度近视眼镜镜片的焦距为0.25米,则近视眼镜的度数y与镜片焦距x之间的函数关系式为__________.(无需确定x的取值范围)
14.如图,正比例函数y=-k1x和反比例函数y=-的图象相交于A,B两点,若点A的坐标是(3,2),则点B的坐标是______________.
15.已知点A(a,y1),B(a+1,y2)在反比例函数y=(m是常数)的图象上,且y1
三、解答题(17题8分,18,19题每题10分,20,21题每题12分,22题14分, 共66分)
17.已知反比例函数y=.
(1)如果这个函数的图象经过点(2,-1),求k的值;
(2)如果在这个函数图象所在的每个象限内, y的值随x值的增大而减小,求k的取值范围.
18.在平面直角坐标系xOy中,直线y=x+b与双曲线y=的一个交点为A(2,4),与y轴交于点B.
(1)求m的值和点B的坐标;
(2)点P在双曲线y=上,△OBP的面积为8,直接写出点P的坐标.
19.某校根据《学校卫生工作条例》,为预防“蚊虫叮咬”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(mg)与燃烧时间x(min)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),当空气中每立方米的含药量低于2 mg时,对人体无毒害作用.根据图象所示信息,解答下列问题:
(1)求出线段OA和双曲线的表达式;
(2)从消毒开始,至少多少分钟后,师生才能进入教室?
20.如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-的图象交于A(-2,b),B两点.
(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后,与反比例函数的图象有且只有一个公共点,求m的值.
21.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在y轴、x轴上,点B的坐标为(4,2),直线y=-x+3分别交AB,BC于点M,N,反比例函数y=(x>0)的图象经过点M,N.
(1)求反比例函数的表达式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
22.如图,已知一次函数y=x-2的图象与反比例函数y=的图象相交于点A(2,n),与x轴相交于点B.
(1)求k的值以及点B的坐标;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)在y轴上是否存在点P,使PA+PB的值最小?若存在,请求出点P的坐标;若不存在,请说明理由.
答案
一、1.D 2.B 3.D 4.C 5.B 6.D
7.A 8.A 9.C
10.D 点拨:设OA1=A1A2=A2A3=A3A4=m,则OA2=2m,OA3=3m,OA4=4m.
∵点P1,P2,P3,P4都在反比例函数y=(k>0,x>0)的图象上,
∴A1P1=,A2P2=,A3P3=,A4P4=,
∴S1=OA1·A1P1=m·=k,S2=A1A2·A2P2=m·=,S3=A2A3·A3P3=m·=,S4=A3A4·A4P4=m·=,
∴S1=4S4.
二、11.y= 12.k<-1 13.y=
14.(-3,-2) 15.-1
在Rt△ABD中,∵∠ADB=30°,AB=4 ,∴DB==12.
∵△BCD是等腰直角三角形,
∴CM=BM=DB=6,
∴点C的横坐标为4 +6,
∴C(4 +6,6) .
∵∠DNE=90°,∠DBA=90°,
∴EN∥AB,∴易得△DEN∽△DAB,
∴==.
∵DE=AD,∴EN=AB=,DN=DB=3,∴点E的横坐标为4 -=3 ,BN=12-3=9.
∴E(3 ,9).
设将这副三角板整体向右平移m个单位长度,C,E两点同时落在反比例函数y=(x>0)的图象上,
则平移后C,E两点的对应点分别为C′(4 +6+m,6),E′(3 +m,9),∴
∴(4 +6+m)×6=(3 +m)×9,解得m=12-.
经检验,m=12-是原方程的根,且符合题意.
三、17.解:(1)把点(2,-1)的坐标代入y=,得-1=,
解得k=-.
(2)∵在这个函数图象所在的每个象限内, y的值随x值的增大而减小,∴2k+1>0,解得k>-.
18.解:(1)∵双曲线y=经过点A(2,4),∴m=8.
∵直线y=x+b经过点A(2,4),
∴b=2.∴此直线与y轴的交点B的坐标为(0,2).
(2)点P的坐标为(8,1)或(-8,-1).
19.解:(1)设双曲线的表达式为y=(k≠0),将(25,6)代入上式,得k=25×6=150,
则双曲线的表达式为y=,
将y=10代入y=,得10=,解得x=15,∴A(15,10).
设直线OA的表达式为y=nx,
将A(15,10)的坐标代入上式,得n==,
则线段OA的表达式为y=x(0≤x<15),双曲线的表达式为y=(x≥15).
(2)将y=2代入y=,得2=,解得x=75.
答:从消毒开始,至少75 min后,师生才能进入教室.
20.解:(1)根据题意,把A(-2,b)的坐标分别代入一次函数和反比例函数的表达式,得
解得
∴一次函数的表达式为y=x+5.
(2)将直线AB向下平移m(m>0)个单位长度后,直线AB对应的函数表达式为y=x+5-m.
由
得x2+(5-m)x+8=0.
由题知b2-4ac=(5-m)2-4××8=0,解得m=1或m=9.
21.解:(1)由题意易得点M的纵坐标为2.将y=2代入y=-x+3,
得x=2.∴M(2,2).把点M的坐标代入y=,得k=4,
∴反比例函数的表达式是y=.
(2)由题意,得S△OPM=OP·AM.
∵S四边形BMON=S矩形OABC-S△AOM-S△CON=4×2-2-2=4,
且S△OPM=S四边形BMON,
∴OP·AM=4.
又易知AM=2,∴OP=4.
∴点P的坐标是(0,4)或(0,-4).
22.解:(1)把点A(2,n)的坐标代入y=x-2,得n=×2-2=3,
∴A(2,3).把点A(2,3)的坐标代入y=,得k=2×3=6.
令y=0,则x-2=0,解得x=,∴点B的坐标为.
(2)∵A(2,3),B,
∴AB=.
∵四边形ABCD是菱形,
∴AD=AB=,AD∥BC.
∵点C在x轴正半轴上,点D在第一象限,∴D.
(3)存在.
如图,作点B关于y轴的对称点Q,则点Q的坐标为,连接AQ交y轴于点P,连接BP,此时PA+PB的值最小.
设直线AQ的表达式为y=ax+b,
则解得
∴直线AQ的表达式为y=x+,当x=0时,y=,
∴P.
