北师大版八下1.4.2 角平分线 课件(共16张PPT)
文档属性
| 名称 | 北师大版八下1.4.2 角平分线 课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 567.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 16:09:26 | ||
图片预览



文档简介
(共16张PPT)
第一章 三角形的证明
4.2 角平分线
北师大版八年级数学下册
崇德尚礼 笃学求真
学习&目标
1.会证明和运用“三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等”.(重点)
2.经历探索、猜想、证明的过程,进一步发展学生的推理证明意识和能力.(难点)
情境&导入
三条笔直的公路围成一个三角形区域,现在计划在这个区域内修建一个仓库P,使P到三条公路的距离都相等,请在三角形区域内标出仓库P的位置.
探索&交流
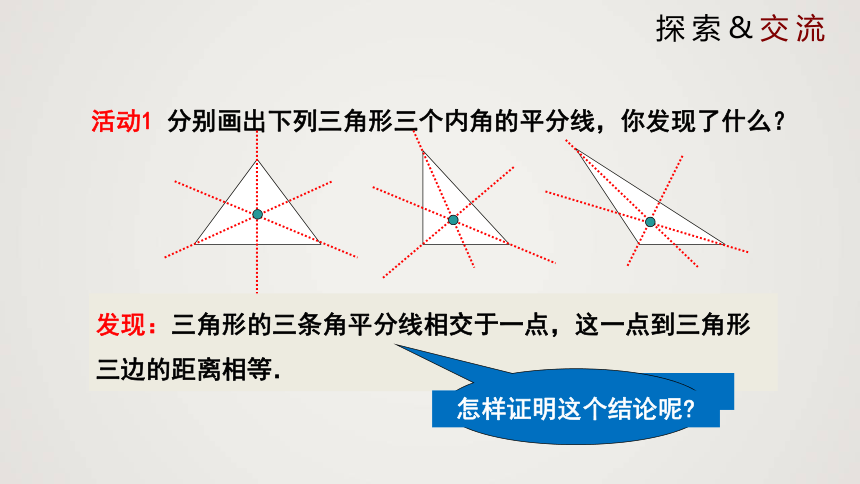
活动1 分别画出下列三角形三个内角的平分线,你发现了什么?
发现:三角形的三条角平分线相交于一点,这一点到三角形三边的距离相等.
怎样证明这个结论呢
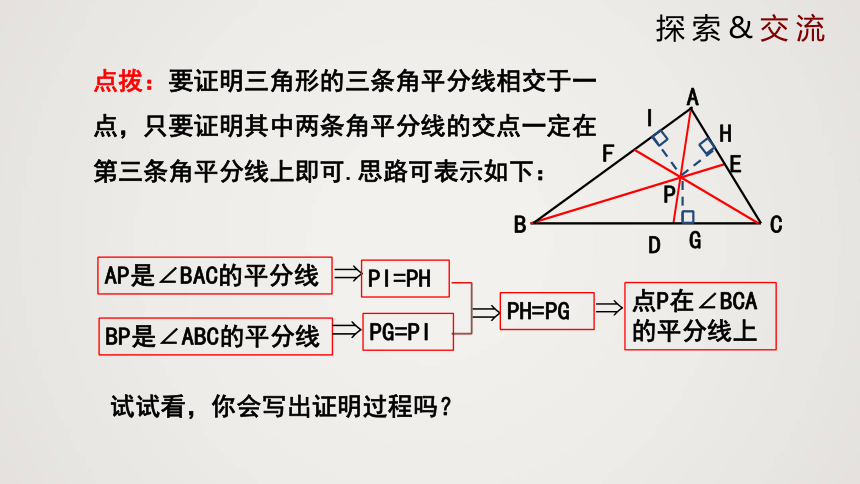
点拨:要证明三角形的三条角平分线相交于一点,只要证明其中两条角平分线的交点一定在第三条角平分线上即可.思路可表示如下:
试试看,你会写出证明过程吗?
AP是∠BAC的平分线
BP是∠ABC的平分线
PI=PH
PG=PI
PH=PG
点P在∠BCA的平分线上
A
B
C
P
F
H
D
E
I
G
探索&交流
探索&交流
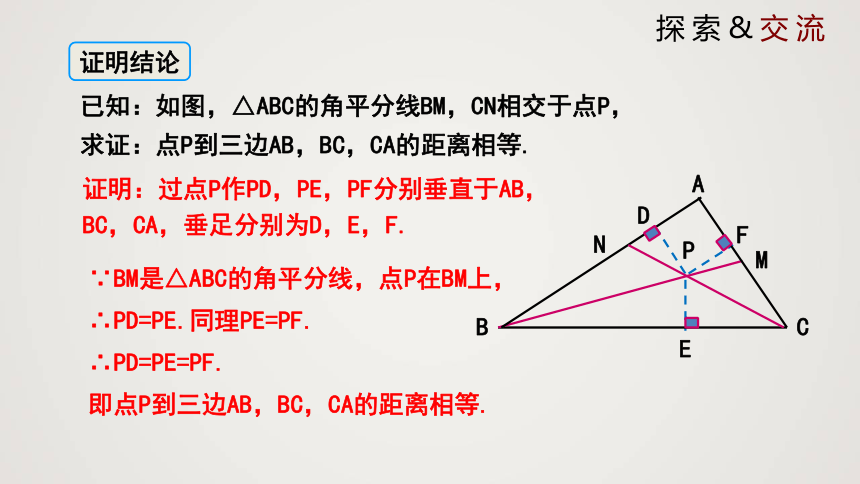
已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
证明结论
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
探索&交流
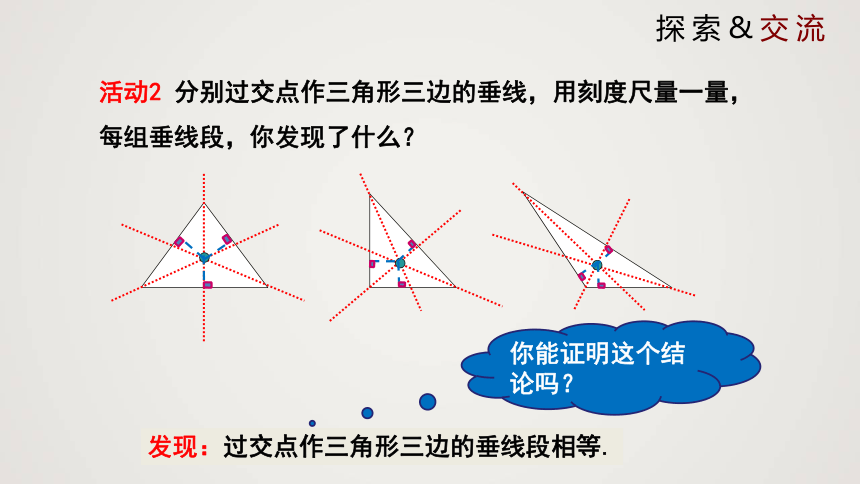
活动2 分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等.
你能证明这个结论吗?
探索&交流
三边垂直平分线 三条角平分线
三角形 锐角三角形 交于三角形内一点 交于三角形内一点
钝角三角形 交于三角形外一点
直角三角形 交于斜边的中点
交点性质 到三角形三个顶点的距离相等 到三角形三边的距离相等
归纳总结
例题&解析
例题欣赏
例1.如图,在△ABC中,已知AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD=4cm,AC的长;
(2)求证:AB=AC+CD.
E
D
A
B
C
(1)解:∵AD是△ABC的角平分线,DE⊥AB,垂足为E,
∴DE=CD=4cm.
∵AC=BC,∴∠B=∠BAC.
∵∠C=90°,∴∠B=45°.∴BE=DE.
在等腰直角三角形BDE中,
(2)证明:由(1)的求解过程易知,
Rt△ACD≌Rt△AED(HL).
∴AC=AE.
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
例题&解析
例题&解析
例题欣赏
M
E
N
A
B
C
P
O
D
例2.如图,在直角△ABC中,AC=BC,∠C=90°,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4,
(1)求点O到△ABC三边的距离和.
(2)若△ABC的周长为32,求△ABC的面积.
12
例题&解析
解:连接OC
练习&巩固
1. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC 的三条中线的交点
B.△ABC 三边的中垂线的交点
C.△ABC 三条角平分线的交点
D.△ABC 三条高所在直线的交点
练习&巩固
2.如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )
A.110°
B.120°
C.130°
D.140°
练习&巩固
3.已知:如图,在 Rt△ACB 中,∠ACB =90°,∠B=40°, AD平分∠CAB 交BC于D点, DE⊥AB于E,则∠CAD = ________.
A
C
B
D
E
小结&反思
三角形内角平分线的性质
性质:三角形的三条角平分线交于一点,并且这一点到三条边的距离相等
用途:位置选择
可以用来选取到三条直线距离相等的点
第一章 三角形的证明
4.2 角平分线
北师大版八年级数学下册
崇德尚礼 笃学求真
学习&目标
1.会证明和运用“三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等”.(重点)
2.经历探索、猜想、证明的过程,进一步发展学生的推理证明意识和能力.(难点)
情境&导入
三条笔直的公路围成一个三角形区域,现在计划在这个区域内修建一个仓库P,使P到三条公路的距离都相等,请在三角形区域内标出仓库P的位置.
探索&交流
活动1 分别画出下列三角形三个内角的平分线,你发现了什么?
发现:三角形的三条角平分线相交于一点,这一点到三角形三边的距离相等.
怎样证明这个结论呢
点拨:要证明三角形的三条角平分线相交于一点,只要证明其中两条角平分线的交点一定在第三条角平分线上即可.思路可表示如下:
试试看,你会写出证明过程吗?
AP是∠BAC的平分线
BP是∠ABC的平分线
PI=PH
PG=PI
PH=PG
点P在∠BCA的平分线上
A
B
C
P
F
H
D
E
I
G
探索&交流
探索&交流
已知:如图,△ABC的角平分线BM,CN相交于点P,
求证:点P到三边AB,BC,CA的距离相等.
证明结论
证明:过点P作PD,PE,PF分别垂直于AB,BC,CA,垂足分别为D,E,F.
∵BM是△ABC的角平分线,点P在BM上,
∴PD=PE.同理PE=PF.
∴PD=PE=PF.
即点P到三边AB,BC,CA的距离相等.
D
E
F
A
B
C
P
N
M
探索&交流
活动2 分别过交点作三角形三边的垂线,用刻度尺量一量,每组垂线段,你发现了什么?
发现:过交点作三角形三边的垂线段相等.
你能证明这个结论吗?
探索&交流
三边垂直平分线 三条角平分线
三角形 锐角三角形 交于三角形内一点 交于三角形内一点
钝角三角形 交于三角形外一点
直角三角形 交于斜边的中点
交点性质 到三角形三个顶点的距离相等 到三角形三边的距离相等
归纳总结
例题&解析
例题欣赏
例1.如图,在△ABC中,已知AC=BC, ∠C=90°, AD是△ABC的角平分线,DE⊥AB,垂足为E.
(1)如果CD=4cm,AC的长;
(2)求证:AB=AC+CD.
E
D
A
B
C
(1)解:∵AD是△ABC的角平分线,DE⊥AB,垂足为E,
∴DE=CD=4cm.
∵AC=BC,∴∠B=∠BAC.
∵∠C=90°,∴∠B=45°.∴BE=DE.
在等腰直角三角形BDE中,
(2)证明:由(1)的求解过程易知,
Rt△ACD≌Rt△AED(HL).
∴AC=AE.
∵BE=DE=CD,
∴AB=AE+BE=AC+CD.
例题&解析
例题&解析
例题欣赏
M
E
N
A
B
C
P
O
D
例2.如图,在直角△ABC中,AC=BC,∠C=90°,AP平分∠BAC,BD平分∠ABC;AP,BD交于点O,过点O作OM⊥AC,若OM=4,
(1)求点O到△ABC三边的距离和.
(2)若△ABC的周长为32,求△ABC的面积.
12
例题&解析
解:连接OC
练习&巩固
1. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC 的三条中线的交点
B.△ABC 三边的中垂线的交点
C.△ABC 三条角平分线的交点
D.△ABC 三条高所在直线的交点
练习&巩固
2.如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等.若∠A=40°,则∠BOC的度数为( )
A.110°
B.120°
C.130°
D.140°
练习&巩固
3.已知:如图,在 Rt△ACB 中,∠ACB =90°,∠B=40°, AD平分∠CAB 交BC于D点, DE⊥AB于E,则∠CAD = ________.
A
C
B
D
E
小结&反思
三角形内角平分线的性质
性质:三角形的三条角平分线交于一点,并且这一点到三条边的距离相等
用途:位置选择
可以用来选取到三条直线距离相等的点
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
