2021—2022学年北师大版八年级数学下册1.1等腰三角形知识点过关练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年北师大版八年级数学下册1.1等腰三角形知识点过关练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 452.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 12:20:53 | ||
图片预览




文档简介
北师大版八年级数学下册知识点过关练习
(1.1《等腰三角形》专题)
时间:90分钟 总分:100分
选择题(40分).
题号 1 2 3 4 5 6 7 8 9 10
选项
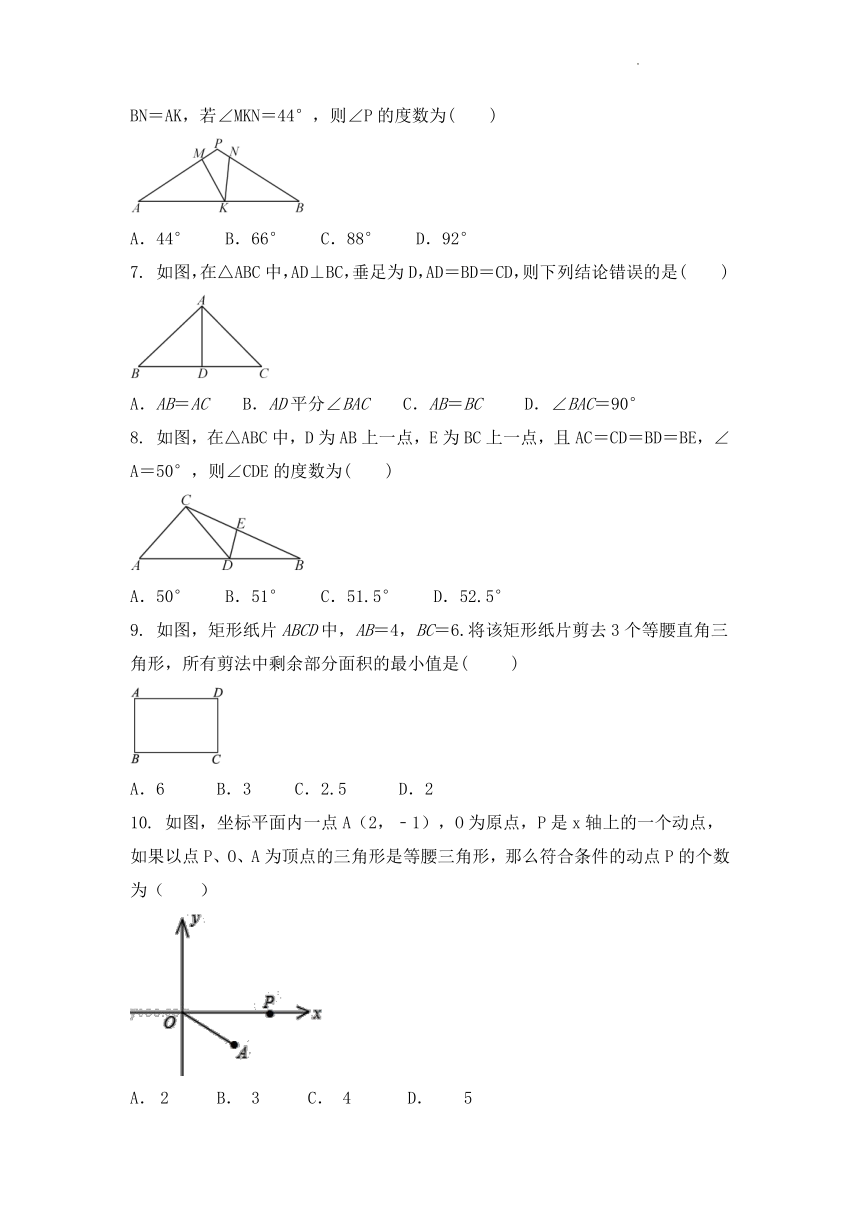
1.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A. BD=CE B. AD=AE C. DA=DE D. BE=CD
2. 如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
3.等腰三角形的一个角是80°,则它顶角的度数是( )
A. 80° B.80°或20° C. 80°或50° D. 20°
4. 如图,在△ABC中,AB=AC,AD平分∠BAC,则下列结论错误的是( )
A.∠B=∠C B.AD⊥BC
C.∠BAD=∠CAD=∠C D.BD=CD
5. 已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是( )
A. 20或16 B.20 C.16 D.以上答案均不对
6. 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44° B.66° C.88° D.92°
7. 如图,在△ABC中,AD⊥BC,垂足为D,AD=BD=CD,则下列结论错误的是( )
A.AB=AC B.AD平分∠BAC C.AB=BC D.∠BAC=90°
8. 如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
A.50° B.51° C.51.5° D.52.5°
9. 如图,矩形纸片ABCD中,AB=4,BC=6.将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( )
A.6 B.3 C.2.5 D.2
10. 如图,坐标平面内一点A(2,﹣1),O为原点,P是x轴上的一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,那么符合条件的动点P的个数为( )
A. 2 B. 3 C. 4 D. 5
二、填空题(20分)。
11.如图,在△ABC中,∠1=∠2,BE=CD,AB=5,AE=2,则CE=____.
12. 如图,已知AB∥CD,AB=AC,∠ABC=68°,则∠ACD= __ .
13.如图,在△ABC中,AB=AC,∠A=80°,E,F,P分别是AB,AC,BC边上一点,且BE=BP,CP=CF,则∠EPF=___ 度.
14. 若三角形三边长满足(a﹣b)(a﹣c)=0,则△ABC的形状是 __ .
15.如图钢架中,焊上等长的13根钢条来加固钢架.若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是____.
三、解答题(40分)。
16. 如图,△ABC中,∠A=36°,AB=AC,CD平分∠ACB,试说明△BCD是等腰三角形.
17. 如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB.AE=CE,求证:
(1)△AEF≌△CEB;
(2)AF=2CD.
18. 如图,AB=AE,BC=DE,∠B=∠E,点F是CD的中点. 求证:AF⊥CD.
19. 如图,在△ABC中,AB=AC,∠BAC=90°,BD是∠ABC的平分线,CE⊥BD,垂足是E,BA和CE的延长线交于点F.
(1) 在图中找出与△ABD全等的三角形,并证明你的结论;
(2) 证明:BD=2EC.
20.(1)如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,分别交AB、AC于点D、E.判断DE=DB+EC是否成立?为什么?
(2)如图,若点F是∠ABC的平分线和外角∠ACG的平分线的交点,其他条件不变,请猜想线段DE、DB、EC之间有何数量关系?证明你的猜想.
北师大版八年级数学下册知识点过关练习
(1.1《等腰三角形》专题)
时间:90分钟 总分:100分
选择题(40分).
题号 1 2 3 4 5 6 7 8 9 10
选项
1.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( C )
A. BD=CE B. AD=AE C. DA=DE D. BE=CD
2. 如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( A )
A.35° B.40° C.45° D.50°
3.等腰三角形的一个角是80°,则它顶角的度数是( B )
A. 80° B.80°或20° C. 80°或50° D. 20°
4. 如图,在△ABC中,AB=AC,AD平分∠BAC,则下列结论错误的是( C )
A.∠B=∠C B.AD⊥BC
C.∠BAD=∠CAD=∠C D.BD=CD
5. 已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是( B )
A. 20或16 B.20 C.16 D.以上答案均不对
6. 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( D )
A.44° B.66° C.88° D.92°
7. 如图,在△ABC中,AD⊥BC,垂足为D,AD=BD=CD,则下列结论错误的是( C )
A.AB=AC B.AD平分∠BAC C.AB=BC D.∠BAC=90°
8. 如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( D )
A.50° B.51° C.51.5° D.52.5°
9. 如图,矩形纸片ABCD中,AB=4,BC=6.将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( C )
A.6 B.3 C.2.5 D.2
10. 如图,坐标平面内一点A(2,﹣1),O为原点,P是x轴上的一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,那么符合条件的动点P的个数为( B )
A. 2 B. 3 C. 4 D. 5
二、填空题(20分)。
11.如图,在△ABC中,∠1=∠2,BE=CD,AB=5,AE=2,则CE=__3__.
12. 如图,已知AB∥CD,AB=AC,∠ABC=68°,则∠ACD= __44° .
13.如图,在△ABC中,AB=AC,∠A=80°,E,F,P分别是AB,AC,BC边上一点,且BE=BP,CP=CF,则∠EPF=__50_ 度.
14. 若三角形三边长满足(a﹣b)(a﹣c)=0,则△ABC的形状是 等腰三角形__ .
15.如图钢架中,焊上等长的13根钢条来加固钢架.若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是__12°__.
三、解答题(40分)。
16. 如图,△ABC中,∠A=36°,AB=AC,CD平分∠ACB,试说明△BCD是等腰三角形.
解:在△ABC中
∵AB=AC,∠A=36°
∴∠B=∠ACB=(180°﹣∠A)=72°
∵CD平分∠ACB
∴∠DCB=∠ACB=36°
在△DBC中
∠BDC=180°﹣∠B﹣∠DCB=72°=∠B
∴CD=CB
即△BCD是等腰三角形.
17. 如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB.AE=CE,求证:
(1)△AEF≌△CEB;
(2)AF=2CD.
证明:(1)∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD.
18. 如图,AB=AE,BC=DE,∠B=∠E,点F是CD的中点. 求证:AF⊥CD.
证明:如图,连接AC,AD,
在△ABC和△AED中,
∴△ABC≌△AED(SAS),
∴AC=AD,
∵点F是CD的中点,
∴AF⊥CD.
19. 如图,在△ABC中,AB=AC,∠BAC=90°,BD是∠ABC的平分线,CE⊥BD,垂足是E,BA和CE的延长线交于点F.
(1) 在图中找出与△ABD全等的三角形,并证明你的结论;
(2) 证明:BD=2EC.
证明:(1)△ABD≌△ACF.
∵AB=AC,∠BAC=90°,
∴∠FAC=∠BAC=90°,
∵BD⊥CE,∠BAC=90°,
∴∠ADB=∠EDC,
∴∠ABD=∠ACF,
∵在△ABD和△ACF中,
∴△ABD≌△ACF(ASA).
(2)∵△ABD≌△ACF,
∴BD=CF,
∵BD⊥CE,
∴∠BEF=∠BEC,
∵BD是∠ABC的平分线,
∴∠FBE=∠CBE,
∵在△FBE和△CBE中,
∴△FBE≌△CBE(ASA),
∴EF=EC,
∴CF=2CE,
∴BD=2CE.
20.(1)如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,分别交AB、AC于点D、E.判断DE=DB+EC是否成立?为什么?
(2)如图,若点F是∠ABC的平分线和外角∠ACG的平分线的交点,其他条件不变,请猜想线段DE、DB、EC之间有何数量关系?证明你的猜想.
解:(1)成立;
∵△ABC中BF、CF平分∠ABC、∠ACB,
∴∠1=∠2,∠5=∠4.
∵DE∥BC,∴∠2=∠3,∠4=∠6.
∴∠1=∠3,∠6=∠5.
根据在同一个三角形中,等角对等边的性质,可知:BD=DF,EF=CE.
∴DE=DF+EF=BD+CE.
故成立.
(2)∵BF分∠ABC,
∴∠DBF=∠FBC.
∵DF∥BC,∴∠DFB=∠FBC.
∴∠ABF=∠DFB,
∴BD=DF.
∵CF平分∠ACG,
∴∠ACF=∠FCG.
∵DF∥BC,
∴∠DFC=∠FCG.
∴∠ACF=∠DFC,
∴CE=EF.
∵EF+DE=DF,即DE+EC=BD.
(1.1《等腰三角形》专题)
时间:90分钟 总分:100分
选择题(40分).
题号 1 2 3 4 5 6 7 8 9 10
选项
1.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A. BD=CE B. AD=AE C. DA=DE D. BE=CD
2. 如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( )
A.35° B.40° C.45° D.50°
3.等腰三角形的一个角是80°,则它顶角的度数是( )
A. 80° B.80°或20° C. 80°或50° D. 20°
4. 如图,在△ABC中,AB=AC,AD平分∠BAC,则下列结论错误的是( )
A.∠B=∠C B.AD⊥BC
C.∠BAD=∠CAD=∠C D.BD=CD
5. 已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是( )
A. 20或16 B.20 C.16 D.以上答案均不对
6. 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44° B.66° C.88° D.92°
7. 如图,在△ABC中,AD⊥BC,垂足为D,AD=BD=CD,则下列结论错误的是( )
A.AB=AC B.AD平分∠BAC C.AB=BC D.∠BAC=90°
8. 如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )
A.50° B.51° C.51.5° D.52.5°
9. 如图,矩形纸片ABCD中,AB=4,BC=6.将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( )
A.6 B.3 C.2.5 D.2
10. 如图,坐标平面内一点A(2,﹣1),O为原点,P是x轴上的一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,那么符合条件的动点P的个数为( )
A. 2 B. 3 C. 4 D. 5
二、填空题(20分)。
11.如图,在△ABC中,∠1=∠2,BE=CD,AB=5,AE=2,则CE=____.
12. 如图,已知AB∥CD,AB=AC,∠ABC=68°,则∠ACD= __ .
13.如图,在△ABC中,AB=AC,∠A=80°,E,F,P分别是AB,AC,BC边上一点,且BE=BP,CP=CF,则∠EPF=___ 度.
14. 若三角形三边长满足(a﹣b)(a﹣c)=0,则△ABC的形状是 __ .
15.如图钢架中,焊上等长的13根钢条来加固钢架.若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是____.
三、解答题(40分)。
16. 如图,△ABC中,∠A=36°,AB=AC,CD平分∠ACB,试说明△BCD是等腰三角形.
17. 如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB.AE=CE,求证:
(1)△AEF≌△CEB;
(2)AF=2CD.
18. 如图,AB=AE,BC=DE,∠B=∠E,点F是CD的中点. 求证:AF⊥CD.
19. 如图,在△ABC中,AB=AC,∠BAC=90°,BD是∠ABC的平分线,CE⊥BD,垂足是E,BA和CE的延长线交于点F.
(1) 在图中找出与△ABD全等的三角形,并证明你的结论;
(2) 证明:BD=2EC.
20.(1)如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,分别交AB、AC于点D、E.判断DE=DB+EC是否成立?为什么?
(2)如图,若点F是∠ABC的平分线和外角∠ACG的平分线的交点,其他条件不变,请猜想线段DE、DB、EC之间有何数量关系?证明你的猜想.
北师大版八年级数学下册知识点过关练习
(1.1《等腰三角形》专题)
时间:90分钟 总分:100分
选择题(40分).
题号 1 2 3 4 5 6 7 8 9 10
选项
1.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( C )
A. BD=CE B. AD=AE C. DA=DE D. BE=CD
2. 如图,在△ABC中,AB=AD=DC,∠B=70°,则∠C的度数为( A )
A.35° B.40° C.45° D.50°
3.等腰三角形的一个角是80°,则它顶角的度数是( B )
A. 80° B.80°或20° C. 80°或50° D. 20°
4. 如图,在△ABC中,AB=AC,AD平分∠BAC,则下列结论错误的是( C )
A.∠B=∠C B.AD⊥BC
C.∠BAD=∠CAD=∠C D.BD=CD
5. 已知实数x,y满足,则以x,y的值为两边长的等腰三角形的周长是( B )
A. 20或16 B.20 C.16 D.以上答案均不对
6. 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( D )
A.44° B.66° C.88° D.92°
7. 如图,在△ABC中,AD⊥BC,垂足为D,AD=BD=CD,则下列结论错误的是( C )
A.AB=AC B.AD平分∠BAC C.AB=BC D.∠BAC=90°
8. 如图,在△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( D )
A.50° B.51° C.51.5° D.52.5°
9. 如图,矩形纸片ABCD中,AB=4,BC=6.将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( C )
A.6 B.3 C.2.5 D.2
10. 如图,坐标平面内一点A(2,﹣1),O为原点,P是x轴上的一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,那么符合条件的动点P的个数为( B )
A. 2 B. 3 C. 4 D. 5
二、填空题(20分)。
11.如图,在△ABC中,∠1=∠2,BE=CD,AB=5,AE=2,则CE=__3__.
12. 如图,已知AB∥CD,AB=AC,∠ABC=68°,则∠ACD= __44° .
13.如图,在△ABC中,AB=AC,∠A=80°,E,F,P分别是AB,AC,BC边上一点,且BE=BP,CP=CF,则∠EPF=__50_ 度.
14. 若三角形三边长满足(a﹣b)(a﹣c)=0,则△ABC的形状是 等腰三角形__ .
15.如图钢架中,焊上等长的13根钢条来加固钢架.若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是__12°__.
三、解答题(40分)。
16. 如图,△ABC中,∠A=36°,AB=AC,CD平分∠ACB,试说明△BCD是等腰三角形.
解:在△ABC中
∵AB=AC,∠A=36°
∴∠B=∠ACB=(180°﹣∠A)=72°
∵CD平分∠ACB
∴∠DCB=∠ACB=36°
在△DBC中
∠BDC=180°﹣∠B﹣∠DCB=72°=∠B
∴CD=CB
即△BCD是等腰三角形.
17. 如图,在△ABC中,AB=AC,AD⊥BC,CE⊥AB.AE=CE,求证:
(1)△AEF≌△CEB;
(2)AF=2CD.
证明:(1)∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD.
18. 如图,AB=AE,BC=DE,∠B=∠E,点F是CD的中点. 求证:AF⊥CD.
证明:如图,连接AC,AD,
在△ABC和△AED中,
∴△ABC≌△AED(SAS),
∴AC=AD,
∵点F是CD的中点,
∴AF⊥CD.
19. 如图,在△ABC中,AB=AC,∠BAC=90°,BD是∠ABC的平分线,CE⊥BD,垂足是E,BA和CE的延长线交于点F.
(1) 在图中找出与△ABD全等的三角形,并证明你的结论;
(2) 证明:BD=2EC.
证明:(1)△ABD≌△ACF.
∵AB=AC,∠BAC=90°,
∴∠FAC=∠BAC=90°,
∵BD⊥CE,∠BAC=90°,
∴∠ADB=∠EDC,
∴∠ABD=∠ACF,
∵在△ABD和△ACF中,
∴△ABD≌△ACF(ASA).
(2)∵△ABD≌△ACF,
∴BD=CF,
∵BD⊥CE,
∴∠BEF=∠BEC,
∵BD是∠ABC的平分线,
∴∠FBE=∠CBE,
∵在△FBE和△CBE中,
∴△FBE≌△CBE(ASA),
∴EF=EC,
∴CF=2CE,
∴BD=2CE.
20.(1)如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,分别交AB、AC于点D、E.判断DE=DB+EC是否成立?为什么?
(2)如图,若点F是∠ABC的平分线和外角∠ACG的平分线的交点,其他条件不变,请猜想线段DE、DB、EC之间有何数量关系?证明你的猜想.
解:(1)成立;
∵△ABC中BF、CF平分∠ABC、∠ACB,
∴∠1=∠2,∠5=∠4.
∵DE∥BC,∴∠2=∠3,∠4=∠6.
∴∠1=∠3,∠6=∠5.
根据在同一个三角形中,等角对等边的性质,可知:BD=DF,EF=CE.
∴DE=DF+EF=BD+CE.
故成立.
(2)∵BF分∠ABC,
∴∠DBF=∠FBC.
∵DF∥BC,∴∠DFB=∠FBC.
∴∠ABF=∠DFB,
∴BD=DF.
∵CF平分∠ACG,
∴∠ACF=∠FCG.
∵DF∥BC,
∴∠DFC=∠FCG.
∴∠ACF=∠DFC,
∴CE=EF.
∵EF+DE=DF,即DE+EC=BD.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
