2021-2022学年华东师大版九年级数学下册第28章样本与总体单元复习训练卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学下册第28章样本与总体单元复习训练卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 366.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 12:20:52 | ||
图片预览



文档简介
华东师大版九年级数学下册
第28章 样本与总体
单元复习训练卷
一、选择题(共10小题,4*10=40)
1. 为了了解某校学生的每日运动量,收集数据正确的是( )
A.调查学校舞蹈队学生每日的运动量
B.调查学校书法小组学生每日的运动量
C.调查学校田径队学生每日的运动量
D.从校七、八、九年级各随机抽取20名学生,调查学生每日的运动量
2. 为了了解某市九年级学生学业水平考试的数学成绩,从中随机抽取1000名学生的数学成绩,下列说法正确的是( )
A.某市九年级学生是总体
B.每一名九年级学生是个体
C.1000名九年级学生是总体的一个样本
D.样本容量是1000
3. 为了解某市参加中考的15000名学生的视力情况,抽取1000名学生的视力进行统计分析,下列判断错误的是( )
A.15000名学生的视力是总体
B.1000名学生是总体的一个样本
C.每名学生的视力是总体的一个个体
D.样本容量为1000
4. 下列调查不适合用简单随机抽样的是( )
A.检查一批罐头的质量是否合格
B.了解一批炮弹的杀伤力
C.调查英文26个字母中使用频率最大的字母
D.了解一个班某次数学考试的平均分
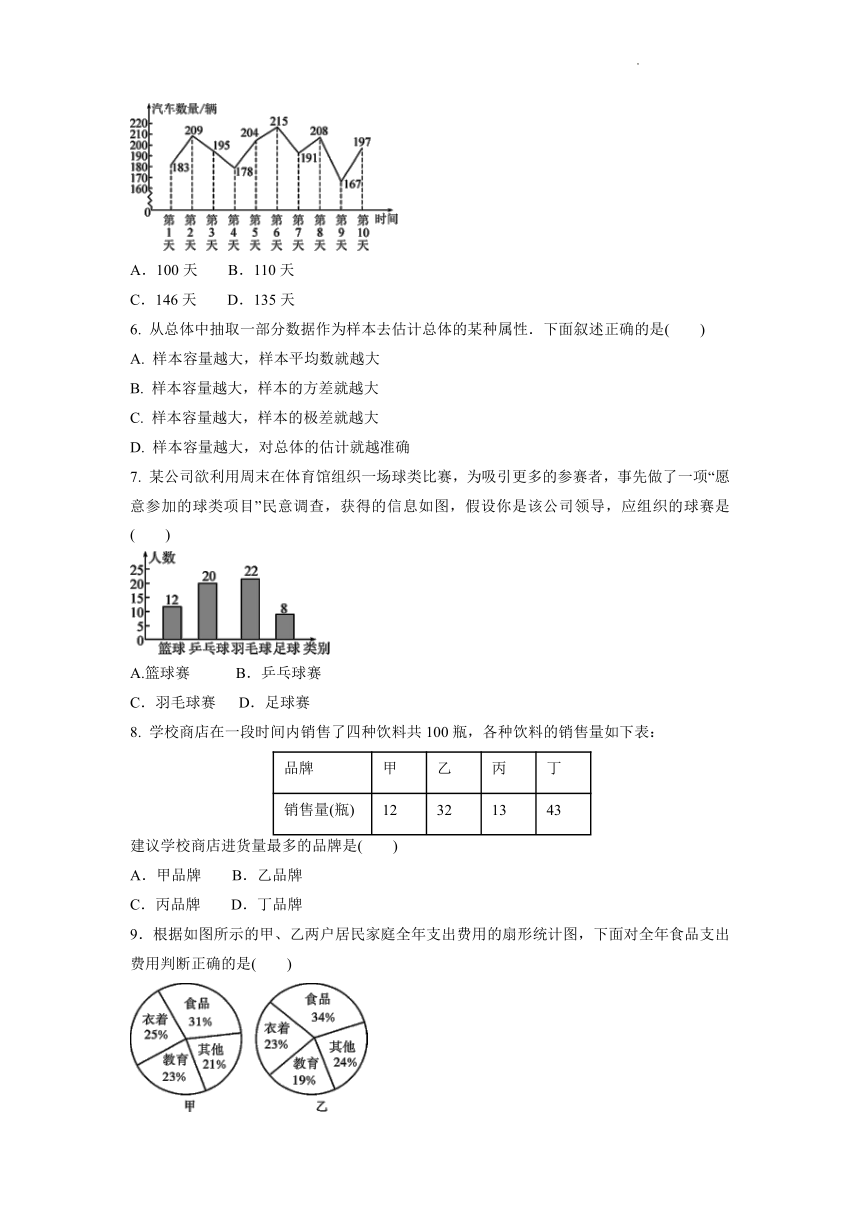
5. 为了解某一路口某一时段的汽车流量,小然同学10天中在同一时段统计通过该路口的汽车数量(单位:辆),将统计结果绘制成如图所示的折线统计图,由此估计一年(365天)该时段通过该路口的汽车数量超过200辆的天数为( )
A.100天 B.110天
C.146天 D.135天
6. 从总体中抽取一部分数据作为样本去估计总体的某种属性.下面叙述正确的是( )
A. 样本容量越大,样本平均数就越大
B. 样本容量越大,样本的方差就越大
C. 样本容量越大,样本的极差就越大
D. 样本容量越大,对总体的估计就越准确
7. 某公司欲利用周末在体育馆组织一场球类比赛,为吸引更多的参赛者,事先做了一项“愿意参加的球类项目”民意调查,获得的信息如图,假设你是该公司领导,应组织的球赛是( )
A.篮球赛 B.乒乓球赛
C.羽毛球赛 D.足球赛
8. 学校商店在一段时间内销售了四种饮料共100瓶,各种饮料的销售量如下表:
品牌 甲 乙 丙 丁
销售量(瓶) 12 32 13 43
建议学校商店进货量最多的品牌是( )
A.甲品牌 B.乙品牌
C.丙品牌 D.丁品牌
9.根据如图所示的甲、乙两户居民家庭全年支出费用的扇形统计图,下面对全年食品支出费用判断正确的是( )
A.甲户比乙户多 B.乙户比甲户多
C.甲、乙两户一样多 D.无法确定哪一户多
10. 如图是某厂连续7年产量增长率(相对于上年的增长率)统计图,仔细观察图形,下列关于该厂7年产量变化的说法正确的是( )
A.产量有增有减 B.产量不断增加
C.产量先下降,后回升 D.以上说法都不对
二.填空题(共6小题,4*6=24)
11. 为“改善城市环境,提高城市品位”,我市加快了“九曲河”旧房拆迁的步伐,为了解被拆迁的1860户家庭对拆迁补偿方案是否满意,市主管部门调查了其中的60户家庭,有52户对方案表示满意,6户表示不满意.在这一抽样调查中,样本容量为 .
12. 小明从编号1~140的总体中抽取了编号为1,3,5,7,9,11,13,15,17,19共10个个体作为一个样本,你认为他这种抽样是否具有随机性?答:________________.
13. 某学校为了增强学生的国防意识,对八年级学生进行了一次国防知识测验.为了解这次测验的成绩状况,从中抽取了50名学生的成绩,将所得数据整理后,画出频数分布直方图如图所示.从图中可知这50名学生的成绩的中位数落在__________范围内.
14. 某学校计划开放A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将结果绘制成如图所示的条形统计图,已知该校学生人数为2 000人,由此估计选修A课程的学生有_________人.
15.甲、乙、丙三人进行射击测试,每人10次射击成绩的平均值都是8.9环,方差分别是s甲2=0.53,s乙2=0.51,s丙2=0.43,则三人中成绩最稳定的是 __
16.某学校计划开放A,B,C,D四门课程供学生选修,规定每名学生必须并且只能选修其中一门.为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图.已知该校学生人数为2 000,由此估计想选修A课程的学生有________名.
三.解答题(共5小题, 56分)
17.(6分) 某校七、八、九三个年级的学生人数比为6∶5∶4,为了了解全校学生参加课外活动的时间,欲从中抽取容量为150样本,现有四种方案.
(1)在九年级学生中用简单随机抽样,抽取150名学生进行调查;
(2)在全校学生中进行简单随机抽样,抽取150名学生进行调查;
(3)分别在三个年级各随机抽取50个样本进行调查;
(4)根据三个年级的人数比,分别在七、八、九年级中随机抽取60人、50人、40人进行调查.
你觉得哪种方案调查的结果会更准确?说说你的理由.
18.(8分) 某校八年级学生会为了解本年级600名学生的睡眠情况,将同学们某天的睡眠时长t(小时)分为A、B、C、D、E(A:9≤t≤24;B:8≤t<9;C:7≤t<8;D:6≤t<7;E:0≤t<6)五个选项,进行了一次问卷调查,随机抽取n名同学的调查问卷并进行了整理,绘制成如下条形统计图,根据统计图提供的信息解答下列问题:
19.(8分) 某中学要开运动会,决定从九年级全部的300名女生中挑选30人,组成一个彩旗方队(要求参加方队的女同学的身高尽可能接近),现在抽测了10名女生的身高,结果如下(单位:厘米):
166 154 151 167 162 158 158 160 162 162
(1)依据样本数据估计,九年级全体女生的平均身高约是多少厘米?
(2)这10名女生的身高的中位数、众数各是多少?
20.(10分) 某生态示范园要对1号、2号、3号、4号四个品牌共500株果树幼苗进行成活实验,从中选出成活率高的品种进行推广,通过实验得知,3号果树幼苗成活率为89.6%,把实验数据绘制成下列两幅统计图.(部分信息未给出)
(1)实验所用的2号果树幼苗的数量是_____株;
(2)请求出3号果树幼苗的成活数,并把图②的统计图补充完整;
(3)你认为应选哪一种品种进行推广?请通过计算说明理由.
21.(12分) 上市公司最近5年的利润情况如下表:
年份 2017 2018 2019 2020 2021
利润/百万元 100 108 110 115 120
(1)在这三个图中,哪个更令人觉得公司的效益上升快?
(2)仔细比较三个图,它们所表示的数据相同吗?
(3)为什么有不同的感觉?
(4)股市有风险,就依股评师的统计图为依据去投资一定合理吗?
22.(12分) 为了了解1200名学生对学校设置的体操、篮球、足球、跑步、舞蹈等课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生.对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图的频数分布直方图和扇形统计图(均不完整).
(1)在这次问卷调查中,一共抽查了 名学生;
(2)估计该校1200名学生中有 人最喜爱篮球活动;
(3)补全频数分布直方图.
参考答案
1-5DDBDC 6-10DCDDB
11.60
12. 不具有随机性
13. 69.5~79.5
14.800
15. 丙
16.800
17.解:(1)只在九年级学生中采取简单随机抽样,不具有代表性
(2)在全校学生中进行简单随机抽样,由于七年级人数最多,所以抽取七年级的概率大,这样不具有代表性
(3)三个年级的学生人数不同,这样抽样不具有代表性
(4)根据三个年级的人数比,也就是在抽样过程中被抽到的概率,用分层抽样的方法从该校七、八、九年级中随机抽取60人、50人、40人进行调查,所以(4)调查的结果会更准确
(1)求n的值;
(2)根据统计结果,估计该年级600名学生中睡眠时长不足7小时的人数.
18. 解:(1)n=12+24+15+6+3=60.
(2)×600=90(人),答:估计该年级600名学生中睡眠时长不足7小时的人数为90.
19. 解:(1)平均数==160所以九年级全体女生平均身高约为160cm.
(2)将这组数据按大小排列:151,154,158,158,160,162,162,162,166,167,位于最中间的是:160和162,故中位数是:(160+162)÷2=161cm;根据162出现次数最多,故众数为162cm.
20. 解:(1)100
(2)500×25%×89.6%=112(株),补图略
(3)1号果树幼苗成活率为×100%=90%;2号果树幼苗成活率为×100%=85%;4号果树幼苗成活率为×100%=93.6%.∵93.6%>90%>89.6%>85%,∴应选择4号品种进行推广
21.解:(1)乙图
(2)相同
(3)三个图中纵轴上同一长度单位表示的意义相同,但单位刻度长短不同,因而图象的倾斜程度不同,给人以不同的感觉
(4)不可完全依据股评师的统计图,应对不同股票的数据在同一坐标中分析会比较合理
22. 解:(1)5÷10%=50(名).故答案为:50;
(2)根据题意得:1200×=480(人);答:该校6000名学生中最喜爱篮球活动的有480人. 故答案为:480;
(3)爱好蓝球小组频数为50﹣5﹣17﹣5﹣3=20 (人),补图如下:
第28章 样本与总体
单元复习训练卷
一、选择题(共10小题,4*10=40)
1. 为了了解某校学生的每日运动量,收集数据正确的是( )
A.调查学校舞蹈队学生每日的运动量
B.调查学校书法小组学生每日的运动量
C.调查学校田径队学生每日的运动量
D.从校七、八、九年级各随机抽取20名学生,调查学生每日的运动量
2. 为了了解某市九年级学生学业水平考试的数学成绩,从中随机抽取1000名学生的数学成绩,下列说法正确的是( )
A.某市九年级学生是总体
B.每一名九年级学生是个体
C.1000名九年级学生是总体的一个样本
D.样本容量是1000
3. 为了解某市参加中考的15000名学生的视力情况,抽取1000名学生的视力进行统计分析,下列判断错误的是( )
A.15000名学生的视力是总体
B.1000名学生是总体的一个样本
C.每名学生的视力是总体的一个个体
D.样本容量为1000
4. 下列调查不适合用简单随机抽样的是( )
A.检查一批罐头的质量是否合格
B.了解一批炮弹的杀伤力
C.调查英文26个字母中使用频率最大的字母
D.了解一个班某次数学考试的平均分
5. 为了解某一路口某一时段的汽车流量,小然同学10天中在同一时段统计通过该路口的汽车数量(单位:辆),将统计结果绘制成如图所示的折线统计图,由此估计一年(365天)该时段通过该路口的汽车数量超过200辆的天数为( )
A.100天 B.110天
C.146天 D.135天
6. 从总体中抽取一部分数据作为样本去估计总体的某种属性.下面叙述正确的是( )
A. 样本容量越大,样本平均数就越大
B. 样本容量越大,样本的方差就越大
C. 样本容量越大,样本的极差就越大
D. 样本容量越大,对总体的估计就越准确
7. 某公司欲利用周末在体育馆组织一场球类比赛,为吸引更多的参赛者,事先做了一项“愿意参加的球类项目”民意调查,获得的信息如图,假设你是该公司领导,应组织的球赛是( )
A.篮球赛 B.乒乓球赛
C.羽毛球赛 D.足球赛
8. 学校商店在一段时间内销售了四种饮料共100瓶,各种饮料的销售量如下表:
品牌 甲 乙 丙 丁
销售量(瓶) 12 32 13 43
建议学校商店进货量最多的品牌是( )
A.甲品牌 B.乙品牌
C.丙品牌 D.丁品牌
9.根据如图所示的甲、乙两户居民家庭全年支出费用的扇形统计图,下面对全年食品支出费用判断正确的是( )
A.甲户比乙户多 B.乙户比甲户多
C.甲、乙两户一样多 D.无法确定哪一户多
10. 如图是某厂连续7年产量增长率(相对于上年的增长率)统计图,仔细观察图形,下列关于该厂7年产量变化的说法正确的是( )
A.产量有增有减 B.产量不断增加
C.产量先下降,后回升 D.以上说法都不对
二.填空题(共6小题,4*6=24)
11. 为“改善城市环境,提高城市品位”,我市加快了“九曲河”旧房拆迁的步伐,为了解被拆迁的1860户家庭对拆迁补偿方案是否满意,市主管部门调查了其中的60户家庭,有52户对方案表示满意,6户表示不满意.在这一抽样调查中,样本容量为 .
12. 小明从编号1~140的总体中抽取了编号为1,3,5,7,9,11,13,15,17,19共10个个体作为一个样本,你认为他这种抽样是否具有随机性?答:________________.
13. 某学校为了增强学生的国防意识,对八年级学生进行了一次国防知识测验.为了解这次测验的成绩状况,从中抽取了50名学生的成绩,将所得数据整理后,画出频数分布直方图如图所示.从图中可知这50名学生的成绩的中位数落在__________范围内.
14. 某学校计划开放A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将结果绘制成如图所示的条形统计图,已知该校学生人数为2 000人,由此估计选修A课程的学生有_________人.
15.甲、乙、丙三人进行射击测试,每人10次射击成绩的平均值都是8.9环,方差分别是s甲2=0.53,s乙2=0.51,s丙2=0.43,则三人中成绩最稳定的是 __
16.某学校计划开放A,B,C,D四门课程供学生选修,规定每名学生必须并且只能选修其中一门.为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图.已知该校学生人数为2 000,由此估计想选修A课程的学生有________名.
三.解答题(共5小题, 56分)
17.(6分) 某校七、八、九三个年级的学生人数比为6∶5∶4,为了了解全校学生参加课外活动的时间,欲从中抽取容量为150样本,现有四种方案.
(1)在九年级学生中用简单随机抽样,抽取150名学生进行调查;
(2)在全校学生中进行简单随机抽样,抽取150名学生进行调查;
(3)分别在三个年级各随机抽取50个样本进行调查;
(4)根据三个年级的人数比,分别在七、八、九年级中随机抽取60人、50人、40人进行调查.
你觉得哪种方案调查的结果会更准确?说说你的理由.
18.(8分) 某校八年级学生会为了解本年级600名学生的睡眠情况,将同学们某天的睡眠时长t(小时)分为A、B、C、D、E(A:9≤t≤24;B:8≤t<9;C:7≤t<8;D:6≤t<7;E:0≤t<6)五个选项,进行了一次问卷调查,随机抽取n名同学的调查问卷并进行了整理,绘制成如下条形统计图,根据统计图提供的信息解答下列问题:
19.(8分) 某中学要开运动会,决定从九年级全部的300名女生中挑选30人,组成一个彩旗方队(要求参加方队的女同学的身高尽可能接近),现在抽测了10名女生的身高,结果如下(单位:厘米):
166 154 151 167 162 158 158 160 162 162
(1)依据样本数据估计,九年级全体女生的平均身高约是多少厘米?
(2)这10名女生的身高的中位数、众数各是多少?
20.(10分) 某生态示范园要对1号、2号、3号、4号四个品牌共500株果树幼苗进行成活实验,从中选出成活率高的品种进行推广,通过实验得知,3号果树幼苗成活率为89.6%,把实验数据绘制成下列两幅统计图.(部分信息未给出)
(1)实验所用的2号果树幼苗的数量是_____株;
(2)请求出3号果树幼苗的成活数,并把图②的统计图补充完整;
(3)你认为应选哪一种品种进行推广?请通过计算说明理由.
21.(12分) 上市公司最近5年的利润情况如下表:
年份 2017 2018 2019 2020 2021
利润/百万元 100 108 110 115 120
(1)在这三个图中,哪个更令人觉得公司的效益上升快?
(2)仔细比较三个图,它们所表示的数据相同吗?
(3)为什么有不同的感觉?
(4)股市有风险,就依股评师的统计图为依据去投资一定合理吗?
22.(12分) 为了了解1200名学生对学校设置的体操、篮球、足球、跑步、舞蹈等课外体育活动项目的喜爱情况,在全校范围内随机抽取了若干名学生.对他们最喜爱的体育项目(每人只选一项)进行了问卷调查,将数据进行了统计并绘制成了如图的频数分布直方图和扇形统计图(均不完整).
(1)在这次问卷调查中,一共抽查了 名学生;
(2)估计该校1200名学生中有 人最喜爱篮球活动;
(3)补全频数分布直方图.
参考答案
1-5DDBDC 6-10DCDDB
11.60
12. 不具有随机性
13. 69.5~79.5
14.800
15. 丙
16.800
17.解:(1)只在九年级学生中采取简单随机抽样,不具有代表性
(2)在全校学生中进行简单随机抽样,由于七年级人数最多,所以抽取七年级的概率大,这样不具有代表性
(3)三个年级的学生人数不同,这样抽样不具有代表性
(4)根据三个年级的人数比,也就是在抽样过程中被抽到的概率,用分层抽样的方法从该校七、八、九年级中随机抽取60人、50人、40人进行调查,所以(4)调查的结果会更准确
(1)求n的值;
(2)根据统计结果,估计该年级600名学生中睡眠时长不足7小时的人数.
18. 解:(1)n=12+24+15+6+3=60.
(2)×600=90(人),答:估计该年级600名学生中睡眠时长不足7小时的人数为90.
19. 解:(1)平均数==160所以九年级全体女生平均身高约为160cm.
(2)将这组数据按大小排列:151,154,158,158,160,162,162,162,166,167,位于最中间的是:160和162,故中位数是:(160+162)÷2=161cm;根据162出现次数最多,故众数为162cm.
20. 解:(1)100
(2)500×25%×89.6%=112(株),补图略
(3)1号果树幼苗成活率为×100%=90%;2号果树幼苗成活率为×100%=85%;4号果树幼苗成活率为×100%=93.6%.∵93.6%>90%>89.6%>85%,∴应选择4号品种进行推广
21.解:(1)乙图
(2)相同
(3)三个图中纵轴上同一长度单位表示的意义相同,但单位刻度长短不同,因而图象的倾斜程度不同,给人以不同的感觉
(4)不可完全依据股评师的统计图,应对不同股票的数据在同一坐标中分析会比较合理
22. 解:(1)5÷10%=50(名).故答案为:50;
(2)根据题意得:1200×=480(人);答:该校6000名学生中最喜爱篮球活动的有480人. 故答案为:480;
(3)爱好蓝球小组频数为50﹣5﹣17﹣5﹣3=20 (人),补图如下:
