【备考2022】泰安市近十年中考数学考点11 圆的综合问题(含答案)
文档属性
| 名称 | 【备考2022】泰安市近十年中考数学考点11 圆的综合问题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 630.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-28 13:49:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
十一、 圆的综合问题
[基础知识]
点与圆,直线与圆的位置关系;
切线的性质与判定;(切线垂直于过切点的半径);(连半径证垂直,作垂直证半径);
三角形的外接圆、内切圆性质;
圆内接四边形的性质。
切线长定理
[中考真题]
(2021)9.(4分)如图,四边形ABCD是⊙O的内接四边形,∠B=90°,∠BCD=120°,AB=2,CD=1,则AD的长为( )
A.2﹣2 B.3﹣ C.4﹣ D.2
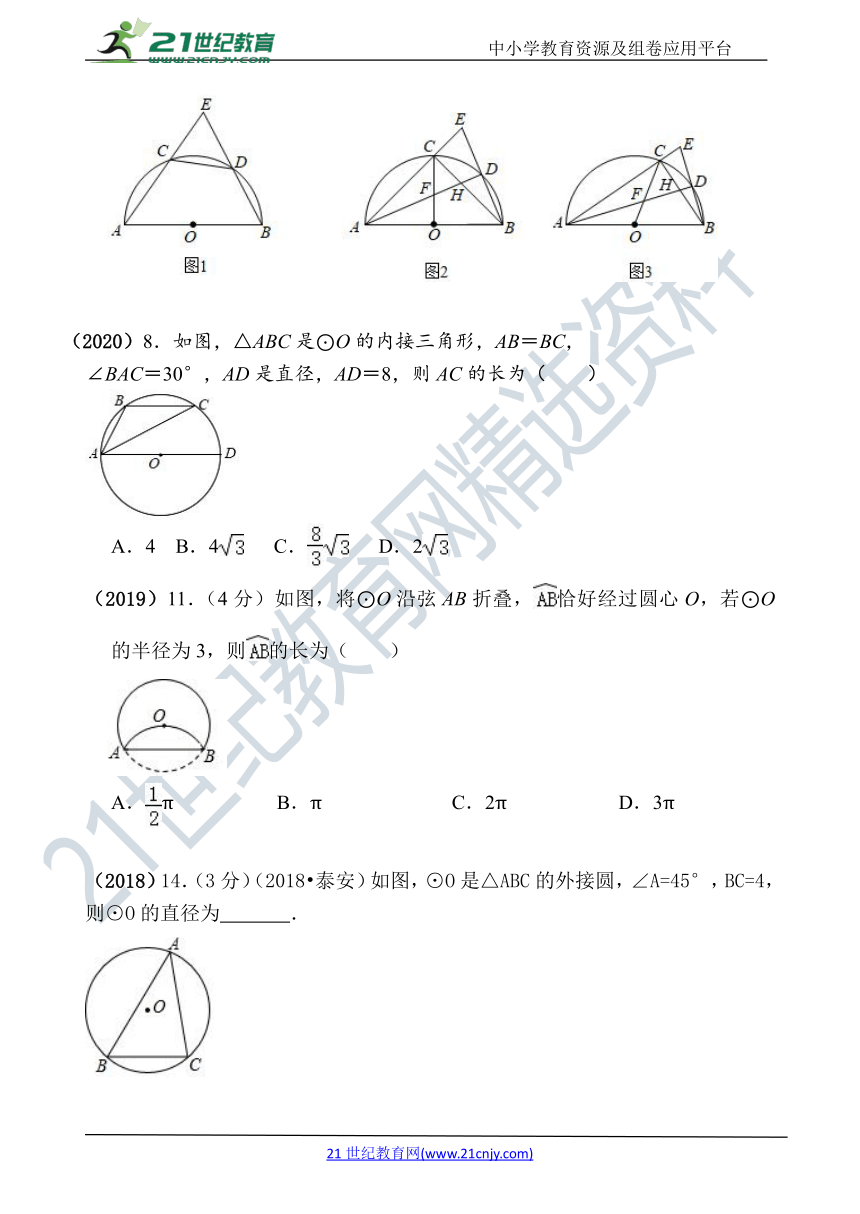
(2021)25.(14分)如图1,O为半圆的圆心,C、D为半圆上的两点,且=.连接AC并延长,与BD的延长线相交于点E.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF AF=FO AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
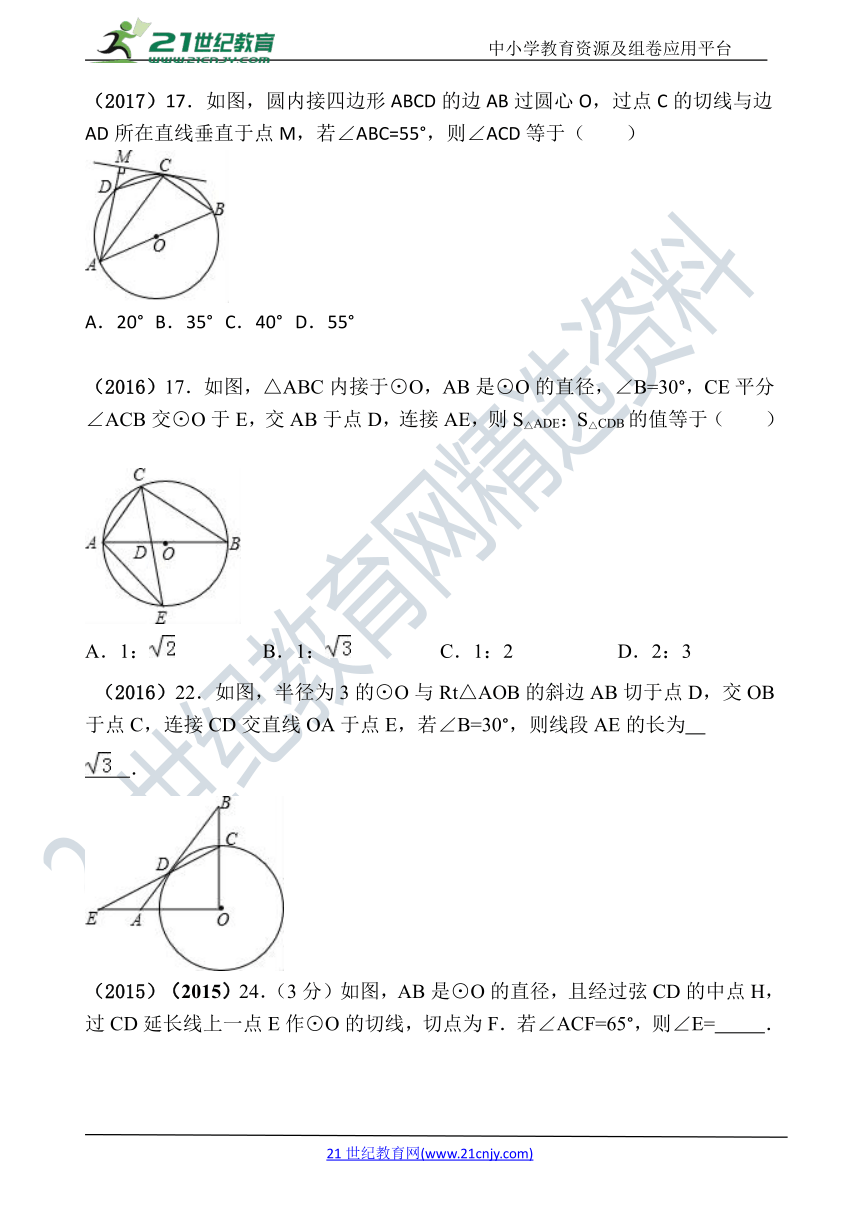
(2020)8.如图,△ABC是⊙O的内接三角形,AB=BC,
∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4 B.4 C. D.2
(2019)11.(4分)如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为( )
A.π B.π C.2π D.3π
(2018)14.(3分)(2018 泰安)如图,⊙O是△ABC的外接圆,∠A=45°,BC=4,则⊙O的直径为 .
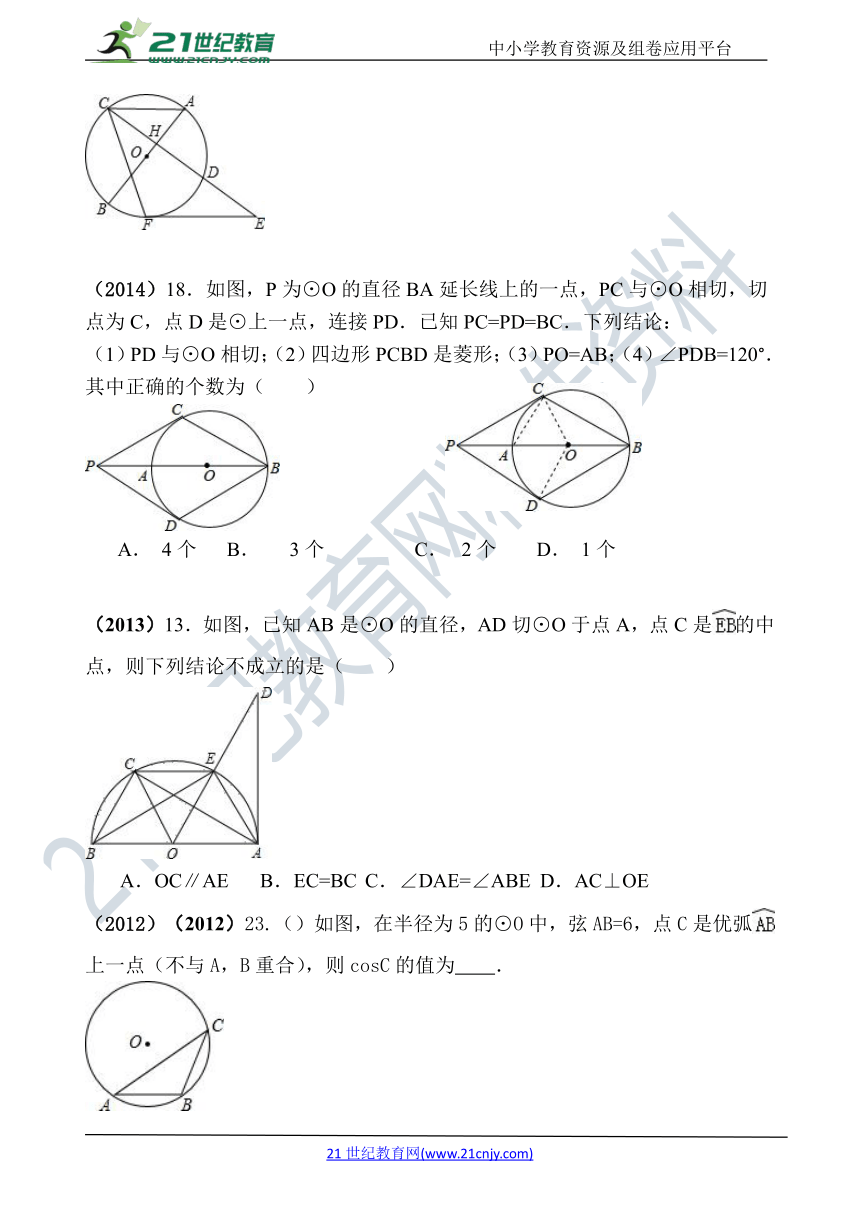
(2017)17.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
(2016)17.如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A.1: B.1: C.1:2 D.2:3
(2016)22.如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为 .
(2015)(2015)24.(3分)如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E= .
( http: / / www.21cnjy.com )
(2014)18.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
4个 B. 3个 C. 2个 D. 1个
(2013)13.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是( )
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
(2012)(2012)23.()如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为 .
[答案解析]
(2021)9.(4分)如图,四边形ABCD是⊙O的内接四边形,∠B=90°,∠BCD=120°,AB=2,CD=1,则AD的长为( )
A.2﹣2 B.3﹣ C.4﹣ D.2
【分析】
【解答】:延长AD、BC交于E,
∵∠BCD=120°,
∴∠A=60°,
∵∠B=90°,
∴∠ADC=90°,∠E=30°,
在Rt△ABE中,AE=2AB=4,
在Rt△CDE中,DE==,
∴AD=AE﹣DE=4﹣,
故选:C.
(2021)25.(14分)如图1,O为半圆的圆心,C、D为半圆上的两点,且=.连接AC并延长,与BD的延长线相交于点E.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF AF=FO AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
【解答】(1)证明:如图1中,连接BC.
∵=,
∴∠DCB=∠DBC,
∵AB是直径,
∴∠ACB=∠BCE=90°,
∴∠E+∠DBC=90°,∠ECD+∠DCB=90°,
∴∠E=∠DCE,
∴DE=DC.
(2)①证明:如图2中,
∵CF=CH,
∴∠CFH=∠CHF,
∵∠AFO=∠CFH,
∴∠AFO=∠CHF,
∵=,
∴∠CAD=∠BAD,
∴△AFO∽△AHC,
∴=,
∴=,
∴CF AF=OF AH.
②解:如图3中,连接CD交BC于G.设OG=x,则DG=2﹣x.
∵=,
∴∠COD=∠BOD,
∵OC=OB,
∴OD⊥BC,CG=BG,
在Rt△OCG和Rt△BGD中,则有22﹣x2=12﹣(2﹣x)2,
∴x=,即OG=,
∵OA=OB,
∴OG是△ABC的中位线,
∴OG=AC,
∴AC=.
(2020)8.如图,△ABC是⊙O的内接三角形,AB=BC,
∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4 B.4 C. D.2
【分析】 连接CD,根据等腰三角形的性质得到∠ACB=∠BAC=30°,根据圆内接四边形的性质得到∠D=180°﹣∠B=60°,求得∠CAD=30°,根据直角三角形的性质即可得到结论.
【解答】: 连接CD,
∵AB=BC,∠BAC=30°,
∴∠ACB=∠BAC=30°,
∴∠B=180°﹣30°﹣30°=120°,
∴∠D=180°﹣∠B=60°,
∴∠CAD=30°,
∵AD是直径,
∴∠ACD=90°,
∵AD=8,
∴CD=AD=4,
∴AC===4,
故选:B.
(2019)11.(4分)如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为( )
A.π B.π C.2π D.3π
【分析】 连接OA、OB,作OC⊥AB于C,根据翻转变换的性质得到OC=OA,根据等腰三角形的性质、三角形内角和定理求出∠AOB,根据弧长公式计算即可.
【解答】解:连接OA、OB,作OC⊥AB于C,
由题意得,OC=OA,
∴∠OAC=30°,
∵OA=OB,
∴∠OBA=∠OAC=30°,
∴∠AOB=120°,
∴的长==2π,
故选:C.
【总结】本题考查的是弧长的计算、直角三角形的性质、翻转变换的性质,掌握弧长公式是解题的关键.
(2018)14.(3分)(2018 泰安)如图,⊙O是△ABC的外接圆,∠A=45°,BC=4,则⊙O的直径为 .
【分析】 连接OB,OC,依据△BOC是等腰直角三角形,即可得到BO=CO=BC cos45°=2,进而得出⊙O的直径为4.
【解答】 :如图,连接OB,OC,
∵∠A=45°,
∴∠BOC=90°,
∴△BOC是等腰直角三角形,
又∵BC=4,
∴BO=CO=BC cos45°=2,
∴⊙O的直径为4,
故答案为:4.
【总结】本题主要考查了三角形的外接圆以及圆周角定理的运用,三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.
(2017)17.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
【分析】 由圆内接四边形的性质求出∠ADC=180°﹣∠ABC=125°,由圆周角定理求出∠ACB=90°,得出∠BAC=35°,由弦切角定理得出∠MCA=∠ABC=55°,由三角形的外角性质得出∠DCM=∠ADC﹣∠AMC=35°,即可求出∠ACD的度数.
【解答】:∵圆内接四边形ABCD的边AB过圆心O,
∴∠ADC+∠ABC=180°,∠ACB=90°,
∴∠ADC=180°﹣∠ABC=125°,∠BAC=90°﹣∠ABC=35°,
∵过点C的切线与边AD所在直线垂直于点M,
∴∠MCA=∠ABC=55°,∠AMC=90°,
∵∠ADC=∠AMC+∠DCM,
∴∠DCM=∠ADC﹣∠AMC=35°,
∴∠ACD=∠MCA﹣∠DCM=55°﹣35°=20°;
故选:A.
(2016)17.如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A.1: B.1: C.1:2 D.2:3
【分析】由AB是⊙O的直径,得到∠ACB=90°,根据已知条件得到,根据三角形的角平分线定理得到=,求出AD=AB,BD=AB,过C作CE⊥AB于E,连接OE,由CE平分∠ACB交⊙O于E,得到OE⊥AB,求出OE=AB,CE=AB,根据三角形的面积公式即可得到结论.
【解答一】∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠B=30°,
∴,
∵CE平分∠ACB交⊙O于E,
∴=,
∴AD=AB,BD=AB,
过C作CE⊥AB于E,连接OE,
∵CE平分∠ACB交⊙O于E,
∴=,
∴OE⊥AB,
∴OE=AB,CE=AB,
∴S△ADE:S△CDB=(ADOE):(BDCE)=():()=2:3.
故选D.
【解答二】设⊙O的半径为x,
∵AB是⊙O的直径,AB=2x,
∴∠ACB=90°,
∵∠B=30°
∴BC=X
∵CE平分∠ACB交⊙O于E,
∴∠ACE=∠ACB=45°
连接OE,
∴∠AOE=2∠ACE=90°,
∴AE=AO=X
∵∠AEC=∠ABC,∠ADE=∠CDB,
∴△ADE∽△CDB
∴S△ADE:S△CDB=(AE:CB)2 =(X:X)2 =2:3.
【总结】本题考查了圆周角定理,三角形的角平分线定理,三角形的面积的计算,直角三角形的性质,相似三角形的性质等基础知识。正确作出辅助线是解题的关键.
(2016) 22.如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为 .
【分析】要求AE的长,只要求出OA和OE的长即可,要求OA的长可以根据∠B=30°和OB的长求得,OE可以根据∠OCE和OC的长求得.
【解答】解:连接OD,如右图所示,
由已知可得,∠BOA=90°,OD=OC=3,∠B=30°,∠ODB=90°,
∴BO=2OD=6,∠BOD=60°,
∴∠ODC=∠OCD=60°,AO=BOtan30°=,
∵∠COE=90°,OC=3,
∴OE=OCtan60°=,
∴AE=OE﹣OA=,
故答案为:.
【总结】本题考查切线的性质,解题的关键是明确题意,找出所求问题需要的条件.
(2015)24.(3分)如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E= .
( http: / / www.21cnjy.com )
【分析】 连接DF,连接AF交CE于G,由AB是⊙O的直径,且经过弦CD的中点H,得到,由于EF是⊙O的切线,推出∠GFE=∠GFD+∠DFE=∠ACF=65°根据外角的性质和圆周角定理得到∠EFG=∠EGF=65°,于是得到结果.2-1-c-n-j-y
【解答一】:连接DF,连接AF交CE于G,
∵AB是⊙O的直径,且经过弦CD的中点H,
∴,
∵EF是⊙O的切线,
∴∠GFE=∠GFD+∠DFE=∠ACF=65°,
∵∠FGD=∠FCD+∠CFA,
∵∠DFE=∠DCF,
∠GFD=∠AFC,
∠EFG=∠EGF=65°,
∴∠E=180°﹣∠EFG﹣∠EGF=50°,
故答案为:50°.
( http: / / www.21cnjy.com )
【解答二】:连接OF,
∵AB是⊙O的直径,且经过弦CD的中点H,
∴AB⊥CD,
∴∠OHD=90°,
∵EF是⊙O的切线,
∴∠OFE=90°,
∵∠ACF=65°
∴∠AOF=130°,
∴∠E=360°﹣∠OFE﹣∠OHD﹣∠AOF=50°,
【总结】本题考查了切线的性质,圆周角定理,垂径定理,正确的作出辅助线是解题的关键.
(2014)18.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
【分析】 (1)利用切线的性质得出∠PCO=90°,进而得出△PCO≌△PDO(SSS),即可得出∠PCO=∠PDO=90°,得出答案即可;
(2)利用(1)所求得出:∠CPB=∠BPD,进而求出△CPB≌△DPB(SAS),即可得出答案;
(3)利用全等三角形的判定得出△PCO≌△BCA(ASA),进而得出CO=PO=AB;
(4)利用四边形PCBD是菱形,∠CPO=30°,则DP=DB,则∠DPB=∠DBP=30°,求出即可.
【解答】:(1)连接CO,DO,
∵PC与⊙O相切,切点为C,∴∠PCO=90°,
在△PCO和△PDO中,,∴△PCO≌△PDO(SSS),∴∠PCO=∠PDO=90°,
∴PD与⊙O相切,故此选项正确;
(2)由(1)得:∠CPB=∠BPD,
在△CPB和△DPB中,,∴△CPB≌△DPB(SAS),
∴BC=BD,∴PC=PD=BC=BD,∴四边形PCBD是菱形,故此选项正确;
(3)连接AC,
∵PC=CB,∴∠CPB=∠CBP,∵AB是⊙O直径,∴∠ACB=90°,
在△PCO和△BCA中,,∴△PCO≌△BCA(ASA),
∴AC=CO,∴AC=CO=AO,∴∠COA=60°,∴∠CPO=30°,
∴CO=PO=AB,∴PO=AB,故此选项正确;
(4)∵四边形PCBD是菱形,∠CPO=30°,
∴DP=DB,则∠DPB=∠DBP=30°,∴∠PDB=120°,故此选项正确;故选:A.
【总结】此题主要考查了切线的判定与性质和全等三角形的判定与性质以及菱形的判定与性质等知识,熟练利用全等三角形的判定与性质是解题关键.
(2013)13.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是( )
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
【分析】 由C为弧EB的中点,利用垂径定理的逆定理得出OC垂直于BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE垂直于BE,即可确定出OC与AE平行,选项A正确;
由C为弧BE中点,即弧BC=弧CE,利用等弧对等弦,得到BC=EC,选项B正确;
由AD为圆的切线,得到AD垂直于OA,进而确定出一对角互余,再由直角三角形ABE中两锐角互余,利用同角的余角相等得到∠DAE=∠ABE,选项C正确;
AC不一定垂直于OE,选项D错误.
【解答】:A.∵点C是的中点,
∴OC⊥BE,
∵AB为圆O的直径,
∴AE⊥BE,
∴OC∥AE,本选项正确;
B.∵=,
∴BC=CE,本选项正确;
C.∵AD为圆O的切线,
∴AD⊥OA,
∴∠DAE+∠EAB=90°,
∵∠EBA+∠EAB=90°,
∴∠DAE=∠EBA,本选项正确;
D.AC不一定垂直于OE,本选项错误,
故选D
【总结】此题考查了切线的性质,圆周角定理,以及圆心角,弧及弦之间的关系,熟练掌握切线的性质是解本题的关键.
(2012)23.()如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为 .
【分析】圆周角定理;勾股定理;垂径定理;锐角三角函数的定义。
【解答】:连接AO并延长到圆上一点D,连接BD,
可得AD为⊙O直径,故∠ABD=90°,
∵半径为5的⊙O中,弦AB=6,则AD=10,
∴BD=,
∵∠D=∠C,
∴cosC=cosD=,
故答案为:.
[解题攻略]
熟练掌握切线的性质,圆心角、圆周角定理,垂径定理,正确的作出辅助线是解题的关键..
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
十一、 圆的综合问题
[基础知识]
点与圆,直线与圆的位置关系;
切线的性质与判定;(切线垂直于过切点的半径);(连半径证垂直,作垂直证半径);
三角形的外接圆、内切圆性质;
圆内接四边形的性质。
切线长定理
[中考真题]
(2021)9.(4分)如图,四边形ABCD是⊙O的内接四边形,∠B=90°,∠BCD=120°,AB=2,CD=1,则AD的长为( )
A.2﹣2 B.3﹣ C.4﹣ D.2
(2021)25.(14分)如图1,O为半圆的圆心,C、D为半圆上的两点,且=.连接AC并延长,与BD的延长线相交于点E.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF AF=FO AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
(2020)8.如图,△ABC是⊙O的内接三角形,AB=BC,
∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4 B.4 C. D.2
(2019)11.(4分)如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为( )
A.π B.π C.2π D.3π
(2018)14.(3分)(2018 泰安)如图,⊙O是△ABC的外接圆,∠A=45°,BC=4,则⊙O的直径为 .
(2017)17.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
(2016)17.如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A.1: B.1: C.1:2 D.2:3
(2016)22.如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为 .
(2015)(2015)24.(3分)如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E= .
( http: / / www.21cnjy.com )
(2014)18.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
4个 B. 3个 C. 2个 D. 1个
(2013)13.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是( )
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
(2012)(2012)23.()如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为 .
[答案解析]
(2021)9.(4分)如图,四边形ABCD是⊙O的内接四边形,∠B=90°,∠BCD=120°,AB=2,CD=1,则AD的长为( )
A.2﹣2 B.3﹣ C.4﹣ D.2
【分析】
【解答】:延长AD、BC交于E,
∵∠BCD=120°,
∴∠A=60°,
∵∠B=90°,
∴∠ADC=90°,∠E=30°,
在Rt△ABE中,AE=2AB=4,
在Rt△CDE中,DE==,
∴AD=AE﹣DE=4﹣,
故选:C.
(2021)25.(14分)如图1,O为半圆的圆心,C、D为半圆上的两点,且=.连接AC并延长,与BD的延长线相交于点E.
(1)求证:CD=ED;
(2)AD与OC,BC分别交于点F,H.
①若CF=CH,如图2,求证:CF AF=FO AH;
②若圆的半径为2,BD=1,如图3,求AC的值.
【解答】(1)证明:如图1中,连接BC.
∵=,
∴∠DCB=∠DBC,
∵AB是直径,
∴∠ACB=∠BCE=90°,
∴∠E+∠DBC=90°,∠ECD+∠DCB=90°,
∴∠E=∠DCE,
∴DE=DC.
(2)①证明:如图2中,
∵CF=CH,
∴∠CFH=∠CHF,
∵∠AFO=∠CFH,
∴∠AFO=∠CHF,
∵=,
∴∠CAD=∠BAD,
∴△AFO∽△AHC,
∴=,
∴=,
∴CF AF=OF AH.
②解:如图3中,连接CD交BC于G.设OG=x,则DG=2﹣x.
∵=,
∴∠COD=∠BOD,
∵OC=OB,
∴OD⊥BC,CG=BG,
在Rt△OCG和Rt△BGD中,则有22﹣x2=12﹣(2﹣x)2,
∴x=,即OG=,
∵OA=OB,
∴OG是△ABC的中位线,
∴OG=AC,
∴AC=.
(2020)8.如图,△ABC是⊙O的内接三角形,AB=BC,
∠BAC=30°,AD是直径,AD=8,则AC的长为( )
A.4 B.4 C. D.2
【分析】 连接CD,根据等腰三角形的性质得到∠ACB=∠BAC=30°,根据圆内接四边形的性质得到∠D=180°﹣∠B=60°,求得∠CAD=30°,根据直角三角形的性质即可得到结论.
【解答】: 连接CD,
∵AB=BC,∠BAC=30°,
∴∠ACB=∠BAC=30°,
∴∠B=180°﹣30°﹣30°=120°,
∴∠D=180°﹣∠B=60°,
∴∠CAD=30°,
∵AD是直径,
∴∠ACD=90°,
∵AD=8,
∴CD=AD=4,
∴AC===4,
故选:B.
(2019)11.(4分)如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为( )
A.π B.π C.2π D.3π
【分析】 连接OA、OB,作OC⊥AB于C,根据翻转变换的性质得到OC=OA,根据等腰三角形的性质、三角形内角和定理求出∠AOB,根据弧长公式计算即可.
【解答】解:连接OA、OB,作OC⊥AB于C,
由题意得,OC=OA,
∴∠OAC=30°,
∵OA=OB,
∴∠OBA=∠OAC=30°,
∴∠AOB=120°,
∴的长==2π,
故选:C.
【总结】本题考查的是弧长的计算、直角三角形的性质、翻转变换的性质,掌握弧长公式是解题的关键.
(2018)14.(3分)(2018 泰安)如图,⊙O是△ABC的外接圆,∠A=45°,BC=4,则⊙O的直径为 .
【分析】 连接OB,OC,依据△BOC是等腰直角三角形,即可得到BO=CO=BC cos45°=2,进而得出⊙O的直径为4.
【解答】 :如图,连接OB,OC,
∵∠A=45°,
∴∠BOC=90°,
∴△BOC是等腰直角三角形,
又∵BC=4,
∴BO=CO=BC cos45°=2,
∴⊙O的直径为4,
故答案为:4.
【总结】本题主要考查了三角形的外接圆以及圆周角定理的运用,三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.
(2017)17.如图,圆内接四边形ABCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
【分析】 由圆内接四边形的性质求出∠ADC=180°﹣∠ABC=125°,由圆周角定理求出∠ACB=90°,得出∠BAC=35°,由弦切角定理得出∠MCA=∠ABC=55°,由三角形的外角性质得出∠DCM=∠ADC﹣∠AMC=35°,即可求出∠ACD的度数.
【解答】:∵圆内接四边形ABCD的边AB过圆心O,
∴∠ADC+∠ABC=180°,∠ACB=90°,
∴∠ADC=180°﹣∠ABC=125°,∠BAC=90°﹣∠ABC=35°,
∵过点C的切线与边AD所在直线垂直于点M,
∴∠MCA=∠ABC=55°,∠AMC=90°,
∵∠ADC=∠AMC+∠DCM,
∴∠DCM=∠ADC﹣∠AMC=35°,
∴∠ACD=∠MCA﹣∠DCM=55°﹣35°=20°;
故选:A.
(2016)17.如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A.1: B.1: C.1:2 D.2:3
【分析】由AB是⊙O的直径,得到∠ACB=90°,根据已知条件得到,根据三角形的角平分线定理得到=,求出AD=AB,BD=AB,过C作CE⊥AB于E,连接OE,由CE平分∠ACB交⊙O于E,得到OE⊥AB,求出OE=AB,CE=AB,根据三角形的面积公式即可得到结论.
【解答一】∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠B=30°,
∴,
∵CE平分∠ACB交⊙O于E,
∴=,
∴AD=AB,BD=AB,
过C作CE⊥AB于E,连接OE,
∵CE平分∠ACB交⊙O于E,
∴=,
∴OE⊥AB,
∴OE=AB,CE=AB,
∴S△ADE:S△CDB=(ADOE):(BDCE)=():()=2:3.
故选D.
【解答二】设⊙O的半径为x,
∵AB是⊙O的直径,AB=2x,
∴∠ACB=90°,
∵∠B=30°
∴BC=X
∵CE平分∠ACB交⊙O于E,
∴∠ACE=∠ACB=45°
连接OE,
∴∠AOE=2∠ACE=90°,
∴AE=AO=X
∵∠AEC=∠ABC,∠ADE=∠CDB,
∴△ADE∽△CDB
∴S△ADE:S△CDB=(AE:CB)2 =(X:X)2 =2:3.
【总结】本题考查了圆周角定理,三角形的角平分线定理,三角形的面积的计算,直角三角形的性质,相似三角形的性质等基础知识。正确作出辅助线是解题的关键.
(2016) 22.如图,半径为3的⊙O与Rt△AOB的斜边AB切于点D,交OB于点C,连接CD交直线OA于点E,若∠B=30°,则线段AE的长为 .
【分析】要求AE的长,只要求出OA和OE的长即可,要求OA的长可以根据∠B=30°和OB的长求得,OE可以根据∠OCE和OC的长求得.
【解答】解:连接OD,如右图所示,
由已知可得,∠BOA=90°,OD=OC=3,∠B=30°,∠ODB=90°,
∴BO=2OD=6,∠BOD=60°,
∴∠ODC=∠OCD=60°,AO=BOtan30°=,
∵∠COE=90°,OC=3,
∴OE=OCtan60°=,
∴AE=OE﹣OA=,
故答案为:.
【总结】本题考查切线的性质,解题的关键是明确题意,找出所求问题需要的条件.
(2015)24.(3分)如图,AB是⊙O的直径,且经过弦CD的中点H,过CD延长线上一点E作⊙O的切线,切点为F.若∠ACF=65°,则∠E= .
( http: / / www.21cnjy.com )
【分析】 连接DF,连接AF交CE于G,由AB是⊙O的直径,且经过弦CD的中点H,得到,由于EF是⊙O的切线,推出∠GFE=∠GFD+∠DFE=∠ACF=65°根据外角的性质和圆周角定理得到∠EFG=∠EGF=65°,于是得到结果.2-1-c-n-j-y
【解答一】:连接DF,连接AF交CE于G,
∵AB是⊙O的直径,且经过弦CD的中点H,
∴,
∵EF是⊙O的切线,
∴∠GFE=∠GFD+∠DFE=∠ACF=65°,
∵∠FGD=∠FCD+∠CFA,
∵∠DFE=∠DCF,
∠GFD=∠AFC,
∠EFG=∠EGF=65°,
∴∠E=180°﹣∠EFG﹣∠EGF=50°,
故答案为:50°.
( http: / / www.21cnjy.com )
【解答二】:连接OF,
∵AB是⊙O的直径,且经过弦CD的中点H,
∴AB⊥CD,
∴∠OHD=90°,
∵EF是⊙O的切线,
∴∠OFE=90°,
∵∠ACF=65°
∴∠AOF=130°,
∴∠E=360°﹣∠OFE﹣∠OHD﹣∠AOF=50°,
【总结】本题考查了切线的性质,圆周角定理,垂径定理,正确的作出辅助线是解题的关键.
(2014)18.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
【分析】 (1)利用切线的性质得出∠PCO=90°,进而得出△PCO≌△PDO(SSS),即可得出∠PCO=∠PDO=90°,得出答案即可;
(2)利用(1)所求得出:∠CPB=∠BPD,进而求出△CPB≌△DPB(SAS),即可得出答案;
(3)利用全等三角形的判定得出△PCO≌△BCA(ASA),进而得出CO=PO=AB;
(4)利用四边形PCBD是菱形,∠CPO=30°,则DP=DB,则∠DPB=∠DBP=30°,求出即可.
【解答】:(1)连接CO,DO,
∵PC与⊙O相切,切点为C,∴∠PCO=90°,
在△PCO和△PDO中,,∴△PCO≌△PDO(SSS),∴∠PCO=∠PDO=90°,
∴PD与⊙O相切,故此选项正确;
(2)由(1)得:∠CPB=∠BPD,
在△CPB和△DPB中,,∴△CPB≌△DPB(SAS),
∴BC=BD,∴PC=PD=BC=BD,∴四边形PCBD是菱形,故此选项正确;
(3)连接AC,
∵PC=CB,∴∠CPB=∠CBP,∵AB是⊙O直径,∴∠ACB=90°,
在△PCO和△BCA中,,∴△PCO≌△BCA(ASA),
∴AC=CO,∴AC=CO=AO,∴∠COA=60°,∴∠CPO=30°,
∴CO=PO=AB,∴PO=AB,故此选项正确;
(4)∵四边形PCBD是菱形,∠CPO=30°,
∴DP=DB,则∠DPB=∠DBP=30°,∴∠PDB=120°,故此选项正确;故选:A.
【总结】此题主要考查了切线的判定与性质和全等三角形的判定与性质以及菱形的判定与性质等知识,熟练利用全等三角形的判定与性质是解题关键.
(2013)13.如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是的中点,则下列结论不成立的是( )
A.OC∥AE B.EC=BC C.∠DAE=∠ABE D.AC⊥OE
【分析】 由C为弧EB的中点,利用垂径定理的逆定理得出OC垂直于BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE垂直于BE,即可确定出OC与AE平行,选项A正确;
由C为弧BE中点,即弧BC=弧CE,利用等弧对等弦,得到BC=EC,选项B正确;
由AD为圆的切线,得到AD垂直于OA,进而确定出一对角互余,再由直角三角形ABE中两锐角互余,利用同角的余角相等得到∠DAE=∠ABE,选项C正确;
AC不一定垂直于OE,选项D错误.
【解答】:A.∵点C是的中点,
∴OC⊥BE,
∵AB为圆O的直径,
∴AE⊥BE,
∴OC∥AE,本选项正确;
B.∵=,
∴BC=CE,本选项正确;
C.∵AD为圆O的切线,
∴AD⊥OA,
∴∠DAE+∠EAB=90°,
∵∠EBA+∠EAB=90°,
∴∠DAE=∠EBA,本选项正确;
D.AC不一定垂直于OE,本选项错误,
故选D
【总结】此题考查了切线的性质,圆周角定理,以及圆心角,弧及弦之间的关系,熟练掌握切线的性质是解本题的关键.
(2012)23.()如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为 .
【分析】圆周角定理;勾股定理;垂径定理;锐角三角函数的定义。
【解答】:连接AO并延长到圆上一点D,连接BD,
可得AD为⊙O直径,故∠ABD=90°,
∵半径为5的⊙O中,弦AB=6,则AD=10,
∴BD=,
∵∠D=∠C,
∴cosC=cosD=,
故答案为:.
[解题攻略]
熟练掌握切线的性质,圆心角、圆周角定理,垂径定理,正确的作出辅助线是解题的关键..
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
