【备考2022】泰安市近十年中考数学 考点12 扇形、圆锥、圆柱等有关计算(含解析)
文档属性
| 名称 | 【备考2022】泰安市近十年中考数学 考点12 扇形、圆锥、圆柱等有关计算(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 363.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-01 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
扇形、圆锥、圆柱等有关计算
[基础知识]
扇形的弧长公式:,扇形面积公式;
圆锥的侧面展开图及其计算;圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长;
求阴影部分面积的方法:不规则图形向规则图形转化,利用图形面积之间的加减关系进行计算;
圆锥的高2+底面圆的半径2=圆锥母线2 。
圆柱的侧面展开图及其计算;
立体图形(正方体、长方体)的展开。
[中考真题]
(2021)16.(3分)若△ABC为直角三角形,AC=BC=4,以BC为直径画半圆如图所示,则阴影部分的面积为 .
(2020) 16.如图,点O是半圆圆心,BE是半圆的直径,点A,D在半圆上,且AD∥BO,∠ABO=60°,AB=8,过点D作DC⊥BE于点C,则阴影部分的面积是 .
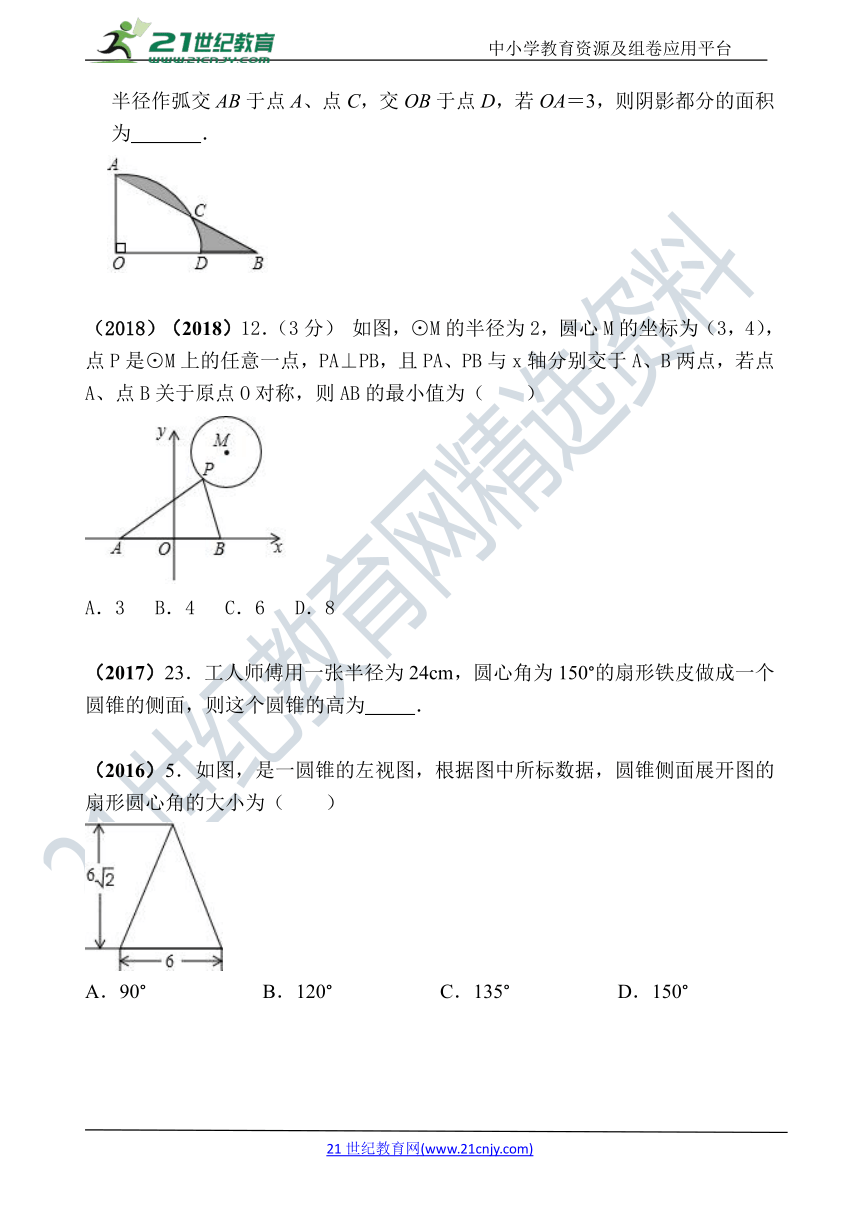
(2019)15.(4分)如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点A、点C,交OB于点D,若OA=3,则阴影都分的面积为 .
(2018)(2018)12.(3分) 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
(2017)23.工人师傅用一张半径为24cm,圆心角为150°的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为 .
(2016)5.如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
A.90° B.120° C.135° D.150°
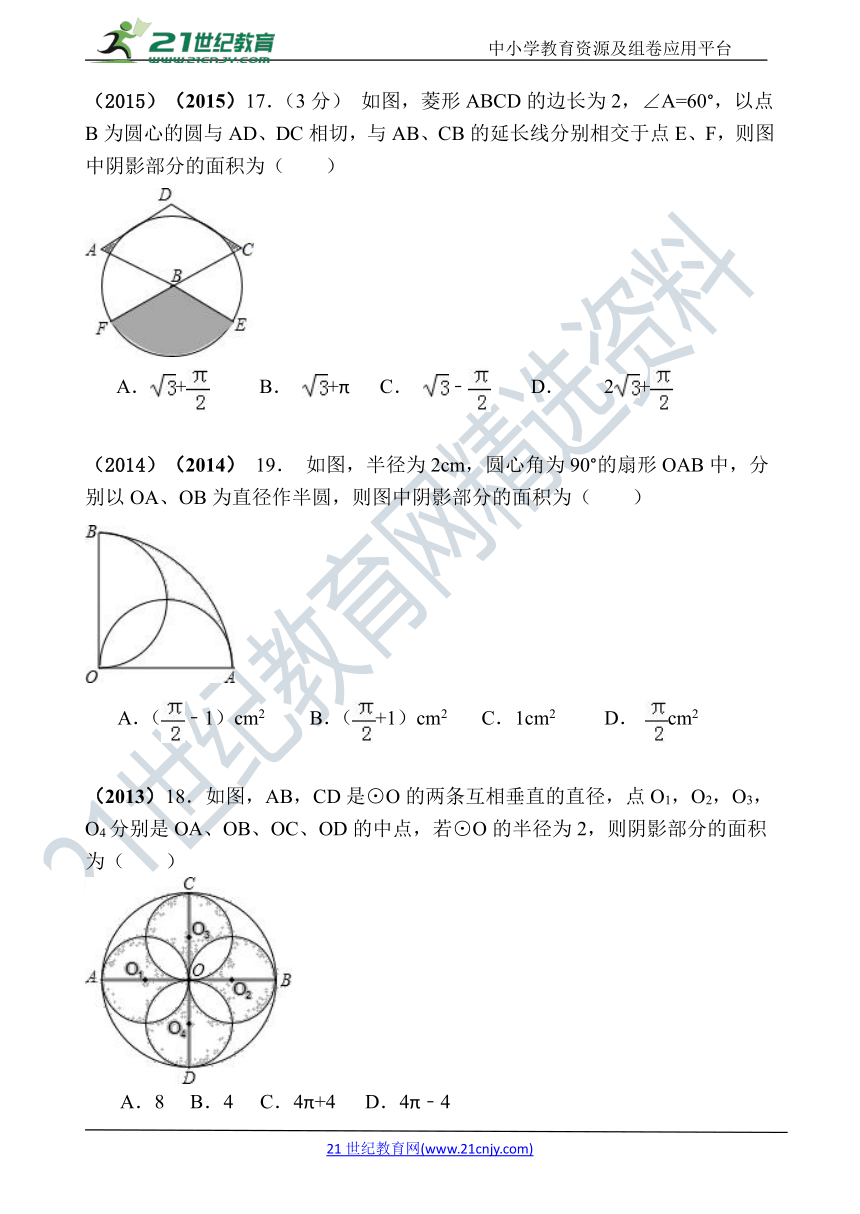
(2015)(2015)17.(3分) 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A.+ B. +π C. ﹣ D. 2+
(2014)(2014) 19. 如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.(﹣1)cm2 B.(+1)cm2 C.1cm2 D. cm2
(2013)18.如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( )
A.8 B.4 C.4π+4 D.4π﹣4
(2012)18. 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则的长为( )
A.π B.2π C.3π D.5π
[答案解析]
(2021)16.(3分)若△ABC为直角三角形,AC=BC=4,以BC为直径画半圆如图所示,则阴影部分的面积为 .
【分析】 连接CD,根据扇形面积公式、三角形面积公式,利用割补法进行求解。
【解答】:连接CD.
∵BC是直径,
∴∠BDC=90°,即CD⊥AB;
又∵△ABC为等腰直角三角形,
∴CD是斜边AB的垂直平分线,
∴CD=BD=AD,
∴=,
∴S弓形BD=S弓形CD,
∴S阴影=SRt△ABC﹣SRt△BCD;
∵△ABC为等腰直角三角形,CD是斜边AB的垂直平分线,
∴SRt△ABC=2SRt△BCD;
又SRt△ABC=×4×4=8,
∴S阴影=4;
故答案为:4.
(2020) 16.如图,点O是半圆圆心,BE是半圆的直径,点A,D在半圆上,且AD∥BO,∠ABO=60°,AB=8,过点D作DC⊥BE于点C,则阴影部分的面积是 .
【分析】 连接OA,易求得圆O的半径为8,扇形的圆心角的度数,然后根据S阴影=S△AOB+S扇形OAD+S扇形ODE﹣S△BCD即可得到结论.
【解答】:连接OA,
∵∠ABO=60°,OA=OB,
∴△AOB是等边三角形,
∵AB=8,∴⊙O的半径为8,
∵AD∥OB,∴∠DAO=∠AOB=60°,
∵OA=OD,∴∠AOD=60°,
∵∠AOB=∠AOD=60°,
∴∠DOE=60°,
∵DC⊥BE于点C,
∴CD=OD=4,OC==4,
∴BC=8+4=12,
S阴影=S△AOB+S扇形OAD+S扇形ODE﹣S△BCD
=×+2×﹣
=﹣8
故答案为﹣8.
(2019)15.(4分)如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点A、点C,交OB于点D,若OA=3,则阴影都分的面积为 .
【分析】连接OC,作CH⊥OB于H,根据直角三角形的性质求出AB,根据勾股定理求出BD,证明△AOC为等边三角形,得到∠AOC=60°,∠COB=30°,根据扇形面积公式、三角形面积公式计算即可.
【解答】:连接OC,作CH⊥OB于H,
∵∠AOB=90°,∠B=30°,
∴∠OAB=60°,AB=2OA=6,
由勾股定理得,OB==3,
∵OA=OC,∠OAB=60°,
∴△AOC为等边三角形,
∴∠AOC=60°,
∴∠COB=30°,
∴CO=CB,CH=OC=,
∴阴影都分的面积=﹣×3×3×+×3×﹣=π,
故答案为:π.
【总结】本题考查的是扇形面积计算、等边三角形的判定和性质,掌握扇形面积公式、三角形的面积公式是解题的关键.
(2018)12.(3分) 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
【分析】由Rt△APB中AB=2OP知要使AB取得最小值,则PO需取得最小值,连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,据此求解可得.
【解答】:∵PA⊥PB,
∴∠APB=90°,
∵AO=BO,
∴AB=2PO,
若要使AB取得最小值,则PO需取得最小值,
连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,
过点M作MQ⊥x轴于点Q,
则OQ=3、MQ=4,
∴OM=5,
又∵MP′=2,
∴OP′=3,
∴AB=2OP′=6,
故选:C.
【总结】本题主要考查点与圆的位置关系,解题的关键是根据直角三角形斜边上的中线等于斜边的一半得出AB取得最小值时点P的位置.
(2017)23.工人师傅用一张半径为24cm,圆心角为150°的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为 .
【分析】 直接利用圆锥的性质求出圆锥的半径,进而利用勾股定理得出圆锥的高.
【解答】解:由题意可得圆锥的母线长为:24cm,
设圆锥底面圆的半径为:r,则2πr=,
解得:r=10,
故这个圆锥的高为: =2(cm).
故答案为:2(cm).
(2016)5.如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
A.90° B.120° C.135° D.150°
【分析】根据圆锥的底面半径得到圆锥的底面周长,也就是圆锥的侧面展开图的弧长,根据勾股定理得到圆锥的母线长,利用弧长公式可求得圆锥的侧面展开图中扇形的圆心角.
【解答】:∵圆锥的底面半径为3,
∴圆锥的底面周长为6π,
∵圆锥的高是6,
∴圆锥的母线长为=9,
设扇形的圆心角为n°,
∴=6π,
解得n=120.
答:圆锥的侧面展开图中扇形的圆心角为120°.
故选B.
【总结】本题考查了圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
(2015)17.(3分) 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A.+ B. +π C. ﹣ D. 2+
【分析】 设AD与圆的切点为G,连接BG,通过解直角三角形求得圆的半径,然后根据扇形的面积公式求得三个扇形的面积,进而就可求得阴影的面积.
【解答】:设AD与圆的切点为G,连接BG,
∴BG⊥AD,
∵∠A=60°,BG⊥AD,
∴∠ABG=30°,
在直角△ABG中,BG=AB=×2=,AG=1,
∴圆B的半径为,
∴S△ABG=×1×=
在菱形ABCD中,∠A=60°,则∠ABC=120°,
∴∠EBF=120°,
∴S阴影=(S△ABG﹣S扇形ABG)+S扇形FBE=2(﹣)+=+.
故选A.
( http: / / www.21cnjy.com )
【总结】此题主要考查了菱形的性质以及切线的性质以及扇形面积等知识,正确利用菱形的性质和切线的性质求出圆的半径是解题关键.
(2014)19. 如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.(﹣1)cm2 B. (+1)cm2 C. 1cm2 D. cm2
【分析】 假设出扇形半径,再表示出半圆面积,以及扇形面积,进而即可表示出两部分P,Q面积相等.连接AB,OD,根据两半圆的直径相等可知∠AOD=∠BOD=45°,故可得出绿色部分的面积=S△AOD,利用阴影部分Q的面积为:S扇形AOB﹣S半圆﹣S绿色,故可得出结论.
【解答】:∵扇形OAB的圆心角为90°,假设扇形半径为2,∴扇形面积为:=π(cm2),半圆面积为:×π×12=(cm2),∴SQ+SM =SM+SP=(cm2),
∴SQ=SP,连接AB,OD,
∵两半圆的直径相等,∴∠AOD=∠BOD=45°,∴S绿色=S△AOD=×2×1=1(cm2),
∴阴影部分Q的面积为:S扇形AOB﹣S半圆﹣S绿色=π﹣﹣1=﹣1(cm2).故选:A.
【总结】此题主要考查了扇形面积求法,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.
(2013)18.如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( )
A.8 B.4 C.4π+4 D.4π﹣4
【分析】首先根据已知得出正方形内空白面积,进而得出扇形COB中两空白面积相等,进而得出阴影部分面积.
【解答】:如图所示:可得正方形EFMN,边长为2,
正方形中两部分阴影面积为:4﹣π,
∴正方形内空白面积为:4﹣2(4﹣π)=2π﹣4,
∵⊙O的半径为2,
∴O1,O2,O3,O4的半径为1,
∴小圆的面积为:π×12=π,
扇形COB的面积为:=π,
∴扇形COB中两空白面积相等,
∴阴影部分的面积为:π×22﹣2(2π﹣4)=8.
故选:A.
【总结】此题主要考查了扇形的面积公式以及正方形面积公式,根据已知得出空白面积是解题关键.
(2012)18. 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则的长为( )
A.π B.2π C.3π D.5π
【分析】切线的性质;弧长的计算。
【解答】:连接OB,
∵AB与⊙O相切于点B,
∴∠ABO=90°,
∵∠ABC=120°,
∴∠OBC=30°,
∵OB=OC,
∴∠OCB=30°,
∴∠BOC=120°,
∴DC的长为
故选B.
[解题攻略]
熟练掌握扇形的弧长和面积公式,知道圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.熟悉圆锥的计算方法是解本类题目的关键.求阴影部分的面积,要注意不规则图形向规则图形转化,和图形面积之间的加减关系。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
扇形、圆锥、圆柱等有关计算
[基础知识]
扇形的弧长公式:,扇形面积公式;
圆锥的侧面展开图及其计算;圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长;
求阴影部分面积的方法:不规则图形向规则图形转化,利用图形面积之间的加减关系进行计算;
圆锥的高2+底面圆的半径2=圆锥母线2 。
圆柱的侧面展开图及其计算;
立体图形(正方体、长方体)的展开。
[中考真题]
(2021)16.(3分)若△ABC为直角三角形,AC=BC=4,以BC为直径画半圆如图所示,则阴影部分的面积为 .
(2020) 16.如图,点O是半圆圆心,BE是半圆的直径,点A,D在半圆上,且AD∥BO,∠ABO=60°,AB=8,过点D作DC⊥BE于点C,则阴影部分的面积是 .
(2019)15.(4分)如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点A、点C,交OB于点D,若OA=3,则阴影都分的面积为 .
(2018)(2018)12.(3分) 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
(2017)23.工人师傅用一张半径为24cm,圆心角为150°的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为 .
(2016)5.如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
A.90° B.120° C.135° D.150°
(2015)(2015)17.(3分) 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A.+ B. +π C. ﹣ D. 2+
(2014)(2014) 19. 如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.(﹣1)cm2 B.(+1)cm2 C.1cm2 D. cm2
(2013)18.如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( )
A.8 B.4 C.4π+4 D.4π﹣4
(2012)18. 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则的长为( )
A.π B.2π C.3π D.5π
[答案解析]
(2021)16.(3分)若△ABC为直角三角形,AC=BC=4,以BC为直径画半圆如图所示,则阴影部分的面积为 .
【分析】 连接CD,根据扇形面积公式、三角形面积公式,利用割补法进行求解。
【解答】:连接CD.
∵BC是直径,
∴∠BDC=90°,即CD⊥AB;
又∵△ABC为等腰直角三角形,
∴CD是斜边AB的垂直平分线,
∴CD=BD=AD,
∴=,
∴S弓形BD=S弓形CD,
∴S阴影=SRt△ABC﹣SRt△BCD;
∵△ABC为等腰直角三角形,CD是斜边AB的垂直平分线,
∴SRt△ABC=2SRt△BCD;
又SRt△ABC=×4×4=8,
∴S阴影=4;
故答案为:4.
(2020) 16.如图,点O是半圆圆心,BE是半圆的直径,点A,D在半圆上,且AD∥BO,∠ABO=60°,AB=8,过点D作DC⊥BE于点C,则阴影部分的面积是 .
【分析】 连接OA,易求得圆O的半径为8,扇形的圆心角的度数,然后根据S阴影=S△AOB+S扇形OAD+S扇形ODE﹣S△BCD即可得到结论.
【解答】:连接OA,
∵∠ABO=60°,OA=OB,
∴△AOB是等边三角形,
∵AB=8,∴⊙O的半径为8,
∵AD∥OB,∴∠DAO=∠AOB=60°,
∵OA=OD,∴∠AOD=60°,
∵∠AOB=∠AOD=60°,
∴∠DOE=60°,
∵DC⊥BE于点C,
∴CD=OD=4,OC==4,
∴BC=8+4=12,
S阴影=S△AOB+S扇形OAD+S扇形ODE﹣S△BCD
=×+2×﹣
=﹣8
故答案为﹣8.
(2019)15.(4分)如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点A、点C,交OB于点D,若OA=3,则阴影都分的面积为 .
【分析】连接OC,作CH⊥OB于H,根据直角三角形的性质求出AB,根据勾股定理求出BD,证明△AOC为等边三角形,得到∠AOC=60°,∠COB=30°,根据扇形面积公式、三角形面积公式计算即可.
【解答】:连接OC,作CH⊥OB于H,
∵∠AOB=90°,∠B=30°,
∴∠OAB=60°,AB=2OA=6,
由勾股定理得,OB==3,
∵OA=OC,∠OAB=60°,
∴△AOC为等边三角形,
∴∠AOC=60°,
∴∠COB=30°,
∴CO=CB,CH=OC=,
∴阴影都分的面积=﹣×3×3×+×3×﹣=π,
故答案为:π.
【总结】本题考查的是扇形面积计算、等边三角形的判定和性质,掌握扇形面积公式、三角形的面积公式是解题的关键.
(2018)12.(3分) 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
A.3 B.4 C.6 D.8
【分析】由Rt△APB中AB=2OP知要使AB取得最小值,则PO需取得最小值,连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,据此求解可得.
【解答】:∵PA⊥PB,
∴∠APB=90°,
∵AO=BO,
∴AB=2PO,
若要使AB取得最小值,则PO需取得最小值,
连接OM,交⊙M于点P′,当点P位于P′位置时,OP′取得最小值,
过点M作MQ⊥x轴于点Q,
则OQ=3、MQ=4,
∴OM=5,
又∵MP′=2,
∴OP′=3,
∴AB=2OP′=6,
故选:C.
【总结】本题主要考查点与圆的位置关系,解题的关键是根据直角三角形斜边上的中线等于斜边的一半得出AB取得最小值时点P的位置.
(2017)23.工人师傅用一张半径为24cm,圆心角为150°的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为 .
【分析】 直接利用圆锥的性质求出圆锥的半径,进而利用勾股定理得出圆锥的高.
【解答】解:由题意可得圆锥的母线长为:24cm,
设圆锥底面圆的半径为:r,则2πr=,
解得:r=10,
故这个圆锥的高为: =2(cm).
故答案为:2(cm).
(2016)5.如图,是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )
A.90° B.120° C.135° D.150°
【分析】根据圆锥的底面半径得到圆锥的底面周长,也就是圆锥的侧面展开图的弧长,根据勾股定理得到圆锥的母线长,利用弧长公式可求得圆锥的侧面展开图中扇形的圆心角.
【解答】:∵圆锥的底面半径为3,
∴圆锥的底面周长为6π,
∵圆锥的高是6,
∴圆锥的母线长为=9,
设扇形的圆心角为n°,
∴=6π,
解得n=120.
答:圆锥的侧面展开图中扇形的圆心角为120°.
故选B.
【总结】本题考查了圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
(2015)17.(3分) 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
( http: / / www.21cnjy.com )
A.+ B. +π C. ﹣ D. 2+
【分析】 设AD与圆的切点为G,连接BG,通过解直角三角形求得圆的半径,然后根据扇形的面积公式求得三个扇形的面积,进而就可求得阴影的面积.
【解答】:设AD与圆的切点为G,连接BG,
∴BG⊥AD,
∵∠A=60°,BG⊥AD,
∴∠ABG=30°,
在直角△ABG中,BG=AB=×2=,AG=1,
∴圆B的半径为,
∴S△ABG=×1×=
在菱形ABCD中,∠A=60°,则∠ABC=120°,
∴∠EBF=120°,
∴S阴影=(S△ABG﹣S扇形ABG)+S扇形FBE=2(﹣)+=+.
故选A.
( http: / / www.21cnjy.com )
【总结】此题主要考查了菱形的性质以及切线的性质以及扇形面积等知识,正确利用菱形的性质和切线的性质求出圆的半径是解题关键.
(2014)19. 如图,半径为2cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为( )
A.(﹣1)cm2 B. (+1)cm2 C. 1cm2 D. cm2
【分析】 假设出扇形半径,再表示出半圆面积,以及扇形面积,进而即可表示出两部分P,Q面积相等.连接AB,OD,根据两半圆的直径相等可知∠AOD=∠BOD=45°,故可得出绿色部分的面积=S△AOD,利用阴影部分Q的面积为:S扇形AOB﹣S半圆﹣S绿色,故可得出结论.
【解答】:∵扇形OAB的圆心角为90°,假设扇形半径为2,∴扇形面积为:=π(cm2),半圆面积为:×π×12=(cm2),∴SQ+SM =SM+SP=(cm2),
∴SQ=SP,连接AB,OD,
∵两半圆的直径相等,∴∠AOD=∠BOD=45°,∴S绿色=S△AOD=×2×1=1(cm2),
∴阴影部分Q的面积为:S扇形AOB﹣S半圆﹣S绿色=π﹣﹣1=﹣1(cm2).故选:A.
【总结】此题主要考查了扇形面积求法,根据题意作出辅助线,构造出等腰直角三角形是解答此题的关键.
(2013)18.如图,AB,CD是⊙O的两条互相垂直的直径,点O1,O2,O3,O4分别是OA、OB、OC、OD的中点,若⊙O的半径为2,则阴影部分的面积为( )
A.8 B.4 C.4π+4 D.4π﹣4
【分析】首先根据已知得出正方形内空白面积,进而得出扇形COB中两空白面积相等,进而得出阴影部分面积.
【解答】:如图所示:可得正方形EFMN,边长为2,
正方形中两部分阴影面积为:4﹣π,
∴正方形内空白面积为:4﹣2(4﹣π)=2π﹣4,
∵⊙O的半径为2,
∴O1,O2,O3,O4的半径为1,
∴小圆的面积为:π×12=π,
扇形COB的面积为:=π,
∴扇形COB中两空白面积相等,
∴阴影部分的面积为:π×22﹣2(2π﹣4)=8.
故选:A.
【总结】此题主要考查了扇形的面积公式以及正方形面积公式,根据已知得出空白面积是解题关键.
(2012)18. 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则的长为( )
A.π B.2π C.3π D.5π
【分析】切线的性质;弧长的计算。
【解答】:连接OB,
∵AB与⊙O相切于点B,
∴∠ABO=90°,
∵∠ABC=120°,
∴∠OBC=30°,
∵OB=OC,
∴∠OCB=30°,
∴∠BOC=120°,
∴DC的长为
故选B.
[解题攻略]
熟练掌握扇形的弧长和面积公式,知道圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.熟悉圆锥的计算方法是解本类题目的关键.求阴影部分的面积,要注意不规则图形向规则图形转化,和图形面积之间的加减关系。
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
